1.4: Polinomios

Última actualización
Guardar como PDF

Page ID: 112008

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

En esta sección los alumnos:

Identificar el grado y coeficiente principal de polinomios.
Sumar y restar polinomios.
Multiplicar polinomios.
Usa FOIL para multiplicar binomios.
Realizar operaciones con polinomia
ls de varias variables.

Earl está construyendo una caseta para perros, cuyo frente tiene la forma de un cuadrado rematado con un triángulo. Habrá una puerta rectangular por la que el perro podrá entrar y salir de la casa. Earl quiere encontrar el área del frente de la caseta del perro para que pueda adquirir la cantidad correcta de pintura. Utilizando las medidas del frente de la casa, mostradas en Figura$\PageIndex{1}$, podemos crear una expresión que combine varios términos variables, permitiéndonos resolver este problema y otros similares.

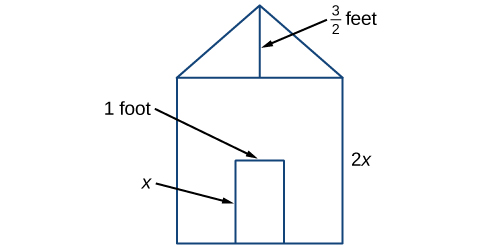
Croquis de una casa formada por un cuadrado y un triángulo basado en la parte superior de la plaza. Se coloca un rectángulo en la parte inferior central del cuadrado para marcar una puerta. La altura de la puerta está etiquetada: x y el ancho de la puerta está etiquetada: 1 pie. El lado del cuadrado está etiquetado: 2x. La altura del triángulo está etiquetada: 3/2 pies. — Figura$\PageIndex{1}$

Primero encuentra el área de la plaza en pies cuadrados.

\[\begin{align*} A &= s^2\\ &= {(2x)}^2\\ &= 4x^2 \end{align*}\]

Después encuentra el área del triángulo en pies cuadrados.

\[\begin{align*} A &= \dfrac{1}{2}bh\\ &= \dfrac{1}{2}(2x)\left (\dfrac{3}{2} \right )\\ &= \dfrac{3}{2}x \end{align*}\]

A continuación encuentra el área de la puerta rectangular en pies cuadrados.

\[\begin{align*} A &= lw\\ &= x\times1\\ &= x \end{align*}\]

El área del frente de la caseta del perro se puede encontrar sumando las áreas del cuadrado y el triángulo, y luego restando el área del rectángulo. Cuando hacemos esto, obtenemos

$4x^2+\dfrac{3}{2}x-x$$ft^2$

$4x^2+\dfrac{1}{2}x$$ft^2$

En esta sección, examinaremos expresiones como esta, que combinan varios términos variables.

Identificación del Grado y Coeficiente Líder de Polinomios

La fórmula que se acaba de encontrar es un ejemplo de un polinomio, que es una suma o diferencia de términos, cada uno de los cuales consiste en una variable elevada a una potencia entera no negativa. Un número multiplicado por una variable elevada a un exponente, tal como$384\pi$, se conoce como coeficiente. Los coeficientes pueden ser positivos, negativos o cero, y pueden ser números enteros, decimales o fracciones. Cada producto$a_ix^i$, tal como$384\pi w$, es un término de un polinomio. Si un término no contiene una variable, se llama constante.

Un polinomio que contiene sólo un término, tal como$5x^4$, se denomina monomio. Un polinomio que contiene dos términos, como$2x−9$, se llama binomio. Un polinomio que contiene tres términos, como$−3x^2+8x−7$, se llama trinomio.

Podemos encontrar el grado de un polinomio identificando la mayor potencia de la variable que ocurre en el polinomio. El término con el grado más alto se llama término principal porque generalmente se escribe primero. El coeficiente del término principal se llama coeficiente principal. Cuando se escribe un polinomio para que los poderes sean descendentes, decimos que está en forma estándar.

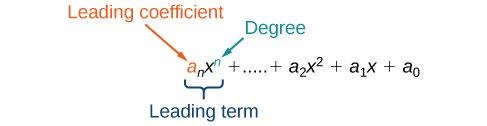
$Se muestra una lectura polinómica: un sub n veces x a la enésima potencia más y así sucesivamente más un sub 2 veces x al cuadrado más un sub uno por x más un bajo cero. La a en el término a sub n se etiqueta: coeficiente principal. La n en el término x a la enésima potencia se etiqueta: grado. Por último, todo el término se etiqueta como: Término principal.$

Polinomios

Un polinomio es una expresión que se puede escribir en la forma

\[a_nx^n+...+a_2x^2+a_1x+a_0\]

Cada número real ai se llama coeficiente. El número$a_0$ que no se multiplica por una variable se llama aconstante. Cada producto$a_ix^i$ es un término de un polinomio. El mayor poder de la variable que ocurre en el polinomio se llama el grado de un polinomio. El término principal es el término con mayor potencia, y su coeficiente se denomina coeficiente principal.

Cómo: Dada una expresión polinómica, identificar el grado y el coeficiente principal.

Encuentra la mayor potencia de x para determinar el grado.
Identificar el término que contiene la mayor potencia de x para encontrar el término principal.
Identificar el coeficiente del término principal.

Ejemplo$\PageIndex{1}$: Identifying the Degree and Leading Coefficient of a Polynomial

Para los siguientes polinomios, identifique el grado, el término principal y el coeficiente principal.

$3+2x^2−4x^3$
$5t^5−2t^3+7t$
$6p−p^3−2$

Solución

El poder más alto de$x$ es$3$, entonces el grado es$3$. El término principal es el término que contiene ese grado,$−4x^3$. El coeficiente principal es el coeficiente de ese término,$−4$.
El poder más alto de$t$ es$5$, entonces el grado es$5$. El término principal es el término que contiene ese grado,$5t^5$. El coeficiente principal es el coeficiente de ese término,$5$.
El poder más alto de$p$ es$3$, entonces el grado es$3$. El término principal es el término que contiene ese grado$−p^3$,, El coeficiente principal es el coeficiente de ese término, −1.

Ejercicio$\PageIndex{1}$

Identificar el grado, término principal y coeficiente principal del polinomio$4x^2−x^6+2x−6$.

Contestar: El grado es$6$, el término principal es$−x^6$, y el coeficiente principal es$−1$.

Sumando y restando polinomios

Podemos sumar y restar polinomios combinando términos similares, que son términos que contienen las mismas variables elevadas a los mismos exponentes. Por ejemplo,$5x^2$ y$−2x^2$ son como términos, y se pueden agregar para obtener$3x^2$, pero$3x$ y no$3x^2$ son como términos, y por lo tanto no se pueden agregar.

Cómo: Dados múltiples polinomios, sumarlos o restarlos para simplificar las expresiones.

Combina términos similares.
Simplificar y escribir en forma estándar.

Ejemplo$\PageIndex{2}$: Adding Polynomials

Encuentra la suma.

$(12x^2+9x−21)+(4x^3+8x^2−5x+20)$

Solución

\[\begin{align*} &4x^3+(12x^2+8x^2)+(9x-5x)+(-21+20)\qquad \text{Combine like terms} \\ &4x^3+20x^2+4x-1\qquad \qquad \qquad \qquad \qquad \qquad \; \; \; \text{Simplify} \end{align*}\]

Análisis

Podemos consultar nuestras respuestas a este tipo de problemas usando una calculadora gráfica. Para verificar, graficar el problema tal como se dio junto con la respuesta simplificada. Las dos gráficas deben ser equivalentes. Asegúrese de usar la misma ventana para comparar las gráficas. El uso de diferentes ventanas puede hacer que las expresiones parezcan equivalentes cuando no lo son.

Ejercicio$\PageIndex{2}$

Encuentra la suma.

$(2x^3+5x^2−x+1)+(2x^2−3x−4)$

Contestar: $2x^3+7x^2−4x−3$

Ejemplo$\PageIndex{3}$: Subtracting Polynomials

Encuentra la diferencia.

$(7x^4−x^2+6x+1)−(5x^3−2x^2+3x+2)$

Solución

$7x^4−5x^3+(−x^2+2x^2)+(6x−3x)+(1−2)$Combinar términos similares

$7x^4−5x^3+x^2+3x−1$Simplificar

Análisis

Tenga en cuenta que encontrar la diferencia entre dos polinomios es lo mismo que agregar lo opuesto del segundo polinomio al primero.

Ejercicio$\PageIndex{3}$

Encuentra la diferencia.

$(−7x^3−7x^2+6x−2)−(4x^3−6x^2−x+7)$

Contestar: $−11x^3−x^2+7x−9$

Multiplicar polinomios

Multiplicar polinomios es un poco más desafiante que sumar y restar polinomios. Debemos utilizar la propiedad distributiva para multiplicar cada término en el primer polinomio por cada término en el segundo polinomio. Luego combinamos términos similares. También podemos usar un atajo llamado método FOIL al multiplicar binomios. Ciertos productos especiales siguen patrones que podemos memorizar y usar en lugar de multiplicar los polinomios a mano cada vez. Veremos una variedad de formas de multiplicar polinomios.

Multiplicación de polinomios mediante la propiedad distributiva

Para multiplicar un número por un polinomio, utilizamos la propiedad distributiva. El número debe ser distribuido a cada término del polinomio. Podemos distribuir el$2$ in$2(x+7)$ para obtener la expresión equivalente$2x+14$. Al multiplicar polinomios, la propiedad distributiva nos permite multiplicar cada término del primer polinomio por cada término del segundo. Luego agregamos los productos y combinamos términos similares para simplificar.

Cómo: Dada la multiplicación de dos polinomios, utilizar la propiedad distributiva para simplificar la expresión.

Multiplique cada término del primer polinomio por cada término del segundo.
Combina términos similares.
Simplificar.

Ejemplo$\PageIndex{4}$: Multiplying Polynomials Using the Distributive Property

Encuentra el producto.

$(2x+1)(3x^2−x+4)$

Solución

\[\begin{align*} &2x(3x^2-x+4)+1(3x^2-x+4)\qquad \text{ Use the distributive property }\\ &(6x^3-2x^2+8x)+(3x^2-x+4)\qquad \text{ Multiply }\\ &6x^3+(-2x^2+3x^2)+(8x-x)+4\qquad \text{ Combine like terms } \\ &6x^3+x^2+7x+4\qquad \text{ Simplify } \end{align*}\]

Análisis

Podemos usar una mesa para hacer un seguimiento de nuestro trabajo, como se muestra en Tabla$\PageIndex{1}$. Escribe un polinomio en la parte superior y el otro por el lado. Para cada cuadro de la tabla, multiplique el término para esa fila por el término para esa columna. Luego agregue todos los términos juntos, combine términos similares y simplifique.

Mesa$\PageIndex{1}$
	$3x^2$	$−x$	$+4$
$2x$	$6x^3$	$−2x^2$	$8x$
$+1$	$3x^2$	$−x$	$4$

Ejercicio$\PageIndex{4}$

Encuentra el producto.

$(3x+2)(x^3−4x^2+7)$

Contestar: $3x^4−10x^3−8x^2+21x+14$

Uso de FOIL para Multiplicar Binomios

A veces se usa un atajo llamado FOIL para encontrar el producto de dos binomios. Se llama FOIL porque multiplicamos los primeros términos, los términos externos, los términos internos, y luego los últimos términos de cada binomio.

$Se están multiplicando dos cantidades entre paréntesis, siendo la primera: a veces x más b y la segunda siendo: c por x más d. Esta expresión es igual a ac por x al cuadrado más tiempos de anuncio x más bc veces x más bd. Los términos ax y cx están etiquetados: Primeros Términos. Los términos ax y d están etiquetados: Términos externos. Los términos b y cx están etiquetados: Términos internos. Los términos b y d están etiquetados: Ultimos Términos.$

El método FOIL surge de la propiedad distributiva. Simplemente estamos multiplicando cada término del primer binomio por cada término del segundo binomio, y luego combinando términos similares.

FOIL para simplificar la expresión

Dados dos binomios, utilice FOIL para simplificar la expresión.

Multiplicar los términos externos de los binomios.
Multiplicar los últimos términos de cada binomio.
Combina términos similares y simplifica.

Ejemplo$\PageIndex{5}$: Using FOIL to Multiply Binomials

Usa FOIL para encontrar el producto.

$(2x−10)(3x+3) \nonumber$

Solución

Encuentra el producto de los primeros términos.

$alt$

Encuentra el producto de los términos externos.

$alt$

Encuentra el producto de los términos internos.

$alt$

Encuentra el producto de los últimos términos.

$alt$

\[\begin{align*} &6x^2+6x-54x-54\qquad \text{Add the products}\\ &6x^2+(6x-54x)-54\qquad \text{Combine like terms} \\ &6x^2-48x-54\qquad \qquad \qquad \text{Simplify} \end{align*}\]

Ejercicio$\PageIndex{5}$

Usa FOIL para encontrar el producto.

$(x+7)(3x−5)$

Contestar: $3x^2+16x−35$

Trinomios Cuadrados Perfectos

Ciertos productos binomiales tienen formas especiales. Cuando un binomio es cuadrado, el resultado se llama trinomio cuadrado perfecto. Podemos encontrar el cuadrado multiplicando el binomio por sí mismo. Sin embargo, hay una forma especial que toma cada uno de estos trinomios cuadrados perfectos, y memorizar la forma hace que cuadrar binomios sea mucho más fácil y rápido. Veamos algunos trinomios cuadrados perfectos para familiarizarnos con la forma.

${(x+5)}^2=x^2+10x+25$

${(x-3)}^2=x^2-6x+9$

${(4x-1)}^2=16x^2-8x+1$

Observe que el primer término de cada trinomio es el cuadrado del primer término del binomio y, de manera similar, el último término de cada trinomio es el cuadrado del último término del binomio. El término medio es el doble del producto de los dos términos. Por último, vemos que el primer signo del trinomio es el mismo que el signo del binomio.

Trinomios Cuadrados Perfectos

Cuando un binomio es cuadrado, el resultado es el primer término al cuadrado agregado para duplicar el producto de ambos términos y el último término al cuadrado.

\[{(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\]

Cómo: Dado un binomio, cuadrarlo usando la fórmula para trinomios cuadrados perfectos.

Cuadrado el primer término del binomio.
Cuadrando el último término del binomio.
Para el término medio del trinomio, duplicar el producto de los dos términos.
Agrega y simplifica.

Ejemplo$\PageIndex{6}$: Expanding Perfect Squares

Ampliar$(3x−8)^2$.

Solución

Comienza por cuadrar el primer trimestre y el último. Para el término medio del trinomio, duplicar el producto de los dos términos.

\[\begin{align*} &{(3x)}^2-2(3x)(8)+{(-8)}^2 \\ &9x^2-48x+64\qquad \qquad \; \; \; \; \text{Simplify} \end{align*}\]

Ejercicio$\PageIndex{6}$

Ampliar${(4x−1)}^2$.

Contestar: $16x^2−8x+1$

Diferencia de Cuadrados

Otro producto especial se llama la diferencia de cuadrados, que ocurre cuando multiplicamos un binomio por otro binomio con los mismos términos pero el signo opuesto. Veamos qué sucede cuando multiplicamos$(x+1)(x−1)$ usando el método FOIL.

\[\begin{align*} (x+1)(x-1) &= x^2-x+x-1\\ &= x^2-1 \end{align*}\]

El término medio cae, resultando en una diferencia de cuadrados. Así como hicimos con los cuadrados perfectos, veamos algunos ejemplos.

$(x+5)(x-5)=x^2-25$

$(x+11)(x-11)=x^2-121$

$(2x+3)(2x-3)=4x^2-9$

Debido a que el signo cambia en el segundo binomio, los términos externo e interno se cancelan entre sí, y nos queda sólo con el cuadrado del primer término menos el cuadrado del último término.

Q&A

¿Existe una forma especial para la suma de cuadrados?

No. La diferencia de cuadrados ocurre porque los signos opuestos de los binomios provocan la desaparición de los términos medios. No hay dos binomios que se multipliquen para igualar una suma de cuadrados.

Diferencia de Cuadrados

Cuando un binomio se multiplica por un binomio con los mismos términos separados por el signo opuesto, el resultado es el cuadrado del primer término menos el cuadrado del último término.

\[(a+b)(a−b)=a^2−b^2\]

Cómo: Dado un binomio multiplicado por un binomio con los mismos términos pero el signo opuesto, encuentra la diferencia de cuadrados.

Cuadrado el primer término de los binomios.
Cuadrando el último término de los binomios.
Restar el cuadrado del último término del cuadrado del primer término.

Ejemplo$\PageIndex{7}$: Multiplying Binomials Resulting in a Difference of Squares

Multiplicar$(9x+4)(9x−4)$.

Solución

Cuadrado el primer término para obtener${(9x)}^2=81x^2$. Cuadrado el último término para obtener$4^2=16$. Restar el cuadrado del último término del cuadrado del primer término para encontrar el producto de$81x^2−16$.

Ejercicio$\PageIndex{7}$

Multiplicar$(2x+7)(2x−7)$.

Contestar: $4x^2−49$

Realización de Operaciones con Polinomios de Varias Variables

Hemos mirado polinomios que contienen una sola variable. Sin embargo, un polinomio puede contener varias variables. Todas las mismas reglas se aplican cuando se trabaja con polinomios que contienen varias variables. Considere un ejemplo:

\[\begin{align*} &(a+2b)(4a-b-c) a(4a-b-c)+2b(4a-b-c)\qquad \text{ Use the distributive property }\\ &4a^2-ab-ac+8ab-2b^2-2bc\qquad \qquad\qquad\qquad\qquad \text{ Multiply }\\ &4a^2+(-ab+8ab)-ac-2b^2-2bc\qquad \qquad\qquad\qquad \; \text{ Combine like terms } \\ &4a^2+7ab-ac-2bc-2b^2\qquad \qquad \qquad \qquad \qquad \qquad\text{ Simplify } \end{align*}\]

Ejemplo$\PageIndex{8}$: Multiplying Polynomials Containing Several Variables

Multiplicar$(x+4)(3x−2y+5)$.

Solución

\[\begin{align*} &x(3x-2y+5)+4(3x-2y+5)\qquad \text{ Use the distributive property }\\ &3x^2-2xy+5x+12x-8y+20\qquad \text{ Multiply }\\ &3x^2-2xy+(5x+12x)-8y+20\qquad \text{ Combine like terms } \\ &3x^2-2xy+17x-8y+20\qquad \qquad\text{ Simplify } \end{align*}\]

Ejercicio$\PageIndex{8}$

Multiplicar$(3x−1)(2x+7y−9)$.

Contestar: $6x^2+21xy−29x−7y+9$

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con polinomios.

Ecuaciones Clave

Trinomio cuadrado perfecto	${(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2$
diferencia de cuadrados	$(a+b)(a−b)=a^2−b^2$

Conceptos clave

Un polinomio es una suma de términos cada uno consistente en una variable elevada a una potencia entera no negativa. El grado es el mayor poder de la variable que ocurre en el polinomio. El término principal es el término que contiene el grado más alto, y el coeficiente principal es el coeficiente de ese término. Ver Ejemplo.
Podemos sumar y restar polinomios combinando términos similares. Ver Ejemplo y Ejemplo.
Para multiplicar polinomios, utilice la propiedad distributiva para multiplicar cada término en el primer polinomio por cada término en el segundo. Luego agrega los productos. Ver Ejemplo.
FOIL (First, Outer, Inner, Last) es un atajo que se puede utilizar para multiplicar binomios. Ver Ejemplo.
Trinomios cuadrados perfectos y diferencia de cuadrados son productos especiales. Ver Ejemplo y Ejemplo.
Siga las mismas reglas para trabajar con polinomios que contengan varias variables. Ver Ejemplo.

	\(3x^2\)	\(−x\)	\(+4\)
\(2x\)	\(6x^3\)	\(−2x^2\)	\(8x\)
\(+1\)	\(3x^2\)	\(−x\)	\(4\)

Search

Text Color

Text Size

Margin Size

Font Type

Polinomios

Cómo: Dada una expresión polinómica, identificar el grado y el coeficiente principal.

Ejemplo\(\PageIndex{1}\): Identifying the Degree and Leading Coefficient of a Polynomial

Ejercicio\(\PageIndex{1}\)

Cómo: Dados múltiples polinomios, sumarlos o restarlos para simplificar las expresiones.

Ejemplo\(\PageIndex{2}\): Adding Polynomials

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\): Subtracting Polynomials

Ejercicio\(\PageIndex{3}\)

Cómo: Dada la multiplicación de dos polinomios, utilizar la propiedad distributiva para simplificar la expresión.

Ejemplo\(\PageIndex{4}\): Multiplying Polynomials Using the Distributive Property

Ejercicio\(\PageIndex{4}\)

FOIL para simplificar la expresión

Ejemplo\(\PageIndex{5}\): Using FOIL to Multiply Binomials

Ejercicio\(\PageIndex{5}\)

Trinomios Cuadrados Perfectos

Cómo: Dado un binomio, cuadrarlo usando la fórmula para trinomios cuadrados perfectos.

Ejemplo\(\PageIndex{6}\): Expanding Perfect Squares

Ejercicio\(\PageIndex{6}\)

Q&A

Diferencia de Cuadrados

Cómo: Dado un binomio multiplicado por un binomio con los mismos términos pero el signo opuesto, encuentra la diferencia de cuadrados.

Ejemplo\(\PageIndex{7}\): Multiplying Binomials Resulting in a Difference of Squares

Ejercicio\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\): Multiplying Polynomials Containing Several Variables

Ejercicio\(\PageIndex{8}\)

Medios

Ecuaciones Clave

Conceptos clave

Trinomio cuadrado perfecto	\({(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\)
diferencia de cuadrados	\((a+b)(a−b)=a^2−b^2\)