5.2: Sumar y restar polinomios
- Page ID
- 112391
Al final de esta sección, podrás:
- Determinar el grado de polinomios
- Sumar y restar polinomios
- Evaluar una función polinómica para un valor dado
- Sumar y restar funciones polinómicas
Antes de comenzar, toma este cuestionario de preparación.
Determinar el grado de polinomios
Hemos aprendido que un término es una constante o producto de una constante y una o más variables. Un monomio es una expresión algebraica con un término. Cuando es de la forma\(ax^m\), donde\(a\) es una constante y\(m\) es un número entero, se le llama monomio en una variable. Algunos ejemplos de monomio en una variable son. Los monomios también pueden tener más de una variable como y\(−4a^2b^3c^2.\)
Un monomio es una expresión algebraica con un término. Un monomio en una variable es un término de la forma\(ax^m\), donde\(a\) es una constante y\(m\) es un número entero.
Un monomio, o dos o más monomios combinados por suma o resta, es un polinomio. Algunos polinomios tienen nombres especiales, basados en el número de términos. Un monomio es un polinomio con exactamente un término. Un binomio tiene exactamente dos términos, y un trinomio tiene exactamente tres términos. No hay nombres especiales para polinomios con más de tres términos.
- polinomio —Un monomio, o dos o más términos algebraicos combinados por suma o resta es un polinomio.
- monomial —Un polinomio con exactamente un término se llama monomio.
- binomio —Un polinomio con exactamente dos términos se llama binomio.
- trinomio —Un polinomio con exactamente tres términos se llama trinomio.
Aquí algunos ejemplos de polinomios.
| Polinomio | \(y+1\) | \(4a^2−7ab+2b^2\) | \(4x^4+x^3+8x^2−9x+1\) | |
|---|---|---|---|---|
| Monomio | \(14\) | \(8y^2\) | \(−9x^3y^5\) | \(−13a^3b^2c\) |
| Binomial | \(a+7ba+7b\) | \(4x^2−y^2\) | \(y^2−16\) | \(3p^3q−9p^2q\) |
| Trinomio | \(x^2−7x+12\) | \(9m^2+2mn−8n^2\) | \(6k^4−k^3+8k\) | \(z^4+3z^2−1\) |
Observe que cada monomio, binomio y trinomio es también un polinomio. Solo son miembros especiales de la “familia” de polinomios y así tienen nombres especiales. Usamos las palabras monomio, binomio y trinomio cuando nos referimos a estos polinomios especiales y simplemente llamamos a todos los polinomios del resto.
El grado de un polinomio y el grado de sus términos están determinados por los exponentes de la variable. Un monomio que no tiene variable, solo una constante, es un caso especial. El grado de una constante es 0.
- El grado de un término es la suma de los exponentes de sus variables.
- El grado de una constante es 0.
- El grado de un polinomio es el grado más alto de todos sus términos.
Veamos cómo funciona esto al observar varios polinomios. Lo llevaremos paso a paso, comenzando por monomios, y luego progresando a polinomios con más términos. Empecemos por mirar un monomio. El monomio\(8ab^2\) tiene dos variables\(a\) y\(b\). Para encontrar el grado necesitamos encontrar la suma de los exponentes. La variable a no tiene un exponente escrito, pero recuerde que eso significa que el exponente es 1. El exponente de\(b\) es 2. La suma de los exponentes, 1+2,1+2, es 3 por lo que el grado es 3.
Aquí hay algunos ejemplos adicionales.
Trabajar con polinomios es más fácil cuando listas los términos en orden descendente de grados. Cuando un polinomio se escribe de esta manera, se dice que está en forma estándar de un polinomio. Acostúmbrese a escribir el término con el grado más alto primero.
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio. Después, encuentra el grado de cada polinomio.
- \(7y2−5y+3\)
- \(−2a^4b^2\)
- \(3x5−4x3−6x2+x−8\)
- \(2y−8xy^3\)
- \(15\)
- Contestar
-
Polinomio Número de términos Tipo Grado de términos Grado de polinomio ⓐ \(7y^2−5y+3\) 3 Trinomio 2, 1, 0 2 ⓑ \(−2a^4b^2−2a^4b^2\) 1 Monomio 4, 2 6 ⓒ \(3x5−4x3−6x2+x−8\) 5 Polinomio 5, 3, 2, 1, 0 5 ⓓ \(2y−8xy^3\) 2 Binomial 1, 4 4 ⓔ \(15\) 1 Monomio 0 0
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio. Después, encuentra el grado de cada polinomio.
- \(−5\)
- \(8y^3−7y^2−y−3\)
- \(−3x^2y−5xy+9xy^3\)
- \(81m^2−4n^2\)
- \(−3x^6y^3z\)
- Contestar a
-
monomio, 0
- Respuesta b
-
polinomio, 3
- Respuesta c
-
trinomio, 3
- Respuesta d
-
binomio, 2
- Respuesta b
-
monomio, 10
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio. Después, encuentra el grado de cada polinomio.
- \(64k^3−8\)
- \(9m^3+4m^2−2\)
- \(56\)
- \(8a^4−7a^3b−6a^2b^2−4ab^3+7b^4\)
- \(-p^4q^3\)
- Contestar
-
ⓐ binomio, 3 ⓑ trinomio, 3 ⓒ monomio, 0 ⓓ polinomio, 4 ⓔ monomio, 7
Sumar y restar polinomios
Hemos aprendido a simplificar expresiones combinando términos similares. Recuerde, los términos similares deben tener las mismas variables con el mismo exponente. Dado que los monomios son términos, sumar y restar monomios es lo mismo que combinar términos similares. Si los monomios son como términos, simplemente los combinamos sumando o restando los coeficientes.
Suma o resta:
- \(25y^2+15y^2\)
- \(16pq^3−(−7pq^3)\).
- Contestar a
-
\( \begin{array} {ll} {} &{25y^2+15y^2} \\ {\text{Combine like terms.}} &{40y^2} \\ \end{array} \nonumber \)
- Respuesta b
-
\( \begin{array} {ll} {} &{16pq^3−(−7pq^3)} \\ {\text{Combine like terms.}} &{23pq^3} \\ \end{array} \nonumber \)
Suma o resta:
- \(12q^2+9q^2\)
- \(8mn^3−(−5mn^3)\).
- Contestar
-
ⓐ\(21q^2\) ⓑ\(13mn^3\)
Suma o resta:
- \(−15c^2+8c^2\)
- \(−15y^2z^3−(−5y^2z^3)\)
- Contestar
-
ⓐ\(−7c^2\) ⓑ\(−10y^2z^3\)
Recuerda que términos similares deben tener las mismas variables con los mismos exponentes.
Simplificar:
- \(a^2+7b^2−6a^2\)
- \(u^2v+5u^2−3v^2\)
- Contestar
-
ⓐ Combina términos similares.
\(a^2+7b^2−6a^2 \;=\; −5a^2+7b^2\)ⓑ No hay términos similares para combinar. En este caso, el polinomio permanece inalterado.
\(u^2v+5u^2−3v^2\)
Agregar:
- \(8y^2+3z^2−3y^2\)
- \(m^2n^2−8m^2+4n^2\)
- Contestar
-
ⓐ\(5y^2+3z^2\)
ⓑ\(m^2n^2−8m^2+4n^2\)
Agregar:
- \(3m^2+n^2−7m^2\)
- \(pq^2−6p−5q^2\)
- Contestar
-
ⓐ\(−4m^2+n^2\)
ⓑ\(pq^2−6p−5q^2\)
Podemos pensar en sumar y restar polinomios como simplemente sumar y restar una serie de monomios. Busque los términos similares, aquellos con las mismas variables y el mismo exponente. La propiedad conmutativa nos permite reorganizar los términos para armar términos similares.
Encuentra la suma:\((7y^2−2y+9)\;+\;(4y^2−8y−7)\).
- Contestar
-
\ (\ begin {align*} &\ text {Identificar términos similares.} & & (\ subrayado {\ subrayado {7y^2}} −\ subrayado {2y} +9) + (\ subrayado {\ subrayado {4y^2}} −\ subrayado {8y} −7)\\ [6pt]
&\ text {Reescribe sin paréntesis,}\\
&\ text {reordenando para obtener los términos similares juntos.} & &\ subrayado {\ subrayado {7y^2+4y^2}} −\ subrayado {2y−8y} +9−7\\ [6pt]
&\ text {Combina términos similares.} & & 11y^2−10y+2\ end {alinear*}\)
Encuentra la suma:\( (7x^2−4x+5)\;+\;(x^2−7x+3)\)
- Contestar
-
\(8x^2−11x+8\)
Encuentra la suma:\((14y^2+6y−4)\;+\;(3y^2+8y+5)\)
- Contestar
-
\(17y^2+14y+1\)
Tenga cuidado con las señales mientras distribuye mientras resta los polinomios en el siguiente ejemplo.
Encuentra la diferencia:\((9w^2−7w+5)\;−\;(2w^2−4)\)
- Contestar
-
\ (\ begin {align*} & & & (9w^2−7w+5)\; −\; (2w^2−4)\\ [6pt]
&\ text {Distribuir e identificar términos similares.} & &\ subrayado {\ subrayado {9w^2}} −\ subrayado {7w} +5-\ subrayado {\ subrayado {2w^2}} +4\\ [6pt]
&\ text {Reorganizar los términos.} & &\ subrayado {\ subrayado {9w^2-2w^2}} −\ subrayado {7w} +5+4\\ [6pt]
&\ text {Combina términos similares.} & & 7w^2−7w+9\ end {alinear*}\)
Encuentra la diferencia:\((8x^2+3x−19)\;−\;(7x^2−14)\)
- Contestar
-
\(x^2+3x−5\)
Encuentra la diferencia:\((9b^2−5b−4)\;−\;(3b^2−5b−7)\)
- Contestar
-
\(6b^2+3\)
Restar\((p^2+10pq−2q^2)\) de\((p^2+q^2)\).
- Contestar
-
\ (\ begin {align*} & & & (p^2+q^2)\; −\; (p^2+10pq−2q^2)\\ [6pt]
&\ text {Distribuir e identificar términos similares.} & &\ subrayado {\ subrayado {p^2}} +\ subrayado {q^2} -\ subrayado {\ subrayado {p^2}} -10pq +\ subrayado {2q^2}\\ [6pt]
&\ text {Reorganizar los términos, juntando términos similares.} & &\ subrayado {\ subrayado {p^2-p^2}} −10pq +\ subrayado {q^2 + 2q^2}\\ [6pt]
&\ text {Combina términos similares.} & & −10pq+3q^2\ end {align*}\)
Restar\((a^2+5ab−6b^2)\) de\((a^2+b^2)\)
- Contestar
-
\(−5ab+7b^2\)
Restar\((m^2−7mn−3n^2)\) de\((m^2+n^2)\).
- Contestar
-
7mn+4n^2
Encuentra la suma:\((u^2−6uv+5v^2)\;+\;(3u^2+2uv)\)
- Contestar
-
\ (\ begin {align*} & & & (u^2−6uv+5v^2)\; +\; (3u^2+2uv)\\ [6pt]
&\ text {Distribuir e identificar términos similares.} &\ subrayado {\ subrayado {u^2}} -\ subrayado {6uv} +5v^2+\ subrayado {\ subrayado {3u^2}} +\ subrayado {2uv}\\ [6pt]
&\ text {Reorganizar los términos para armar términos similares.} & &\ subrayado {\ subrayado {u^2}} +\ subrayado {\ subrayado {3u^2}} -\ subrayado {6uv} +\ subrayado {2uv} +5v^2\\ [6pt]
&\ text {Combina términos similares.} & & 4u^2−4uv+5v^2\ end {alinear*}\)
Encuentra la suma:\((3x^2−4xy+5y^2)\;+\;(2x^2−xy)\)
- Contestar
-
\(5x^2−5xy+5y^2\)
Encuentra la suma:\((2x^2−3xy−2y^2)\;+\;(5x^2−3xy)\)
- Contestar
-
\(7x^2−6xy−2y^2\)
Cuando sumamos y restamos más de dos polinomios, el proceso es el mismo.
Simplificar:\((a^3−a^2b)\;−\;(ab^2+b^3)\;+\;(a^2b+ab^2)\)
- Contestar
-
\ (\ begin {align*} & & & (a^3−a^2b)\; −\; (ab^2+b^3)\; +\; (a^2b+ab^2)\\ [6pt]
&\ text {Distribuir} & & a^3−a^2b − ab^2 - b^3 + a^2b+ab^2\\ [6pt]
&\ text Reorganizar los términos para armar términos similares.} & & a^3−a^2b + a^2b− ab^2 + ab^2 - b^3\\ [6pt]
&\ text {Combina términos similares.} & & a^3−b^3\ end {alinear*}\)
Simplificar:\((x^3−x^2y)\;−\;(xy^2+y^3)\;+\;(x^2y+xy^2)\)
- Contestar
-
\(x^3+y^3\)
Simplificar:\((p^3−p^2q)\;+\;(pq^2+q^3)\;−\;(p^2q+pq^2)\)
- Contestar
-
\(p^3−3p^2q+q^3\)
Evaluar una función polinómica para un valor dado
Una función polinómica es una función definida por un polinomio. Por ejemplo,\(f(x)=x^2+5x+6\) y\(g(x)=3x−4\) son funciones polinómicas, porque\(x^2+5x+6\) y\(3x−4\) son polinomios.
Una función polinómica es una función cuyos valores de rango están definidos por un polinomio.
En Gráficas y Funciones, donde primero introdujimos funciones, aprendimos que evaluar una función significa encontrar el valor de\(f(x)\) para un valor dado de\(x\). Para evaluar una función polinómica, sustituiremos el valor dado por la variable y luego simplificaremos usando el orden de las operaciones.
Para la función\(f(x)=5x^2−8x+4\) encontrar:
- \(f(4)\)
- \(f(−2)\)
- \(f(0)\).
- Contestar
-
ⓐ
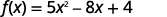
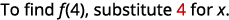
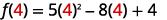
Simplifica los exponentes.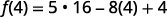 
Multiplicar.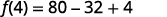 
Simplificar. 
ⓑ
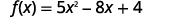
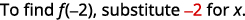
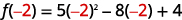
Simplifica los exponentes.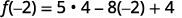 
Multiplicar.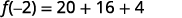 
Simplificar. 
ⓒ
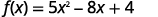
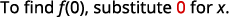
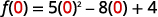
Simplifica los exponentes.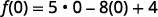 
Multiplicar.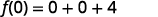 
Para la función\(f(x)=3x^2+2x−15\), encontrar
- \(f(3)\)
- \(f(−5)\)
- \(f(0)\).
- Contestar
-
ⓐ 18 ⓑ 50 ⓒ\(−15\)
Para la función\(g(x)=5x^2−x−4\), encontrar
- \(g(−2)\)
- \(g(−1)\)
- \(g(0)\).
- Contestar
-
ⓐ 20 ⓑ 2 ⓒ\(−4\)
Las funciones polinómicas similares a la del siguiente ejemplo se utilizan en muchos campos para determinar la altura de un objeto en algún momento después de proyectarlo al aire. El polinomio en la siguiente función se usa específicamente para dejar caer algo de 250 pies.
La función polinómica\(h(t)=−16t^2+250\) da la altura de una bola t segundos después de que se cae de un edificio de 250 pies de altura. Encuentra la altura después de\(t=2\) segundos.
- Contestar
-
\( \begin{array} {ll} {} &{h(t)=−16t^2+250} \\ {} &{} \\ {\text{To find }h(2)\text{, substitute }t=2.} &{h(2)=−16(2)^2+250} \\ {\text{Simplify.}} &{h(2)=−16·4+250} \\ {} &{}\\ {\text{Simplify.}} &{h(2)=−64+250} \\ {} &{} \\ {\text{Simplify.}} &{h(2)=186} \\ {} &{\text{After 2 seconds the height of the ball is 186 feet.}} \\ \end{array} \nonumber \)
La función polinómica\(h(t)=−16t^2+150\) da la altura de una piedra t segundos después de que se cae desde un acantilado de 150 pies de altura. Encuentra la altura después de\(t=0\) segundos (la altura inicial del objeto).
- Contestar
-
La altura es\(150\) pies.
La función polinómica\(h(t)=−16t^2+175\) da la altura de una bola t segundos después de que se cae desde un puente de 175 pies de altura. Encuentra la altura después de\(t=3\) segundos.
- Contestar
-
La altura es\(31\) pies.
Sumar y restar funciones polinomiales
Así como se pueden sumar y restar polinomios, también se pueden sumar y restar funciones polinómicas.
Para funciones\(f(x)\) y\(g(x)\),
\[(f+g)(x)=f(x)+g(x)\]
\[(f−g)(x)=f(x)−g(x)\]
Para funciones\(f(x)=3x^2−5x+7\) y\(g(x)=x^2−4x−3\), encuentre:
- \((f+g)(x)\)
- \((f+g)(3)\)
- \((f−g)(x)\)
- \((f−g)(−2)\).
- Contestar
-
ⓐ
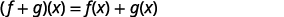
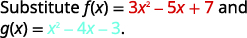
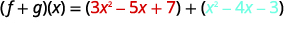
Reescribir sin los paréntesis.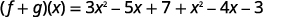 
Poner términos similares juntos.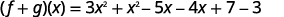 
Combina términos similares.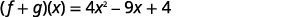 
ⓑ En la parte (a) encontramos\((f+g)(x)\) y ahora se les pide encontrar\((f+g)(3)\).
\( \begin{array} {ll} {} &{(f+g)(x)=4x^2−9x+4} \\ {} &{} \\ {\text{To find }(f+g)\space(3),\text{ substitute }x=3.} &{(f+g)(3)=4(3)^2−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=4·9−9·3+4} \\ {} &{} \\ {} &{(f+g)(3)=36−27+4} \\ \end{array} \nonumber \)
Observe que podríamos haber encontrado\((f+g)(3)\) primero encontrando los valores de\(f(3)\) y\(g(3)\) por separado y luego agregando los resultados.
Encuentra\(f(3)\).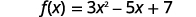 
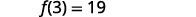
Encuentra\(g(3)\).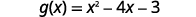 
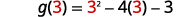
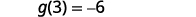
Encuentra\((f+g)(3)\).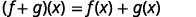 
ⓒ
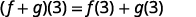
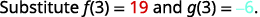
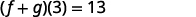
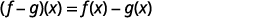
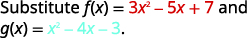
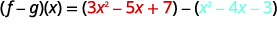
Reescribir sin los paréntesis.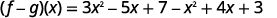 
Poner términos similares juntos.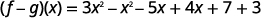 
Combina términos similares.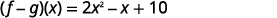 
ⓓ
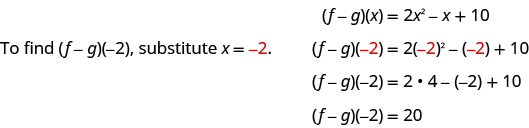
Para funciones\(f(x)=2x^2−4x+3\) y\(g(x)=x^2−2x−6\), encuentra: ⓐ\((f+g)(x)\) ⓑ\((f+g)(3)\) ⓒ\((f−g)(x)\) ⓓ\((f−g)(−2)\).
- Contestar
-
ⓐ\((f+g)(x)=3x^2−6x−3\)
ⓑ\((f+g)(3)=6\)
ⓒ\((f−g)(x)=x^2−2x+9\)
ⓓ\((f−g)(−2)=17\)
Para funciones\(f(x)=5x^2−4x−1\) y\(g(x)=x^2+3x+8\), encuentra ⓐ\((f+g)(x)\) ⓑ\((f+g)(3)\) ⓒ\((f−g)(x)\) ⓓ\((f−g)(−2)\).
- Contestar
-
ⓐ\((f+g)(x)=6x^2−x+7\)
ⓑ\((f+g)(3)=58\)
ⓒ\((f−g)(x)=4x^2−7x−9\)
ⓓ\((f−g)(−2)=21\)
Acceda a este recurso en línea para obtener instrucción adicional y práctica con sumar y restar polinomios.
- Sumando y restando polinomios
Conceptos clave
- Monomio
- Un monomio es una expresión algebraica con un término.
- Un monomio en una variable es un término de la forma axm, axm, donde a es una constante y m es un número entero.
- Polinomios
- Polinomio —Un monomio, o dos o más términos algebraicos combinados por suma o resta es un polinomio.
- monomial —Un polinomio con exactamente un término se llama monomio.
- binomio — Un polinomio con exactamente dos términos se llama binomio.
- trinomio —Un polinomio con exactamente tres términos se llama trinomio.
- Grado de un polinomio
- El grado de un término es la suma de los exponentes de sus variables.
- El grado de una constante es 0.
- El grado de un polinomio es el grado más alto de todos sus términos.
Glosario
- binomio
- Un binomio es un polinomio con exactamente dos términos.
- grado de una constante
- El grado de cualquier constante es 0.
- grado de un polinomio
- El grado de un polinomio es el grado más alto de todos sus términos.
- grado de un término
- El grado de un término es la suma de los exponentes de sus variables.
- monomial
- Un monomio es una expresión algebraica con un término. Un monomio en una variable es un término de la forma axm, axm, donde a es una constante y m es un número entero.
- polinomio
- Un monomio o dos o más monomios combinados por suma o resta es un polinomio.
- forma estándar de un polinomio
- Un polinomio está en forma estándar cuando los términos de un polinomio se escriben en orden descendente de grados.
- trinomio
- Un trinomio es un polinomio con exactamente tres términos.
- función polinómica
- Una función polinómica es una función cuyos valores de rango están definidos por un polinomio.