1.4: Fracciones

Última actualización
Guardar como PDF

Page ID: 108543

Samar ElHitti, Marianna Bonanome, Holly Carley, Thomas Tradler, & Lin Zhou
CUNY New York City College of Technology & NYC College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En nuestra sección anterior identificamos enteros:$0,\pm 1,\pm 2,\pm 3, \ldots .$ A este conjunto, ahora vamos a sumar todas las proporciones de enteros con denominadores distintos de cero, como$\frac{2}{7}, \frac{-11}{17} \ldots$ Llamamos a esto el conjunto de números racionales. Cualquier número racional parece$\frac{p}{q}$ donde$p$ y$q$ son enteros y no$q$ es$0 .$

Así como somos capaces de realizar operaciones aritméticas con enteros también podemos realizar operaciones aritméticas con números racionales (fracciones). Los dos tipos de fracciones que encontraremos se llaman propiamente e impropios:

Las fracciones propias tienen valor menor que$1,$ por ejemplo$\frac{2}{5}$ y$\frac{1}{8} .$ Observe que para estas fracciones el numerador es menor que el denominador.
Las fracciones impropias tienen un valor mayor o igual a$1,$ por ejemplo$\frac{7}{6}$ y$\frac{3}{2} .$ Para estas fracciones el numerador es mayor que el denominador.

Cada valor fraccional puede tener muchas formas diferentes, equivalentes, por ejemplo$1=\frac{2}{2}=\frac{-5}{-5}=\ldots$ Para determinar si dos fracciones son equivalentes podemos usar el principio fundamental de las fracciones.

El principio fundamental de las fracciones

\[\frac{2}{3}=\frac{2 \cdot 4}{3 \cdot 4}=\frac{8}{12}\nonumber\]

Es decir, siempre y cuando multipliques tanto el numerador como el denominador por el mismo número, el valor de la fracción no cambia, y obtienes fracciones equivalentes.

Ejemplo 2.1

Escribe una fracción que sea equivalente a$\frac{3}{5}$.

Solución

Comience con nuestra fracción original$\frac{3}{5}$ y aplique el principio fundamental de fracciones para obtener

\[\frac{3}{5}=\frac{3 \cdot 2}{5 \cdot 2}=\frac{6}{10}\nonumber\]

Ejemplo 2.2

Simplifica la fracción$\frac{15}{35}$.

Solución

Comience con nuestra fracción original y aplique el principio fundamental de fracciones a la inversa para obtener

\[\frac{15}{35}=\frac{3 \cdot 5}{7 \cdot 5}=\frac{3}{7}\nonumber\]

Multiplicar fracciones

Multiplicamos numeradores y denominadores juntos:

\[\frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}\nonumber\]

Ejemplo 2.3

El producto de estas dos fracciones se realiza de la siguiente manera:

\[\frac{14 \cdot 9}{3 \cdot 7}=\frac{2 \cdot 7 \cdot 3 \cdot 3}{3 \cdot 7}=\frac{6}{1}=6\nonumber\]

El recíproco de una fracción

El recíproco de una fracción$\frac{p}{q}$ es la fracción formada cambiando el numerador y el denominador, a saber$\frac{q}{p}$

Ejemplo 2.4

El recíproco de$\frac{3}{5}$ es$\frac{5}{3}$.
El recíproco de$\frac{-2}{7}$ es$\frac{7}{-2}=\frac{-7}{2}=-\frac{7}{2}$.
El recíproco de$\frac{1}{8}$ es$\frac{8}{1}=8$.
El recíproco de$4=\frac{4}{1}$ es$\frac{1}{4}$.

Dividiendo Fracciones

Multiplicamos la primera fracción por el recíproco de la segunda:

\[\frac{a}{b} \div \frac{c}{d}=\frac{a}{b} \cdot \frac{d}{c}=\frac{a \cdot d}{b \cdot c}\nonumber\]

Ejemplo 2.5

El cociente de estas dos fracciones se encuentra de la siguiente manera:

$\frac{8}{3} \div \frac{4}{5}=\frac{8}{3} \cdot \frac{5}{4}=\frac{8 \cdot 5}{3 \cdot 4} =\frac{2 \cdot 4 \cdot 5}{3 \cdot 4}=\frac{10}{3}$

Sumando fracciones (con los mismos denominadores)

\[\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}\nonumber\]

Restar fracciones (con los mismos denominadores)

\[\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}\nonumber\]

Ejemplo 2.6

Agregar$\frac{3}{5}+\frac{1}{5}$

Solución

\[\frac{3}{5}+\frac{1}{5}=\frac{3+1}{5}=\frac{4}{5}\nonumber\]

Sumando o restando fracciones (con denominadores distintos)

Sumar (o restar) fracciones con denominadores diferentes requiere que primero encontremos un denominador común. El LCD o mínimo común denominador es el número más pequeño que ambos denominadores dividen uniformemente. Una vez que reescribimos cada una de nuestras fracciones para que su denominador sea la LCD, podremos sumar o restar fracciones según las propiedades anteriores.

Encontrar la pantalla LCD

Paso 1: Hacer una lista de (suficientes) múltiplos de cada denominador.
Paso 2: Identificar el múltiplo común más bajo. Si no puedes ver uno, entonces tus listas en el Paso 1. necesitan ser expandidas.

Para poder sumar o restar fracciones, necesitamos dar un paso más: Una vez que hayas identificado la LCD, reescribe ambas fracciones (multiplicando tanto el numerador como el denominador por el mismo número apropiado) para obtener la LCD como denominador.

Ejemplo 2.7

Encuentra la pantalla LCD y luego agrega y simplifica$\frac{3}{12}+\frac{5}{8}$.

Solución

Primero encontremos la pantalla LCD siguiendo nuestro procedimiento.

Paso 1. Haga una lista de múltiplos (suficientes):

$8: 8,16,24,32, \ldots$

$12: 12,24,36,48, \ldots$

Paso 2. LCD:$24,8 \cdot 3=24,12 \cdot 2=24$

Paso 3. Reescribe cada fracción usando la pantalla LCD:

\[\frac{3}{12}=\frac{3 \cdot 2}{12 \cdot 2}=\frac{6}{24}\nonumber\]

\[\frac{5}{8}=\frac{5 \cdot 3}{8 \cdot 3}=\frac{15}{24}\nonumber\]

Ahora estamos listos para sumar nuestras fracciones

\[\frac{6}{24}+\frac{15}{24}=\frac{21}{24}\nonumber\]

simplificar los rendimientos

\[\frac{21}{24}=\frac{3 \cdot 7}{3 \cdot 8}=\frac{7}{8}\nonumber\]

Ejemplo 2.8

Encuentra la pantalla LCD y luego resta y simplifica$\frac{1}{9}-\frac{3}{5}$.

Solución

Primero encontremos la pantalla LCD siguiendo nuestro procedimiento.

Paso 1. Haga una lista de múltiplos (suficientes):

$9: 9,18,27,36,45,54,63, \ldots$

$5: 5,10,15,20,25,30,35,40,45,50,55, \ldots$

Paso 2. LCD:$45$

Paso 3. Reescribe cada fracción usando la pantalla LCD:

\[\frac{1}{9}=\frac{1 \cdot 5}{9 \cdot 5}=\frac{5}{45}\nonumber\]

\[\frac{3}{5}=\frac{3 \cdot 9}{5 \cdot 9}=\frac{27}{45}\nonumber\]

Ahora estamos listos para restar nuestras fracciones, pero, primero, reescribimos la resta como suma de lo contrario:

\[\frac{1}{9}-\frac{3}{5}=\frac{1}{9}+\left(-\frac{3}{5}\right)=\frac{5}{45}+\left(-\frac{27}{45}\right)=\frac{5+(-27)}{45}=\frac{-22}{45}\nonumber\]

Escribir una fracción impropia como un número mixto

Divide el numerador por el denominador.
Si hay un resto, escríbelo sobre el denominador.

Ejemplo 2.9

Escribir$\frac{42}{5}$ como un número mixto.

Solución

Comenzamos dividiendo el numerador$42$ por el denominador$5$ para obtener$8,$ con un resto de$2$. Nuestro número mixto es$8 \frac{2}{5}$.

Escribir un número mixto como una fracción impropia

Multiplica el número entero y el denominador luego agrega el numerador. Usa el resultado como tu nuevo numerador.
El denominador sigue siendo el mismo

Ejemplo 2.10

Escribe el número mixto$3 \frac{5}{6}$ como una fracción impropia.

Solución

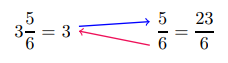$clipboard_e49dfddaac62a80fa44b40165c23ba0dc.png$ Multiplica el denominador por el número entero.
Agrega este resultado al numerador.
Establecer este nuevo numerador 23 sobre el denominador de 6.

Multiplicamos el número entero 3 y el denominador 6 para obtener$18 .$ A continuación, le sumamos a esto el numerador 5 para obtener$23 .$ Este es nuestro nuevo numerador y nuestra fracción impropia se vuelve$\frac{23}{6}$.

Suma y resta de números mixtos

Para sumar (o restar) números mixtos, podemos convertir los números en fracciones impropias, luego sumar (o restar) las fracciones como vimos en este capítulo.

Ejemplo$\PageIndex{1}$

Restar$7-2 \frac{3}{8}$.

Solución

Primero convertimos$2 \frac{3}{8}=\frac{19}{8}$. Luego, reescribimos la operación de resta como suma de opuesto:

\[7-\frac{19}{8}=7+\left(-\frac{19}{8}\right)=\frac{7}{1}+\left(-\frac{19}{8}\right)=\frac{56}{8}+\left(-\frac{19}{8}\right)=\frac{56+(-19)}{8}=\frac{37}{8}=4 \frac{5}{8}\nonumber\]

Además, podemos mantener las fracciones mixtas y la fracción mixta, y sumar (o restar) las partes enteras juntas y las partes de la fracción juntas.

Ejemplo 2.12

Agregar$7 \frac{3}{4}+3 \frac{1}{5}$

Solución

Aquí, agregamos$7+3=10$ y$\frac{3}{4}+\frac{1}{5}=\frac{15}{20}+\frac{4}{20}=\frac{19}{20}$.

Y, nuestra respuesta final es$10 \frac{19}{20}$. Tenga en cuenta que$\frac{19}{20}$ es una fracción propia, entonces, nuestro trabajo está hecho. Pero, si nuestra respuesta terminara con una fracción impropia, hubiéramos tenido que hacer la conversión para escribir la respuesta en forma simplificada.

Multiplicación y división de números mixtos

Tenga cuidado al multiplicar números mixtos. Primero debes convertirlas en fracciones inapropiadas y usar las reglas para multiplicar fracciones para terminar tu problema.

Ejemplo 2.13

Multiplicar$2 \frac{3}{5}$ y$3 \frac{1}{2}$.

Solución

Comience por reescribir cada número mixto como una fracción impropia:$2 \frac{3}{5}=\frac{13}{5}$ y$3 \frac{1}{2}=\frac{7}{2}$. Ahora procedemos multiplicando las fracciones

\[\frac{13}{5} \cdot \frac{7}{2}=\frac{13 \cdot 7}{5 \cdot 2}=\frac{91}{10}\nonumber\]

Ahora podemos escribir el resultado (si lo deseamos) como un número mixto:$9 \frac{1}{10}$.

Ejemplo 2.14

Dividir$\left(1 \frac{4}{5}\right) \div\left(1 \frac{1}{2}\right)$

Solución

Empezamos reescribiendo cada número mixto como una fracción impropia:$1 \frac{4}{5}=\frac{9}{5}$ y$1 \frac{1}{2}=\frac{3}{2} .$ ahora procedemos dividiendo las fracciones

\[\frac{9}{5} \div \frac{3}{2}=\frac{9}{5} \cdot \frac{2}{3}=\frac{9 \cdot 2}{5 \cdot 3}=\frac{3 \cdot 2}{5 \cdot 1}=\frac{6}{5}=1 \frac{1}{5}\nonumber\]

Problema de salida

Evaluar:$\frac{3}{4}-1 \frac{5}{6}$.

Search

Text Color

Text Size

Margin Size

Font Type