1.6: Factorización de polinomios
- Page ID
- 116897
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección los alumnos:
- Factor el mayor factor común de un polinomio.
- Factor a trinomio.
- Factorizar por agrupación.
- Factorizar un trinomio cuadrado perfecto.
- Factorizar una diferencia de cuadrados.
- Factorizar la suma y diferencia de cubos.
- Expresiones factoriales usando exponentes fraccionarios o negativos.
Imagina que estamos tratando de encontrar el área de un césped para que podamos determinar cuánta semilla de pasto comprar. El césped es la porción verde en la Figura\(\PageIndex{1}\).
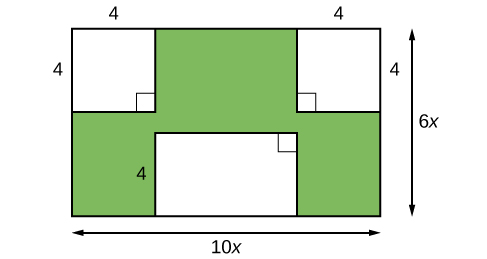
El área de toda la región se puede encontrar usando la fórmula para el área de un rectángulo.
\[\begin{align*} A &= lw\\ &= 10x\times6x\\ &= 60x^2\; units^2 \end{align*}\]
Las áreas de las porciones que no requieren semilla de pasto deben restarse del área de toda la región. Las dos regiones cuadradas tienen cada una un área de\(A =s^2=4^2= 16\; units^2\). La otra región rectangular tiene un lado de longitud\(10x−8\) y un lado de longitud\(4\), dando un área de
\[A =lw=4(10x−8)=40x−32\; \text{units}^2. \nonumber\]
Por lo que la región que debe restarse tiene una superficie de
\[2(16)+40x−32= 40x\; \text{units}^2. \nonumber\]
El área de la región que requiere semilla de pasto se encuentra restando\(60x^2−40x\; \text{units}^2\). Esta área también se puede expresar en forma factorizada como\(20x (3x−2)\; \text{units}^2\). Podemos confirmar que se trata de una expresión equivalente multiplicando.
Muchas expresiones polinómicas se pueden escribir en formas más simples mediante factorización. En esta sección, veremos una variedad de métodos que se pueden utilizar para factorizar expresiones polinómicas.
Factorizar el mayor factor común de un polinomio
Cuando estudiamos fracciones, aprendemos que el mayor factor común (GCF) de dos números es el mayor número que divide uniformemente en ambos números. Por ejemplo,\(4\) es el GCF de\(16\) y\(20\) porque es el mayor número el que se divide uniformemente en ambos\(16\) y\(20\) El GCF de polinomios funciona de la misma manera:\(4x\) es el GCF de\(16x\) y\(20x^2\) porque es el polinomio más grande el que divide uniformemente en ambos\(16x\) y\(20x^2\).
Al factorizar una expresión polinómica, nuestro primer paso debe ser verificar un GCF. Busque el GCF de los coeficientes, y luego busque el GCF de las variables.
El mayor factor común (GCF) de los polinomios es el polinomio más grande que se divide uniformemente en los polinomios.
- Identificar el GCF de los coeficientes.
- Identificar el GCF de las variables.
- Combinar para encontrar el GCF de la expresión.
- Determinar por qué se necesita multiplicar el GCF para obtener cada término en la expresión.
- Escribe la expresión factorizada como producto del GCF y la suma de los términos por los que necesitamos multiplicar.
Factor\(6x^3y^3 +45x^2y^2+21xy\).
Solución
Primero, encontrar el GCF de la expresión. El GCF de\(6\),\(45\), y\(21\) es\(3\). El GCF de\(x^3\),\(x^2\), y\(x\) es\(x\). (Tenga en cuenta que el GCF de un conjunto de expresiones en la forma siempre\(x^n\) será el exponente del grado más bajo). Y el GCF de\(y^3\),\(y^2\), y\(y\) es\(y\). Combínalos para encontrar el GCF del polinomio,\(3xy\).
A continuación, determinar por qué se necesita multiplicar el GCF para obtener cada término del polinomio. Nos encontramos con que
- \(3xy(2x^2y^2)=6x^3y^3\),
- \(3xy(15xy)=45x^2y^2\), y
- \(3xy(7)=21xy\).
Por último, escribir la expresión factorizada como producto del GCF y la suma de los términos por los que necesitábamos multiplicar.
\[(3xy)(2x^2y^2+15xy+7) \nonumber\]
Análisis
Después de factorizar, podemos verificar nuestro trabajo multiplicando. Utilice la propiedad distributiva para confirmar que
\[(3xy)(2x^2y^2+15xy+7)=6x^3y^3+45x^2y^2+21xy \nonumber\]
Factor\(x(b^2−a)+6(b^2−a)\) al sacar el GCF.
- Responder
-
\((b^2−a)(x+6)\)
Factorización de un Trinomio con Coeficiente Líder 1
Aunque siempre debemos comenzar por buscar un GCF, sacar el GCF no es la única manera en que se pueden factorizar expresiones polinómicas. El polinomio\(x^2+5x+6\) tiene un GCF de\(1\), pero puede escribirse como el producto de los factores\((x+2)\) y\((x+3)\).
Los trinomios de la forma se\(x^2+bx+c\) pueden factorizar encontrando dos números con un producto de\(c\) y una suma de\(b\). El trinomio\(x^2+10x+16\), por ejemplo, se puede factorizar usando los números\(2\) y\(8\) porque el producto de esos números es\(16\) y su suma es\(10\). El trinomio puede ser reescrito como producto de\((x+2)\) y\((x+8)\).
Un trinomio de la forma\(x^2+bx+c\) puede escribirse en forma factorizada como\((x+p)(x+q)\) dónde\(pq=c\) y\(p+q=b\).
No. Algunos polinomios no pueden ser factorizados. Se dice que estos polinomios son primos.
- Enumerar factores de\(c\).
- Encontrar\(p\) y\(q\), un par de factores de\(c\) con una suma de\(b\).
- Escribe la expresión factorizada\((x+p)(x+q)\).
Factor\(x^2+2x−15\).
Solución
Tenemos un trinomio con coeficiente principal\(1\),\(b=2\), y\(c=−15\). Necesitamos encontrar dos números con un producto de\(−15\) y una suma de\(2\). En Tabla\(\PageIndex{1}\), enumeramos factores hasta que encontremos un par con la suma deseada.
| Factores de −15 | Suma de factores |
|---|---|
| 1, −15 | −14 |
| −1,15 | 14 |
| 3, −5 | −2 |
| −3,5 |
Ahora que hemos identificado\(p\) y\(q\) como\(−3\) y\(5\), escribir la forma factorizada como\((x−3)(x+5)\).
Análisis
Podemos verificar nuestro trabajo multiplicando. Usa FOIL para confirmarlo\((x−3)(x+5)=x^2+2x−15\).
No. La multiplicación es conmutativa, por lo que el orden de los factores no importa.
Factor\(x^2−7x+6\).
- Responder
-
\((x−6)(x−1)\)
Factorización por Agrupación
Trinomios con coeficientes iniciales distintos a los que\(1\) son ligeramente más complicados de factorizar. Para estos trinomios, podemos factorizar agrupando dividiendo el término x en la suma de dos términos, factorizando cada porción de la expresión por separado, y luego factorizando el GCF de toda la expresión. El trinomio\(2x^2+5x+3\) puede ser reescrito como\((2x+3)(x+1)\) usando este proceso. Comenzamos reescribiendo la expresión original como\(2x^2+2x+3x+3\) y luego factorizamos cada porción de la expresión para obtener\(2x(x+1)+3(x+1)\). Luego sacamos el GCF de\((x+1)\) para encontrar la expresión factorizada.
Para factorizar un trinomio en la forma\(ax^2+bx+c\) agrupando, encontramos dos números con un producto de\(ac\) y una suma de\(b\). Usamos estos números para dividir el\(x\) término en la suma de dos términos y factorizar cada porción de la expresión por separado, luego factorizar el GCF de toda la expresión.
- Enumerar factores de\(ac\).
- Encontrar\(p\) y\(q\), un par de factores de\(ac\) con una suma de\(b\).
- Reescribir la expresión original como\(ax^2+px+qx+c\).
- Saque el GCF de\(ax^2+px\).
- Saque el GCF de\(qx+c\).
- Factorizar el GCF de la expresión.
Factorizar\(5x^2+7x−6\) por agrupación.
Solución
Tenemos un trinomio con\(a=5\),\(b=7\), y\(c=−6\). Primero, determinar\(ac=−30\). Necesitamos encontrar dos números con un producto de\(−30\) y una suma de\(7\). En la siguiente tabla, enumeramos los factores hasta que encontremos un par con la suma deseada.
| Factores de −30 | Suma de factores |
|---|---|
| 1, −30 | −29 |
| −1,30 | 29 |
| 2, −15 | −13 |
| −2,15 | 13 |
| 3, −10 | −7 |
| −3,10 | 7 |
Entonces\(p=−3\) y\(q=10\).
\(5x^2−3x+10x−6\)Reescribir la expresión original como\(ax^2+px+qx+c\).
\(x(5x−3)+2(5x−3)\)Factorizar el GCF de cada parte
\((5x−3)(x+2)\)Factorizar el GCF de la expresión.
Análisis
Podemos verificar nuestro trabajo multiplicando. Usa FOIL para confirmarlo\((5x−3)(x+2)=5x^2+7x−6\).
Factor:
- \(2x^2+9x+9\)
- \(6x^2+x−1\)
- Contestar a
-
\((2x+3)(x+3)\)
- Respuesta b
-
\((3x-1)(2x+1)\)
Factorizar un Trinomio Cuadrado Perfecto
Un trinomio cuadrado perfecto es un trinomio que puede escribirse como el cuadrado de un binomio. Recordemos que cuando se cuadra un binomio, el resultado es el cuadrado del primer término sumado al doble del producto de los dos términos y el cuadrado del último término.
\[a^2+2ab+b^2={(a+b)}^2\]
y
\[a^2-2ab+b^2={(a-b)}^2\]
Podemos usar esta ecuación para factorizar cualquier trinomio cuadrado perfecto.
Un trinomio cuadrado perfecto se puede escribir como el cuadrado de un binomio:
\[a^2+2ab+b^2=(a+b)^2\]
- Confirmar que el primer y último término son cuadrados perfectos.
- Confirmar que el término medio es el doble del producto de\(ab\).
- Escribe la forma factorizada como\({(a+b)}^2\).
Factor\(25x^2+20x+4\).
Solución
Observe que\(25x^2\) y\(4\) son cuadrados perfectos porque\(25x^2={(5x)}^2\) y\(4=2^2\). Después revisa para ver si el término medio es el doble del producto de\(5x\) y\(2\). El término medio es, efectivamente, el doble del producto:\(2(5x)(2)=20x\). Por lo tanto, el trinomio es un trinomio cuadrado perfecto y puede escribirse como\({(5x+2)}^2\).
Factor\(49x^2−14x+1\).
- Responder
-
\({(7x−1)}^2\)
Factorizar una diferencia de cuadrados
Una diferencia de cuadrados es un cuadrado perfecto restado de un cuadrado perfecto. Recordemos que una diferencia de cuadrados se puede reescribir como factores que contienen los mismos términos pero signos opuestos porque los términos medios se cancelan entre sí cuando se multiplican los dos factores.
\[a^2−b^2=(a+b)(a−b)\]
Podemos usar esta ecuación para factorizar cualquier diferencia de cuadrados.
Una diferencia de cuadrados se puede reescribir como dos factores que contienen los mismos términos pero signos opuestos.
\[a^2−b^2=(a+b)(a−b)\]
- Confirmar que el primer y último término son cuadrados perfectos.
- Escribe la forma factorizada como\((a+b)(a−b)\).
Factor\(9x^2−25\).
Solución
Observe que\(9x^2\) y\(25\) son cuadrados perfectos porque\(9x^2={(3x)}^2\) y\(25=5^2\). El polinomio representa una diferencia de cuadrados y se puede reescribir como\((3x+5)(3x−5)\).
Factor\(81y^2−100\).
- Responder
-
\((9y+10)(9y−10)\)
No. Una suma de cuadrados no puede ser factorizada.
Factorización de la suma y diferencia de cubos
Ahora, veremos dos nuevos productos especiales: la suma y diferencia de cubos. Aunque la suma de cuadrados no se puede factorizar, la suma de los cubos se puede factorizar en un binomio y un trinomio.
\[a^3+b^3=(a+b)(a^2−ab+b^2)\]
De igual manera, la suma de cubos se puede factorizar en un binomio y un trinomio, pero con diferentes signos.
\[a^3−b^3=(a−b)(a^2+ab+b^2)\]
Podemos usar el acrónimo SOAP para recordar los signos al factorizar la suma o diferencia de cubos. La primera letra de cada palabra se relaciona con los signos: Mismo Opuesto Siempre Positivo. Por ejemplo, considere el siguiente ejemplo.
\[x^3−2^3=(x−2)(x^2+2x+4)\]
El signo de los 2 primeros es el mismo que el signo entre\(x^3−2^3\). El signo del\(2x\) término es opuesto al signo entre\(x^3−2^3\). Y el signo del último término,\(4\), siempre es positivo.
Podemos factorizar la suma de dos cubos como
\[a^3+b^3=(a+b)(a^2−ab+b^2)\]Podemos factorizar la diferencia de dos cubos como
\[a^3−b^3=(a−b)(a^2+ab+b^2)\]
- Confirmar que el primer y último término son cubos,\(a^3+b^3\) o\(a^3−b^3\).
- Para una suma de cubos, escriba la forma factorizada como\((a+b)(a^2−ab+b^2)\). Para una diferencia de cubos, escriba la forma factorizada como\((a−b)(a^2+ab+b^2)\).
Factor\(x^3+512\).
Solución
Observe que\(x^3\) y\(512\) son cubos porque\(8^3=512\). Reescribe la suma de cubos como\((x+8)(x^2−8x+64)\).
Análisis
Después de escribir la suma de cubos de esta manera, podríamos pensar que deberíamos verificar para ver si la porción trinomial se puede factorizar más. No obstante, la porción trinomial no puede ser factorizada, por lo que no necesitamos verificar.
Factorizar la suma de cubos:\(216a^3+b^3\).
- Responder
-
\((6a+b)(36a^2−6ab+b^2)\)
Factor\(8x^3−125\).
Solución
Observe que\(8x^3\) y\(125\) son cubos porque\(8x^3={(2x)}^3\) y\(125=5^3\). Escribe la diferencia de cubos como\((2x−5)(4x^2+10x+25)\).
Análisis
Al igual que con la suma de cubos, no podremos factorizar aún más la porción trinomial.
Factorizar la diferencia de cubos:\(1000x^3−1\)
- Responder
-
\((10x−1)(100x^2+10x+1)\)
Factorización de expresiones con exponentes fraccionarios o negativos
Las expresiones con exponentes fraccionarios o negativos se pueden factorizar sacando un GCF. Busque la variable o exponente que sea común a cada término de la expresión y saque esa variable o exponente elevado a la potencia más baja. Estas expresiones siguen las mismas reglas de factorización que las que tienen exponentes enteros. Por ejemplo, se\(2x^{\tfrac{1}{4}}+5x^{\tfrac{3}{4}}\) puede factorizar sacando\(x^{\tfrac{1}{4}}\) y siendo reescrito como\(x^{\tfrac{1}{4}}(2+5x^{\tfrac{1}{2}})\).
Factor\(3x{(x+2)}^{-\tfrac{1}{3}}+4{(x+2)}^{\tfrac{2}{3}}\).
Solución
Factorizar el término con el valor más bajo del exponente. En este caso, eso sería\({(x+2)}^{-\tfrac{1}{3}}\).
\[\begin{align*} &(x+2)^{-\tfrac{1}{3}}(3x+4(x+2))\qquad \text{Factor out the GCF }\\ &(x+2)^{-\tfrac{1}{3}}(3x+4x+8)\qquad \text{Simplify } \\ &(x+2)^{-\tfrac{1}{3}}(7x+8) \end{align*}\]
Factor\(2{(5a−1)}^{\tfrac{3}{4}}+7a{(5a−1)}^{−\tfrac{1}{4}}\).
- Responder
-
\({(5a−1)}^{−\tfrac{1}{4}}(17a−2)\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con polinomios de factorización.
2. Trinomios factoriales cuando un es igual a 1
Ecuaciones Clave
| diferencia de cuadrados | \(a^2−b^2=(a+b)(a−b)\) |
| Trinomio cuadrado perfecto | \(a^2+2ab+b^2=(a+b)^2\) |
| suma de cubos | \(a^3+b^3=(a+b)(a^2−ab+b^2)\) |
| diferencia de cubos | \(a^3−b^3=(a−b)(a^2+ab+b^2)\) |
- El mayor factor común, o GCF, puede ser factorizado fuera de un polinomio. La comprobación de un GCF debe ser el primer paso en cualquier problema de factorización. Ver Ejemplo.
- Los trinomios con coeficiente inicial 1 se pueden factorizar encontrando números que tengan un producto del tercer término y una suma del segundo término. Ver Ejemplo.
- Los trinomios se pueden factorizar usando un proceso llamado factorización por agrupación. Ver Ejemplo.
- Los trinomios cuadrados perfectos y la diferencia de cuadrados son productos especiales y se pueden factorizar mediante ecuaciones. Ver Ejemplo y Ejemplo.
- La suma de cubos y la diferencia de cubos se pueden factorizar usando ecuaciones. Ver Ejemplo y Ejemplo.
- Los polinomios que contienen exponentes fraccionarios y negativos se pueden factorizar sacando un GCF. Ver Ejemplo.


