2.4: Modelos y Aplicaciones
- Page ID
- 116836
- Configura una ecuación lineal para resolver una aplicación del mundo real.
- Usa una fórmula para resolver una aplicación del mundo real.
Josh espera obtener una\(A\) en su clase de álgebra universitaria. Tiene puntajes de\(75\)\(82\),\(95\),,\(91\), y\(94\) en sus primeras cinco pruebas. Sólo queda el examen final, y el máximo de puntos que se pueden obtener es\(100\). ¿Es posible que Josh termine el curso con un\(A\)? Una simple ecuación lineal le dará a Josh su respuesta.
Muchas aplicaciones del mundo real se pueden modelar mediante ecuaciones lineales. Por ejemplo, un paquete de teléfono celular puede incluir una tarifa de servicio mensual más un cargo por minuto de tiempo de discusión; le cuesta a un fabricante de widgets una cierta cantidad producir x widgets por mes más cargos operativos mensuales; una compañía de alquiler de autos cobra una tarifa diaria más una cantidad por milla conducida. Estos son ejemplos de aplicaciones con las que nos encontramos todos los días que son modelados por ecuaciones lineales. En esta sección, configuraremos y usaremos ecuaciones lineales para resolver este tipo de problemas.
Configuración de una ecuación lineal para resolver una aplicación del mundo real
Para configurar o modelar una ecuación lineal que se ajuste a una aplicación del mundo real, primero debemos determinar las cantidades conocidas y definir la cantidad desconocida como una variable. Entonces, comenzamos a interpretar las palabras como expresiones matemáticas usando símbolos matemáticos. Usemos el ejemplo de alquiler de autos anterior. En este caso, un costo conocido, como\($0.10/mi\), se multiplica por una cantidad desconocida, el número de millas recorridas. Por lo tanto, podemos escribir\(0.10x\). Esta expresión representa un costo variable porque cambia según el número de millas recorridas.
Si una cantidad es independiente de una variable, normalmente simplemente la sumamos o restamos, según el problema. Como estos montos no cambian, los llamamos costos fijos. Considere una agencia de alquiler de autos que\($0.10/mi\) cobre más una tarifa diaria de\($50\). Podemos usar estas cantidades para modelar una ecuación que se puede utilizar para encontrar el costo diario de alquiler de autos\(C\).
\(C=0.10x+50 \tag{2.4.1}\)
Cuando se trata de aplicaciones del mundo real, hay ciertas expresiones que podemos traducir directamente a las matemáticas. Tabla\(\PageIndex{1}\) enumera algunas expresiones verbales comunes y sus expresiones matemáticas equivalentes.
| Verbal | Traducción a Operaciones Matemáticas |
|---|---|
| Un número supera a otro por un | \(x,x+a\) |
| Dos veces un número | \(2x\) |
| Un número es\(a\) más que otro número | \(x,x+a\) |
| Un número es menos de dos veces otro número | \(x,2x−a\) |
| El producto de un número y\(a\), disminuido en\(b\) | \(ax−b\) |
| El cociente de un número y el número más\(a\) es tres veces el número | \(\dfrac{x}{x+a}=3x\) |
| El producto de tres veces un número y el número disminuido por\(b\) es\(c\) | \(3x(x−b)=c\) |
- Identificar cantidades conocidas.
- Asignar una variable para representar la cantidad desconocida.
- Si hay más de una cantidad desconocida, encuentra la manera de escribir la segunda desconocida en términos de la primera.
- Escribir una ecuación interpretando las palabras como operaciones matemáticas.
- Resuelve la ecuación. Asegúrese de que la solución se pueda explicar con palabras, incluyendo las unidades de medida.
Encuentra una ecuación lineal para resolver para las siguientes cantidades desconocidas: Un número excede a otro número por\( 17\) y su suma es\( 31\). Encuentra los dos números.
Solución
Deja que\( x\) sea igual al primer número. Entonces, como el segundo número supera al primero por\(17\), podemos escribir el segundo número como\( x +17\). La suma de los dos números es\(31\). Usualmente interpretamos la palabra es como un signo igual.
\[\begin{align*} x+(x+17)&= 31\\ 2x+17&= 31\\ 2x&= 14\\ x&= 7 \end{align*}\]
\[\begin{align*} x+17&= 7 + 17\\ &= 24\\ \end{align*}\]
Los dos números son\(7\) y\(24\).
Encuentra una ecuación lineal para resolver para las siguientes cantidades desconocidas: Un número es tres más del doble de otro número. Si la suma de los dos números es\(36\), busque los números.
- Contestar
-
\(11\)y\(25\)
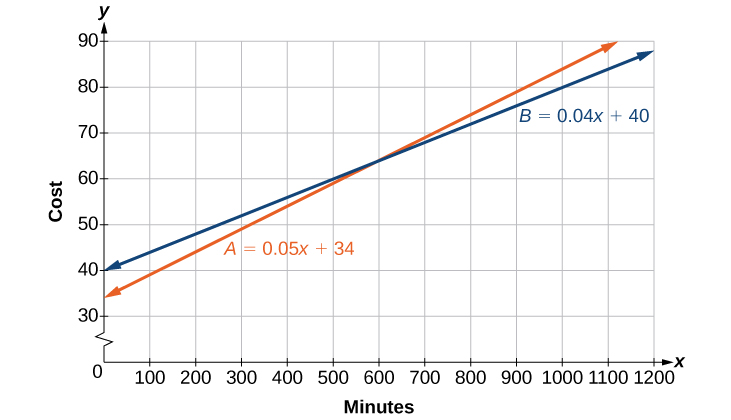
Hay dos compañías de telefonía celular que ofrecen diferentes paquetes. La compañía A cobra una tarifa de servicio mensual de\($34\) más\($.05/min\) tiempo de discusión. La compañía B cobra una tarifa de servicio mensual de\($40\) más\($.04/min\) tiempo de discusión.
- Escribir una ecuación lineal que modele los paquetes ofrecidos por ambas compañías.
- Si el promedio de minutos utilizados cada mes es\(1,160\), ¿qué compañía ofrece el mejor plan?
- Si el promedio de minutos utilizados cada mes es\(420\), ¿qué compañía ofrece el mejor plan?
- ¿Cuántos minutos de tiempo de discusión arrojarían estados de cuenta mensuales iguales de ambas compañías?
Solución
a.
El modelo para la Compañía A se puede escribir como\( A =0.05x+34\). Esto incluye el costo variable de\( 0.05x\) más el cargo mensual por servicio de\($34\). El paquete de la compañía B cobra una tarifa mensual más alta de\($40\), pero un costo variable menor de\( 0.04x\). El modelo de la compañía B se puede escribir como\( B =0.04x+$40\).
b.
Si el promedio de minutos utilizados cada mes es\(1,160\), tenemos lo siguiente:
\[\begin{align*} \text{Company A}&= 0.05(1.160)+34\\ &= 58+34\\ &= 92 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(1,1600)+40\\ &= 46.4+40\\ &= 86.4 \end{align*}\]
Entonces, la Compañía B ofrece el menor costo mensual de en\($86.40\) comparación con el costo\($92\) mensual ofrecido por la Compañía A cuando el número promedio de minutos utilizados cada mes es\(1,160\).
c.
Si el promedio de minutos utilizados cada mes es\(420\), tenemos lo siguiente:
\[\begin{align*} \text{Company A}&= 0.05(420)+34\\ &= 21+34\\ &= 55 \end{align*}\]
\[\begin{align*} \text{Company B}&= 0.04(420)+40\\ &= 16.8+40\\ &= 56.8 \end{align*}\]
Si el número promedio de minutos utilizados cada mes es\(420\), entonces la Compañía A ofrece un costo mensual menor de\($55\) en comparación con el costo mensual de la Compañía B de\($56.80\).
d.
Para responder a la pregunta de cuántos minutos de tiempo de discusión producirían la misma factura de ambas compañías, deberíamos pensar en el problema en términos de\((x,y)\) coordenadas: ¿En qué momento son iguales tanto el\(x\) valor como el\(y\) valor -valor? Podemos encontrar este punto estableciendo las ecuaciones iguales entre sí y resolviendo para\(x\).
\[\begin{align*} 0.05x+34&= 0.04x+40\\ 0.01x&= 6\\ x&= 600 \end{align*}\]Verifique el\(x\) valor -en cada ecuación.
\(0.05(600)+34=64\)
\(0.04(600)+40=64\)
Por lo tanto, un promedio mensual de\(600\) minutos de tiempo de discusión hace que los planes sean iguales. Ver Figura\(\PageIndex{2}\).
Encuentre una ecuación lineal para modelar esta aplicación del mundo real: Le cuesta a la compañía de electrónica ABC\($2.50\) por unidad producir una pieza utilizada en una marca popular de computadoras de escritorio. La compañía tiene gastos operativos mensuales\($350\) de servicios públicos y\($3,300\) salarios. ¿Cuáles son los gastos mensuales de la empresa?
- Contestar
-
\(C=2.5x+3,650\)
Uso de una fórmula para resolver una aplicación del mundo real
Muchas aplicaciones se resuelven usando fórmulas conocidas. Se plantea el problema, se identifica una fórmula, se sustituyen las cantidades conocidas en la fórmula, se resuelve la ecuación para lo desconocido y se responde a la pregunta del problema. Por lo general, estos problemas involucran dos ecuaciones que representan dos viajes, dos inversiones, dos áreas, y así sucesivamente. Ejemplos de fórmulas incluyen el área de una región rectangular,
\[A=LW \tag{2.4.2}\]
el perímetro de un rectángulo,
\[P=2L+2W \tag{2.4.3}\]
y el volumen de un sólido rectangular,
\[V=LWH. \tag{2.4.4}\]
Cuando hay dos incógnitas, encontramos la manera de escribir una en términos de la otra porque solo podemos resolver para una variable a la vez.
Se necesita Andrew\(30\; min\) para conducir al trabajo por la mañana. Conduce a casa usando la misma ruta, pero lleva\(10\; min\) más tiempo, y promedia\(10\; mi/h\) menos que en la mañana. ¿A qué distancia conduce Andrew para trabajar?
Solución
Esto es un problema de distancia, por lo que podemos usar la fórmula\(d =rt\), donde la distancia equivale a tasa multiplicada por el tiempo. Tenga en cuenta que cuando se da la tarifa\(mi/h\), el tiempo debe expresarse en horas. Las unidades de medida consistentes son clave para obtener una solución correcta.
Primero, identificamos las cantidades conocidas y desconocidas. El viaje matutino de Andrew al trabajo toma\(30\; min\), o\(12\; h\) al ritmo\(r\). Su viaje a casa toma\(40\; min\), o\(23\; h\), y su velocidad promedia\(10\; mi/h\) menos que la conducción matutina. Ambos viajes cubren distancia\(d\). Una tabla, como Table\(\PageIndex{2}\), suele ser útil para realizar un seguimiento de la información en este tipo de problemas.
| \(d\) | \(r\) | \(t\) | |
|---|---|---|---|
| Para Trabajar | \ (d\)” style="text-align:center;” class="lt-math-1632">\(d\) | \ (r\)” style="text-align:center;” class="lt-math-1632">\(r\) | \ (t\)” style="text-align:center;” class="lt-math-1632">\(12\) |
| A Casa | \ (d\)” style="text-align:center;” class="lt-math-1632">\(d\) | \ (r\)” style="text-align:center;” class="lt-math-1632">\(r−10\) | \ (t\)” style="text-align:center;” class="lt-math-1632">\(23\) |
Escribe dos ecuaciones, una para cada viaje.
\[d=r\left(\dfrac{1}{2}\right) \qquad \text{To work} \nonumber\]
\[d=(r-10)\left(\dfrac{2}{3}\right) \qquad \text{To home} \nonumber\]
Como ambas ecuaciones igualan la misma distancia, las establecemos iguales entre sí y resolvemos para\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right )&= (r-10)\left (\dfrac{2}{3} \right )\\ \dfrac{1}{2r}&= \dfrac{2}{3}r-\dfrac{20}{3}\\ \dfrac{1}{2}r-\dfrac{2}{3}r&= -\dfrac{20}{3}\\ -\dfrac{1}{6}r&= -\dfrac{20}{3}\\ r&= -\dfrac{20}{3}(-6)\\ r&= 40 \end{align*}\]
Hemos resuelto por la tasa de velocidad para trabajar,\(40\; mph\). Sustituir\(40\) en la tarifa en el viaje de regreso rinde\(30 mi/h\). Ahora ya podemos responder a la pregunta. Sustituya la tasa de nuevo en cualquiera de las ecuaciones y resuelva para\(d\).
\[\begin{align*}d&= 40\left (\dfrac{1}{2} \right )\\ &= 20 \end{align*}\]
La distancia entre el hogar y el trabajo es\(20\; mi\).
Análisis
Tenga en cuenta que podríamos haber aclarado las fracciones en la ecuación multiplicando ambos lados de la ecuación por la LCD para resolver\(r\).
\[\begin{align*} r\left (\dfrac{1}{2} \right)&= (r-10)\left (\dfrac{2}{3} \right )\\ 6\times r\left (\dfrac{1}{2} \right)&= 6\times (r-10)\left (\dfrac{2}{3} \right )\\ 3r&= 4(r-10)\\ 3r&= 4r-40\\ r&= 40 \end{align*}\]
El sábado por la mañana, Jennifer tardó en conducir\(3.6\; h\) hasta la casa de su madre para el fin de semana. El domingo por la noche, debido al fuerte tráfico, Jennifer tardó en regresar\(4\; h\) a casa. Su velocidad fue\(5\; mi/h\) más lenta el domingo que el sábado. ¿Cuál era su velocidad el domingo?
- Contestar
-
\(45\; mi/h\)
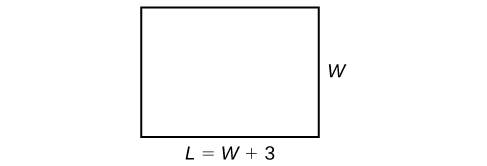
El perímetro de un patio exterior rectangular es\(54\; ft\). El largo es\(3\; ft\) mayor que el ancho. ¿Cuáles son las dimensiones del patio?
Solución
La fórmula perimetral es estándar:\(P=2L+2W\). Tenemos dos cantidades desconocidas, largo y ancho. Sin embargo, podemos escribir la longitud en términos del ancho como\(L =W+3\). Sustituya el valor de perímetro y la expresión de longitud en la fórmula. A menudo es útil hacer un boceto y etiquetar los lados como en la Figura\(\PageIndex{3}\).
Ahora podemos resolver para el ancho y luego calcular el largo.
\[\begin{align*} P&= 2L + 2W\\ 54&= 2(W+3)+2W\\ 54&= 2W+6+2W\\ 54&= 4W+6\\ 48&= 4W\\ W&= 12 \end{align*}\]
\[\begin{align*} L&= 12+3\\ L&= 15 \end{align*}\]
Las dimensiones son\(L = 15\; ft\) y\(W = 12\; ft\).
Encuentra las dimensiones de un rectángulo dado que el perímetro es\(110\; cm\) y la longitud es\(1\; cm\) más del doble de la anchura.
- Contestar
-
\(L=37\; cm\),\(W=18\; cm\)
El perímetro de una tableta de papel cuadriculado es\(48\space{in.}^2\). El largo es\(6\; in\). más que el ancho. Encuentra el área del papel cuadrificado.
Solución
La fórmula estándar para el área es\(A =LW\); sin embargo, resolveremos el problema usando la fórmula perimetral. La razón por la que usamos la fórmula perimetral es porque conocemos suficiente información sobre el perímetro que la fórmula nos permitirá resolver para una de las incógnitas. Como tanto el perímetro como el área utilizan el largo y el ancho como dimensiones, a menudo se usan juntos para resolver un problema como este.
Sabemos que la longitud es\(6\; in\). más que la anchura, así podemos escribir longitud como\(L =W+6\). Sustituir el valor del perímetro y la expresión de longitud en la fórmula perimetral y encontrar la longitud.
\[\begin{align*} P&= 2L + 2W\\ 48&= 2(W+6)+2W\\ 48&= 2W+12+2W\\ 48&= 4W+12\\ 36&= 4W\\ W&= 9 \end{align*}\]
\[\begin{align*}L&= 9+6\\ L&= 15 \end{align*}\]
Ahora, encontramos el área dadas las dimensiones de\(L = 15\; in\). y\(W = 9\; in\).
\[\begin{align*} A&= LW\\ A&=15(9)\\ A&= 135\space{in.}^2 \end{align*}\]
El área es\(135\space{in.}^2\).
Una sala de juegos tiene un perímetro de\(70\; ft\). El largo es de cinco más del doble de ancho. ¿Cuántas\(ft^2\) alfombras nuevas se deben pedir?
- Contestar
-
\(250\space{ft}^2\)
Encuentra las dimensiones de una caja de envío dado que el largo es el doble de ancho, la altura es\(8\; \) adentro y el volumen es\(1,600\space{in.}^3\).
Solución
La fórmula para el volumen de una caja se da como\(V =LWH\), el producto de largo, ancho y alto. Se nos da eso\(L =2W\), y\(H =8\). El volumen es\(1,600\; \text{cubic inches}\).
\[\begin{align*} V&= LWH\\ 1600&= (2W)W(8)\\ 1600&= 16W^2\\ 100&= W^2\\ 10&= W \end{align*}\]Las dimensiones son\(L = 20\; in\),\(W= 10\; in\), y\(H = 8\; in\).
Análisis
Tenga en cuenta que la raíz cuadrada de\(W^2\) resultaría en un valor positivo y otro negativo. Sin embargo, debido a que estamos describiendo el ancho, podemos usar solo el resultado positivo.
Acceda a estos recursos en línea para obtener instrucción y práctica adicional con modelos y aplicaciones de ecuaciones lineales.
- Resolución de problemas usando ecuaciones lineales
- Resolución de problemas usando ecuaciones
- Encontrar las dimensiones del área dado el perímetro
- Encuentra la distancia entre las ciudades usando la fórmula distance = rate * time
- Aplicación de ecuaciones lineales (Escribir una ecuación de costo)
Conceptos clave
- Una ecuación lineal puede ser utilizada para resolver un problema desconocido en un número. Ver Ejemplo.
- Las aplicaciones se pueden escribir como problemas matemáticos identificando cantidades conocidas y asignando una variable a cantidades desconocidas. Ver Ejemplo.
- Existen muchas fórmulas conocidas que se pueden utilizar para resolver aplicaciones. Los problemas de distancia, por ejemplo, se resuelven usando la\(d = rt\) fórmula. Ver Ejemplo.
- Muchos problemas de geometría se resuelven usando la fórmula perimetral\(P =2L+2W\), la fórmula\(A =LW\) de área o la fórmula de volumen\(V =LWH\). Ver Ejemplo, Ejemplo y Ejemplo.