2.3: Ecuaciones lineales en una variable
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Resolver ecuaciones en una variable algebraicamente.
- Resolver una ecuación racional.
- Encuentra una ecuación lineal.
- Dadas las ecuaciones de dos líneas, determinar si sus gráficas son paralelas o perpendiculares.
- Escribe la ecuación de una línea paralela o perpendicular a una línea dada.
Caroline es una estudiante universitaria de tiempo completo que planea unas vacaciones de primavera. Para ganar suficiente dinero para el viaje, ha tomado un trabajo de medio tiempo en el banco local que paga$15.00/hr, y abrió una cuenta de ahorros con un depósito inicial del 15 de$400 enero. Ella arregló el depósito directo de sus cheques de nómina. Si las vacaciones de primavera comienzan el 20 de marzo y el viaje costará aproximadamente$2,500, ¿cuántas horas tendrá que trabajar para ganar lo suficiente para pagar sus vacaciones? Si sólo puede trabajar4 horas por día, ¿cuántos días a la semana tendrá que trabajar? ¿Cuántas semanas tomará? En esta sección, investigaremos problemas como este y otros, los cuales generan gráficas como la línea en la Figura2.3.1.
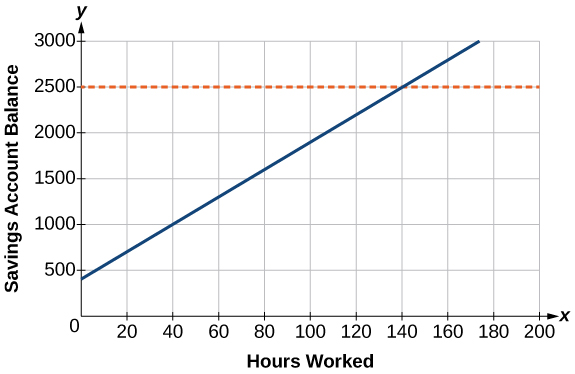
Resolver ecuaciones lineales en una variable
Una ecuación lineal es una ecuación de una línea recta, escrita en una variable. La única potencia de la variable es1. Las ecuaciones lineales en una variable pueden tomar la formaax+b=0 y se resuelven mediante operaciones algebraicas básicas. Comenzamos clasificando las ecuaciones lineales en una variable como uno de tres tipos: identidad, condicional o inconsistente.
- Una ecuación de identidad es verdadera para todos los valores de la variable. He aquí un ejemplo de una ecuación de identidad:3x=2x+xEl conjunto de soluciones consiste en todos los valores que hacen que la ecuación sea verdadera. Para esta ecuación, el conjunto de soluciones son todos números reales porque cualquier número real sustituidox hará que la ecuación sea verdadera.
- Una ecuación condicional es verdadera solo para algunos valores de la variable. Por ejemplo, si vamos a resolver la ecuación5x+2=3x−6, tenemos lo siguiente:5x+2=3x−62x=−8x=−4El conjunto de soluciones consta de un número:−4. Es la única solución y, por tanto, hemos resuelto una ecuación condicional.
- Una ecuación inconsistente da como resultado una declaración falsa. Por ejemplo, si vamos a resolver5x−15=5(x−4), tenemos lo siguiente:5x−15=5x−205x−15−5x=5x−20−5x−15≠−20Efectivamente,−15≠−20. No hay solución porque se trata de una ecuación inconsistente.
Resolver ecuaciones lineales en una variable implica las propiedades fundamentales de la igualdad y las operaciones algebraicas básicas. A continuación se presenta una breve revisión de esas operaciones.
Una ecuación lineal en una variable se puede escribir en la forma
ax+b=0
donde a y b son números reales,a≠0.
Los siguientes pasos se utilizan para manipular una ecuación y aislar la variable desconocida, de manera que la última línea digax= _________, six es la desconocida. No hay un orden establecido, ya que los pasos utilizados dependen de lo que se dé:
- Podemos sumar, restar, multiplicar o dividir una ecuación por un número o una expresión siempre y cuando hagamos lo mismo a ambos lados del signo igual. Tenga en cuenta que no podemos dividir por cero.
- Aplicar la propiedad distributiva según sea necesario:a(b+c)=ab+ac.
- Aísle la variable en un lado de la ecuación.
- Cuando la variable se multiplica por un coeficiente en la etapa final, multiplique ambos lados de la ecuación por el recíproco del coeficiente.
Resuelve la siguiente ecuación:2x+7=19.
Solución
Esta ecuación se puede escribir en la formaax+b=0 restando 19 de ambos lados. Sin embargo, podemos proceder a resolver la ecuación en su forma original realizando operaciones algebraicas.
2x+7=192x=12Subtract 7 from both sidesx=6Multiply both sides by 12 or divide by 2
La solución es6.
Resolver la ecuación lineal en una variable:2x+1=−9.
- Contestar
-
x=−5
Resuelve la siguiente ecuación:4(x−3)+12=15−5(x+6).
Solución
Aplicar propiedades algebraicas estándar.
4(x−3)+12=15−5(x+6)4x−12+12=15−5x−30Apply the distributive property4x=−15−5xCombine like terms9x=−15Place x terms on one side and simplifyx=−159Multiply both sides by 19 , the reciprocal of 9x=−53
Análisis
Este problema requiere que la propiedad distributiva se aplique dos veces, y luego se utilizan las propiedades del álgebra para llegar a la línea final,x=−53.
Resolver la ecuación en una variable:−2(3x−1)+x=14−x.
- Contestar
-
x=−3
Resolviendo una ecuación racional
En esta sección, observamos ecuaciones racionales que, después de alguna manipulación, dan como resultado una ecuación lineal. Si una ecuación contiene al menos una expresión racional, se considera una ecuación racional. Recordemos que un número racional es la relación de dos números, como23 o72. Una expresión racional es la relación, o cociente, de dos polinomios. Aquí hay tres ejemplos.
x+1x2−4
1x−3
o
4x2+x−2
Las ecuaciones racionales tienen una variable en el denominador en al menos uno de los términos. Nuestro objetivo es realizar operaciones algebraicas para que las variables aparezcan en el numerador. De hecho, eliminaremos todos los denominadores multiplicando ambos lados de la ecuación por el mínimo denominador común (LCD). Encontrar el LCD es identificar una expresión que contiene la mayor potencia de todos los factores en todos los denominadores. Hacemos esto porque cuando la ecuación se multiplica por la LCD, los factores comunes en la LCD y en cada denominador serán iguales a uno y cancelarán.
Resolver la ecuación racional:
72x−53x=223
Solución
Tenemos tres denominadores;2x,3x, y3. La pantalla LCD debe contener2x,3x, y3. Un LCD de6x contiene los tres denominadores. Es decir, cada denominador se puede dividir de manera uniforme en la LCD. A continuación, multiplique ambos lados de la ecuación por la LCD6x.
\ [\ begin {align*}
(6x)\ izquierda [\ dfrac {7} {2x} -\ dfrac {5} {3x}\ derecha] &=\ izquierda [\ dfrac {22} {3}\ derecha] (6x)\ (6x)\ izquierda (\ dfrac {7} {2x}\ derecha) -
(6x)\ izquierda (\ dfrac {7} {2x}\ derecha) - (6x)\ izquierda (\ dfrac {7} {2x}\ derecha) - ac {5} {3x}\ right) &=\ left (\ dfrac {22} {3}\ right) (6x)\ qquad\ text {Usa la propiedad distributiva. Cancelar los factores comunes}\\
3 (7) -2 (5) &=22 (2x)\ qquad\ text {Multiplica los factores restantes por cada numerador.} \\
21-10&=44x\\
11&=44x\
\ dfrac {11} {44} &=x\
\ dfrac {1} {4} &=x
\ end {alinear*}\]
Un error común que se comete al resolver ecuaciones racionales implica encontrar la LCD cuando uno de los denominadores es un binomio, dos términos agregados o restados, como(x+1). Siempre considere un binomio como un factor individual, los términos no se pueden separar. Por ejemplo, supongamos que un problema tiene tres términos y los denominadores sonx,x−1, y3x−3. Primero, factorizar todos los denominadores. Entonces tenemosx,(x−1), y3(x−1) como los denominadores. (Tenga en cuenta los paréntesis colocados alrededor del segundo denominador.) Sólo los dos últimos denominadores tienen un factor común de(x−1). La x en el primer denominador es separada de lax en los(x−1) denominadores. Una manera efectiva de recordar esto es escribir denominadores factorizados y binomiales entre paréntesis, y considerar cada paréntesis como una unidad separada o un factor separado. El LCD en esta instancia se encuentra multiplicando juntos elx, un factor de(x−1), y el 3. Así, la pantalla LCD es la siguiente:
x(x−1)3=3x(x−1)
Entonces, ambos lados de la ecuación se multiplicarían por3x(x−1). Deja la pantalla LCD en forma factorizada, ya que esto facilita ver cómo se cancela cada denominador del problema.
Otro ejemplo es un problema con dos denominadores, comox yx2+2x. Una vez que se factoriza el segundo denominador comox2+2x=x(x+2), hay un factor común dex en ambos denominadores y el LCD esx(x+2).
A veces tenemos una ecuación racional en forma de proporción; es decir, cuando una fracción equivale a otra fracción y no hay otros términos en la ecuación.
ab=cd
Podemos usar otro método para resolver la ecuación sin encontrar la LCD: multiplicación cruzada. Multiplicamos términos cruzando sobre el signo igual.
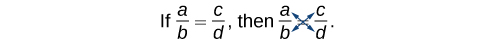
Multiplicar a (d) y b (c), lo que resulta enad=bc.
Cualquier solución que haga que un denominador en la expresión original sea igual a cero debe ser excluida de las posibilidades.
Una ecuación r acional contiene al menos una expresión racional donde la variable aparece en al menos uno de los denominadores.
- Factorizar todos los denominadores en la ecuación.
- Encuentra y excluye valores que establecen cada denominador igual a cero.
- Encuentra la pantalla LCD.
- Multiplique toda la ecuación por la pantalla LCD. Si la pantalla LCD es correcta, no quedarán denominadores.
- Resuelve la ecuación restante.
- Asegúrese de verificar las soluciones en las ecuaciones originales para evitar que una solución produzca cero en un denominador
Resuelve la siguiente ecuación racional:
2x−32=72x
SoluciónTenemos tres denominadores:x,2, y2x. No se requiere factorización. El producto de los dos primeros denominadores es igual al tercer denominador, entonces, el LCD es2x. Solo se excluye un valor de un conjunto de soluciones,0. A continuación, multiplique toda la ecuación (ambos lados del signo igual) por2x.
2x[2x−32]=[72x](2x)2x(2x)−2x(32)=(72x)(2x)Distribute 2x2(2)−3x=7Denominators cancel out.4−3x=7−3x=3x=−1 or {−1}
La solución propuesta es−1, que no es un valor excluido, por lo que el conjunto de soluciones contiene un númerox=−1, o{−1} escrito en notación de conjunto.
Resolver la ecuación racional:
23x=14−16x
- Contestar
-
x=103
Resuelve la siguiente ecuación racional:
1x=110−34x
Solución
Primero encuentra el denominador común. Los tres denominadores en forma factorizada sonx,10=2⋅5, y4x=2⋅2⋅x. La expresión más pequeña que es divisible por cada uno de los denominadores es20x. Solox=0 es un valor excluido. Multiplique toda la ecuación por20x.
20x(1x)=(110−34x)20x20=2x−1535=2x352=x
La solución es352.
Resolver la ecuación racional:
−52x+34x=−74
- Contestar
-
x=1
Resuelve las siguientes ecuaciones racionales y establece los valores excluidos:
- 3x−6=5x
- xx−3=5x−3−12
- xx−2=5x−2−12
Solución
a.
Los denominadoresx y nox−6 tienen nada en común. Por lo tanto, el LCD es el productox(x−6). Sin embargo, para este problema, podemos cruzarlo.
3x−6=5x3x=5(x−6)Distribute.3x=5x−30−2x=−30x=15
La solución es15. Los valores excluidos son6 y0.
b.
El LCD es2(x−3). Multiplique ambos lados de la ecuación por2(x−3).
2(x−3)[xx−3]=[5x−3−12]2(x−3)2(x−3)xx−3=2(x−3)5x−3−2(x−3)22x=10−(x−3)2x=13−x3x=13x=133
La solución es133. El valor excluido es3.
c.
El mínimo denominador común es2(x−2). Multiplique ambos lados de la ecuación porx(x−2).
2(x−2)[xx−2]=[5x−2−12]2(x−2)2x=10−(x−2)2x=12−x3x=12x=4
La solución es4. El valor excluido es2.
Resolver−32x+1=43x+1. Exponer los valores excluidos.
- Contestar
-
x=−717. Los valores excluidos sonx=−12 yx=−13.
Resolver la ecuación racional después de factorizar los denominadores:2x+1−1x−1=2xx2−1. Exponer los valores excluidos.
Solución
Debemos factorizar el denominadorx2−1. Reconocemos esto como la diferencia de cuadrados, y la factorizamos como(x−1)(x+1). Así, la LCD que contiene cada denominador es(x−1)(x+1). Multiplique toda la ecuación por la LCD, cancele los denominadores y resuelva la ecuación restante.
(x+1)(x−1)[2x+1−1x−1]=[2xx2−1](x+1)(x−1)2(x−1)−(x+1)=2x2x−2−x−1=2x Distribute the negative sign−3−x=0x=−3
La solución es−3. Los valores excluidos son1 y−1.
Resolver la ecuación racional:
2x−2+1x+1=1x2−x−2
- Contestar
-
x=13
Encontrar una ecuación lineal
Quizás la forma más familiar de una ecuación lineal es la forma pendiente-intercepción, escrita comoy=mx+b
La pendiente de una línea se refiere a la relación del cambio verticaly sobre el cambio horizontalx entre dos puntos cualesquiera de una línea. Indica la dirección en la que una línea se inclina así como su inclinación. La pendiente a veces se describe como subida sobre carrera.
Si la pendiente es positiva, la línea se inclinará hacia la derecha. Si la pendiente es negativa, la línea se inclinará hacia la izquierda. A medida que aumenta la pendiente, la línea se vuelve más pronunciada. Algunos ejemplos se muestran en la Figura2.3.2. Las líneas indican las siguientes pendientes:m=−3,m=2, ym=13.
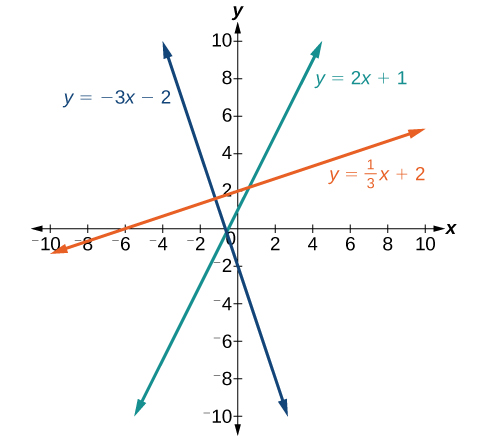
La pendiente de una línea,m, representa el cambio eny sobre el cambio enx. Dados dos puntos,(x1,y1) y(x2,y2), la siguiente fórmula determina la pendiente de una línea que contiene estos puntos:
m=y2−y1x2−x1
Encuentra la pendiente de una línea que pasa por los puntos(2,−1) y(−5,3).
Solución
Sustituimos losy valores -y losx valores -en la fórmula.
m=3−(−1)−5−2=4−7=−47
La pendiente es−47
Análisis
No importa qué punto se llame(x1,y1) o(x2,y2). Siempre y cuando seamos consistentes con el orden de losy términos y el orden de losx términos en el numerador y denominador, el cálculo arrojará el mismo resultado.
Encuentra la pendiente de la línea que pasa por los puntos(−2,6) y(1,4).
- Contestar
-
m=−23
Identificar la pendiente yy -interceptar, dada la ecuacióny=−34x−4.
Solución
Como la línea está eny=mx+b forma, la línea dada tiene una pendiente dem=−34. Ely -intercepto esb=−4.
Análisis
Lay intersección es el punto en el que la línea cruza ely eje. En ely eje -,x=0. Siempre podemos identificar lay -intercepción cuando la línea está en forma de pendiente-intercepción, ya que siempre será igualb. O, simplemente sustituirlox=0 y resolver pory.
La fórmula de punto-pendiente
Dada la pendiente y un punto en una línea, podemos encontrar la ecuación de la línea usando la fórmula punto-pendiente.
y−y1=m(x−x1)
Esta es una fórmula importante, ya que se utilizará en otras áreas del álgebra universitaria y muchas veces en el cálculo para encontrar la ecuación de una línea tangente. Solo necesitamos un punto y la pendiente de la línea para usar la fórmula. Después de sustituir la pendiente y las coordenadas de un punto en la fórmula, la simplificamos y la escribimos en forma de pendiente-intercepción.
Dado un punto y la pendiente, la fórmula punto-pendiente conducirá a la ecuación de una línea:
y−y1=m(x−x1)
Escribe la ecuación de la línea con pendientem=−3 y pasando por el punto(4,8). Escribe la ecuación final en forma de pendiente-intersección.
Solución
Usando la fórmula punto-pendiente, sustituya−3 m y el punto(4,8) por(x1,y1).
y−y1=m(x−x1)y−8=−3(x−4)y−8=−3x+12y=−3x+20
Análisis
Tenga en cuenta que cualquier punto de la línea se puede utilizar para encontrar la ecuación. Si se hace correctamente, se obtendrá la misma ecuación final.
Dadom=4, encuentra la ecuación de la línea en forma pendiente-intercepción pasando por el punto(2,5).
- Contestar
-
y=4x−3
Encuentra la ecuación de la línea que pasa por los puntos(3,4) y(0,−3). Escribe la ecuación final en forma de pendiente-intersección.
Solución
Primero, calculamos la pendiente usando la fórmula de pendiente y dos puntos.
m=−3−40−3m=−7−3m=73
A continuación, usamos la fórmula punto-pendiente con la pendiente de73, y cualquiera de los puntos. Escojamos el punto(3,4) para(x1,y1).
y−4=73(x−3)y−4=73x−7y=73x−3
En forma de pendiente-intersección, la ecuación se escribe comoy=73x−3
Análisis
Para probar que se puede utilizar cualquiera de los dos puntos, usemos el segundo punto(0,−3) y veamos si obtenemos la misma ecuación.
y−(−3)=73(x−0)y+3=73xy=73x−3
Vemos que se obtendrá la misma línea usando cualquiera de los dos puntos. Esto tiene sentido porque utilizamos ambos puntos para calcular la pendiente.
Forma estándar de una línea
Otra forma en la que podemos representar la ecuación de una línea es en forma estándar. La forma estándar se da como
Ax+By=C
dondeA,B, yC son números enteros. Losy términosx - y -están en un lado del signo igual y el término constante está en el otro lado.
Encuentra la ecuación de la línea conm=−6 y pasando por el punto(14,−2). Escribe la ecuación en forma estándar.
Solución
Comenzamos a usar la fórmula de punto-pendiente.
y−(−2)=−6(x−14)y+2=−6x+32
A partir de aquí, multiplicamos por2, ya que no se permiten fracciones en forma estándar, para luego mover ambas variables a la izquierda al lado del signo igual y mover las constantes hacia la derecha.
2(y+2)=(−6x+32)22y+4=−12x+312x+2y=−1
Esta ecuación ahora está escrita en forma estándar.
Encuentra la ecuación de la línea en forma estándar con pendientem=−13 y pasando por el punto(1,13).
- Contestar
-
x+3y=2
Líneas verticales y horizontales
Las ecuaciones de líneas verticales y horizontales no requieren ninguna de las fórmulas anteriores, aunque podemos usar las fórmulas para demostrar que las ecuaciones son correctas. La ecuación de una línea vertical se da como
dondec es una constante. La pendiente de una línea vertical es indefinida, e independientemente dely valor -valor de cualquier punto de la línea, lax coordenada -del punto serác.
Supongamos que queremos encontrar la ecuación de una línea que contenga los siguientes puntos:(−3,−5),(−3,1),(−3,3), y(−3,5). Primero, encontraremos la pendiente.
Cero en el denominador significa que la pendiente es indefinida y, por lo tanto, no podemos usar la fórmula punto-pendiente. No obstante, podemos trazar los puntos. Observe que todas lasx coordenadas son iguales y nos encontramos con una línea vertical a travésx=−3. Ver Figura2.3.3.
La ecuación de una línea horizontal se da como
y=c
dondec es una constante. La pendiente de una línea horizontal es cero, y para cualquierx valor -valor de un punto en la línea, lay coordenada -serác.
Supongamos que queremos encontrar la ecuación de una línea que contenga el siguiente conjunto de puntos:(−2,−2),(0,−2),(3,−2), y(5,−2). Podemos usar la fórmula punto-pendiente. Primero, encontramos la pendiente usando dos puntos cualesquiera en la línea.
m=−2−(−2)0−(−2)=02=0
Usa cualquier punto para(x1,y1) en la fórmula, o usa la intersección y.
y−(−2)=0(x−3)y+2=0y=−2
La gráfica es una línea horizontal a travésy=−2. Observe que todas las coordenadas y son iguales. Ver Figura2.3.3.
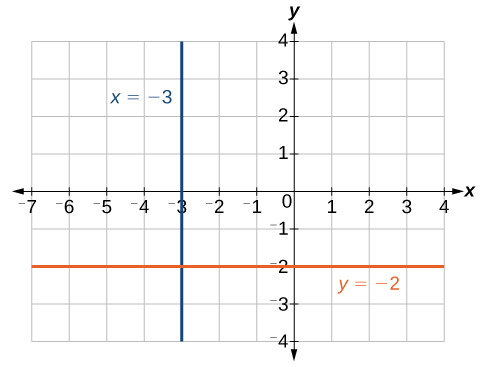
Encuentra la ecuación de la línea que pasa por los puntos dados:(1,−3) y(1,4).
Solución
Lax coordenada -de ambos puntos es1. Por lo tanto, tenemos una línea vertical,x=1.
Encuentra la ecuación de la línea que pasa por(−5,2) y(2,2).
- Contestar
-
Línea horizontal:y=2
Determinar si las gráficas de líneas son paralelas o perpendiculares
Las líneas paralelas tienen la misma pendiente y diferentes intercepciones en Y. Las líneas que son paralelas entre sí nunca se cruzarán. Por ejemplo, la Figura2.3.4 muestra las gráficas de diversas líneas con la misma pendiente,m=2.
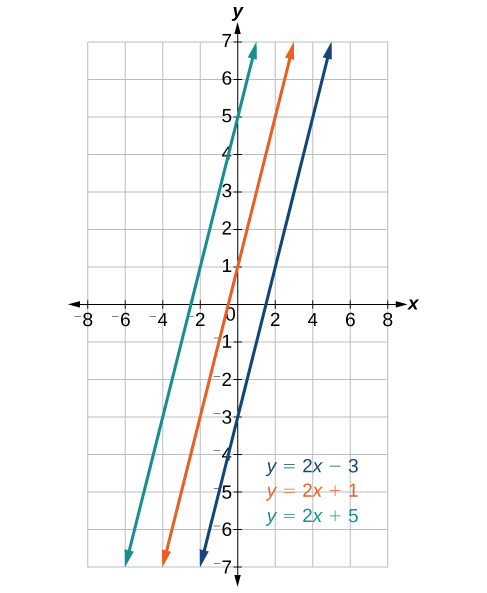
Todas las líneas que se muestran en la gráfica son paralelas porque tienen la misma pendiente y diferentes intercepciones en Y.
Las líneas perpendiculares se cruzan para formar un90∘ ángulo. La pendiente de una línea es el recíproco negativo de la otra. Podemos mostrar que dos líneas son perpendiculares si el producto de las dos pendientes es−1:m1⋅m2=−1. Por ejemplo, la Figura2.3.5 muestra la gráfica de dos líneas perpendiculares. Una línea tiene una pendiente de3; la otra línea tiene una pendiente de−13.
m1⋅m2=−13⋅(−13)=−1
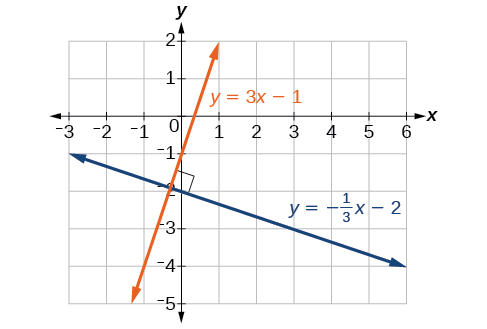
Grafique las ecuaciones de las líneas dadas, y establezca si son paralelas, perpendiculares o ninguna:3y=−4x+3 y3x−4y=8.
Solución
Lo primero que queremos hacer es reescribir las ecuaciones para que ambas ecuaciones estén en forma de pendiente-intercepción.
Primera ecuación:
3y=−4x+3y=−43x+1
Segunda ecuación:
3x−4y=8−4y=−3x+8y=34x−2
Consulte la gráfica de ambas líneas en la Figura2.3.6.
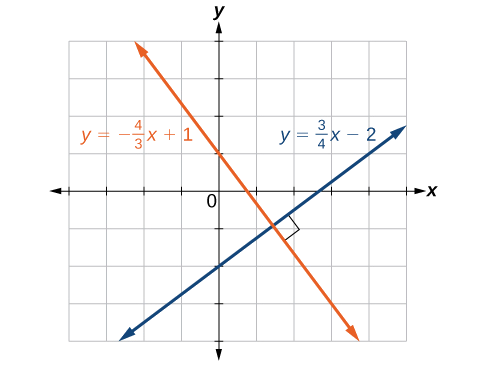
De la gráfica, podemos ver que las líneas aparecen perpendiculares, pero debemos comparar las pendientes.
m1=−43m2=34m1⋅m2=(−43)(34)=−1
Las pendientes son recíprocas negativas entre sí, lo que confirma que las líneas son perpendiculares.
Grafica las dos líneas y determina si son paralelas, perpendiculares o ninguna:2y−x=10 y2y=x+4.
- Contestar
-
Líneas paralelas: las ecuaciones se escriben en forma de pendiente-intersección.
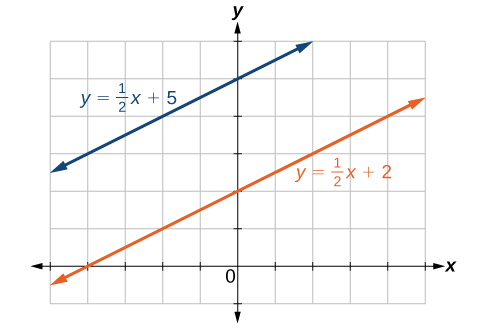
Figura2.3.7
Escribir las ecuaciones de líneas paralelas o perpendiculares a una línea dada
Como hemos aprendido, determinar si dos líneas son paralelas o perpendiculares es cuestión de encontrar las pendientes. Para escribir la ecuación de una línea paralela o perpendicular a otra línea, seguimos los mismos principios que hacemos para encontrar la ecuación de cualquier línea. Después de encontrar la pendiente, utilice la fórmula de punto-pendiente para escribir la ecuación de la nueva línea.
- Encuentra la pendiente de la línea dada. La forma más fácil de hacerlo es escribir la ecuación en forma de pendiente-intercepción.
- Utilice la pendiente y el punto dado con la fórmula de punto-pendiente.
- Simplifique la forma de línea para interceptar pendiente y compare la ecuación con la línea dada.
Escribe la ecuación de línea paralela a a5x+3y=1 y pasando por el punto(3,5).
Solución
Primero, escribiremos la ecuación en forma de pendiente-intersección para encontrar la pendiente.
5x+3y=13y=−5x+1y=−53x+13
La pendiente esm=−53. La intercepción y es13, pero eso realmente no entra en nuestro problema, ya que lo único que necesitamos para que dos líneas sean paralelas es la misma pendiente. La única excepción es que si lasy -intercepciones son iguales, entonces las dos líneas son la misma línea. El siguiente paso es usar esta pendiente y el punto dado con la fórmula punto-pendiente.
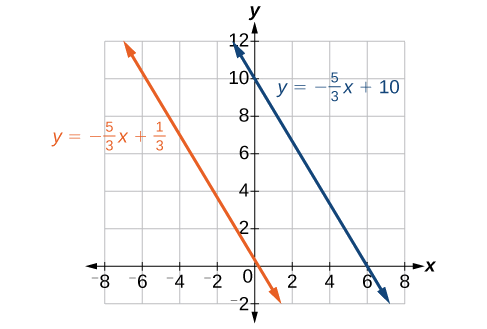
y−5=−53(x−3)y−5=−53x+5y=−53x+10
La ecuación de la línea esy=−53x+10. Ver Figura2.3.8.
Encuentra la ecuación de la línea paralela5x=7+y y que pasa por el punto(−1,−2).
- Contestar
-
y=5x+3
Encuentra la ecuación de la línea perpendicular a5x−3y+4=0 (−4,1).
Solución
El primer paso es escribir la ecuación en forma de pendiente-intersección.
5x−3y+4=0−3y=−5x−4y=53x+43
Vemos que la pendiente esm=53. Esto significa que la pendiente de la línea perpendicular a la línea dada es el recíproco negativo, o−35. A continuación, utilizamos la fórmula de punto-pendiente con esta nueva pendiente y el punto dado.
y−1=−35(x−(−4))y−1=−35x−125y=−35x−125+55y=−35x−75
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con ecuaciones lineales.
- Resolver ecuaciones racionales
- Ecuación de una línea dada dos puntos
- Encontrar la ecuación de una línea perpendicular a otra línea a través de un punto dado
- Encontrar la ecuación de una línea paralela a otra línea a través de un punto dado
Conceptos clave
- Podemos resolver ecuaciones lineales en una variable en la formaax+b=0 usando propiedades algebraicas estándar. Ver Ejemplo y Ejemplo.
- Una expresión racional es un cociente de dos polinomios. Utilizamos la LCD para borrar las fracciones de una ecuación. Ver Ejemplo y Ejemplo.
- Todas las soluciones a una ecuación racional deben verificarse dentro de la ecuación original para evitar un término indefinido, o cero en el denominador. Ver Ejemplo y Ejemplo.
- Dados dos puntos, podemos encontrar la pendiente de una línea usando la fórmula de pendiente. Ver Ejemplo.
- Podemos identificar la pendiente ey intercepción de una ecuación en forma de pendiente-intercepción. Ver Ejemplo.
- Podemos encontrar la ecuación de una línea dada la pendiente y un punto. Ver Ejemplo.
- También podemos encontrar la ecuación de una línea dada dos puntos. Encuentra el talud y usa la fórmula punto-pendiente. Ver Ejemplo.
- La forma estándar de una línea no tiene fracciones. Ver Ejemplo.
- Las líneas horizontales tienen una pendiente de cero y se definen comoy=c, dondec es una constante.
- Las líneas verticales tienen una pendiente indefinida (cero en el denominador), y se definen como \(x=c\), dondec es una constante. Ver Ejemplo.
- Las líneas paralelas tienen la misma pendiente y diferentesy -intercepciones. Ver Ejemplo.
- Las líneas perpendiculares tienen pendientes que son recíprocas negativas entre sí a menos que una sea horizontal y la otra sea vertical. Ver Ejemplo.


