12.4: Ejercicios

Última actualización
Guardar como PDF

Page ID: 111131

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1

Demostrar la identidad

\[ \langle {\mathbf x}, {\mathbf y} \rangle = \frac{1}{2} \left[ \|{\mathbf x} + {\mathbf y}\|^2 - \|{\mathbf x}\|^2 - \| {\mathbf y}\|^2 \right]\text{.} \nonumber \]

2

Demostrar que$O(n)$ es un grupo.

3

Demostrar que las siguientes matrices son ortogonales. ¿Alguna de estas matrices está en$SO(n)\text{?}$

\[ \begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \nonumber \]
\[ \begin{pmatrix} 1 / \sqrt{5} & 2 / \sqrt{5} \\ - 2 /\sqrt{5} & 1/ \sqrt{5} \end{pmatrix} \nonumber \]
\[ \begin{pmatrix} 4/5 & 0 & 3 /5 \\ -3 /5 & 0 & 4 /5 \\ 0 & -1 & 0 \end{pmatrix} \nonumber \]
\[ \begin{pmatrix} 1/3 & 2/3 & - 2/3 \\ - 2/3 & 2/3 & 1/3 \\ 2/3 & 1/3 & 2/3 \end{pmatrix} \nonumber \]

4

Determinar el grupo de simetría de cada una de las figuras de la Figura$12.25$.

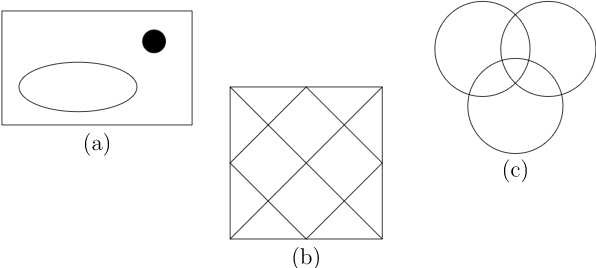
$clipboard_e38819e712a8cd32fcd828b26e9a61036.png$

$Figure 12.25.$

5

Dejar${\mathbf x}\text{,}$${\mathbf y}\text{,}$ y${\mathbf w}$ ser vectores en${\mathbb R}^n$ y$\alpha \in {\mathbb R}\text{.}$ Probar cada una de las siguientes propiedades de los productos internos.

$\langle {\mathbf x}, {\mathbf y} \rangle = \langle {\mathbf y}, {\mathbf x} \rangle\text{.}$
$\langle {\mathbf x}, {\mathbf y} + {\mathbf w} \rangle = \langle {\mathbf x}, {\mathbf y} \rangle + \langle {\mathbf x}, {\mathbf w} \rangle\text{.}$
$\langle \alpha {\mathbf x}, {\mathbf y} \rangle = \langle {\mathbf x}, \alpha {\mathbf y} \rangle = \alpha \langle {\mathbf x}, {\mathbf y} \rangle\text{.}$
$\langle {\mathbf x}, {\mathbf x} \rangle \geq 0$con igualdad exactamente cuando${\mathbf x} = 0\text{.}$
Si$\langle {\mathbf x}, {\mathbf y} \rangle = 0$ para todos${\mathbf x}$ en${\mathbb R}^n\text{,}$ entonces${\mathbf y} = 0\text{.}$

6

Verificar que

\[ E(n) = \{(A, {\mathbf x}) : A \in O(n) \text{ and } {\mathbf x} \in {\mathbb R}^n \} \nonumber \]

es un grupo.

7

Demostrar eso$\{ (2,1), (1,1) \}$ y$\{ ( 12, 5), ( 7, 3) \}$ son bases para una misma celosía.

8

$G$Sea un subgrupo de$E(2)$ y supongamos que$T$ es el subgrupo de traducción de$G\text{.}$ Probar que el grupo puntual de$G$ es isomórfico a$G/T\text{.}$

9

Vamos$A \in SL_2({\mathbb R})$ y supongamos que los vectores${\mathbf x}$ y${\mathbf y}$ forman dos lados de un paralelogramo en${\mathbb R}^2\text{.}$ Probar que el área de este paralelogramo es la misma que el área del paralelogramo con lados$A{\mathbf x}$ y$A{\mathbf y}\text{.}$

10

Demostrar que$SO(n)$ es un subgrupo normal de$O(n)\text{.}$

11

Demuestre que cualquier isometría$f$ en${\mathbb R}^n$ es un mapa uno a uno.

12

Demostrar o desmentir: un elemento en$E(2)$ la forma$(A, {\mathbf x})\text{,}$ donde${\mathbf x} \neq 0\text{,}$ tiene orden infinito.

13

Demostrar o desmentir: Existe un subgrupo abeliano infinito de$O(n)\text{.}$

14

Dejar${\mathbf x} = (x_1, x_2)$ ser un punto en el círculo unitario en${\mathbb R}^2\text{;}$ eso es,$x_1^2 + x_2^2 = 1\text{.}$ Si$A \in O(2)\text{,}$ mostrar que también$A {\mathbf x}$ es un punto en el círculo unitario.

15

Dejar$G$ ser un grupo con un subgrupo$H$ (no necesariamente normal) y un subgrupo normal$N\text{.}$ Entonces$G$ es un producto semidirecto de$N$ por$H$ si

$H \cap N = \{ \identity \}\text{;}$
$HN=G\text{.}$

Demostrar que cada uno de los siguientes es cierto.

$S_3$es el producto semidirecto de$A_3$ por$H = \{(1), (1 \,2) \}\text{.}$
El grupo cuaternión,$Q_8\text{,}$ no puede escribirse como un producto semidirecto.
$E(2)$es el producto semidirecto de$O(2)$ por$H\text{,}$ donde$H$ consta de todas las traducciones en${\mathbb R}^2\text{.}$

16

Determinar cuál de los 17 grupos de papel tapiz conserva la simetría del patrón en la Figura$12.16$.

17

Determinar cuál de los 17 grupos de papel tapiz conserva la simetría del patrón en la Figura$12.26$.

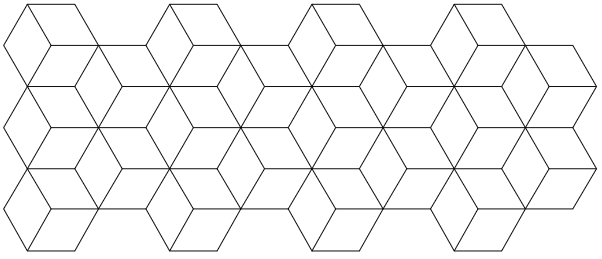
$clipboard_e92e741be277d43abfe72eecd7a4e6adc.png$

$Figure \text { } 12.26.$

18

Encuentra el grupo de rotación de un dodecaedro.

19

Para cada uno de los 17 grupos de papel tapiz, dibuje un patrón de papel tapiz que tenga ese grupo como grupo de simetría.