6.5: Grupos Diedros

Los grupos diedros son grupos de simetrías de\(n\) gones regulares. Empezamos con un ejemplo.

Ejemplo\(\PageIndex{1}\)

Consideremos un triángulo regular\(T\text{,}\) con vértices etiquetados\(1\text{,}\)\(2\text{,}\) y\(3\text{.}\) mostramos\(T\) a continuación, también usando líneas punteadas para indicar una línea vertical de simetría de\(T\) y una rotación de\(T\text{.}\)

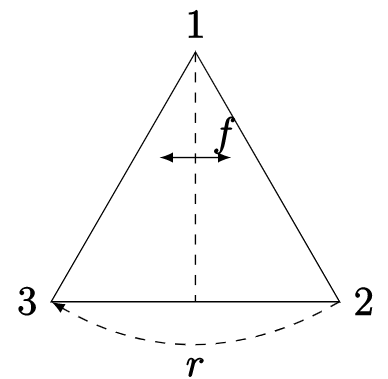
Tenga en cuenta que si reflexionamos\(T\) sobre la línea punteada vertical (indicada en la imagen por\(f\)), se\(T\) mapea sobre sí misma, con\(1\) mapeo hacia\(1\text{,}\)\(2\) y y\(3\) mapeado entre sí. Del mismo modo, si giramos en\(T\) sentido horario\(120^{\circ}\) (indicado en la imagen por\(r\)),\(T\) nuevamente se mapea sobre sí mismo, esta vez con\(1\)\(2\text{,}\)\(2\) mapeo para\(3\) mapear a\(3\text{,}\) y mapear a\(1\text{.}\) Ambos mapas se llaman simetrías de\(T\text{;}\)\(f\) es una reflexión o volteo y\(r\) es una rotación.

Por supuesto, estas no son las únicas simetrías de\(T\text{.}\) Si componemos dos simetrías de\(T\text{,}\) obtenemos una simetría de por\(T\text{:}\) ejemplo, si aplicamos el mapa\(f\circ r\) a\(T\) (significado primero hacer\(r\text{,}\) luego hacer\(f\)) obtenemos reflexión sobre la línea que se conecta\(2\) a el punto medio del segmento de línea\(\overline{13}\text{.}\) Del mismo modo, si aplicamos el mapa\(f\circ (r\circ r)\) a\(T\) (primero hacer\(r\) dos veces, luego hacer\(f\)) obtenemos reflexión sobre la línea\(3\) que conecta con el punto medio del segmento de línea\(\overline{12}\text{.}\) De hecho, cada simetría de se\(T\) puede obtener componiendo aplicaciones de\(f\) y aplicaciones de\(r\text{.}\)

Por conveniencia de la notación, omitimos los símbolos de composición, la escritura, por ejemplo,\(fr\) para\(f\circ r\text{,}\)\(r\circ r\) como\(r^2\text{,}\) etc. Resulta que hay exactamente seis simetrías de\(T\text{,}\) a saber:

1. el mapa\(e\) desde\(T\) hasta el\(T\) envío de cada elemento a sí mismo;
2. \(f\)(es decir, reflexión sobre la línea que conecta\(1\) y el punto medio de\(\overline{23}\));
3. \(r\)(es decir, rotación en sentido horario\(120^{\circ}\));
4. \(r^2\)(es decir, rotación en sentido horario\(240^{\circ}\));
5. \(fr\)(es decir, reflexión sobre la línea que conecta\(2\) y el punto medio de\(\overline{13}\)); y
6. \(fr^2\)(es decir, reflexión sobre la línea que conecta\(3\) y el punto medio de\(\overline{12}\)).

Declarando que\(f^0=r^0=e\text{,}\) el conjunto

\ begin {ecuación*} D_3=\ {e, f, r, r^2, fr, fr^2\} =\ {f^ir^j:i=0,1, j=0,1,2\}\ end {ecuación*}

es la colección de todas las simetrías de\(T\text{.}\)

Observación

Observe eso\(rf=fr^2\) y que\(f^2=r^3=e\text{.}\)

Teorema\(\PageIndex{1}\)

\(D_3\)es un grupo bajo composición.

Prueba

En primer lugar, como se señaló anteriormente,\(rf=fr^2\). Por lo que cualquier mapa del formulario se\(f^ir^jf^kr^l\)\((i,k=0,1,\;\; j,l=0,1,2)\) puede escribir en el formulario\(f^sr^t\) para algunos\(s,t∈N\). Por último, dejemos\(R_2(s)\) y\(R_3(t)\) sean los restos cuando dividas\(s\) por\(2\) y\(t\) por\(3\); entonces\(f^sr^t=f^{R_2(s)}r^{R_3(t)}∈D_3\). Así\(\langle D_3, \circ \rangle\) es una estructura binaria.

A continuación, la composición de la función es siempre asociativa, y la función ee actúa claramente como elemento de identidad en\(D_3\). Por último, vamos\(x=f^ir^j∈D_3\). Entonces\(y=r^{3−j}f^{2−i}\) está en\(D_3\) con\(xy=yx=e\). Así\(D_3\) es un grupo.

En primer lugar, como se señaló anteriormente,\(rf=fr^2\text{.}\) So any map of the form \(f^ir^jf^kr^l\) (\(i,k=0,1\text{,}\) \(j,l=0,1,2\)) can be written in the form \(f^sr^t\) for some \(s,t \in \N\text{.}\) Finally, let \(R_2(s)\) and \(R_3(t)\) be the remainders when you divide \(s\) by \(2\) and \(t\) by \(3\text{;}\) then \(f^sr^t=f^{R_2(s)}r^{R_3(t)} \in D_3\text{.}\) So \(\langle D_3,\circ\rangle \) is a binary structure.

A continuación, la composición de la función es siempre asociativa, y la función\(e\) clearly acts as identity element in \(D_3\text{.}\) Finally, let \(x=f^ir^j\in D_3\text{.}\) Then \(y=r^{3-j}f^{2-i}\) is in \(D_3\) with \(xy=yx=e\text{.}\) So \(D_3\) is a group.

Veamos de\(D_3\) otra manera. Tenga en cuenta que cada mapa en\(D_3\) puede describirse de manera única por cómo permuta los vértices\(1,2,3\) de\(T\text{:}\) eso es, cada mapa en se\(D_3\) puede identificar de manera única con un elemento único de\(S_3\text{.}\) Por ejemplo,\(f\) corresponde a la permutación\((23)\) en\(S_3\text{,}\) while \(fr\)corresponde a la permutación\((13)\text{.}\) En resulta que\(D_3 \simeq S_3\text{,}\) a través de la siguiente correspondencia.

\(e \mapsto e\)

\(f \mapsto (23)\)

\(r \mapsto (123)\)

\(r^2 \mapsto (132)\)

\(fr \mapsto (13)\)

\(fr^2 \mapsto (12)\)

El grupo\(D_3\) es un ejemplo de clase de grupos llamados grupos diedros.

Definición: Grupo Diedro

Dejar\(n\) ser un entero mayor que o igual a\(3\text{.}\) Dejamos\(D_n\) ser la colección de simetrías del\(n\) -gon regular. Resulta que\(D_n\) es un grupo (ver abajo), llamado el grupo diedro de orden\(2n\). (Nota: Algunos libros y matemáticos en cambio denotan el grupo de simetrías del\(n\) -gon regular por\(D_{2n}\) —entonces, por ejemplo, nuestro\(D_3\text{,}\) anterior, en su lugar se llamaría\(D_6\text{.}\) Asegúrese de estar al tanto de la convención que está usando su libro o colega.)

Teorema\(\PageIndex{2}\)

Dejar\(n\) ser un entero mayor que o igual a\(3\text{.}\) Entonces, de nuevo usando la convención que\(f^0=r^0=e\text{,}\)\(D_n\) puede describirse de manera única como

\ begin {ecuación*} d_n=\ {f^ir^j: i=0,1, j=0,1,\ lpuntos, n-1\}\ final {ecuación*}

 

con las relaciones

\ begin {ecuación*} rf=fr^ {n-1}\ texto {y} f^2=r^n=e.\ final {ecuación*}

El grupo diedro grupo\(D_n\) is a nonabeliano de orden\(2n\text{.}\)

Prueba

La prueba de que\(D_n\) es un grupo es paralela a la prueba, arriba, que\(D_3\) es un grupo. Está claro que\(D_n\) es nonabeliano (e.g.,\(rf=fr^{n−1}≠fr\)) y tiene orden\(2n\).

Observación

A lo largo de este curso, si estamos discutiendo un grupo\(D_n\) debe asumir\(n\in \mathbb{Z}^+\text{,}\)\(n\geq 3\text{,}\) a menos que se indique lo contrario.

Definición: Forma estándar

Decimos que un elemento de\(D_n\) está escrito en forma estándar si está escrito en la forma\(f^ir^j\) donde\(i\in \{0,1\}\) y\(j\in \{0,1,\ldots,n-1\}\text{.}\)

Teorema\(\PageIndex{3}\)

Cada uno\(D_n\) es isomórfico a un subgrupo de\(S_n\text{.}\)

Prueba

Presentamos aquí un boceto de una prueba; los detalles se dejan como ejercicio para el lector. Se describió anteriormente cómo\(D_3\) es isomórfico a un subgrupo (es decir, el subgrupo impropio) de\(S_3\). Se puede demostrar que cada uno\(D_n\) es isomórfico a un subgrupo de\(S_n\) etiquetando de manera similar los vértices del\(n\) -gon regular\(1,2,…,n\) y determinando cómo estos vértices son permutados por cada elemento de\(D_n\).

Nota

Si bien en realidad\(D_3\) es isomórfico a\(S_3\) sí mismo, porque\(n>3\) tenemos que no\(D_n\) es isomórfico a\(S_n\) sino que es más bien isomórfico a un subgrupo apropiado de\(S_n\text{.}\) Cuando se\(n>3\) puede ver que\(D_n\) no puede ser isomórfico a\(S_n\) ya que\(|D_n|=2n \lt n! = |S_n|\) para\(n>3\text{.}\)

Es importante poder hacer cálculos con elementos específicos de grupos diedros. Tenemos el siguiente teorema.

Teorema\(\PageIndex{4}\)

Las siguientes relaciones se mantienen\(D_n\text{,}\) en cada\(n\text{:}\)

1. Para cada\(i\text{,}\)\(r^if=fr^{-i}\) (en particular,\(rf=fr^{-1}=fr^{n-1}\));

2. \(o(fr^i)=2\)para cada\(i\) (en particular,\(f^2=e\));

3. \(o(r)=o(r^{-1})=n\text{;}\)

4. Si\(n\) es par, entonces se\(r^{n/2}\) conmuta con cada elemento de\(D_n\text{.}\)

Prueba

 

1. Utilizamos inducción en el exponente de\(r\). Eso ya lo sabemos\(r^1f=fr^{−1}\). Ahora supongamos\(r^{i−1}f=fr^{−(i−1)}\) para algunos\(i≥2\). Entonces

\(r^if=r(r^{i−1}f)=r(fr^{−(i−1)})=(rf)r^{−i+1}=(fr^{−1})r^{−i+1}=fr^{−i}\).

 

2. Por cada\(i\),\(fr^i≠e\), pero

\((fr^i)^2=(fr^i)(fr^i)=f(r^if)r^i=f(fr^{−i})r^i=f^2r^0=e\).

 

3. Esto se deduce del teorema\(5.1.5\) y del hecho de que o (r) =no (r) =n.
4. El comprobante de esta afirmación se deja como ejercicio para el lector.

Ejemplo\(\PageIndex{2}\)

1. Escribir\(fr^2f\)\(D_3\) en forma estándar. Haz lo mismo para\(fr^2f\) en\(D_4\text{.}\)
2. De que es lo inverso\(fr^3\) en\(D_5\text{?}\) Escribirlo en forma estandar.
3. Describir explícitamente un isomorfismo de\(D_4\) a un subgrupo de\(S_4\text{.}\)

Ejemplo\(\PageIndex{3}\)

Clasificar los siguientes grupos hasta isomorfismo. (Pista: Es posible que desee ver el número de elementos de grupo que tienen un orden finito específico).

\ begin {ecuación*}\ mathbb {Z},\ mathbb {Z} _6,\ mathbb {Z} _2, S_6,\ mathbb {Z} _4,\ mathbb {Q}, 3\ mathbb {Z},\ mathbb {R}, S_2,\ mathbb {R} ^*, S_3,\ mathbb {Q} ^*,\ mathbb {C {} ^*,\ langle\ pi\ rangle\ text {in}\ mathbb {R} ^*,\ end {ecuación*}

\ begin {ecuación*} D_6,\ langle (134) (25)\ rangle\ text {in} S_5,\ mathbb {R} ^+, D_3,\ langle r\ rangle\ texto {en} D_4, 17\ mathbb {Z}\ end {ecuación*}