3.4: Geometría elíptica

La geometría elíptica es la geometría de la esfera (la superficie\(2\) -dimensional de una bola sólida\(3\) -dimensional), donde las transformaciones de congruencia son las rotaciones de la esfera alrededor de su centro.

Trabajaremos con tres modelos para geometría elíptica: uno basado en cuaterniones, uno basado en rotaciones de la esfera, y otro que es una subgeometría de geometría de Möbius. Usando la identificación natural\(xi+yj+zk\leftrightarrow (x,y,z)\) de los cuaterniones puros\(\mathbb{R}^3_\mathbb{H}\) con\(\mathbb{R}^3\text{,}\) escribiremos\(S_\mathbb{H}^2\) para denotar el conjunto de cuaterniones puros unitarios.

\[S^2_\mathbb{H}=\{xi+yj+zk\in \mathbb{H}\colon x^2+y^2+z^2=1\}\nonumber \]

Comenzamos por establecer algunos datos básicos sobre los grupos de transformación relevantes.

El grupo de cuaterniones unitarios

Recordemos de la Sección 1.2 que\(U(\mathbb{H})\) es el conjunto de cuaterniones del módulo 1. De hecho,\(U(\mathbb{H})\) es un grupo.

Punto de control 3.4.1.

Demostrar que\(U(\mathbb{H})\) es un grupo.

Recordemos que el mapa\(M\colon \mathbb{H} \to {\mathcal M}_{\mathbb{H}}\) envía\(r=a+bi+cj+dk\) a la matriz

\[\left[\begin{array}{cc} a+bi & c+di\\ -c+di &a-bi\end{array}\right]\text{.}\nonumber \]

La imagen de\(U(\mathbb{H})\) debajo\(M\) es el grupo matriz\(SU(2)\), llamado el grupo unitario especial.

\ begin {ecuación}
SU (2) =\ left\ {\ left [\ begin {array} {cc} a & b\\ -b^\ ast &
a^\ ast\ end {array}\ derecha]\ dos puntos a, b\ in\ mathbb {C},
|a|^2+|b|^2=1\ derecha\}\ etiqueta {su2def}\ tag {3.4.1}
\ end {ecuación}

Restringir el dominio de\(M\) a\(U(\mathbb{H})\) y restringir el codominio de\(M\) to\(M(U(\mathbb{H}))=SU(2)\) es un isomorfismo de grupos

\[U(\mathbb{H})\approx SU(2).\nonumber \]

Punto de control 3.4.2.

Demostrar que\(SU(2)\) es un grupo. Demostrar que\(M\colon U(\mathbb{H})\to SU(2)\) es un homomorfismo.

Pista

No es necesario realizar ningún nuevo cálculo para demostrar que\(M\) es un homomorfismo. En su lugar, use (1.2.5).

La acción de un cuaternión unitario como rotación sobre\(\mathbb{R}^3_\mathbb{H}\) (ver Proposición 1.2.9) toma la esfera\(S^2_\mathbb{H}\) hacia sí misma. La acción del grupo\(U(\mathbf{H})\) en\(S^2_\mathbb{H}\) define un modelo de geometría elíptica.

Definición 3.4.3: modelo cuaternión de geometría elíptica

El modelo de cuaternión de geometría elíptica es\((S^2_\mathbb{H},U(\mathbb{H}))\text{.}\)

Punto de control 3.4.4.

Mostrar que el mapa\ (U (\ mathbb {H})\ a
Perm (S^2_\ mathbb {H})\) dado por

\ [
r\ a\ izquierda [v\ a rvr^\ ast\ derecha]
\ nonumber\]

es una acción grupal.

El grupo de rotaciones de la esfera 2

Dejar\(R_{{v},\theta}\) denotar la rotación de\(\mathbb{R}^3\) alrededor del eje dado por un vector unitario\(v\) por un ángulo\(\theta\text{.}\) Utilizamos la orientación estándar, de manera que un valor positivo de\(\theta\) es una rotación en sentido antihorario del plano ortogonal a\({v}\text{,}\) como se ve desde “arriba” donde\(v\) apunta en la dirección “arriba”. Ver Figura 3.4.5.

Figura 3.4.5. La rotación\(R_{v,\theta}\) alrededor del vector\(v\) por el ángulo\(\theta\)

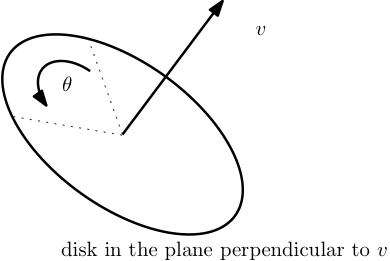
Convención de notación: Por legibilidad y conveniencia, escribimos\(R_{X,\theta},R_{Y,\theta},R_{Z,\theta}\) para denotar rotaciones por\(\theta\) radianes sobre los vectores base estándar\((1,0,0), (0,1,0), (0,0,1)\text{,}\) respectivamente.

Escribiremos\(Rot(S^2)\) para denotar el conjunto de todas las rotaciones.

\ [
Rot (S^2) =\ {R_ {{v},\ theta}\ colon
{v}\ in\ mathbb {R} ^3, | {v} |=1,\ theta\ in\ mathbb {R}\}
\ nonumber\]

Para ver por qué el conjunto\(Rot(S^2)\) es un grupo ¹ bajo la operación de composición, considere el mapa\(U(\mathbb{H})\to Rot(S^2)\) dado por\(r\to R_r\) establecido por la Proposición 1.2.9. El hecho de que\(R_r\circ R_s = R_{rs}\) (ver Ejercicio 1.2.6.3) implica que la composición de dos rotaciones es una rotación. Las propiedades restantes del grupo son sencillas. Una vez que hemos probado que\(Rot(S^2)\) es un grupo, la misma ecuación\(R_r\circ R_s = R_{rs}\) muestra que el mapa\(r\to R_r\) es un homomorfismo de grupos\(U(\mathbb{H})\to Rot(S^2)\text{.}\) El núcleo de este homomorfismo es\(\{\pm 1\}\text{.}\) Esto establece un isomorfismo

\ [
U (\ mathbb {H})/\ {\ pm 1\}\ approx Rot (S^2).
\ nonumber\]

Punto de control 3.4.6.

Completa los detalles para demostrar que\(Rot(S^2)\) es un grupo. Mostrar que el núcleo del homomorfismo\(U(\mathbb{H})\to Rot(S^2)\) dado por\ (r\ a
R_r\) es\(\{\pm 1\}\text{.}\)

Pista

Utilice la Proposición 1.2.9.

Definición 3.4.7.

El modelo esférico de geometría elíptica es\((S^2,Rot(S^2))\text{.}\)

Concluimos con un dato útil sobre la construcción de rotaciones arbitrarias mediante la composición de rotaciones a partir de un conjunto específico de tipos elementales, es decir, rotaciones alrededor del eje z por ángulos arbitrarios y rotaciones alrededor del\(x\) eje por\(\pi/2\) radianes. Comenzamos con un Lema que muestra cómo hacer esto para rotaciones de\(y\) ejes.

Lema 3.4.8. Rotaciones sobre el\(y\)-axis.

Una rotación arbitraria alrededor del\(y\) eje es una composición de rotaciones alrededor del\(x\) eje por\(\pi/2\) radianes con una rotación alrededor del\(z\) eje. En concreto, tenemos lo siguiente.

\ begin {ecuación}
R_ {Y,\ theta} = R_ {X,\ pi/2} ^ {-1}\ circ R_ {Z,\ theta}\ circ R_ {X,\ pi/2}\ etiqueta {yrotdecomp}\ etiqueta {3.4.2}
\ final {ecuación}

Prueba.

¡Visualiza! También se puede verificar comprobando que ambos lados de (3.4.2) arrojan el mismo resultado cuando se evalúan sobre los tres vectores de base estándar. Otra prueba más es hacer un cómputo cuaternión.

Proposición 3.4.9. Generadores para\(Rot(S^2)\)

El conjunto

\ [
\ {R_ {Z,\ theta}\ colon\ theta\ in
\ mathbb {R}\}\ copa\ {R_ {X,\ pi/2}\}
\ nonumber\]

es un conjunto generador para\(Rot(S^2)\text{.}\) Esto significa que cualquier rotación puede escribirse como una composición de rotaciones alrededor del\(z\) eje y rotaciones alrededor del\(x\) eje por\(\pi/2\) radianes.

Prueba.

Considera un modelo de la esfera impreso con un mapa del mundo (es decir, un globo geográfico) de tal manera que el polo norte esté encima de la esfera y Greenwich, Inglaterra (a cero grados de longitud) esté en el\(x,z\) plano. La esfera en la parte superior izquierda de la Figura 3.4.10 representa esta posición de “inicio” del polo norte de\(N\text{,}\) Greenwich\(G\text{,}\) y el gran círculo\(C\) que es la intersección de la esfera con el\(x,z\) plano (\(C\)se muestra en rojo en las cuatro esferas para referencia). Ahora dejemos\(R\) ser una rotación arbitraria. La esfera en la parte superior derecha de la Figura 3.4.10 muestra cómo\(N\text{,}\)\(G\text{,}\) y\(C\) son transformados por\(R\text{.}\) El resto del diagrama muestra cómo podemos escribir\(R^{-1}\) como una composición de rotaciones “poniendo el polo norte de nuevo en la parte superior” y “volviendo a poner cero grados en lugar”, de la siguiente manera. Desde la parte superior derecha en el diagrama, “volvemos a poner el polo norte” realizando primero una rotación\(R_{Z,\theta_1}\) alrededor del\(z\) eje -eje que lleva al polo norte al\(x,z\) plano. A continuación, realizamos la rotación\(R_{Y,\theta_2}\) alrededor del\(y\) eje -eje (usamos el Lema) para llevar el polo norte de nuevo a la cima. Finalmente, realizamos una rotación\(R_{Z,\theta_3}\) para traer Greenwich de vuelta a casa en el\(x,z\) avión. Lectura en sentido horario desde la parte superior izquierda del diagrama, la secuencia de transformaciones

\ [
R, R_ {Z,\ theta_1}, R_ {Y,\ theta_2}, R_ {Z,\ theta_3}
\ nonumber\]

toma el polo norte\(N\) a través de la secuencia

\ [
N\ a R (N)\ a N'\ a N"=N\ a N\ texto {.}
\ nonumber\]

En tanto,\(G\) traza el camino

\ [
G\ a R (G)\ a
G'\ a G "\ a G
\ no número\]

mientras que el gran círculo\(C\) se transforma en la secuencia

\ [
C\ a R (C)\ a C'\ a C "\ a C.
\ nonumber\]

Esto lleva a la descomposición\(R=R_{Z,-\theta_1}\circ R_{Y,-\theta_2}\circ R_{Z,-\theta_3}\text{.}\)

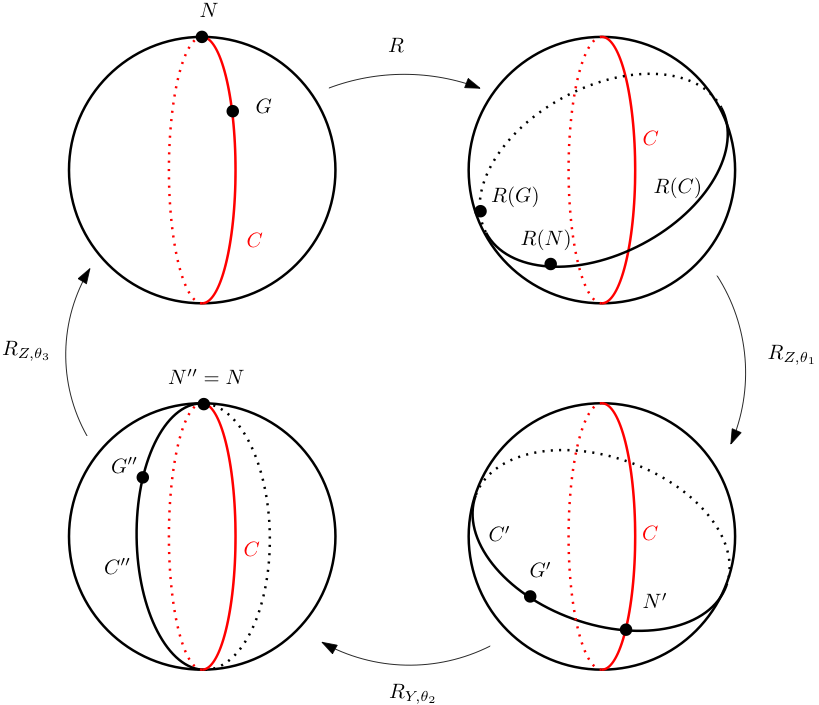
Figura 3.4.10. Descomposición de la rotación\(R\)

El subgrupo elíptico del grupo Möbius

Vamos a\(\mathbf{S}\) denotar el grupo de transformaciones de las\(\hat{\mathbb{C}}\) que se conjugan con rotaciones de\(S^2\) vía la proyección estereográfica.

\ [
\ mathbf {S} =\ {s\ circ R\ circ s^ {-1}\;\;\;\ dos puntos\;\; R\ en
Rot (S^2)\}
\ nonumber\]

El grupo\(\mathbf{S}\S is called the elliptic group. It is easy to check that the map \(Rot(S^2)\to \mathbf{S}\) dado por\(R\to s\circ R\circ s^{-1}\) es un isomorfismo de grupos, así que tenemos

\ [
\ mathbf {S}\ approx Rot (S^2).
\ nonumber\]

Punto de control 3.4.11.

Demostrar que efectivamente\(\mathbf{S}\) es un grupo. Demostrar que\(R\to s\circ R\circ s^{-1}\) es un isomorfismo grupal\(Rot(S^2)\to \mathbf{S}\text{.}\)

Los ejercicios de la Sección 1.3 muestran que\(s\circ R_{Z,\theta}\circ s^{-1}\) la transformación de Möbius\(T_{Z,\theta}\) dada por\(z\to e^{i\theta}z\) (ver Ejercicio 1.3.3.4) y que\(s\circ R_{X,\pi/2}\circ s^{-1}\) es la transformación de Möbius\(T_{X,\pi/2}\) dada por\(z\to \frac{z+i}{iz+1}\) (ver Ejercicio 1.3.3.6). El hecho (Proposición 3.4.9) que las rotaciones de la forma\(R_{Z,\theta},R_{X,\pi/2}\) generan\(Rot(S^2)\) implica que las transformaciones de Möbius\(T_{Z,\theta}\) y\(T_{X,\pi/2}\) generan\(\mathbf{S}\). Por lo tanto,\(\mathbf{S}\) es de hecho un subgrupo del grupo Möbius.

Definición 3.4.12.

El modelo de subgeometría Möbius de geometría elíptica es\((\hat{\mathbb{C}},\mathbf{S})\text{.}\)

Podemos decir más sobre la forma específica de los elementos\(\mathbf{S}\) en términos del grupo homomorfismo\ ({\ mathcal
T}\ colon GL (2,\ mathbb {C})\ to\ mathbf {M}\) que envía la matriz\ (\ left [\ begin {array} {cc} a & b\\ c &
d\ end {array}\ right]\) a la transformación de Möbius \(z\to \frac{az+b}{cz+d}\)(véase (3.2.2)). Observe que las transformaciones

\ begin {align}
T_ {Z,\ theta} & = {\ mathcal T}\ left (\ left [\ begin {array} {cc}
e^ {i\ theta/2} & 0\\ 0 &
e^ {-i\ theta/2}\ end {array}\ derecha]\ derecha)\ label {tzthetaassu2image}\ tag {3.4.3}\
T_ {X,\ pi/2} & = {\ mathcal T}\ left (\ left [\ begin {array} {cc}
\ frac {1} {\ sqrt {2}} &\ frac {i} {\ sqrt {2}}\
\ frac {i} {\ sqrt {2}} &\ frac {1} {\ sqrt {2}}\ end {array}\ derecha]\ right)\ label {txpiby2assu2image}\ tag {3.4.4}
\ end {align}

son imágenes de elementos del grupo\(SU(2)\) (ver (3.4.1)). Porque\(T_{Z,\theta},T_{X,\pi/2}\) generar\(\mathbf{S}\), se deduce que cada elemento de\(\mathbf{S}\) es la imagen bajo\({\mathcal T}\) de un elemento de\(SU(2)\text{.}\)

Punto de control 3.4.13.

Dejar\(M_{Z,\theta},M_{X,\pi/2}\) denotar las matrices\ (\ left [\ begin {array} {cc}
e^ {i\ theta/2} & 0\\ 0 &
e^ {-i\ theta/2}\ end {array}\ right],\ left [\ begin {array} {cc}
\ frac {1} {\ sqrt {2}} &\ frac {i} {\ sqrt {2}}\\
\ frac {i} {\ sqrt {2}} &\ frac {1} {\ sqrt {2 }}\ end {array}\ right]\) respectivamente. Verificar que efectivamente\(M_{Z,\theta},M_{X,\pi/2}\) son elementos de\(SU(2)\text{.}\) Verify (3.4.3) y (3.4.4). Explique el comentario final en el párrafo anterior. ¿Por qué se deduce que cada elemento de\(\mathbf{S}\) es la imagen de un elemento de\(SU(2)\text{?}\)

Así, hemos demostrado la siguiente fórmula explícita para los elementos de\(\mathbf{S}\)

Proposición 3.4.14. Fórmula para transformaciones en el grupo elíptico.

Un mapa\(T\) es un elemento de\(\mathbf{S}\) si y solo si se\(T\) puede escribir en la forma\(Tz=\frac{az+b}{-b^\ast z+a^\ast}\) para algunos\(a,b\in \mathbb{C}\) con\(|a|^2+|b|^2=1\text{.}\)

Configuración\(e^{i\theta}=\frac{a}{a^\ast}\) y\(z_0=\frac{-b}{a}\text{,}\) tenemos la siguiente forma alternativa para\(T\in \mathbf{S}\text{.}\)

\ begin {ecuación}
tz=e^ {i\ theta}\ frac {z-z_0} {z_0^\ ast z+1}\ label {elípticgp0inftyform}\ tag {3.4.5}
\ end {ecuación}

Círculos en S^2 y clinos en C^

Un círculo en\(S^2\) es un círculo en un plano que se cruza\(S^2\text{.}\) Un gran círculo es la intersección de\(S^2\) con un plano a través del origen. En geometría elíptica, un gran círculo se llama línea recta elíptica porque el camino de menor longitud que conecta dos puntos dados en\(S^2\) es un arco de un gran círculo. Los círculos en\(S^2\) que no son grandes círculos se llaman ciclos elípticos. Las líneas rectas elípticas y los ciclos elípticos en el modelo de subgeometría de Möbius\((\hat{\mathbb{C}},\mathbf{S})\) son proyecciones estereográficas de líneas rectas elípticas y ciclos elípticos en el modelo esférico. Resulta que las líneas rectas elípticas y los ciclos elípticos en\(\hat{\mathbb{C}}\) son de hecho clines. Aquí está la declaración y la prueba.

Proposición 3.4.15. La proyección estereográfica lleva los círculos a los clines.

Dejar\(C\) ser un círculo que es la intersección de\(S^2\) con un plano en\(\mathbb{R}^3\text{.}\) Si\(C\) contiene el polo norte\((0,0,1)\) de\(S^2\text{,}\) entonces\(s(C\setminus\{(0,0,1)\})\) es una línea recta euclidiana en\(\mathbb{C}\text{.}\) De lo contrario,\(s(C)\) es un círculo en\(\mathbb{C}\).

Prueba.

Croquis de prueba: La declaración sobre el caso cuando\(C\) contiene el polo norte es geométricamente clara. Para el caso cuando\(C\) no contiene\((0,0,1)\text{,}\) elegir una rotación\(R\) de\(S^2\) que lleve algún punto sobre\(C\) el polo norte. Nuevamente, deja\(T=s\circ R\circ s^{-1}\) ser el elemento conjugado en\(\mathbf{S}\text{.}\) Está claro que\(R\) lleva\(C\) a un círculo, eso s lleva\(R(C)\) a una línea recta euclidiana, y eso\(T^{-1}\) lleva\(s(R(C))\) a una clina (porque\(T^{-1}\) es una transformación de Möbius!). Así\(s(C)=(T^{-1}\circ s\circ R)(C)\) es un cline. Porque no\((0,0,1)\) está en\(C\text{,}\) él debe ser que no\(\infty\) está encendido\(s(C)\text{,}\) así\(s(C)\) es un círculo en\(\mathbb{C}\text{.}\)

Ángulos y orientación en S^2

La orientación estándar para los ángulos en\(S^2\) (ver Subsección 3.4.2) también se denomina orientación normal que apunta hacia afuera. La orientación estándar mide ángulos desde el punto de vista de un observador parado en el exterior de la esfera. La orientación normal que apunta hacia adentro es la orientación inversa que mide los ángulos desde el punto de vista de un observador que camina por el interior de la esfera. Ver Figura 3.4.16.

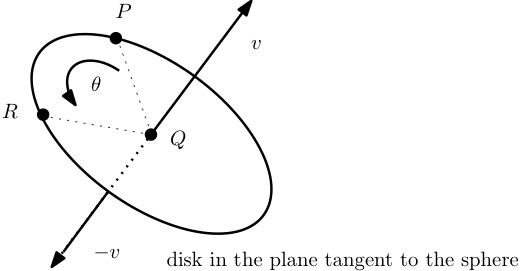
Figura 3.4.16. Dos orientaciones en la esfera: el ángulo orientado\ (\ ángulo
PQR\) es positivo visto desde el vector normal que apunta hacia afuera\(v\text{,}\), pero es negativo visto desde el vector que apunta hacia adentro\(-v\text{.}\)

Corolario 3.4.17. La proyección estereográfica es conforme.

La proyección estereográfica conserva los ángulos orientados con respecto a la orientación normal que apunta hacia adentro.

Prueba.

Croquis de prueba: Comienza con el caso especial de curvas\(C_1,C_2\) que se cruzan en el polo sur\(S=(0,0,-1)\text{.}\) Las líneas\(L_1,L_2\) que son tangentes a\(C_1,C_2\) en\(S\) yacen en planos\(\Pi_1,\Pi_2\) que contienen el polo sur y el origen. Las tangentes\(L_1,L_2\) también se encuentran en el plano\(z=-1\) tangente a la esfera en el polo sur. Es claro que las líneas\(L_1',L_2'\) tangentes a\(s(C_1),s(C_2)\) at\(s(S)=0\) son líneas rectas que se cruzan en el origen. ¡El ángulo hecho por\(L_1,L_2\) es el mismo que el ángulo hecho por los planos\(\Pi_1,\Pi_2\text{,}\) pero con orientación hacia dentro de lo normal! Ver Figura 3.4.18. Ahora supongamos que dos curvas se cruzan en\(P\text{.}\) Elige una rotación\(R\) de\(S^2\) que lleva\(P\) al polo sur, y deja\(T=s\circ R\circ s^{-1}\) ser el elemento conjugado en\(\S\text{.}\) Es claro que\(R\) y\(T\) son conformes (porque\(T\) es una transformación de Möbius!). Ahora bien, el hecho de que\(s\) sea conforme a\((0,0,-1)\) implica que\ (s=t^ {-1}\ circ s\ circ
R\) es conforme en\(P\text{.}\)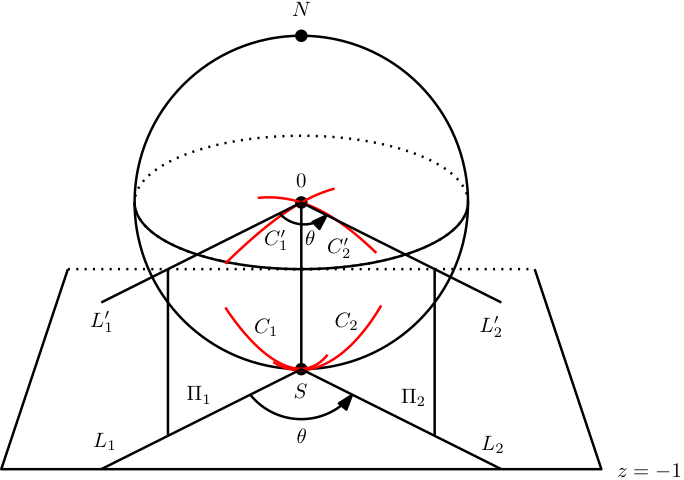

Figura 3.4.18. La proyección estereográfica es conforme a\(S=(0,0,-1)\text{.}\)

Longitud y área elíptica

La distancia entre puntos\(S^2\) es\(P,Q\) la longitud del arco de un gran círculo que los conecta. Debido a que la esfera tiene radio\(1\), la longitud del arco es la misma que la medida del radián del ángulo\(\angle POQ\text{,}\) donde\(O\) está el origen. A partir del cálculo vectorial, tenemos la siguiente fórmula de producto punto.

\ [
(\ overrightarrow {OP})\ cdot (\ overrighttarrow {OQ}) =|\ overrightarrow {OP} ||\ overrighttarrow {OQ} |\ cos (\ ángulo
POQ)
\ nonumber\]

Resolviendo para\(\cos(\angle POQ)\text{,}\) obtenemos la fórmula para la distancia\(d_{S^2}(P,Q)\) entre puntos\(P,Q\) en\(S^2\text{.}\)

\ begin {ecuación}
d_ {S^2} (P, Q) =\ cos^ {-1}\ izquierda ((\ overrightarrow {OP})\ cdot (\ overrighttarrow {OQ})\ derecha)\ label {s2metric}\ tag {3.4.6}
\ end {ecuación}

“Transferir” la métrica (3.4.6) a\(\hat{\mathbb{C}}\) por proyección estereográfica significa que definimos la métrica\(d_{\hat{\mathbb{C}}}\) elíptica\(\hat{\mathbb{C}}\) por lo siguiente.

\ begin {ecuación}
d_ {\ hat {\ mathbb {C}}} (p, q) :=d_ {S^2} (s^ {-1} (p), s^ {-1} (q))\ label {eliptic_metric_def}\ tag {3.4.7}
\ end {ecuación}

Proposición 3.4.19.

La métrica elíptica (3.4.7) es invariante bajo la acción del grupo elíptico. Es decir, tenemos

\ begin {ecuación}
d_ {\ hat {\ mathbb {C}}} (p, q) = d_ {\ hat {\ mathbb {C}}} (Tp, Tq)\ tag {3.4.8}
\ end {ecuación}

para todos\(p,q\in \hat{\mathbb{C}}\) y para todos\(T\in \mathbf{S}\text{.}\)

Prueba.

Ver Ejercicio 3.4.7.2.

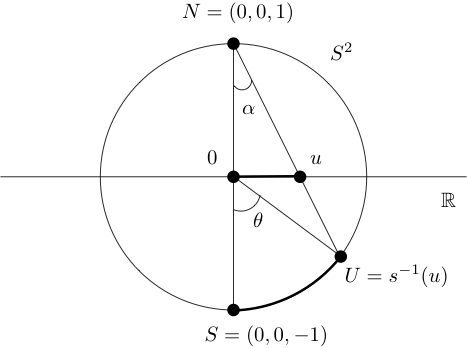
Para obtener una fórmula para la computación\(d_{\hat{\mathbb{C}}}(p,q)\text{,}\) seguimos el mismo procedimiento para la distancia hiperbólica. En primer lugar, encontramos la distancia\(d_{\hat{\mathbb{C}}}(0,u)\text{,}\) donde\ (0\ leq u\ leq
1\ text {.}\) Let et\(U=s^{-1}(u)\text{.}\) let\(0=(0,0,0)\text{,}\) let\(N=(0,0,1)\text{,}\) let\ (\ alpha =
\ angle SNU\) y let\(\theta = \angle SOU\) (ver Figura 3.4.20).\(S=(0,0,-1)=s^{-1}(0)\) Es un ejercicio sencillo para demostrar\(\alpha = \theta/2\text{,}\) que para que tengamos

\ begin {ecuación}
d_ {\ hat {\ mathbb {C}}} (0, u) =d_ {S^2} (S, U) =\ theta = 2\ alpha=2\ arctan u.\ etiqueta {elipticdist0u}\ tag {3.4.9}
\ end {ecuación}

 

Figura 3.4.20. Transferir la métrica natural\(S^2\) a\(\hat{\mathbb{C}}\) mediante proyección estereográfica.

Punto de control 3.4.21.

\(\theta/2=\alpha=\arctan u\)Demuéstralo en la Figura 3.4.20.

Para el caso general, let\(z_1,z_2\in \hat{\mathbb{C}}\text{.}\) Because y let\(Tz=e^{it}\frac{z-z_1}{z_1^\ast z+1}\) be la transformación in\(\mathbf{S}\) (usando la forma (3.4.5)) que envía\(z_1\to 0\) y\(z_2\to u\geq 0\text{.}\) Aplicando (3.4.9), tenemos la fórmula de distancia elíptica en\(\hat{\mathbb{C}\text{.}\)

\ begin {ecuación}
d_ {\ hat {\ mathbb {C}}} (z_1, z_2) =2\ arctan
\ izquierda|\ frac {z_2-z_1} {z_1^\ ast z_2 + 1}\ derecha|\ label {elipticdist}\ tag {3.4.10}
\ end {ecuación}

Ahora vamos a\(\gamma\) ser una curva paramétrica\(z(t)=x(t)+iy(t)\) adentro\(\hat{\mathbb{C}}\). Usando el mismo argumento que en el párrafo anterior a la fórmula integral de longitud hiperbólica (3.3.6), usando la aproximación de Taylor de primer orden\(\arctan u \approx u\) y realizando los cambios apropiados, llegamos a la fórmula integral de longitud elíptica.

\ begin {ecuación}
\ texto {Longitud} (\ gamma) =2\ int_a^b\ frac {|z' (t) |} {1+|z (t) |^2}\; dt\ label {elípticlongitudfórmula}\ tag {3.4.11}
\ end {ecuación}

Punto de control 3.4.22.

Mostrar que la aproximación de Taylor de primer orden para\(\arctan u\) es\(u\text{.}\) Completar los detalles de modificación de la derivación de la fórmula integral de longitud hiperbólica para obtener la fórmula integral de longitud elíptica.

Punto de control 3.4.23.

Encuentra la longitud del ciclo elíptico parametrizada\(z(t) = \alpha e^{it}\) por\(0\leq t\leq 2\pi\text{,}\) dónde\(0\lt \alpha\leq 1\)

Usando el mismo argumento que en el párrafo anterior a la fórmula integral de área hiperbólica (3.3.10), usando el diferencial de longitud elíptica\(ds=\frac{2|z'(t)|\;dt}{1-|z(t)|^2}\) en lugar del diferencial de longitud hiperbólica y realizando los cambios apropiados, obtenemos la fórmula integral de área elíptica.

\ begin {ecuación}
\ texto {Área} (R) =\ iint_r
dA =\ iint_r\ frac {4r\; dr\; d\ theta} {(1+r^2) ^2}. \ label {ellipticareaintformula}\ tag {3.4.12}
\ end {ecuación}

Punto de control 3.4.24.

Encuentra el área del disco elíptico\ (\ {|z|\ leq
\ alpha\}\ text {,}\) para\(0\lt \alpha\lt 1\text{.}\)

Ejercicios

Ejercicio 1

Mostrar que los tres modelos de geometría elíptica son equivalentes.

Ejercicio 2

Proponer Proposición 3.4.19

Área de un triángulo elíptico.

La siguiente secuencia de ejercicios establece la fórmula de área para triángulos elípticos.

Ejercicio 3

Área de una elíptica de 2 gones.

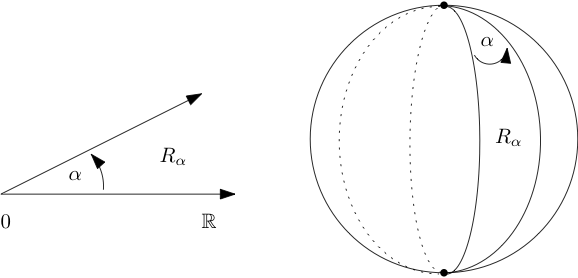
Un \(2\)-gon elíptico es una figura con dos vértices conectados por dos segmentos de línea elíptica. En\(\hat{\mathbb{C}}\), cualquier\(2\) -gon es congruente con un conjunto de la forma\(R_{\alpha} :=\{z\in \mathbb{C}\colon 0\leq \arg z \leq \alpha\}\cup \{\infty\}\) para algunos\(\alpha\) en el rango\ (0\ leq\ alpha\ lt
2\ pi\ text {.}\) Ver Figura 3.4.25. Use un área integral en\(\hat{\mathbb{C}}\) para mostrar que el área de\(R_{\alpha}\) es\(2\alpha\text{.}\) Verifique que esta sea la respuesta correcta usando una imagen de\(S^2\text{.}\)

Figura 3.4.25. \(2\)-gons en\(\hat{\mathbb{C}}\) y\(S^2\text{.}\)

Ejercicio 4

Área de un triángulo elíptico.

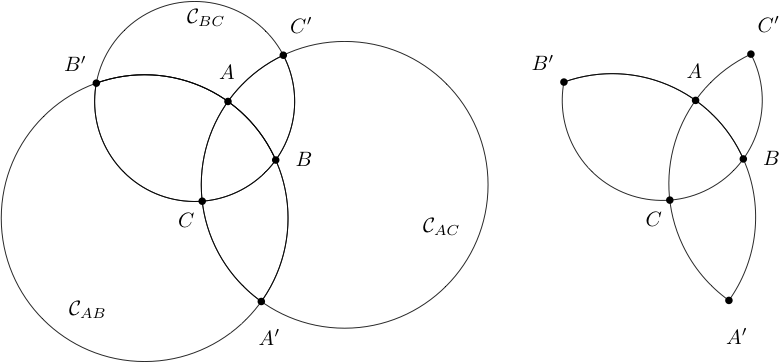
Dejar\(\triangle ABC\) ser un triángulo elíptico. Que\ ({\ mathcal C} _ _ {AB}, {\ mathcal
C} _ {AC}, {\ mathcal C} _ _ {BC}\) denoten los grandes círculos que extienden los lados\(AB,AC,BC\) del triángulo. Ver Figura 3.4.26.

1. Explique por qué\(A,A'\) son puntos finales del mismo diámetro, es decir, puntos finales de un diámetro de\(S^2\) o sus proyecciones estereográficas en\(\hat{\mathbb{C}}\).
2. ¡Explique por qué\(\triangle A'B'C'\) tiene la misma área que\(\triangle ABC\text{,}\) aunque los dos triángulos no sean necesariamente congruentes! (Tenga en cuenta que el interior de\(\triangle A'B'C'\) es el exterior de los tres grandes círculos, es decir, en el lado que contiene el punto\(\infty\text{.}\)) Insinuación: ¿Qué implica la parte (a) de este problema sobre la relación entre puntos\(X\) y\(X'\) sobre\(S^2\) para\(X=A,B,C\text{?}\)
3. Vamos a\(R\) denotar el interior de la región que se muestra en la figura de la derecha en la figura 3.4.26. Explicar por qué el área de\(R\) es

   \ [
   2\ ángulo A + 2\ ángulo B + 2\ ángulo C - 2\ texto {Área} (\ triángulo
   ABC).
   \ nonumber\]

   Sugerencia: Descomponer\(R\) usando\(\) 2 gones superpuestos.
4. Vamos a\(R'\) denotar el exterior de la región es\(R\text{,}\) decir,\(R'=\hat{\mathbb{C}}\setminus R\text{.}\) explicar por qué la zona de\(R'\) es

   \ [
   2\ ángulo A + 2\ ángulo B + 2\ ángulo C - 2\ texto {Área} (\ triángulo
   A'B'C').
   \ nonumber\]

   Sugerencia: Descomponerse\(R'\) en\(2\) -gones superpuestos.
5. Explica por qué el área del triángulo elíptico\(\triangle ABC\) es

   \ begin {ecuación}
   \ texto {Área} (\ triángulo
   ABC) = (\ ángulo A +\ ángulo B +\ ángulo
   C) -\ pi. \ label {eliptictrianglearea}\ tag {3.4.13}
   \ end {ecuación}

Figura 3.4.26.