5.1: Cosets
- Page ID
- 117768
Sin lugar a dudas, has notado en numerosas ocasiones que si\(G\) es un grupo con\(H\leq G\) y\(g\in G\), luego ambos\(|H|\) y se\(|g|\) dividen\(|G|\). El teorema que dice que esto es siempre el caso se llama teorema de Lagrange y lo demostraremos hacia el final de este capítulo. Comenzamos con una definición.
Seamos\(G\) un grupo y dejemos\(H\leq G\) y\(a\in G\). Los subconjuntos\[aH:=\{ah\mid h\in H\}\] y\[Ha:=\{ha\mid h\in H\}\] se denominan los coconjuntos izquierdo y derecho de\(H\) contener\(a\), respectivamente.
Para obtener una idea, juguemos con un ejemplo. Considera el grupo diedro\(D_3=\langle r,s\rangle\) y deja\(H=\langle s\rangle\leq D_3\). Para calcular los coconjuntos correctos de\(H\), necesitamos multiplicar todos los elementos de a\(H\) la derecha por los elementos de\(G\). Vemos eso\[\begin{aligned} & He =\{ee,se\}=\{e,s\}=H\\ & Hr=\{er,sr\}=\{r,sr\}\\ & Hr^2=\{er^2,sr^2\}=\{r^2,rs\}\\ & Hs=\{es,ss\}=\{s,e\}=H\\ & Hsr=\{esr,ssr\}=\{sr,r\}\\ & Hrs=\{ers,srs\}=\{rs,ssr^2\}=\{rs,r^2\}.\end{aligned}\] A pesar de que hicimos seis cálculos (uno por cada elemento en\(D_3\)), si escaneamos la lista, vemos que solo hay 3 cosets distintos, a saber\[\begin{aligned} & H=He=Hs=\{e,s\}\\ & Hr=Hsr=\{r,sr\}\\ & Hr^2=Hrs=\{r^2,rs\}.\end{aligned}\] Podemos hacer algunas observaciones más. Primero, los cosets resultantes formaron una partición de\(D_3\). Es decir, cada elemento de\(D_3\) aparece exactamente en un coset. Además, todos los cosets son del mismo tamaño, dos elementos en cada coset en este caso. Por último, cada coset puede ser nombrado de múltiples maneras. En particular, los elementos del coset son exactamente los elementos de\(D_3\) nosotros multiplicados\(H\) por. Por ejemplo,\(Hr=Hsr\) y los elementos de este coset son\(r\) y\(sr\). A la brevedad, veremos que estas observaciones se mantienen, en general.
Aquí hay otra observación significativa que podemos hacer. Considere el diagrama de Cayley para\(D_3\) con grupo generador\(\{r,s\}\) que se da en la Figura\(\PageIndex{1}\). Dado este diagrama de Cayley, podemos visualizar el subgrupo\(H\) y sus clones. Además,\(H\) y sus clones son exactamente los 3 coconjuntos correctos de\(H\). Veremos que, en general, los coconjuntos correctos de un subgrupo dado son siempre el subgrupo y sus clones (ver Problema\(\PageIndex{7}\)).
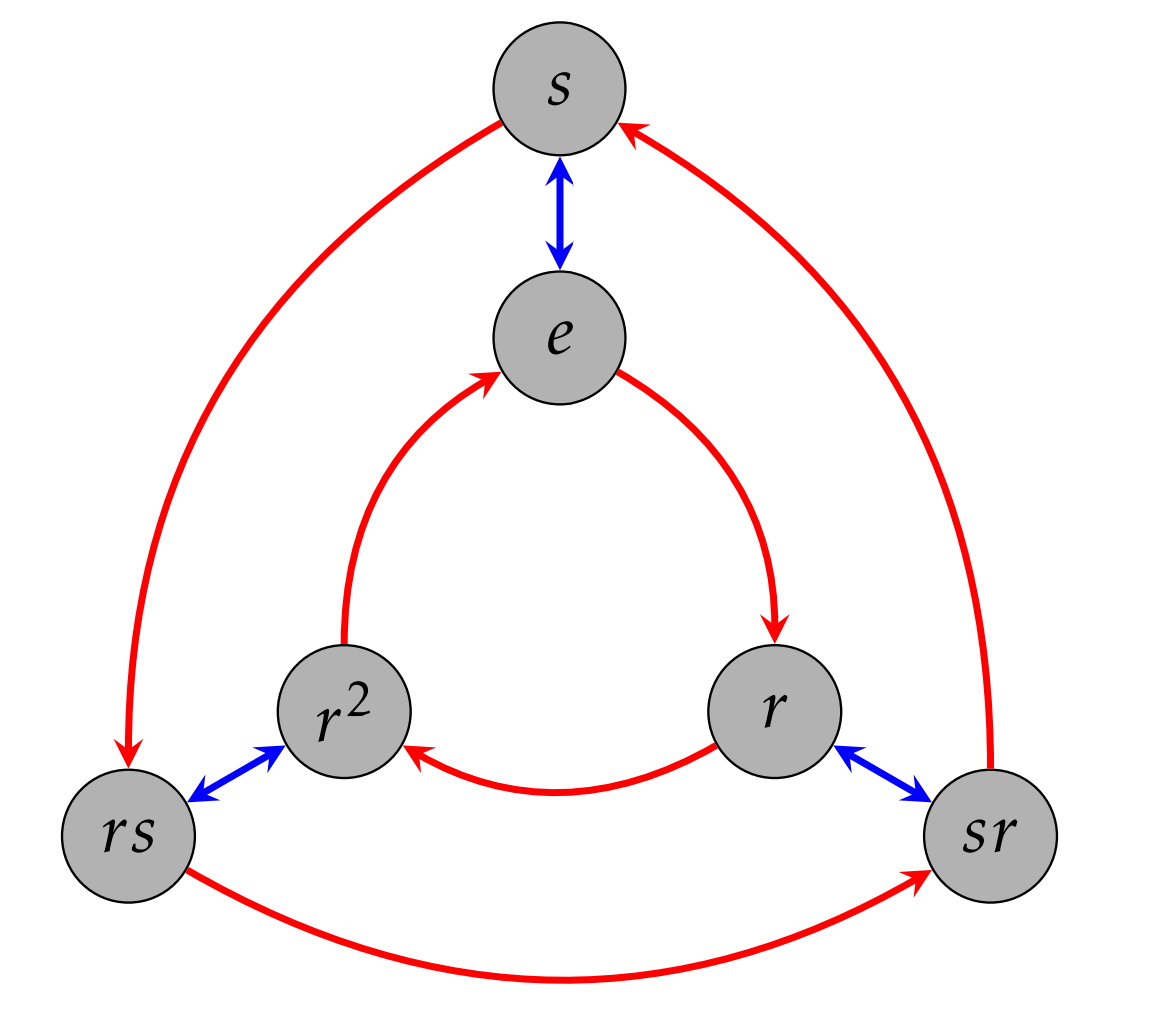
Considera al grupo\(D_3\). Encuentra todos los cosets de la izquierda para\(H=\langle s\rangle\). ¿Son lo mismo que los cosets adecuados? ¿Son lo mismo que el subgrupo\(H\) y sus clones que podemos ver en la gráfica Cayley para\(D_3\) con grupo generador\(\{r,s\}\)?
Como indica el ejercicio anterior, las colecciones de coconjuntos izquierdo y derecho pueden no ser las mismas y cuando no son iguales, el subgrupo y sus clones no coinciden con los coconjuntos izquierdos.
Podrías estar pensando que de alguna manera los cosets derechos son “mejores” que los cosets izquierdos ya que pudimos visualizarlos en la gráfica de Cayley. No obstante, esto es solo una consecuencia de nuestra convención de componer acciones de derecha a izquierda. Si hubiéramos adoptado una convención de izquierda a derecha, entonces podríamos visualizar los cosets izquierdos en diagramas de Cayley.
Computar los cosets izquierdo y derecho usando una tabla de grupo es bastante fácil. Ojalá, te diste cuenta en Problema\(\PageIndex{1}\) que los cosets izquierdos de\(H=\langle s\rangle\) in\(D_3\) son\(H=\{e,s\}\),\(srH=\{r^2,sr\}\), y\(rsH=\{r,rs\}\). Ahora, considere la siguiente tabla de grupo para\(D_3\) que tenga las filas y columnas dispuestas de acuerdo con los cosets izquierdos de\(H\).
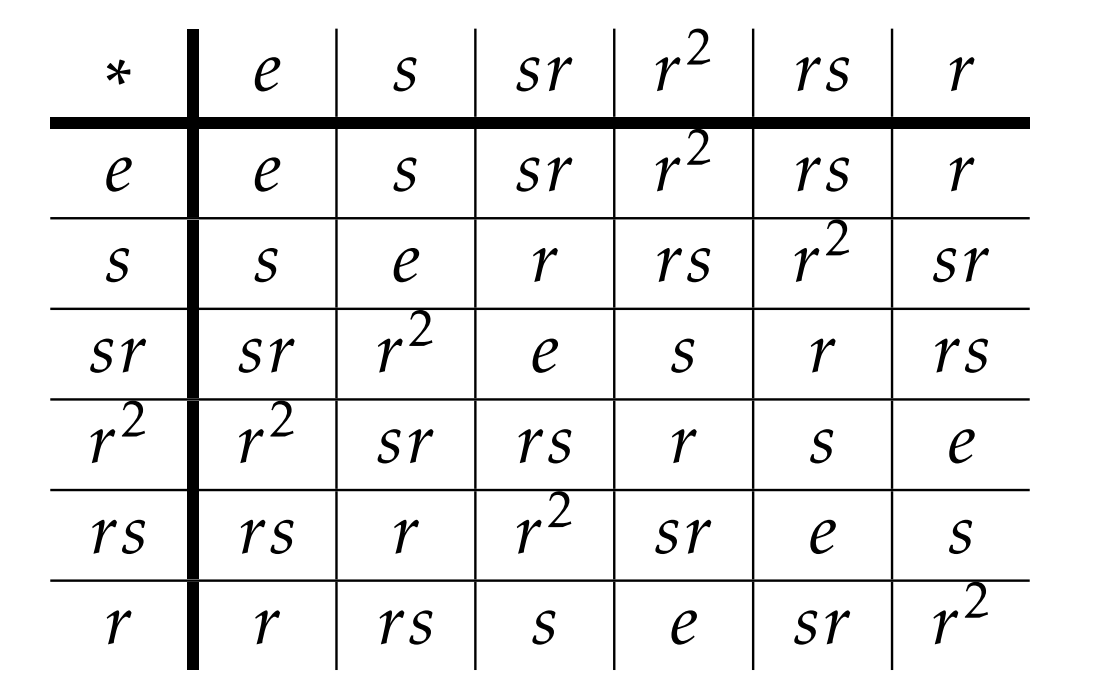
El coset izquierdo\(srH\) debe aparecer en la fila etiquetada por\(sr\) y en las columnas etiquetadas por los elementos de\(H=\{e,s\}\). Lo hemos representado a continuación.
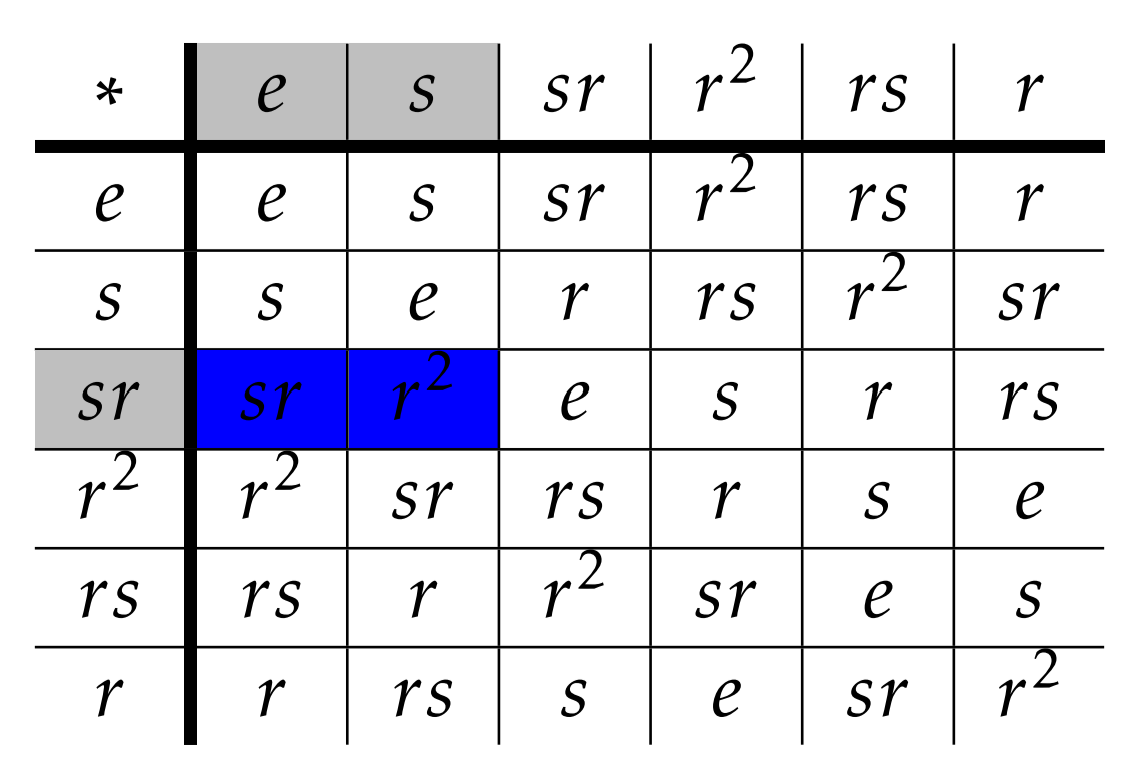
Por otro lado, el coset derecho\(Hsr\) debe aparecer en la columna etiquetada por\(sr\) y las filas etiquetadas por los elementos de\(H=\{e,s\}\):
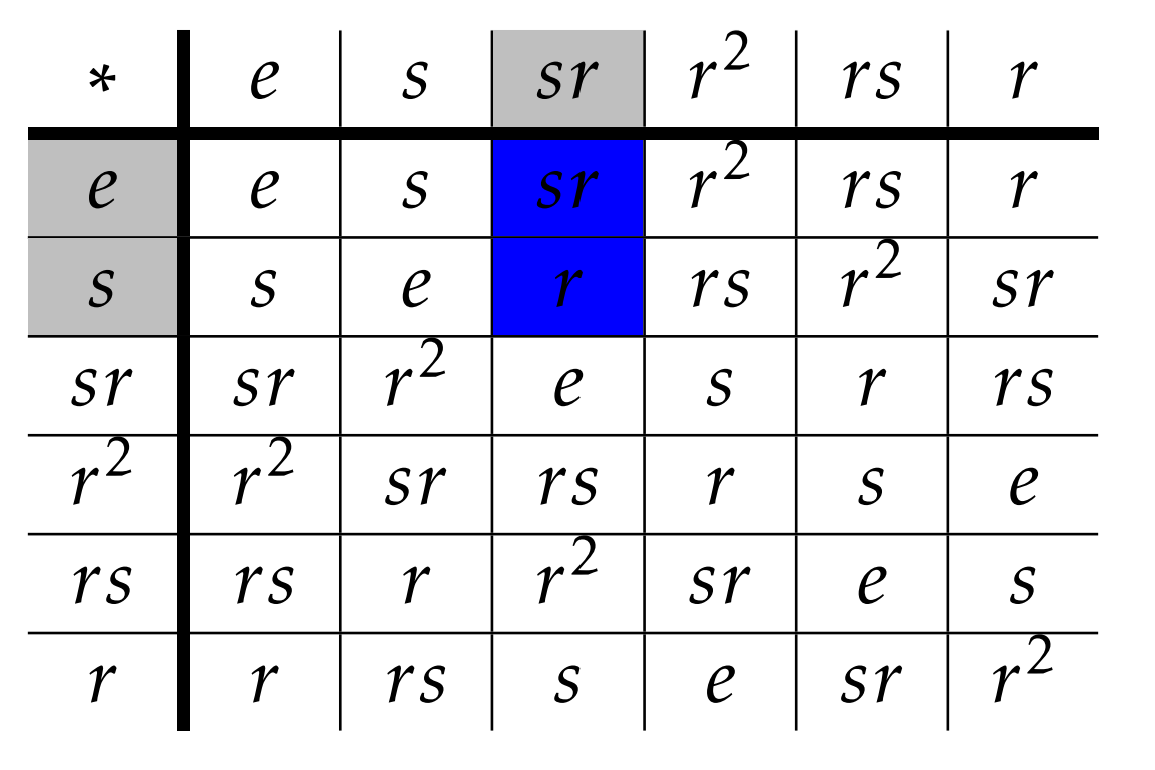
Como podemos ver en las mesas,\(srH\neq Hsr\) ya que\(\{sr,r^2\}\neq \{sr,r\}\). Si coloreamos toda la tabla de grupo para\(D_3\) según cual coset izquierdo pertenece un elemento, obtenemos lo siguiente.
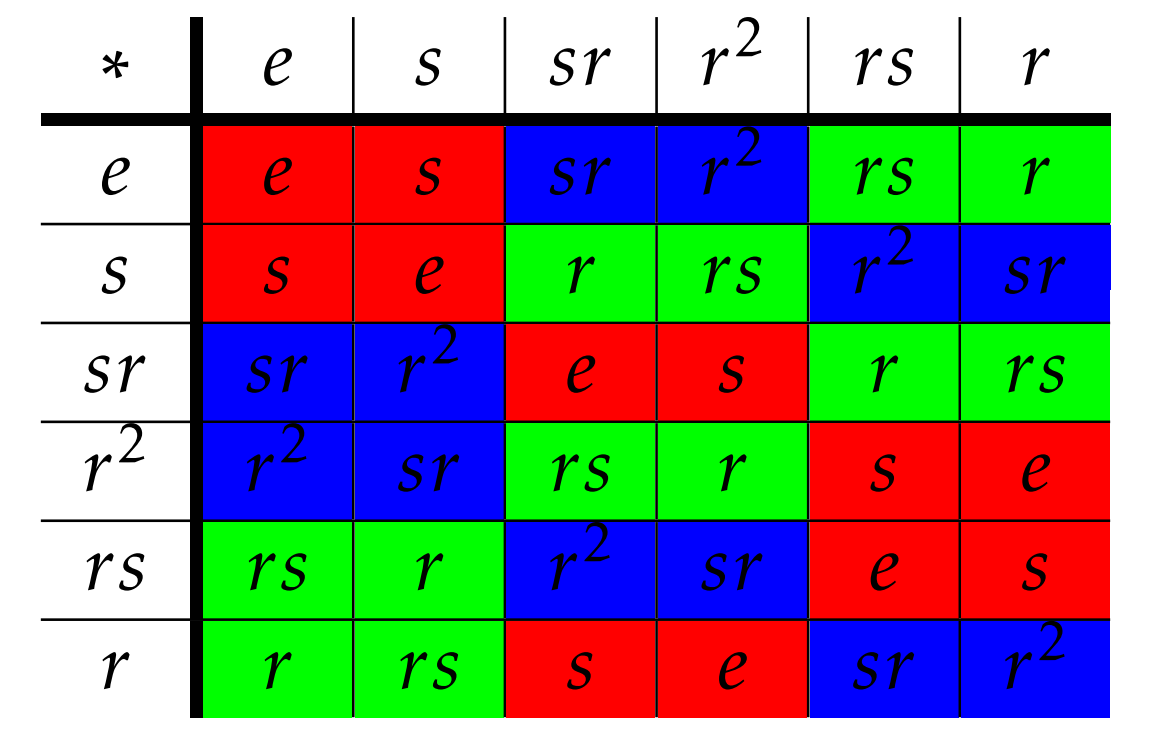
Obtendríamos una tabla similar (pero en este caso, no idéntica) si coloreamos los elementos de acuerdo con los cosets correctos.
Abordemos algunos ejemplos más.
Considerar\(D_3\) y dejar\(K=\langle r\rangle\).
- Encuentra todos los cosets izquierdos de\(K\) y luego encuentra todos los cosets correctos de\(K\) in\(D_3\). ¿Alguna observación?
- Anota la tabla de grupo para\(D_3\), pero esta vez arregla las filas y columnas de acuerdo con los cosets de la izquierda para\(K\). Colorea toda la tabla según la cual izquierda coset pertenece un elemento. ¿Se pueden visualizar las observaciones que realizó en la parte (a)?
Considerar\(Q_8\). Dejar\(H=\langle i\rangle\) y\(K=\langle -1\rangle\).
- Encuentra todos los cosets izquierdos\(H\) y todos los cosets correctos de\(H\) in\(Q_8\).
- Anote la tabla de grupo para de\(Q_8\) manera que las filas y columnas estén dispuestas de acuerdo con los cosets de la izquierda para\(H\). Colorea toda la tabla según la cual izquierda coset pertenece un elemento.
- Encuentra todos los cosets izquierdos\(K\) y todos los cosets correctos de\(K\) in\(Q_8\).
- Anote la tabla de grupo para de\(Q_8\) manera que las filas y columnas estén dispuestas de acuerdo con los cosets de la izquierda para\(K\). Colorea toda la tabla según la cual izquierda coset pertenece un elemento.
Considerar\(S_4\). Encuentra todos los cosets izquierdos y todos los cosets correctos de\(A_4\) in\(S_4\). En lugar de hacer fuerza bruta, trata de ser inteligente. Pista: ¿Qué sucede cuando compones dos permutaciones pares versus una permutación par y una permutación extraña?
Considerar\(\mathbb{Z}_8\). Encuentra todos los cosets izquierdos y todos los cosets correctos de\(\langle 4\rangle\) in\(\mathbb{Z}_8\). ¿Por qué sabes que los cosets izquierdo y derecho son los mismos sin verificar realmente?
Considerar\((\mathbb{Z},+)\). Encuentra todos los cosets izquierdos y todos los cosets correctos de\(3\mathbb{Z}\) in\(\mathbb{Z}\). ¿Por qué sabes que los cosets izquierdo y derecho son los mismos sin verificar realmente?
Seamos\(G\) un grupo y vamos\(H\leq G\). Si\(G\) es abeliano, entonces para todos\(a\in G\),\(aH=Ha\). Es decir, si\(G\) es abeliano, entonces los cosets izquierdos de\(H\) son los mismos que los cosets derechos de\(H\).
\(\PageIndex{1}\)\(\PageIndex{2}\)Ejerce e ilustra que si un grupo no es abeliano, entonces los coconjuntos de un subgrupo pueden o no coincidir. Es decir, saber que el grupo no es abeliano no es suficiente para determinar si los cosets izquierdo y derecho son diferentes.
En todos los ejemplos que hemos visto hasta ahora, los cosets izquierdo y derecho\(G\) particionaron en trozos de igual tamaño. Tenemos que demostrar que esto es cierto en general. Para probar que los cosets forman una partición, definiremos una relación de equivalencia apropiada.
Seamos\(G\) un grupo y vamos\(H\leq G\). Definir\(\sim_L\) y\(\sim_R\) vía
\(a\sim_L b\)si y solo si\(a^{-1}b\in H\)
y
\(a\sim_R b\)si y sólo si\(ab^{-1}\in H\).
Entonces ambos\(\sim_L\) y\(\sim_R\) son relaciones de equivalencia. *
- *
-
Sólo hay que demostrar que cualquiera\(\sim_L\) o\(\sim_R\) es una relación de equivalencia ya que la prueba para el otro es similar.
Dado que\(\sim_L\) y\(\sim_R\) son relaciones de equivalencia, las clases de equivalencia correspondientes forman una partición de\(G\). Si\(a\in G\), entonces las clases de equivalencia “izquierda” y “derecha” que contienen\(a\) están dadas por\[[a]_{\sim_L}=\{g\in G\mid a\sim_L g\}\] y\[[a]_{\sim_R}=\{g\in G\mid a\sim_R g\}.\] El siguiente teorema nos dice que las clases de equivalencia determinadas por\(\sim_L\) y\(\sim_R\) son de hecho la izquierda y la derecha coconjuntos de\(H\leq G\), respectivamente.
Si\(G\) es un grupo y\(H\leq G\), entonces\([a]_{\sim_L}=aH\) y\([a]_{\sim_R}=Ha\) para todos\(a\in G\).
Si\(G\) es un grupo y\(H\leq G\), entonces los coconjuntos de izquierda (respectivamente, derecha)\(H\) forman una partición de\(G\).
A continuación, argumentamos que todos los cosets tienen el mismo tamaño.
Seamos\(G\) un grupo,\(H\leq G\), y\(a\in G\). Definir\(\phi:H\to aH\) vía\(\phi(h)=ah\). Entonces\(\phi\) es uno a uno y sobre.
Seamos\(G\) un grupo y vamos\(H\leq G\). Entonces todos los cosets izquierdo y derecho de\(H\) son del mismo tamaño que\(H\). En otras palabras\(\#(aH)=|H|=\#(Ha)\) para todos\(a\in G\). *
- *
-
Como probablemente se espera,\(\#(aH)\) denota el tamaño de\(aH\). Tenga en cuenta que todo sale bien aunque\(H\) tenga un orden infinito.
El siguiente teorema proporciona una caracterización útil de los coconjuntos. Cada parte puede probarse directamente o apelando a resultados anteriores en esta sección.
Seamos\(G\) un grupo y vamos\(H\leq G\).
- Si\(a\in G\), entonces\(a\in aH\) (respectivamente,\(Ha\)).
- Tenemos\(b\in aH\) (respectivamente,\(Ha\)) si y solo si\(aH=bH\) (respectivamente,\(Ha=Hb\)).
- Si\(a\in H\), entonces\(aH=H=Ha\).
- Si\(a\notin H\), entonces para todos\(h\in H\),\(ah\notin H\) (respectivamente,\(ha \notin H\)).
El resultado de la parte (b) del Teorema\(\PageIndex{4}\) es que los cosets pueden tener diferentes nombres. En particular, si\(b\) es un elemento del coset izquierdo\(aH\), entonces podríamos haber llamado fácilmente al coset por el nombre\(bH\). En este caso, ambos\(a\) y\(b\) se denominan representantes de coset.
El resultado final de esta sección verifica que los clones de un subgrupo en un diagrama de Cayley coinciden con los coconjuntos correctos del subgrupo.
Dejar\(G\) ser un grupo finito con conjunto generador\(S\) y dejar\(H\) ser un subgrupo apropiado de\(G\) y supongamos que podemos visualizar el subgrupo para\(H\) en el diagrama de Cayley para\(G\) usar \(S\)como el grupo electrógenos.
- Si\(g\in G\), verificar que el coset correcto\(Hg\) sea un clon de\(H\). Pista: Supongamos\(s\in S\) y\(h_1, h_2\in H\) tal que hay una flecha etiquetada por\(s\) que apunta de\(h_1\) a\(h_2\). Argumentan que hay una flecha etiquetada\(s\) señalando de\(h_1g\) a\(h_2g\).
- Si\(C\) es un clon de\(H\), demostrar que\(C\) es un coconjunto correcto de\(H\).


