5.2: Teorema de Lagrange
- Page ID
- 117775
Finalmente estamos listos para exponer el Teorema de Lagrange, que lleva el nombre del matemático nacido en Italia Joseph Louis Lagrange. Resulta que Lagrange en realidad no probó el teorema que lleva su nombre. El teorema fue realmente probado por Carl Friedrich Gauss en 1801.
Dejar\(G\) ser un grupo finito y dejar\(H\leq G\). Entonces\(|H|\) divide\(|G|\).
Este teorema de sonido simple es extremadamente poderoso. Una consecuencia es que los grupos y subgrupos tienen una estructura bastante rígida. Supongamos que\(G\) es un grupo finito y vamos\(H\leq G\). Dado que\(G\) es finito, debe haber un número finito de cosets izquierdos distintos, digamos\(H, a_2H, \ldots, a_{n}H\). El corolario 5.1.2 nos dice que cada uno de estos cosets es del mismo tamaño. En particular, el Teorema de Lagrange implica que para cada uno\(i\in\{1,\ldots, n\}\)\(|a_iH|=|G|/n\),, o equivalentemente\(n=|G|/|a_iH|\). Esto se representa en la Figura\(\PageIndex{1}\), donde cada rectángulo representa un coset y hemos etiquetado un solo coset representativo en cada caso.
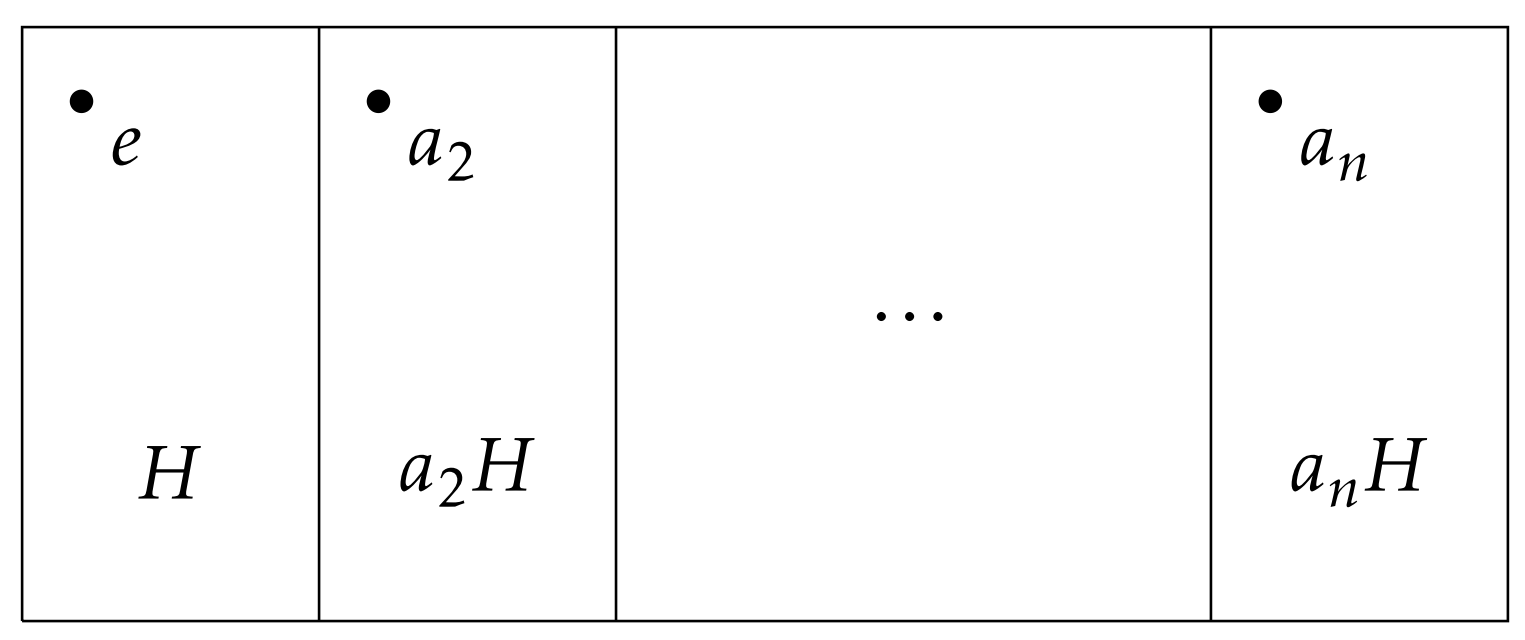
Una consecuencia importante del Teorema de Lagrange es que reduce los tamaños posibles para los subgrupos.
Supongamos que\(G\) es un grupo de orden 48. ¿Cuáles son los pedidos posibles para subgrupos de\(G\)?
El Teorema de Lagrange nos dice cuáles son los órdenes posibles de un subgrupo, pero si\(k\) es un divisor del orden de un grupo, no garantiza que haya un subgrupo de orden\(k\). No es demasiado difícil demostrar que lo contrario del Teorema de Lagrange es cierto para los grupos cíclicos. Sin embargo, no es cierto, en general.
Proporcione un ejemplo de un grupo finito\(G\) tal que\(|G|\) tenga un divisor\(k\) pero\(G\) no tenga un subgrupo de orden\(k\).
Usando el Teorema de Lagrange, podemos probar rápidamente los dos teoremas siguientes.
Dejar\(G\) ser un grupo finito y dejar\(a\in G\). Entonces\(|a|\) divide\(|G|\).
El siguiente ejercicio nos muestra que lo contrario del Teorema no\(\PageIndex{2}\) es cierto.
Argumentan que\(S_4\) no tiene ningún elemento de orden 8.
Por cada prime\(p\), si\(G\) tiene orden\(p\), entonces\(G\cong \mathbb{Z}_p\).
Por cada prime\(p\), hay un grupo único de orden\(p\) hasta el isomorfismo.
El teorema de Lagrange motiva la siguiente definición.
Seamos\(G\) un grupo y vamos\(H\leq G\). El índice de\(H\) in\(G\) es el número de cosets (izquierda o derecha) de\(H\) in\(G\). Equivalentemente, si\(G\) es finito, entonces el índice de\(H\) in\(G\) es igual a\(|G|/|H|\). Denotamos el índice vía\([G:H]\).
Vamos\(H=\langle (1,2)(3,4),(1,3)(2,4)\rangle\).
- Encuentra\([A_4:H]\).
- Encuentra\([S_4:H]\).
Encuentra\([\mathbb{Z}:4\mathbb{Z}]\).


