1.3: Forma paramétrica
- Page ID
- 113125
- Aprender a expresar el conjunto de soluciones de un sistema de ecuaciones lineales en forma paramétrica.
- Comprender las tres posibilidades para el número de soluciones de un sistema de ecuaciones lineales.
- Receta: forma paramétrica.
- Vocabulario palabra: variable libre.
Variables Libres
Existe una posibilidad para la forma de fila reducida de una matriz que no vimos en la Sección 1.2.
Considere el sistema lineal
\[\left\{\begin{array}{rrrrrrc} 2x &+& y &+& 12z &=& 1\\ x &+& 2y &+& 9z &=& -1.\end{array}\right. \nonumber\]
Lo resolvemos usando reducción de filas:
\[\begin{aligned} \left(\begin{array}{ccc|c} 2&1&12&1 \\ 1&2&9&-1 \end{array}\right) \quad\xrightarrow{R_1 \longleftrightarrow R_2}\quad & \left(\begin{array}{ccc|c} \color{red}{1}&2&9&-1 \\ 2&1&12&1 \end{array}\right) &&\color{blue}{\text{(Optional)}} \\ {}\quad\xrightarrow{R_2=R_2-2R_1}\quad & \left(\begin{array}{ccc|c} 1&2&9&-1 \\ \color{red}{0} &-3&-6&3 \end{array}\right) &&\color{blue}{\text{(Step 1c)}} \\ {} \quad\xrightarrow{R_2=R_2\div -3}\quad & \left(\begin{array}{ccc|c} 1&2&9&-1 \\ 0&\color{red}{1} &2&-1 \end{array}\right) &&\color{blue}{\text{(Step 2b)}} \\ {} \quad\xrightarrow{R_1=R_1-2R_2}\quad & \left(\begin{array}{ccc|c} 1&\color{red}{0} &5&1 \\ 0&1&2&-1 \end{array}\right) &&\color{blue}{\text{(Step 2c)}}\end{aligned}\]
Esta matriz de fila reducida corresponde al sistema lineal
\[\left\{\begin{array}{rrrrc} x &+& 5z &=& 1\\ y &+& 2z &=& -1.\end{array}\right. \nonumber\]
¿En qué sentido está resuelto el sistema? Reescribimos como
\[\left\{\begin{array}{rrrrc} x &=& 1& -& 5z \\ y &=& -1& -& 2z\end{array}\right. \nonumber\]
Para cualquier valor de\(z\text{,}\) hay exactamente un valor de\(x\) y\(y\) que hacen que las ecuaciones sean verdaderas. Pero somos libres de elegir cualquier valor de\(z\).
Hemos encontrado todas las soluciones: es el conjunto de todos los valores\(x,y,z\text{,}\) donde
\[\left\{\begin{array}{rrrrr} x &=& 1 &-& 5z\\ y &= &-1& -& 2z\\ z& =& {}&{}& z\end{array}\right. \qquad z\text{ any real number.}\nonumber\]
A esto se le llama la forma paramétrica para la solución al sistema lineal. La variable\(z\) se denomina variable libre.
Dada la forma paramétrica para la solución a un sistema lineal, podemos obtener soluciones específicas reemplazando las variables libres por cualquier número real específico. Por ejemplo, la configuración\(z=0\) en el último ejemplo da la solución\((x,y,z)=(1,-1,0)\text{,}\) y la configuración\(z=1\) da la solución\((x,y,z)=(-4,-3,1)\).
Considerar un sistema consistente de ecuaciones en las variables\(x_1,x_2,\ldots,x_n\). Dejar\(A\) ser una forma escalonada de fila de la matriz aumentada para este sistema.
Decimos que\(x_i\) es una variable libre si su columna correspondiente in no\(A\) es una columna pivote, Definición 1.2.5 en la Sección 1.2.
En el Ejemplo anterior,\(\PageIndex{1}\), la variable\(\color{red}z\) estaba libre debido a que la matriz de forma escalón de fila reducida era
\[\left(\begin{array}{ccc|c} 1&0&\color{red}{5}&1 \\ 0&1&\color{red}{2}&-1\end{array}\right). \nonumber\]
En la matriz
\[\left(\begin{array}{cccc|c} 1&\color{red}{\star} &0&\color{blue}{\star} &\star \\ 0&\color{red}{0}&1&\color{blue}{\star}&\star \end{array}\right),\nonumber\]
las variables libres son\(\color{red}x_2\) y\(\color{blue}x_4\). (La columna aumentada no es libre porque no corresponde a una variable.)
La forma paramétrica del conjunto de soluciones de un sistema consistente de ecuaciones lineales se obtiene de la siguiente manera.
- Escribe el sistema como una matriz aumentada.
- Fila reduce a forma de escalón de fila reducida.
- Escribir el sistema correspondiente (resuelto) de ecuaciones lineales.
- Mueva todas las variables libres al lado derecho de las ecuaciones.
Mover las variables libres al lado derecho de las ecuaciones equivale a resolver para las variables no libres (las que vienen columnas pivotantes) en términos de las variables libres. Se puede pensar en las variables libres como variables independientes, y las variables no libres como dependientes.
El conjunto de soluciones del sistema de ecuaciones lineales
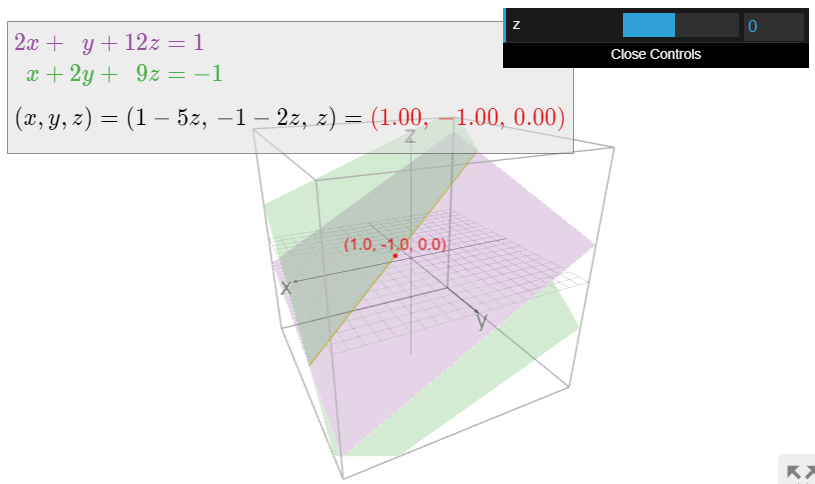
\[\left\{\begin{array}{rrrrrrr} 2x &+& y &+& 12z &=& 1\\ x &+& 2y &+& 9z &=& -1 \end{array}\right. \nonumber\]
es una línea en\(\mathbb{R}^3\text{,}\) como vimos en Ejemplo\(\PageIndex{1}\). Estas ecuaciones se denominan ecuaciones implícitas para la línea: la línea se define implícitamente como las soluciones simultáneas a esas dos ecuaciones.
La forma paramétrica
\[\left\{\begin{array}{rrrrc} x &=& 1 &-& 5z\\ y &=& -1 &-& 2z.\end{array}\right.\nonumber\]
se puede escribir de la siguiente manera:
\[ (x,\,y,\,z) = (1-5z,\,-1-2z,\,z) \qquad \text{$z$ any real number.} \nonumber \]
Esto llamó una ecuación parametrizada para la misma línea. Es una expresión que produce todos los puntos de la línea en términos de un parámetro,\(z\).
Uno debería pensar en un sistema de ecuaciones como una ecuación implícita para su conjunto de soluciones, y en la forma paramétrica como la ecuación parametrizada para el mismo conjunto. La forma paramétrica es mucho más explícita: da una receta concreta para producir todas las soluciones.
Puede elegir cualquier valor para las variables libres en un sistema lineal (consistente).
Las variables libres provienen de las columnas sin pivotes en una matriz en forma de escalón de filas.
Supongamos que la forma de escalón de fila reducida de la matriz para un sistema lineal en cuatro variables\(x_1,x_2,x_3,x_4\) es
\[\left(\begin{array}{cccc|c} 1&\color{red}{0}&0&\color{blue}{3}&2 \\ 0&\color{red}{0}&1&\color{blue}{4}&-1\end{array}\right).\nonumber\]
Las variables libres son\(\color{red}x_2\) y\(\color{blue}x_4\text{:}\) son aquellas cuyas columnas no son columnas pivotantes.
Esto se traduce en el sistema de ecuaciones
\[\left\{\begin{array}{rrrrrrrrr} x_1 &{}&{}&{}&{}&+& 3x_4 &=& 2 \\ {}&{}&{}&{}& x_3 &+& 4x_4 &=& -1\end{array}\right. \quad\xrightarrow{\text{parametric form}}\quad \left\{\begin{array}{rrrrc} x_1 &=& 2 &-& 3x_4\\ x_3 &=& -1 &-& 4x_4. \end{array}\right.\nonumber\]
Lo que le pasó a\(x_2\text{?}\) Es una variable libre, pero ninguna otra variable depende de ello. La solución general al sistema es
\[ (x_1,\,x_2,\,x_3,\,x_4) = (2-3x_4,\,x_2,\,-1-4x_4,\,x_4), \nonumber \]
para cualquier valor de\(x_2\) y\(x_4\). Por ejemplo,\((2,0,-1,0)\) es una solución (con\(x_2=x_4=0\)), y\((5,1,3,-1)\) es una solución (con\(x_2=1, x_4=-1\)).
El sistema de una ecuación lineal
\[ x + y + z = 1 \nonumber \]
proviene de la matriz
\[\left(\begin{array}{ccc|c} 1&1&1&1\end{array}\right),\nonumber\]
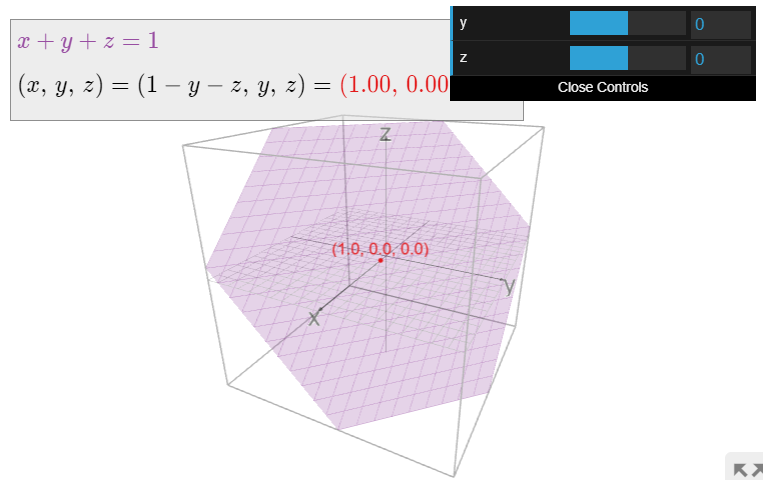
que ya está en forma de escalón de fila reducida. Las variables libres son\(y\) y\(z\). La forma paramétrica para la solución general es
\[ (x,\,y,\,z) = (1 - y - z,\,y,\,z) \nonumber \]
para cualquier valor de\(y\) y\(z\). Esta es la ecuación paramétrica para un plano en\(\mathbb{R}^3\).
Número de soluciones
Hay tres posibilidades para la forma de escalón de fila reducida de la matriz aumentada de un sistema lineal.
- La última columna es una columna pivote. En este caso, el sistema es inconsistente. Hay cero soluciones, es decir, el conjunto de soluciones está vacío. Por ejemplo, la matriz
\[\left(\begin{array}{cc|c} 1&0&\color{red}{0} \\ 0&1&\color{red}{0} \\ 0&0&\color{red}{1}\end{array}\right)\nonumber\]
proviene de un sistema lineal sin soluciones. - Cada columna excepto la última columna es una columna pivotante. En este caso, el sistema cuenta con una solución única. Por ejemplo, la matriz nos
\[\left(\begin{array}{ccc|c} 1&0&0&a \\ 0&1&0&b \\ 0&0&1&c \end{array}\right)\nonumber\]
dice que la solución única es\((x,y,z)=(a,b,c)\). - La última columna no es una columna pivotante, y alguna otra columna tampoco es una columna pivotante. En este caso, el sistema tiene infinitamente muchas soluciones, correspondientes a los infinitamente muchos valores posibles de la (s) variable (s) libre (s). Por ejemplo, en el sistema correspondiente a la matriz
\[\left(\begin{array}{cccc|c} 1&\color{red}{-2}&0&\color{blue}{3}&1\\ 0&\color{red}{0}&1&\color{blue}{4}&-1\end{array}\right),\nonumber\]
cualquier valor para\(\color{red}x_2\) y\(\color{blue}x_4\) dar una solución al sistema de ecuaciones.


