2.2: Ecuaciones vectoriales y vanos

\(\usepackage{macros} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Objetivos

1. Comprender la equivalencia entre un sistema de ecuaciones lineales y una ecuación vectorial.
2. Aprende la definición\(\text{Span}\{x_1,x_2,\ldots,x_k\}\text{,}\) y cómo dibujar imágenes de vanos.
3. Receta: resolver una ecuación vectorial usando matrices aumentadas/decidir si un vector está en un lapso.
4. Imágenes: un sistema inconsistente de ecuaciones, un sistema consistente de ecuaciones, abarca en\(\mathbb{R}^2\) y\(\mathbb{R}^3\).
5. Palabra de vocabulario: ecuación vectorial.
6. Vocabulario esencial palabra: span.

Ecuaciones vectoriales

Una ecuación que involucra vectores con\(n\) coordenadas es lo mismo que\(n\) las ecuaciones que involucran solo números. Por ejemplo, la ecuación

\[x\left(\begin{array}{c}1\\2\\6\end{array}\right) +y\left(\begin{array}{c}-1\\-2\\-1\end{array}\right)=\left(\begin{array}{c}8\\16\\3\end{array}\right)\nonumber\]

simplifica

\[\left(\begin{array}{c}x\\2x\\6x\end{array}\right)+\left(\begin{array}{c}-y\\-2y\\-y\end{array}\right)=\left(\begin{array}{c}8\\16\\3\end{array}\right)\quad\text{or}\quad\left(\begin{array}{c}x-y\\2x-2y\\6x-y\end{array}\right)=\left(\begin{array}{c}8\\16\\3\end{array}\right).\nonumber\]

Para que dos vectores sean iguales, todas sus coordenadas deben ser iguales, así que este es solo el sistema de ecuaciones lineales

\[\left\{\begin{array}{rrrrc}x &-& y &=& 8\\ 2x &-& 2y &=& 16\\ 6x &-& y &=& 3.\end{array}\right.\nonumber\]

Definición\(\PageIndex{1}\): Vector Equation

Una ecuación vectorial es una ecuación que implica una combinación lineal de vectores con coeficientes posiblemente desconocidos.

Nota\(\PageIndex{1}\)

Preguntar si una ecuación vectorial tiene o no una solución es lo mismo que preguntar si un vector dado es una combinación lineal de algunos otros vectores dados.

Por ejemplo, la ecuación vectorial anterior pregunta si el vector\((8,16,3)\) es una combinación lineal de los vectores\((1,2,6)\) y\((-1,2,-1)\).

Lo que realmente nos importa es resolver sistemas de ecuaciones lineales, no resolver ecuaciones vectoriales. El objetivo de las ecuaciones vectoriales es que nos dan una forma diferente, y más geométrica, de visualizar sistemas de ecuaciones lineales.

Nota\(\PageIndex{2}\): A Picture of a Consistent System

A continuación mostraremos que el sistema de ecuaciones anterior es consistente. Equivalentemente, esto significa que la ecuación vectorial anterior tiene una solución. En otras palabras, hay una combinación lineal de\((1,2,6)\) y\((-1,2,-1)\) que es igual\((8,16,3)\). Podemos visualizar la última declaración geométricamente. Por lo tanto, la siguiente Figura\(\PageIndex{1}\) da una imagen de un sistema consistente de ecuaciones. Comparar con Figura\(\PageIndex{2}\), que muestra una imagen de un sistema inconsistente.

Figura\(\PageIndex{1}\): Una imagen de la ecuación vectorial anterior. Intenta resolver la ecuación geométricamente moviendo los deslizadores.

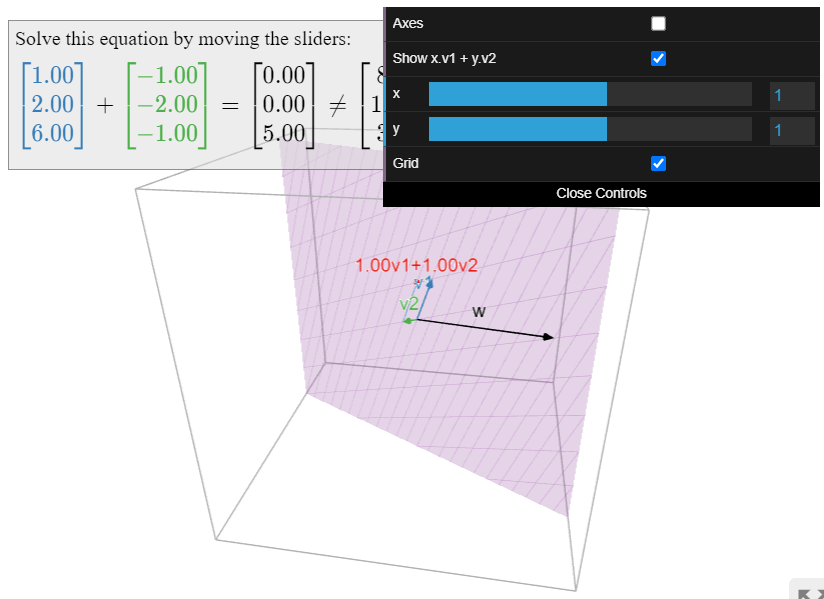
Con el fin de resolver realmente la ecuación vectorial

\[x\color{Red}{\left(\begin{array}{c}1\\2\\6\end{array}\right)} \color{black}{+y}\color{Green}{\left(\begin{array}{c}-1\\-2\\-1\end{array}\right)}\color{black}{=}\color{blue}{\left(\begin{array}{c}8\\16\\3\end{array}\right)}\color{black}{,}\nonumber\]

se tiene que resolver el sistema de ecuaciones lineales

\[\left\{\begin{array}{rrrrc} x &-& y &=& 8\\ 2x &-& 2y &=& 16\\ 6x &-& y &=& 3.\end{array}\right. \nonumber\]

Esto significa formar la matriz aumentada

\[\left(\begin{array}{cc|c}\color{Red}{1}&\color{Green}{-1}&\color{blue}{8} \\ \color{Red}{2}&\color{Green}{-2}&\color{blue}{16}\\ \color{Red}{6}&\color{Green}{-1} &\color{blue}{3}\end{array}\right)\nonumber\]

y reducción de filas. Obsérvese que las columnas de la matriz aumentada son los vectores de la ecuación vectorial original, por lo que en realidad no es necesario escribir el sistema de ecuaciones: se puede ir directamente de la ecuación vectorial a la matriz aumentada “suavizando los vectores juntos”. En Ejemplo\(\PageIndex{1}\) llevamos a cabo la reducción de fila y encontramos la solución.

Ejemplo\(\PageIndex{1}\)

¿Es\(\left(\begin{array}{c}8\\16\\3\end{array}\right)\) una combinación lineal de\(\left(\begin{array}{c}1\\2\\6\end{array}\right)\) y\(\left(\begin{array}{c}-1\\-2\\-1\end{array}\right)\)?

Solución

Como se discutió anteriormente, esta pregunta se reduce a una reducción de fila:

\[\left(\begin{array}{cc|c} 1&-1&8 \\ 2&-2&16 \\ 6&-1&3\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&-1 \\ 0&1&-9 \\ 0&0&0\end{array}\right).\nonumber\]

De esto vemos que la ecuación es consistente, y la solución es\(x=-1\) y\(y=-9\). Concluimos que\(\left(\begin{array}{c}8\\16\\3\end{array}\right)\) es efectivamente una combinación lineal de\(\left(\begin{array}{c}1\\2\\6\end{array}\right)\) y\(\left(\begin{array}{c}-1\\-2\\-1\end{array}\right)\), con coeficientes\(-1\) y\(-9\text{:}\)

\[-\left(\begin{array}{c}1\\2\\6\end{array}\right)-9\left(\begin{array}{c}-1\\-2\\-1\end{array}\right)=\left(\begin{array}{c}8\\6\\3\end{array}\right).\nonumber\]

Receta: Resolver una ecuación vectorial

En general, la ecuación vectorial

\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = b \nonumber \]

donde\(v_1,v_2,\ldots,v_k,\,b\) están los vectores\(\mathbb{R}^n\) y\(x_1,x_2,\ldots,x_k\) son escalares desconocidos, tiene el mismo conjunto de soluciones que el sistema lineal con matriz aumentada

\[\left(\begin{array}{cccc|c} | & |&\quad &|&| \\ v_1 &v_2 &\cdots &v_k &b \\ |&|&\quad &|&|\end{array}\right)\nonumber\]

cuyas columnas son las\(v_i\)'s y\(b\) las'.

Ahora tenemos tres formas equivalentes de pensar sobre un sistema lineal:

1. Como sistema de ecuaciones:
   \[\left\{\begin{array}{rrrrrrr} 2x_1 &+& 3x_2 &-& 2x_3 &=& 7\\ x_1 &-& x_2 &-& 3x_3 &=& 5\end{array}\right.\nonumber\]
2. Como matriz aumentada:
   \[\left(\begin{array}{ccc|c} 2&3&-2&7 \\ 1&-1&-3&5\end{array}\right)\nonumber\]
3. Como una ecuación vectorial (\(x_1v_1 + x_2v_2 + \cdots + x_nv_n = b\)):
   \[x_{1}\left(\begin{array}{c}2\\1\end{array}\right)+x_{2}\left(\begin{array}{c}3\\-1\end{array}\right)+x_{3}\left(\begin{array}{c}-2\\-3\end{array}\right)=\left(\begin{array}{c}7\\5\end{array}\right)\nonumber\]

El tercero es de naturaleza geométrica: se presta a dibujar cuadros.

Se extiende

Será importante saber cuáles son todas las combinaciones lineales de un conjunto de vectores\(v_1,v_2,\ldots,v_k\) en\(\mathbb{R}^n\). En otras palabras, nos gustaría entender el conjunto de todos los vectores de\(\mathbb{R}^n\) tal\(b\) manera que la ecuación vectorial (en las incógnitas\(x_1,x_2,\ldots,x_k\))

\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = b \nonumber \]

tiene una solución (es decir, es consistente).

Definición\(\PageIndex{2}\): Span

Dejen\(v_1,v_2,\ldots,v_k\) ser vectores en\(\mathbb{R}^n\). El lapso de\(v_1,v_2,\ldots,v_k\) es la colección de todas las combinaciones lineales de\(v_1,v_2,\ldots,v_k\text{,}\) y se denota\(\text{Span}\{v_1,v_2,\ldots,v_k\}\). En símbolos:

\[ \text{Span}\{v_1,v_2,\ldots,v_k\} = \bigl\{x_1v_1 + x_2v_2 + \cdots + x_kv_k \mid x_1,x_2,\ldots,x_k \text{ in }\mathbb{R}\bigr\} \nonumber \]

También decimos que\(\text{Span}\{v_1,v_2,\ldots,v_k\}\) es el subconjunto abarcado por o generado por los vectores\(v_1,v_2,\ldots,v_k\).

La definición anterior, Definición\(\PageIndex{2}\) es la primera de varias definiciones esenciales que veremos en este libro de texto. Son esenciales ya que forman la esencia del tema del álgebra lineal: aprender álgebra lineal significa (en parte) aprender estas definiciones. Todas las definiciones son importantes, pero es fundamental que aprendas y entiendas las definiciones marcadas como tales.

Nota\(\PageIndex{3}\): Set Builder Notation

La notación

\[ \bigl\{x_1v_1 + x_2v_2 + \cdots + x_kv_k \mid x_1,x_2,\ldots,x_k \text{ in }\mathbb{R}\bigr\} \nonumber \]

se lee como: “el conjunto de todas las cosas de la forma\(x_1v_1 + x_2v_2 + \cdots + x_kv_k\) tal que\(x_1,x_2,\ldots,x_k\) están en”\(\mathbb{R}\). La línea vertical es “tal que”; todo a la izquierda de ella es “el conjunto de todas las cosas de esta forma”, y todo a la derecha es la condición que esas cosas deben satisfacer para estar en el conjunto. Especificar un conjunto de esta manera se llama notación de generador de conjuntos.

Toda notación matemática es solo taquigrafía: cualquier secuencia de símbolos debe traducirse en una oración habitual.

Nota\(\PageIndex{4}\): Three characterizations of consistency

Ahora tenemos tres formas equivalentes de hacer la misma afirmación:

1. Un vector\(b\) está en el lapso de\(v_1,v_2,\ldots,v_k\).
2. La ecuación vectorial
   \[x_1 v_1 +x_2 v_2 +\cdots +x_k v_k =b\nonumber\]
   tiene una solución.
3. El sistema lineal con matriz aumentada
   \[\left(\begin{array}{cccc|c} |&|&\quad &|&| \\ v_1 &v_2 &\cdots &v_k &b \\ |&|&\quad &|&| \end{array}\right)\nonumber\]
   es consistente.

Equivalente significa que, para cualquier lista dada de vectores\(v_1,v_2,\ldots,v_k,\,b\text{,}\) o bien las tres declaraciones son verdaderas, o las tres declaraciones son falsas.

Figura\(\PageIndex{2}\): Esta es una imagen de un sistema lineal inconsistente: el vector\(w\) en el lado derecho de la ecuación no\(x_1v_1 + x_2v_2 = w\) está en el lapso de\(v_1,v_2\). Convénzase de esto tratando de resolver la ecuación\(x_1v_1 + x_2v_2 = w\) moviendo los controles deslizantes, y por reducción de filas. Compárelo con la Figura\(\PageIndex{1}\).

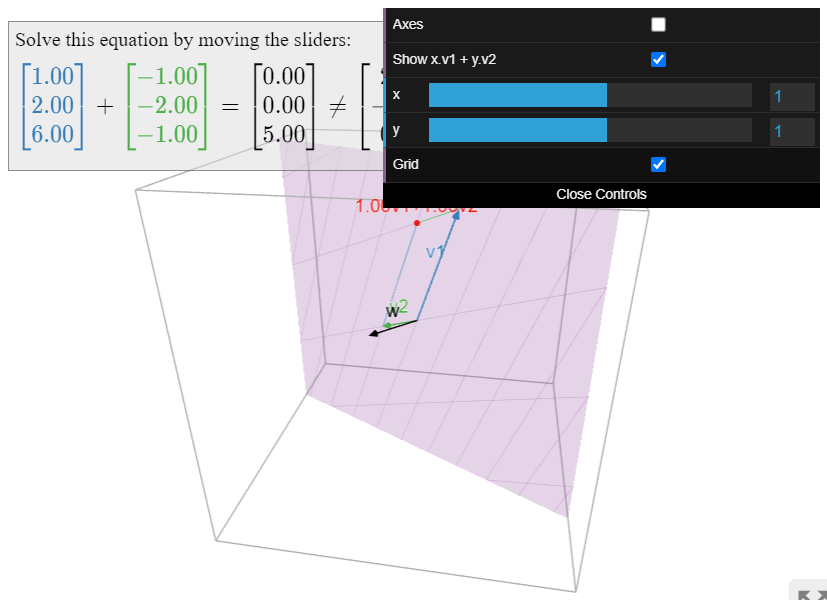
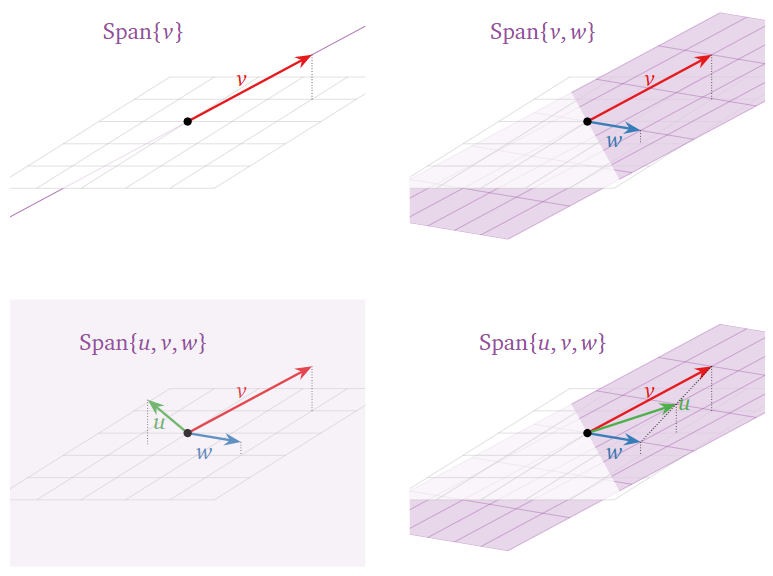
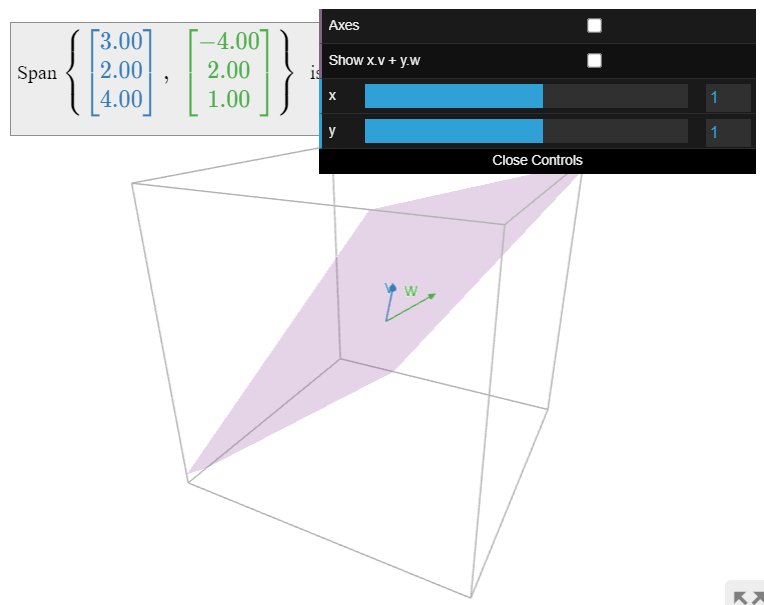
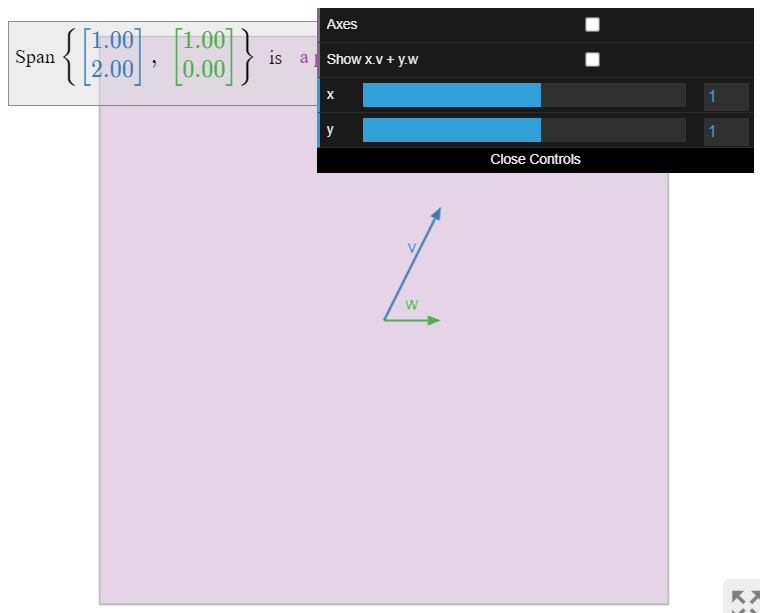
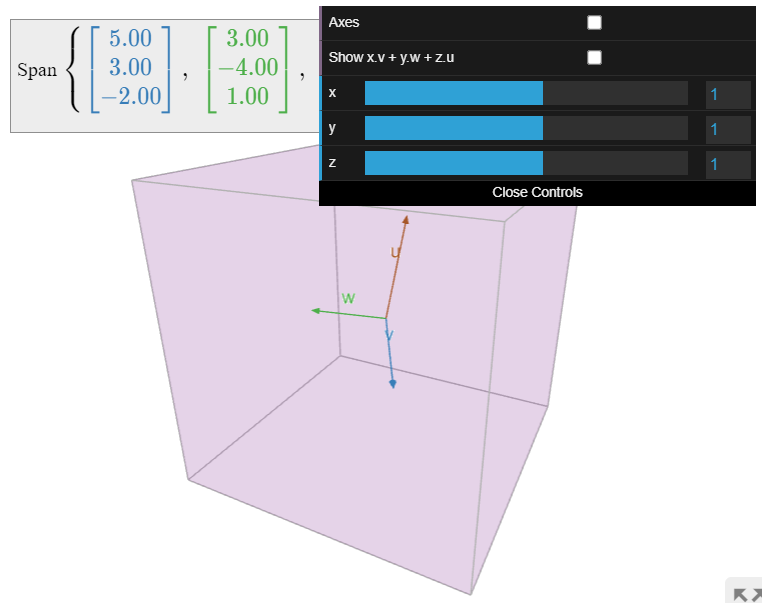
Fotos de Spans.

Dibujar una imagen de\(\text{Span}\{v_1,v_2,\ldots,v_k\}\) es lo mismo que dibujar una imagen de todas las combinaciones lineales de\(v_1,v_2,\ldots,v_k\).

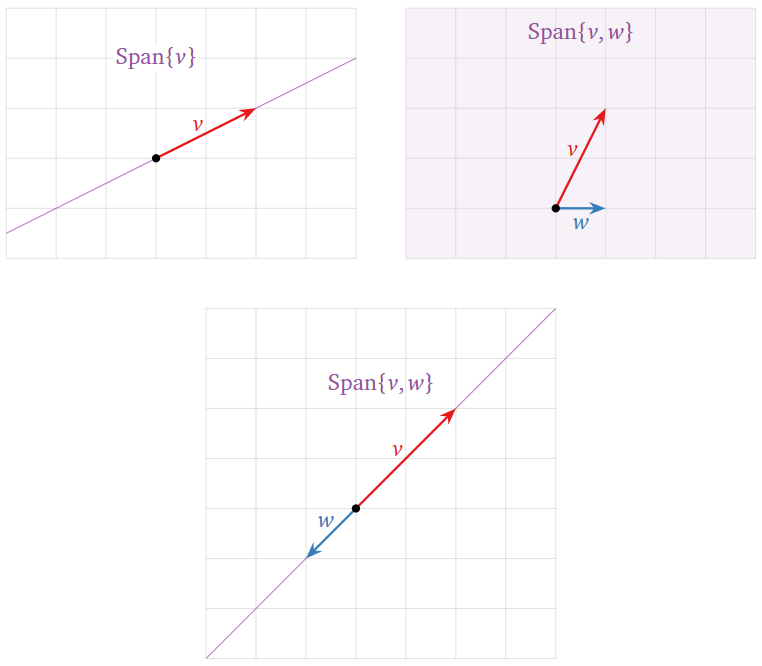
Figura\(\PageIndex{3}\): Imágenes de vanos en\(\mathbb{R}^2\).

Figura\(\PageIndex{4}\): Imágenes de vanos en\(\mathbb{R}^3\). El lapso de dos vectores no colineales es el plano que contiene el origen y las cabezas de los vectores. Tenga en cuenta que tres vectores coplanares (pero no colineales) abarcan un plano y no un espacio de 3, así como dos vectores colineales abarcan una línea y no un plano.

Ejemplo\(\PageIndex{2}\): Interactive: Span of two vectors in \(\mathbb{R}^2\)

Figura\(\PageIndex{5}\): Interactive picture of a span of two vectors in \(\mathbb{R}^2\). Check “Show x.v + y.w” and move the sliders to see how every point in the violet region is in fact a linear combination of the two vectors.

Example \(\PageIndex{3}\): Interactive: Span of two vectors in \(\mathbb{R}^3\)

Figure \(\PageIndex{6}\): Interactive picture of a span of two vectors in \(\mathbb{R}^3\). Check “Show x.v + y.w” and move the sliders to see how every point in the violet region is in fact a linear combination of the two vectors.

Example \(\PageIndex{4}\): Interactive: Span of three vectors in \(\mathbb{R}^3\)

Figura Imagen\(\PageIndex{7}\): interactiva de un lapso de tres vectores en\(\mathbb{R}^3\). Marque “Mostrar x.v + y.w + z.u” y mueva los controles deslizantes para ver cómo cada punto en la región violeta es de hecho una combinación lineal de los tres vectores.