2.3: Ecuaciones Matriciales
- Page ID
- 113042
- Comprender la equivalencia entre un sistema de ecuaciones lineales, una matriz aumentada, una ecuación vectorial y una ecuación matricial.
- Caracterizar los vectores\(b\) tal que\(Ax=b\) sea consistente, en términos del lapso de las columnas de\(A\).
- Caracterizar matrices de\(A\) tal manera que\(Ax=b\) sea consistente para todos los vectores\(b\).
- Receta: multiplicar un vector por una matriz (de dos maneras).
- Imagen: el conjunto de todos los vectores\(b\) tal que\(Ax=b\) es consistente.
- Vocabulario palabra: ecuación matricial.
La ecuación matricial\(Ax=b\)
En esta sección introducimos una forma muy concisa de escribir un sistema de ecuaciones lineales:\(Ax=b\). Aquí\(A\) hay una matriz y\(x,b\) son vectores (generalmente de diferentes tamaños), así que primero debemos explicar cómo multiplicar una matriz por un vector.
Cuando decimos “\(A\)es una\(m\times n\) matriz”, queremos decir que\(A\) tiene\(m\) filas y\(n\) columnas.
En este libro, no reservamos las letras\(m\) y\(n\) para los números de filas y columnas de una matriz. Si escribimos “\(A\)es una\(n\times m\) matriz”, entonces\(n\) es el número de filas de\(A\) y\(m\) es el número de columnas.
Dejar\(A\) ser una\(m\times n\) matriz con columnas\(v_1,v_2,\ldots,v_n\text{:}\)
\[A=\left(\begin{array}{cccc} |&|&\quad &| \\ v_1 &v_2 &\cdots &v_n \\ |&|&\quad &|\end{array}\right)\nonumber\]
El producto de\(A\) con un vector\(x\) en\(\mathbb{R}^n\) es la combinación lineal
\[Ax=\left(\begin{array}{cccc} |&|&\quad &| \\ v_1 &v_2 &\cdots &v_n \\ |&|&\quad &| \end{array}\right)\:\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right) =x_1 v_1 +x_2 v_2 +\cdots +x_n v_n .\nonumber\]
Este es un vector en\(\mathbb{R}^m\).
\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{array}\right)\:\left(\begin{array}{c}1\\2\\3\end{array}\right) =1\left(\begin{array}{c}4\\7\end{array}\right) +2\left(\begin{array}{c}5\\8\end{array}\right)+3\left(\begin{array}{c}6\\9\end{array}\right)=\left(\begin{array}{c}32\\50\end{array}\right).\nonumber\]
\(Ax\)Para que tenga sentido, el número de entradas de\(x\) tiene que ser el mismo que el número de columnas de\(A\text{:}\) estamos utilizando las entradas de\(x\) como los coeficientes de las columnas de\(A\) en una combinación lineal. El vector resultante tiene el mismo número de entradas que el número de filas\(A\text{,}\) ya que cada columna de\(A\) tiene ese número de entradas.
Si\(A\) es una\(m\times n\) matriz (\(m\)filas,\(n\) columnas), entonces tiene\(Ax\) sentido cuando\(x\) tiene\(n\) entradas. El producto\(Ax\) tiene\(m\) entradas.
Dejar\(A\) ser una\(m\times n\) matriz, dejar\(u,v\) ser vectores adentro\(\mathbb{R}^n\text{,}\) y dejar\(c\) ser un escalar. Entonces:
- \(A(u+v) = Au + Av\)
- \(A(cu) = cAu\)
Una ecuación matricial es una ecuación de la forma\(Ax=b\text{,}\) donde\(A\) es una\(m\times n\) matriz,\(b\) es un vector en\(\mathbb{R}^m\text{,}\) y\(x\) es un vector cuyos coeficientes\(x_1,x_2,\ldots,x_n\) son desconocidos.
En este libro estudiaremos dos preguntas complementarias sobre una ecuación matricial\(Ax=b\text{:}\)
- Dada una elección específica de\(b\text{,}\) cuáles son todas las soluciones para\(Ax=b\text{?}\)
- ¿Cuáles son todas las opciones de\(b\) para que\(Ax=b\) sea consistente?
La primera pregunta es más como las preguntas a las que podrías estar acostumbrado de tus cursos anteriores de álgebra; tienes mucha práctica resolviendo ecuaciones como\(x^2-1=0\) para\(x\). La segunda pregunta es quizás un concepto nuevo para ti. El teorema 2.9.1 de la Sección 2.9, que es la culminación de este capítulo, nos dice que las dos preguntas están íntimamente relacionadas.
Dejar\(v_1,v_2,\ldots,v_n\) y\(b\) ser vectores en\(\mathbb{R}^m\). Considerar la ecuación vectorial
\[ x_1v_1 + x_2v_2 + \cdots + x_nv_n = b. \nonumber \]
Esto es equivalente a la ecuación matricial\(Ax=b\text{,}\) donde
\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots &v_n \\ |&|&\quad &|\end{array}\right)\quad\text{and}\quad x=\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right).\nonumber \]
Por el contrario, si\(A\) es cualquier\(m\times n\) matriz, entonces\(Ax=b\) es equivalente a la ecuación vectorial
\[ x_1v_1 + x_2v_2 + \cdots + x_nv_n = b, \nonumber \]
donde\(v_1,v_2,\ldots,v_n\) están las columnas de\(A\text{,}\) y\(x_1,x_2,\ldots,x_n\) son las entradas de\(x\).
Escribir la ecuación vectorial
\[2v_1 +3v_2 -4v_3 =\left(\begin{array}{c}7\\2\\1\end{array}\right)\nonumber\]
como una ecuación matricial, donde\(v_1,v_2,v_3\) están los vectores en\(\mathbb{R}^3\).
Solución
Dejar\(A\) ser la matriz con columnas\(v_1,v_2,v_3\text{,}\) y dejar\(x\) ser el vector con entradas\(2,3,-4\). Entonces
\[Ax=\left(\begin{array}{ccc}|&|&| \\ v_1 & v_2 & v_3 \\ |&|&|\end{array}\right)\:\left(\begin{array}{c}2\\3\\-4\end{array}\right) = 2v_1 +3v_2 -4v_3, \nonumber\]
por lo que la ecuación vectorial es equivalente a la ecuación matricial\(Ax=\left(\begin{array}{c}7\\2\\1\end{array}\right)\).
Ahora tenemos cuatro formas equivalentes de escribir (y pensar) un sistema de ecuaciones lineales:
- Como sistema de ecuaciones:
\[\left\{\begin{array}{rrrrrrr} 2x_1 &+& 3x_2 &-& 2x_3 &=& 7\\ x_1 &-& x_2 &-& 3x_3 &=& 5\end{array}\right.\nonumber\] - Como matriz aumentada:
\[\left(\begin{array}{ccc|c} 2&3&-2&7 \\ 1&-1&-3&5\end{array}\right)\nonumber\] - Como una ecuación vectorial (\(x_1v_1 + x_2v_2 + \cdots + x_nv_n = b\)):
\[x_{1}\left(\begin{array}{c}2\\1\end{array}\right)+x_2\left(\begin{array}{c}3\\-1\end{array}\right)+x_3\left(\begin{array}{c}-2\\-3\end{array}\right)=\left(\begin{array}{c}7\\5\end{array}\right)\nonumber\] - Como una ecuación matricial (\(Ax=b\)):
\[\left(\begin{array}{ccc}2&3&-2 \\ 1&-1&-3\end{array}\right)\:\left(\begin{array}{c}x_1 \\ x_2 \\ x_3\end{array}\right)=\left(\begin{array}{c}7\\5\end{array}\right).\nonumber\]
En particular, los cuatro tienen el mismo conjunto de soluciones.
Vamos a movernos libremente entre las cuatro formas de escribir un sistema lineal, una y otra vez, para el resto del libro.
Otra forma de calcular\(Ax\)
La definición anterior para Producto, Definición\(\PageIndex{1}\), es una forma útil de definir el producto de una matriz con un vector a la hora de entender la relación entre ecuaciones matriciales y ecuaciones vectoriales. Aquí damos una definición que se adapta mejor a los cálculos a mano.
Un vector de fila es una matriz con una fila. El producto de un vector de fila de longitud\(n\) y un vector (columna) de longitud\(n\) es
\[\left(\begin{array}{cccc}a_1 &a_2 &\cdots a_n \end{array}\right)\:\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right) =a_1 x_1 + a_2 x_2 +\cdots + a_n x_n .\nonumber\]
Esto es un escalar.
Si\(A\) es una\(m\times n\) matriz con filas\(r_1,r_2,\ldots,r_m\text{,}\) y\(x\) es un vector en\(\mathbb{R}^n\text{,}\) entonces
\[Ax=\left(\begin{array}{c} — r_1 — \\ —r_2 — \\ \vdots \\ — r_m —\end{array}\right) x=\left(\begin{array}{c} r_1 x \\ r_2 x \\ \vdots \\ r_m x\end{array}\right).\nonumber\]
\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{array}\right)\:\left(\begin{array}{c}1\\2\\3\end{array}\right)=\left(\begin{array}{cc}{\left(\begin{array}{c}4&5&6\end{array}\right)}&{\left(\begin{array}{c}1\\2\\3\end{array}\right)}\\{\left(\begin{array}{ccc}7&8&9\end{array}\right)}&{\left(\begin{array}{c}1\\2\\3\end{array}\right)}\end{array}\right) =\left(\begin{array}{ccccccccccc} 4 & \cdot &1&+&5 &\cdot & 2&+& 6& \cdot & 3 \\ 7 &\cdot & 1&+&8 & \cdot & 2&+&9 & \cdot &3\end{array}\right)=\left(\begin{array}{c} 32\\50\end{array}\right).\nonumber\]
Esta es la misma respuesta que antes:
\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{array}\right)\:\left(\begin{array}{c}1\\2\\3\end{array}\right)=1\left(\begin{array}{c}4\\7\end{array}\right)+2\left(\begin{array}{c}5\\8\end{array}\right)+3\left(\begin{array}{c}6\\9\end{array}\right)=\left(\begin{array}{ccccccccccc} 1 & \cdot & 4&+& 2& \cdot &5&+&3& \cdot &6 \\ 1 & \cdot &7&+& 2& \cdot &8&+&3& \cdot &9\end{array}\right)=\left(\begin{array}{c}32\\50\end{array}\right).\nonumber\]
Vanos y consistencia
Dejar\(A\) ser una matriz con columnas\(v_1,v_2,\ldots,v_n\text{:}\)
\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots & v_n \\ |&|&\quad &|\end{array}\right).\nonumber\]
Entonces
\[ \begin{split} Ax=b&\text{ has a solution} \\ &\iff \text{there exist $x_1,x_2,\ldots,x_n$ such that } A\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right) = b \\ &\iff \text{there exist $x_1,x_2,\ldots,x_n$ such that } x_1v_1 + x_2v_2 + \cdots + x_nv_n = b \\ &\iff \text{$b$ is a linear combination of } v_1,v_2,\ldots,v_n \\ &\iff \text{$b$ is in the span of the columns of $A$}. \end{split} \nonumber \]
La ecuación matricial\(Ax=b\) tiene una solución si y solo si\(b\) está en el lapso de las columnas de\(A\).
Esto da una equivalencia entre una declaración algebraica (\(Ax=b\)es consistente), y una declaración geométrica (\(b\)está en el lapso de las columnas de\(A\)).
Vamos\(A=\left(\begin{array}{cc}2&1\\ -1&0 \\ 1&-1\end{array}\right)\). ¿La ecuación\(Ax=\left(\begin{array}{c}0\\2\\2\end{array}\right)\) tiene una solución?
Solución
Primero respondemos geométricamente a la pregunta. Las columnas de\(A\) son
\[\color{Red}{v_1 =\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right)}\color{black}{,}\nonumber\]
y el vector objetivo (en el lado derecho de la ecuación) es\(\color{Green}{w=\left(\begin{array}{c}0\\2\\2\end{array}\right)}\). La ecuación\(Ax=w\) es consistente si y solo si\(w\) está contenida en el lapso de las columnas de\(A\). Entonces dibujamos un cuadro:
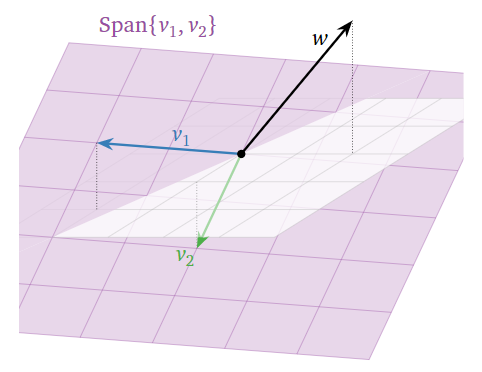
Figura\(\PageIndex{1}\)
No parece que\(w\) se encuentre en\(\text{Span}\{v_1,v_2\},\) lo que la ecuación es inconsistente.
Comprobemos nuestra respuesta geométrica resolviendo la ecuación matricial usando reducción de filas. Ponemos el sistema en una matriz aumentada y la fila reducimos:
\[\left(\begin{array}{cc|c} 2&1&0 \\ -1&0&2 \\ 1&-1&2\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&0 \\ 0&1&0 \\ 0&0&1\end{array}\right).\nonumber\]
La última ecuación es\(0=1\text{,}\) así que el sistema es de hecho inconsistente, y la ecuación matricial
\[\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\right)x=\left(\begin{array}{c}0\\2\\2\end{array}\right)\nonumber\]
no tiene solución.
Vamos\(A=\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\right)\). ¿La ecuación\(Ax=\left(\begin{array}{c}1\\-1\\2\end{array}\right)\) tiene una solución?
Solución
Primero respondemos geométricamente a la pregunta. Las columnas de\(A\) son
\[\color{Red}{v_1=\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right)},\nonumber\]
y el vector objetivo (en el lado derecho de la ecuación) es\(\color{Green}{w=\left(\begin{array}{c}1\\-1\\2\end{array}\right)}\). La ecuación\(Ax=w\) es consistente si y solo si\(w\) está contenida en el lapso de las columnas de\(A\). Entonces dibujamos un cuadro:
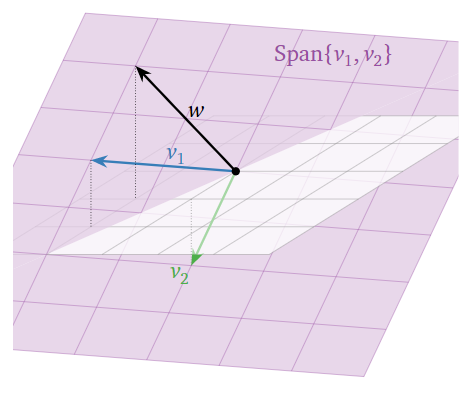
Figura\(\PageIndex{3}\)
Parece que efectivamente\(w\) está contenido en el lapso de las columnas\(A\text{;}\) de hecho, podemos ver
\[ w = v_1 - v_2 \implies x = \left(\begin{array}{c}1\\-1\end{array}\right). \nonumber \]
Comprobemos nuestra respuesta geométrica resolviendo la ecuación matricial usando reducción de filas. Ponemos el sistema en una matriz aumentada y la fila reducimos:
\[\left(\begin{array}{cc|c}2&1&1\\-1&0&-1\\1&-1&2\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&1 \\ 0&1&-1 \\ 0&0&0\end{array}\right).\nonumber\]
Esto nos da\(x=1\) y\(y=-1\text{,}\) que es consistente con el panorama:
\[1\left(\begin{array}{c}2\\-1\\1\end{array}\right)-1\left(\begin{array}{c}1\\0\\-1\end{array}\right)=\left(\begin{array}{c}1\\-1\\2\end{array}\right)\quad\text{or}\quad A\left(\begin{array}{c}1\\-1\end{array}\right)=\left(\begin{array}{c}1\\-1\\2\end{array}\right).\nonumber\]
Cuando las soluciones siempre existen.
Sobre la base de la Nota\(\PageIndex{6}\): Amplios y Consistencia, tenemos el siguiente criterio para cuando\(Ax=b\) es consistente para cada elección de\(b\).
Dejar\(A\) ser una matriz\(m\times n\) (no aumentada). Los siguientes son equivalentes:
- \(Ax=b\)tiene una solución para todos\(b\) en\(\mathbb{R}^m\).
- El lapso de las columnas de\(A\) es todo de\(\mathbb{R}^m\).
- \(A\)tiene una posición de pivote, Definición 1.2.5 en la Sección 1.2, en cada fila.
- Prueba
-
La equivalencia de 1 y 2 se establece por la Nota\(\PageIndex{6}\): Vanos y Consistencia tal como se aplica a cada\(b\) in\(\mathbb{R}^m\).
Ahora demostramos que 1 y 3 son equivalentes. (Como sabemos que 1 y 2 son equivalentes, esto implica que 2 y 3 son equivalentes también). Si\(A\) tiene un pivote en cada fila, entonces su forma de escalón de fila reducida se ve así:
\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&1&\star \end{array}\right),\nonumber\]
y por lo tanto\(\left(\begin{array}{c|c}A&b\end{array}\right)\) reduce a esto:
\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &\star \\ 0&1&\star &0&\star &\star \\ 0&0&0&1&\star &\star\end{array}\right).\nonumber\]
No hay\(b\) que lo haga inconsistente, así que siempre hay una solución. Por el contrario, si\(A\) no tiene un pivote en cada fila, entonces su forma de escalón de fila reducida se ve así:
\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&0&0\end{array}\right),\nonumber\]
que puede dar lugar a un sistema inconsistente después de aumentar con\(b\text{:}\)
\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &0 \\ 0&1&\star &0&\star &0 \\ 0&0&0&0&0&16\end{array}\right).\nonumber\]
Recordemos que equivalente significa que, para cualquier matriz dada\(A\text{,}\) o bien todas las condiciones del Teorema anterior\(\PageIndex{1}\),, son verdaderas, o todas son falsas.
Tenga cuidado al leer el enunciado del Teorema anterior,\(\PageIndex{1}\). The first two conditions look very much like this Note \(\PageIndex{6}\): Spans and Consistency, but they are logically quite different because of the quantifier “ para todos\(b\)”.
Veremos en este Corolario 2.7.1 de la Sección 2.7 que la dimensión del lapso de las columnas es igual al número de pivotes de\(A\). Es decir, las columnas de\(A\) abarcan una línea si\(A\) tiene un pivote, abarcan un plano si\(A\) tiene dos pivotes, etc. todo el espacio\(\mathbb{R}^m\) tiene dimensión\(m\text{,}\) por lo que esto generaliza el hecho de que las columnas de\(A\) span\(\mathbb{R}^m\) cuando\(A\) tiene\(m\) pivotes.