2.4: Conjuntos de soluciones
- Page ID
- 113023
- Comprender la relación entre el conjunto de soluciones de\(Ax=0\) y el conjunto de soluciones de\(Ax=b\).
- Entender la diferencia entre el conjunto de soluciones y el lapso de columna.
- Recetas: forma vectorial paramétrica, escribir el conjunto de soluciones de un sistema homogéneo como un span.
- Imágenes: conjunto de soluciones de un sistema homogéneo, conjunto de soluciones de un sistema no homogéneo, la relación entre los dos.
- Palabras del vocabulario: solución homogénea /no homogénea, trivial.
En esta sección estudiaremos la geometría del conjunto de soluciones de cualquier ecuación matricial\(Ax=b\).
Sistemas Homogéneos
La ecuación\(Ax=b\) es más fácil de resolver cuando\(b=0\text{,}\) así empezamos con este caso.
Un sistema de ecuaciones lineales de la forma\(Ax=0\) se llama homogéneo.
Un sistema de ecuaciones lineales de la forma\(Ax=b\) for\(b\neq 0\) se llama no homogéneo.
Un sistema homogéneo es solo un sistema de ecuaciones lineales donde todas las constantes en el lado derecho del signo igual son cero.
Un sistema homogéneo siempre tiene la solución\(x=0\). A esto se le llama la solución trivial. Cualquier solución distinta de cero se llama no trivial.
La ecuación\(Ax=0\) tiene una solución no trivial\(\iff\) hay una variable libre\(\iff\)\(A\) tiene una columna sin una posición de pivote.
¿Cuál es el conjunto de soluciones de\(Ax=0\text{,}\) dónde
\[A=\left(\begin{array}{ccc}1&3&4\\2&-1&2\\1&0&1\end{array}\right)?\nonumber\]
Solución
Formamos una matriz aumentada y la fila reducimos:
\[\left(\begin{array}{ccc|c}1&3&4&0\\2&-1&2&0\\1&0&1&0\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{ccc|c}1&0&0&0\\0&1&0&0\\0&0&1&0\end{array}\right).\nonumber\]
La única solución es la solución trivial\(x=0\).
Cuando hacemos fila reducir la matriz aumentada para un sistema homogéneo de ecuaciones lineales, la última columna será cero durante todo el proceso de reducción de filas. Esto lo vimos en el último Ejemplo\(\PageIndex{1}\):
\[\left(\begin{array}{ccc|c}1&3&4&0\\2&-1&2&0\\1&0&1&0\end{array}\right)\nonumber\]
Por lo que no es realmente necesario escribir matrices aumentadas a la hora de resolver sistemas homogéneos.
Cuando la ecuación\(Ax=0\) homogénea tiene soluciones no triviales, resulta que el conjunto de soluciones se puede expresar convenientemente como un lapso.
Considere la siguiente matriz en forma de escalón de fila reducida:
\[A=\left(\begin{array}{cccc}1&0&-8&-7 \\ 0&1&4&3 \\ 0&0&0&0\end{array}\right).\nonumber\]
La ecuación matricial\(Ax=0\) corresponde al sistema de ecuaciones
\[\left\{\begin{array}{rrrrrrrrl} x_1&{}&{}& -& 8x_3 &-& 7x_4 &=& 0 \\ {}&{}& x_2 &+& 4x_3 &+& 3x_4 &=& 0.\end{array}\right.\nonumber\]
Podemos escribir la forma paramétrica de la siguiente manera:
\[\left\{\begin{array}{rrrrc} x_1 &=& 8x_3 &+& 7x_4 \\ x_2 &=& -4x_3 &-& 3x_4 \\ x_3 &=& x_3 &{}&{} \\ x_4 &=& {}&{}& x_4.\end{array}\right.\nonumber\]
Escribimos las ecuaciones redundantes\(x_3=x_3\) y\(x_4=x_4\) para convertir el sistema anterior en una ecuación vectorial:
\[x=\left(\begin{array}{c}x_1 \\ x_2 \\ x_3 \\ x_4\end{array}\right)=x_3 \left(\begin{array}{c}8\\-4\\1\\0\end{array}\right)+x_4 \left(\begin{array}{c}7\\-3\\0\\1\end{array}\right).\nonumber\]
Esta ecuación vectorial se llama la forma vectorial paramétrica del conjunto de soluciones. Ya que\(x_3\) y\(x_4\) se les permite ser cualquier cosa, esto dice que el conjunto de soluciones es el conjunto de todas las combinaciones lineales de\(\left(\begin{array}{c}8\\-4\\1\\0\end{array}\right)\) y\(\left(\begin{array}{c}7\\-3\\0\\1\end{array}\right)\). En otras palabras, el conjunto de soluciones es
\[\text{Span}\left\{\left(\begin{array}{c}8\\-4\\1\\0\end{array}\right),\:\left(\begin{array}{c}7\\-3\\0\\1\end{array}\right)\right\}.\nonumber\]
Aquí está el procedimiento general.
\(A\)Déjese ser una\(m\times n\) matriz. Supongamos que las variables libres en la ecuación homogénea\(Ax=0\) son, por ejemplo,\(x_3\text{,}\)\(x_6\text{,}\) y\(x_8\).
- Encuentra la forma de escalón de fila reducida de\(A\).
- Escriba la forma paramétrica del conjunto de soluciones, incluidas las ecuaciones redundantes\(x_3=x_3\text{,}\)\(x_6=x_6\text{,}\)\(x_8=x_8\). Poner ecuaciones para todos los\(x_i\) en orden.
- Haga una ecuación de vector único a partir de estas ecuaciones haciendo los coeficientes de\(x_3,x_6,\) y\(x_8\) en vectores\(v_3,v_6,\) y\(v_8\text{,}\) respectivamente.
Las soluciones a\(Ax=0\) se expresarán entonces en la forma
\[ x = x_3v_3 + x_6v_6 + x_8v_8 \nonumber \]
para algunos vectores\(v_3,v_6,v_8\) en\(\mathbb{R}^n\text{,}\) y cualquier escalar\(x_3,x_6,x_8\). A esto se le llama la forma vectorial paramétrica de la solución.
En este caso, el conjunto de soluciones se puede escribir como\(\text{Span}\{v_3,\,v_6,\,v_8\}.\)
Destacamos en particular el siguiente hecho.
El conjunto de soluciones a una ecuación homogénea\(Ax=0\) es un span.
Compute la forma vectorial paramétrica del conjunto de soluciones de\(Ax=0\text{,}\) donde
\[A=\left(\begin{array}{cc}1&-3\\2&-6\end{array}\right).\nonumber\]
Solución
Remonamos reducir (sin aumentar, como se sugiere en la Observación anterior\(\PageIndex{2}\)):
\[\left(\begin{array}{cc}1&-3\\2&-6\end{array}\right)\quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc}1&-3\\0&0\end{array}\right).\nonumber\]
Esto corresponde a la ecuación única\(x_1 - 3x_2=0\). Escribimos la forma paramétrica incluyendo la ecuación redundante\(x_2=x_2\text{:}\)
\[\left\{\begin{array}{rrc} x_1 &=& 3x_2 \\ x_2 &=& x_2.\end{array}\right.\nonumber\]
Los convertimos en una sola ecuación vectorial:
\[x=\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=x_2\left(\begin{array}{c}3\\1\end{array}\right).\nonumber\]
Esta es la forma vectorial paramétrica del conjunto de soluciones. Ya que\(x_2\) se permite que sea cualquier cosa, esto dice que el conjunto de soluciones es el conjunto de todos los múltiplos escalares de\({3\choose 1}\text{,}\) otros conocidos como
\[\text{Span}\left\{\left(\begin{array}{c}3\\1\end{array}\right)\right\}.\nonumber\]
Sabemos dibujar el cuadro de un lapso de un vector: es una línea. Por lo tanto, esta es una imagen del conjunto de soluciones:
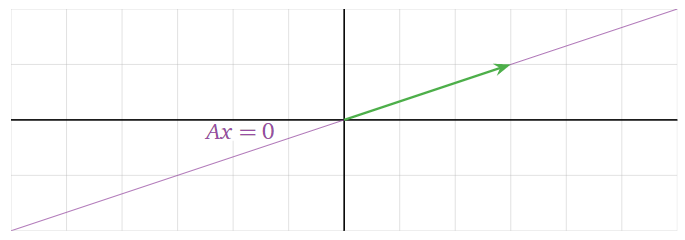
Figura\(\PageIndex{1}\)
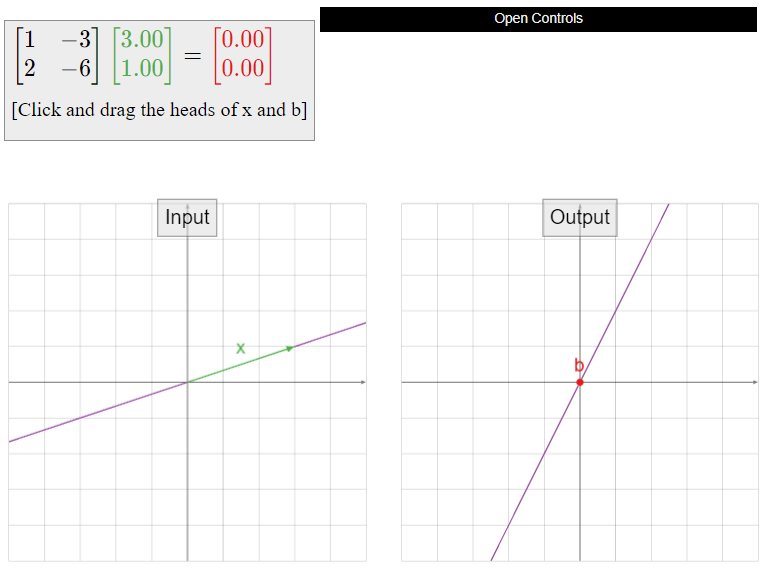
Dado que hubo dos variables en el Ejemplo anterior\(\PageIndex{3}\), el conjunto de soluciones es un subconjunto de\(\mathbb{R}^2\). Como una de las variables era libre, el conjunto de soluciones es una línea:
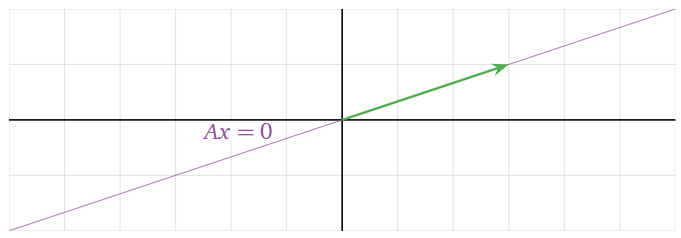
Figura\(\PageIndex{3}\)
Para encontrar realmente una solución no trivial a\(Ax=0\) en el Ejemplo anterior\(\PageIndex{3}\), basta con sustituir cualquier valor distinto de cero por la variable libre\(x_2\). Por ejemplo, tomar\(x_2=1\) da la solución no trivial\(x = 1\cdot{3\choose 1} = {3\choose 1}.\) Comparar con esta nota en la Sección 1.3, Nota 1.3.1.
Compute la forma vectorial paramétrica del conjunto de soluciones de\(Ax=0\text{,}\) donde
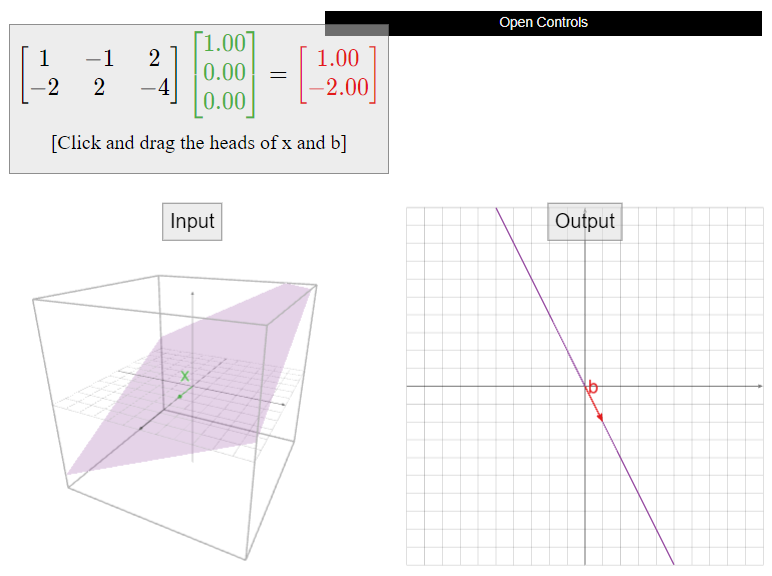
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right).\nonumber\]
Solución
Remonamos reducir (sin aumentar, como se sugiere en la Observación anterior\(\PageIndex{2}\)):
\[\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{ccc}1&-1&2 \\ 0&0&0\end{array}\right).\nonumber\]
Esto corresponde a la ecuación única\(x_1 - x_2 + 2x_3 = 0\). Escribimos la forma paramétrica incluyendo las ecuaciones redundantes\(x_2=x_2\) y\(x_3=x_3\text{:}\)
\[\left\{\begin{array}{rrrrc}x_1 &=& x_2 &-& 2x_3 \\ x_2 &=& x_2 &{}&{} \\ x_3 &=& {}&{}& x_3.\end{array}\right.\nonumber\]
Los convertimos en una sola ecuación vectorial:
\[x=\left(\begin{array}{c}x_1 \\ x_2 \\x_3\end{array}\right) =x_2\left(\begin{array}{c}1\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right).\nonumber\]
Esta es la forma vectorial paramétrica del conjunto de soluciones. Ya que\(x_2\) y\(x_3\) se les permite ser cualquier cosa, esto dice que el conjunto de soluciones es el conjunto de todas las combinaciones lineales de\(\left(\begin{array}{c}1\\1\\0\end{array}\right)\) y\(\left(\begin{array}{c}-2\\0\\1\end{array}\right)\). En otras palabras, el conjunto de soluciones es
\[\text{Span}\left\{\left(\begin{array}{c}1\\1\\0\end{array}\right),\:\left(\begin{array}{c}-2\\0\\1\end{array}\right)\right\}.\nonumber\]
Sabemos dibujar el lapso de dos vectores no colineales en\(\mathbb{R}^3\text{:}\) él es un plano. Por lo tanto, esta es una imagen del conjunto de soluciones:
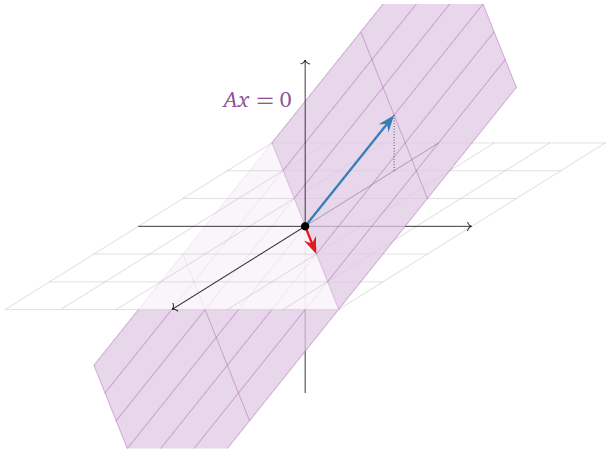
Figura\(\PageIndex{4}\)
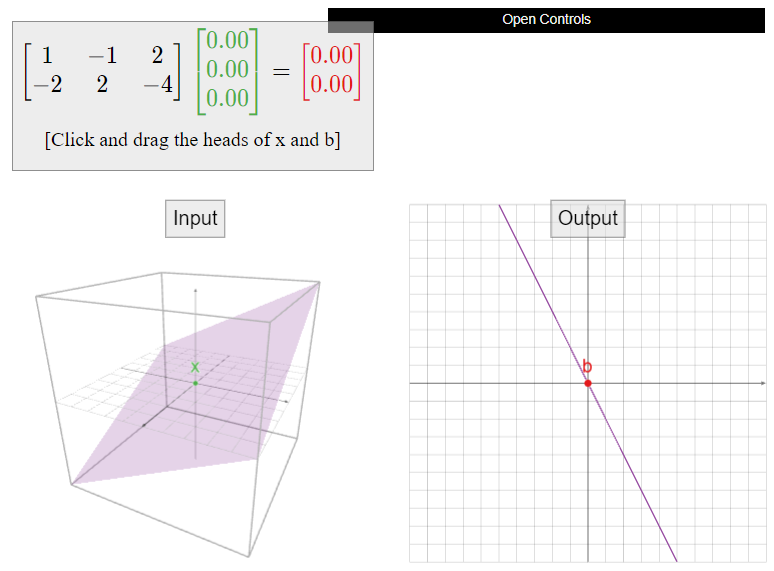
Dado que hubo tres variables en el Ejemplo anterior\(\PageIndex{4}\), el conjunto de soluciones es un subconjunto de\(\mathbb{R}^3\). Dado que dos de las variables eran libres, el conjunto de soluciones es un plano.
Hay una pregunta natural que hacer aquí: ¿es posible escribir la solución a una ecuación matricial homogénea usando menos vectores que el dado en la receta anterior? Veremos en el Ejemplo 2.5.3 de la Sección 2.5 que la respuesta es no: los vectores de la receta son siempre linealmente independientes, lo que significa que no hay forma de escribir la solución con menos vectores.
Otra pregunta natural es: ¿los conjuntos de soluciones para ecuaciones inhomogéneas también abarcan? Como veremos en breve, nunca son vanos, sino que están estrechamente relacionados con vanos.
Existe una relación natural entre el número de variables libres y el “tamaño” del conjunto de soluciones, de la siguiente manera.
Los ejemplos anteriores nos muestran el siguiente patrón: cuando hay una variable libre en una ecuación matricial consistente, el conjunto de soluciones es una línea, y cuando hay dos variables libres, el conjunto de soluciones es un plano, etc. El número de variables libres se llama la dimensión del conjunto de soluciones.
Desarrollaremos una definición rigurosa, Definición 2.7.2, de dimensión en la Sección 2.7, pero por ahora la dimensión simplemente significará el número de variables libres. Compare con esta importante nota en la Sección 2.5, Nota 2.5.5.
Intuitivamente, la dimensión de un conjunto de soluciones es el número de parámetros que necesita para describir un punto en el conjunto de soluciones. Para una línea solo se necesita un parámetro, y para un plano se necesitan dos parámetros. Esto es similar a cómo la ubicación de un edificio en la calle Peachtree, que es como una línea, está determinada por un número y cómo una esquina de una calle en Manhattan, que es como un avión, se especifica con dos números.
Sistemas no homogéneos
Recordemos que una ecuación matricial\(Ax=b\) se llama no homogénea cuando\(b\neq0\).
¿Cuál es el conjunto de soluciones de\(Ax=b\text{,}\) dónde
\[A=\left(\begin{array}{cc}1&-3 \\ 2&-6\end{array}\right)\quad\text{and}\quad b=\left(\begin{array}{c}-3\\-6\end{array}\right)?\nonumber\]
(Compárese con este Ejemplo\(\PageIndex{4}\), donde resolvimos la ecuación homogénea correspondiente.)
Solución
Remaremos reducir la matriz aumentada asociada:
\[\left(\begin{array}{cc|c} 1&-3&-3 \\ 2&-6&-6\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&-3&-3 \\ 0&0&0\end{array}\right).\nonumber\]
Esto corresponde a la ecuación única\(x_1 - 3x_2 = -3\). Podemos escribir la forma paramétrica de la siguiente manera:
\[\left\{\begin{array}{rrrrl} x_1 &=& 3x_2 &-& 3\\ x_2 &=& x_2 &+& 0.\end{array}\right.\nonumber\]
Convertimos el sistema anterior en una ecuación vectorial:
\[x=\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=x_2\left(\begin{array}{c}3\\1\end{array}\right)+\left(\begin{array}{c}-3\\0\end{array}\right).\nonumber\]
Esta ecuación vectorial se llama la forma vectorial paramétrica del conjunto de soluciones. Escribimos el conjunto de soluciones como
\[\text{Span}\left\{\left(\begin{array}{c}3\\1\end{array}\right)\right\}+\left(\begin{array}{c}-3\\0\end{array}\right).\nonumber\]
Aquí hay una imagen del conjunto de soluciones:
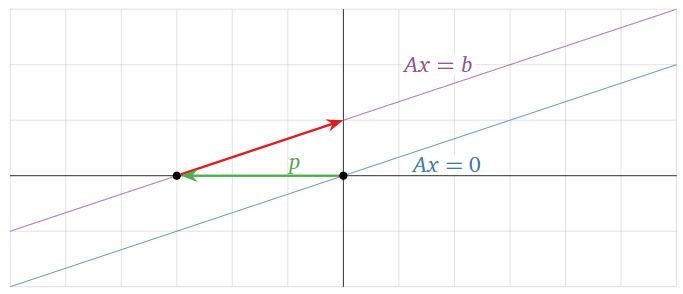
Figura\(\PageIndex{6}\)
En el Ejemplo anterior\(\PageIndex{5}\), el conjunto de soluciones fueron todos los vectores de la forma
\[x=\left(\begin{array}{c}x_1 \\ x_2\end{array}\right)=x_2\left(\begin{array}{c}3\\1\end{array}\right)+\left(\begin{array}{c}-3\\0\end{array}\right)\nonumber\]
donde\(x_2\) está cualquier escalar. El vector\(p = {-3\choose 0}\) es también una solución de\(Ax=b\text{:}\) toma\(x_2=0\). Llamamos a\(p\) una solución particular.
En el conjunto de soluciones,\(x_2\) se permite que sea cualquier cosa, y así el conjunto de soluciones se obtiene de la siguiente manera: tomamos todos los múltiplos escalares de\({3\choose 1}\) y luego agregamos la solución particular\(p = {-3\choose 0}\) a cada uno de estos múltiplos escalares. Geométricamente, esto se logra dibujando primero el lapso de la\({3\choose 1}\text{,}\) cual es una línea a través del origen (y, no casualmente, la solución a\(Ax=0\)), y traducimos, o empujamos, esta línea a lo largo\(p = {-3\choose 0}\). La línea traducida contiene\(p\) y es paralela a\(\text{Span}\{{3\choose 1}\}\text{:}\) ella es una traducción de una línea.
Figura\(\PageIndex{8}\)
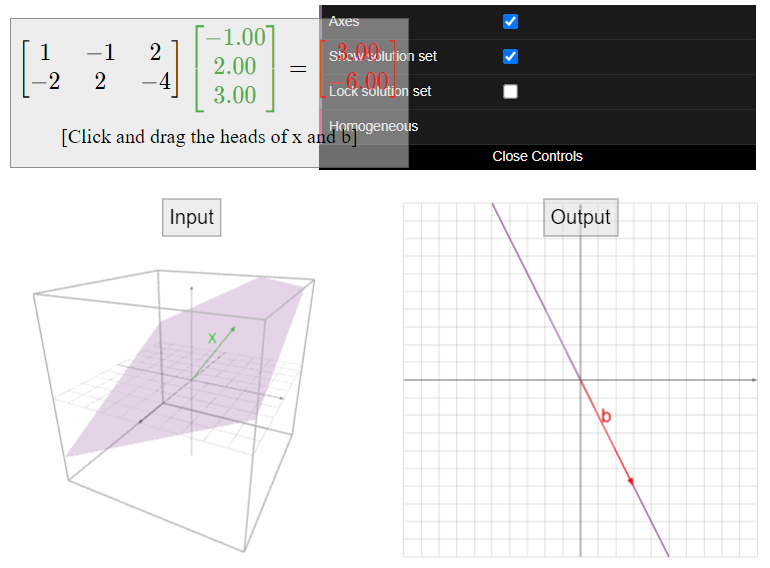
¿Cuál es el conjunto de soluciones de\(Ax=b\text{,}\) dónde
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right)\quad\text{and}\quad b=\left(\begin{array}{c}1\\-2\end{array}\right)?\nonumber\]
(Compare este Ejemplo\(\PageIndex{4}\).)
Solución
Remaremos reducir la matriz aumentada asociada:
\[\left(\begin{array}{ccc|c} 1&-1&2&1 \\ -2&2&-4&-2\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cccc}1&-1&2&1 \\ 0&0&0&0\end{array}\right).\nonumber\]
Esto corresponde a la ecuación única\(x_1 - x_2 + 2x_3 = 1\). Podemos escribir la forma paramétrica de la siguiente manera:
\[\left\{\begin{array}{rrrrrrl} x_1 &=& x_2 &-& 2x_3 &+& 1\\ x_2 &=& x_2 &{}&{}& +& 0\\ x_3 &=&{}&{}& x_3 &+& 0.\end{array}\right.\nonumber\]
Convertimos el sistema anterior en una ecuación vectorial:
\[x=\left(\begin{array}{c}x_1 \\x_2\\x_3\end{array}\right)=x_{2}\left(\begin{array}{c}1\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right)+\left(\begin{array}{c}1\\0\\0\end{array}\right).\nonumber\]
Esta ecuación vectorial se llama la forma vectorial paramétrica del conjunto de soluciones. Ya que\(x_2\) y\(x_3\) se les permite ser cualquier cosa, esto dice que el conjunto de soluciones es el conjunto de todas las combinaciones lineales de\(\left(\begin{array}{c}1\\1\\1\end{array}\right)\) y\(\left(\begin{array}{c}-2\\0\\1\end{array}\right)\), traducido por el vector\(p=\left(\begin{array}{c}1\\0\\0\end{array}\right)\). Este es un plano que contiene\(p\) y es paralelo a\(\text{Span}\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\left(\begin{array}{c}-2\\0\\1\end{array}\right)\right\}\text{:}\) él es un traducir de un plano. Escribimos el conjunto de soluciones como
\[\text{Span}\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\left(\begin{array}{c}-2\\0\\1\end{array}\right)\right\} +\left(\begin{array}{c}1\\0\\0\end{array}\right).\nonumber\]
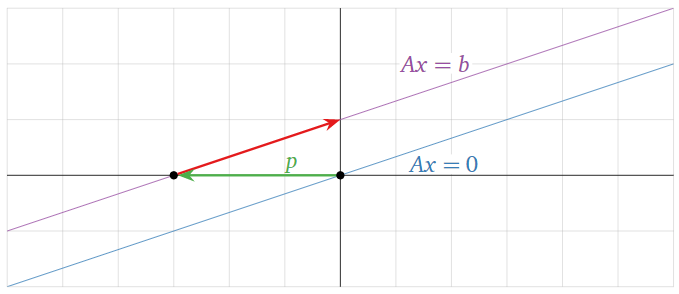
Aquí hay una imagen del conjunto de soluciones:
Figura\(\PageIndex{9}\)
En el Ejemplo anterior\(\PageIndex{6}\), el conjunto de soluciones fueron todos los vectores de la forma
\[x=\left(\begin{array}{c}x_1 \\ x_2 \\ x_3\end{array}\right) =x_2\left(\begin{array}{c}1\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right)+\left(\begin{array}{c}1\\0\\0\end{array}\right).\nonumber\]
donde\(x_2\) y\(x_3\) son los escalares. En este caso, una solución particular es\(p=\left(\begin{array}{c}1\\0\\0\end{array}\right)\).
En el Ejemplo anterior\(\PageIndex{6}\) y en el Ejemplo\(\PageIndex{5}\) anterior, la forma vectorial paramétrica del conjunto de solución de\(Ax=b\) fue exactamente la misma que la forma vectorial paramétrica del conjunto de solución de\(Ax=0\) (de este Ejemplo\(\PageIndex{4}\) y de este Ejemplo\(\PageIndex{3}\), respectivamente), más un solución particular.
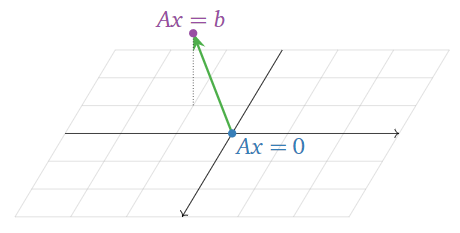
Si\(Ax=b\) es consistente, el conjunto de soluciones a se obtiene tomando una solución\(p\) particular\(Ax=b\text{,}\) y agregando todas las soluciones de\(Ax=0\).
En particular, si\(Ax=b\) es consistente, el conjunto de soluciones es una traducción de un span.
La forma vectorial paramétrica de las soluciones de\(Ax=b\) es solo la forma vectorial paramétrica de las soluciones de\(Ax=0\text{,}\) más una solución particular\(p\).
No es difícil ver por qué la observación clave\(\PageIndex{3}\) es cierta. Si\(p\) es una solución particular, entonces\(Ap=b\text{,}\) y si\(x\) es una solución a la ecuación homogénea\(Ax=0\text{,}\) entonces
\[ A(x+p) = Ax + Ap = 0 + b = b, \nonumber \]
así\(x+p\) es otra solución de\(Ax=b\). Por otro lado, si empezamos con alguna solución\(x\) para\(Ax=b\) entonces\(x-p\) es una solución a\(Ax=0\) desde
\[ A(x-p)=Ax-Ap=b-b=0\text{.} \nonumber \]
La reducción de filas para encontrar la forma vectorial paramétrica le dará una solución particular\(p\) de\(Ax=b\). Pero la observación clave\(\PageIndex{3}\) es cierta para cualquier solución\(p\). Es decir, si remonamos reducimos de una manera diferente y encontramos una solución diferente\(p'\) para\(Ax=b\) entonces las soluciones a se\(Ax=b\) pueden obtener de las soluciones a ya sea\(Ax=0\) agregando\(p\) o agregando\(p'\).
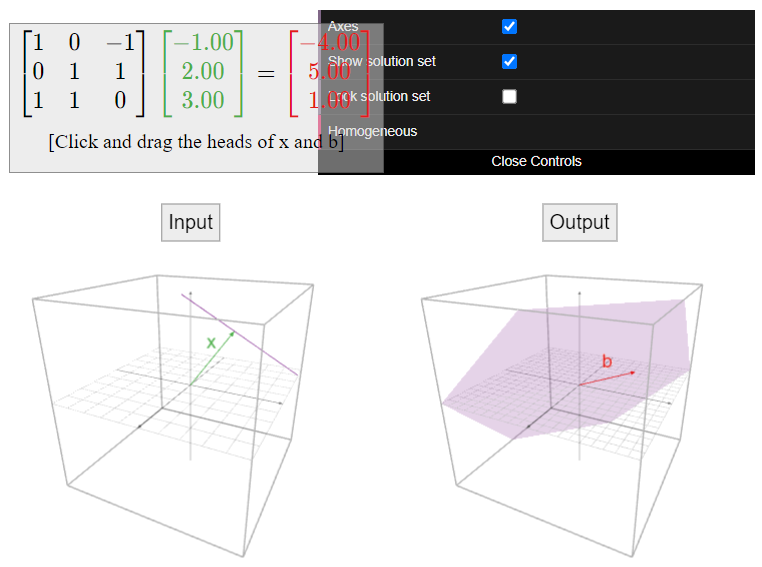
¿Cuál es el conjunto de soluciones de\(Ax=b\text{,}\) dónde
\[A=\left(\begin{array}{c}1&3&4\\2&-1&2 \\ 1&0&1\end{array}\right)\quad\text{and}\quad b=\left(\begin{array}{c}0\\1\\0\end{array}\right)?\nonumber\]
Solución
Formamos una matriz aumentada y la fila reducimos:
\[\left(\begin{array}{ccc|c} 1&3&4&0 \\ 2&-1&2&1 \\ 1&0&1&0\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{ccc|c} 1&0&0&-1 \\ 0&1&0&-1 \\ 0&0&1&1\end{array}\right).\nonumber\]
La única solución es\(p=\left(\begin{array}{c}-1\\-1\\1\end{array}\right)\).
Según la observación clave\(\PageIndex{3}\), se supone que esto es un traducir de un lapso por\(p\). En efecto, vimos en el primer Ejemplo\(\PageIndex{1}\) que la única solución de\(Ax=0\) es la solución trivial, es decir, que el conjunto de soluciones es el conjunto de un punto\(\{0\}\). El conjunto de soluciones de la ecuación no homogénea\(Ax=b\) es
\[\{0\}+\left(\begin{array}{c}-1\\-1\\1\end{array}\right).\nonumber\]
Tenga en cuenta que\(\{0\} = \text{Span}\{0\}\text{,}\) así el conjunto de soluciones homogéneas es un lapso.
Figura\(\PageIndex{11}\)
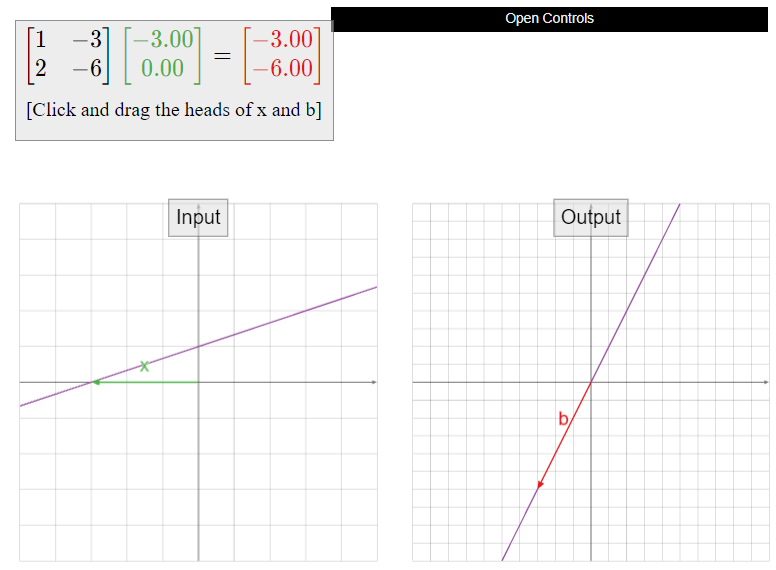
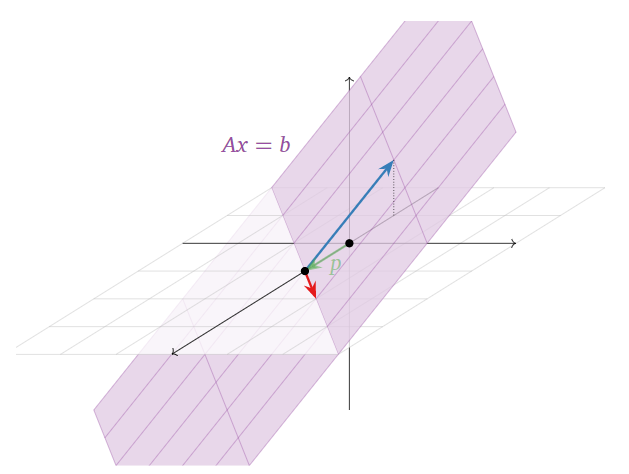
Consulte las figuras interactivas en la siguiente subsección Conjuntos de soluciones y vanos de columna para visualizaciones de la observación clave\(\PageIndex{3}\).
Como en esta nota importante, cuando hay una variable libre en una ecuación matricial consistente, el conjunto de soluciones es una línea —esta línea no pasa por el origen cuando el sistema es inhomogéneo— cuando hay dos variables libres, el conjunto de soluciones es un plano (de nuevo no a través del origen cuando el sistema está no homogéneo), etc.
Nuevamente compare con esta importante nota en la Sección 2.5, Nota 2.5.5.
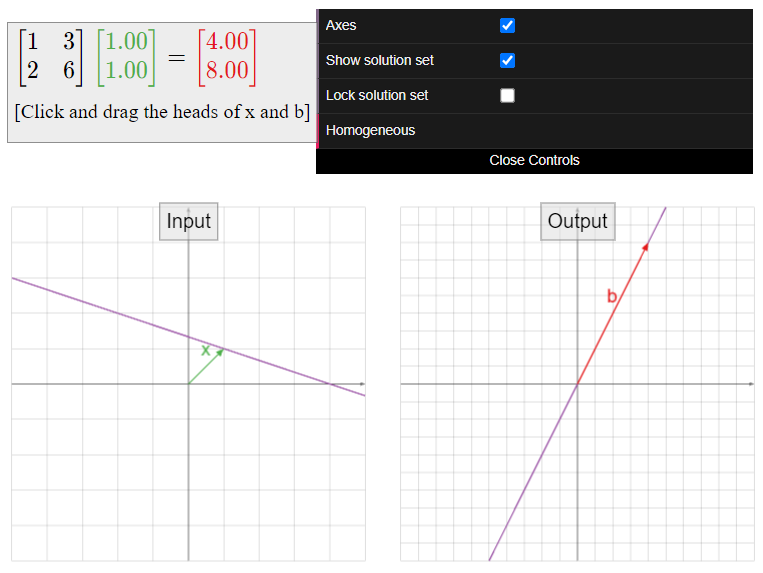
Conjuntos de soluciones y vanos de columna
A cada\(m\times n\) matriz\(A\text{,}\) hemos asociado ahora dos objetos geométricos completamente diferentes, ambos descritos usando vanos.
- El conjunto de soluciones: para fijo\(b\text{,}\) este es el conjunto de todos\(x\) tales que\(Ax=b\).
- Este es un span if\(b=0\text{,}\) y es un translate de un span if\(b\neq 0\) (y\(Ax=b\) es consistente).
- Es un subconjunto de\(\mathbb{R}^n\).
- Se calcula resolviendo un sistema de ecuaciones: generalmente reduciendo filas y encontrando la forma vectorial paramétrica.
- El lapso de las columnas de\(A\): este es el conjunto de todos los\(b\) tales que\(Ax=b\) es consistente.
- Esto siempre es un lapso.
- Es un subconjunto de\(\mathbb{R}^m\).
- No se calcula resolviendo un sistema de ecuaciones: la reducción de filas no juega ningún papel.
¡No confundas estas dos construcciones geométricas! En la primera la pregunta es cuál\(x\) es trabajo para un dado\(b\) y en la segunda la pregunta es cuál\(b\) es trabajo para algunos\(x\).