2.5: Independencia lineal
- Page ID
- 113041
- Comprender el concepto de independencia lineal.
- Aprender dos criterios para la independencia lineal.
- Comprender la relación entre independencia lineal y columnas pivotantes/variables libres.
- Receta: probar si un conjunto de vectores es linealmente independiente/encontrar una ecuación de dependencia lineal.
- Imagen: si un conjunto de vectores en\(\mathbb{R}^2\) o\(\mathbb{R}^3\) es linealmente independiente o no.
- Palabras de vocabulario: relación de dependencia lineal/ecuación de dependencia lineal.
- Palabras esenciales del vocabulario: linealmente independiente, linealmente dependiente.
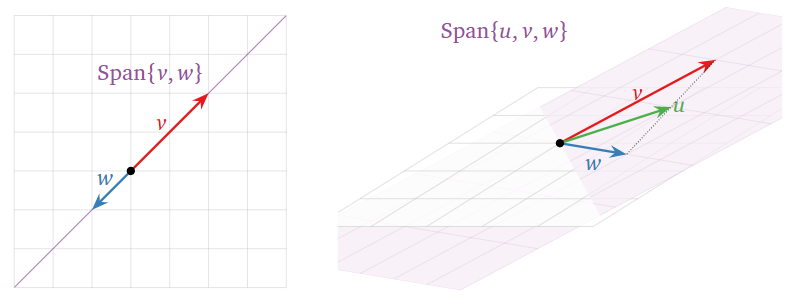
A veces el lapso de un conjunto de vectores es “menor” de lo que esperas del número de vectores, como en la imagen de abajo. Esto significa que (al menos) uno de los vectores es redundante: se puede eliminar sin afectar el span. En la presente sección formalizamos esta idea en la noción de independencia lineal.

La definición de independencia lineal
Un conjunto de vectores\(\{v_1,v_2,\ldots,v_k\}\) es linealmente independiente si la ecuación vectorial
\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = 0 \nonumber \]
tiene sólo la solución trivial\(x_1=x_2=\cdots=x_k=0\). El conjunto\(\{v_1,v_2,\ldots,v_k\}\) es linealmente dependiente de lo contrario.
En otras palabras,\(\{v_1,v_2,\ldots,v_k\}\) es linealmente dependiente si existen números\(x_1,x_2,\ldots,x_k\text{,}\) no todos iguales a cero, tal que
\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = 0. \nonumber \]
Esto se denomina relación de dependencia lineal o ecuación de dependencia lineal.
Tenga en cuenta que la dependencia lineal y la independencia lineal son nociones que se aplican a una colección de vectores. No tiene sentido decir cosas como “este vector depende linealmente de estos otros vectores”, o “esta matriz es linealmente independiente”.
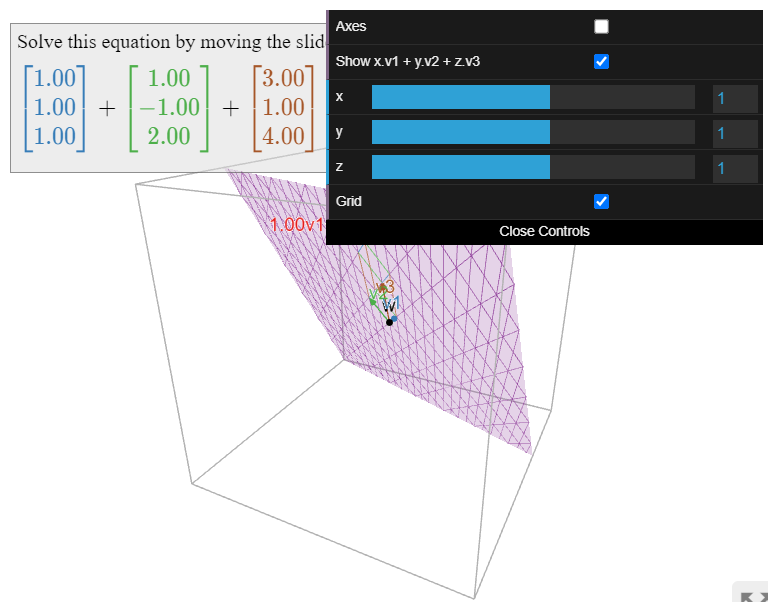
Es el conjunto
\[\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\left(\begin{array}{c}1\\-1\\2\end{array}\right),\:\left(\begin{array}{c}3\\1\\4\end{array}\right)\right\}\nonumber\]
linealmente independiente?
Solución
Equivalentemente, estamos preguntando si la ecuación vectorial homogénea
\[x\left(\begin{array}{c}1\\1\\1\end{array}\right)+y\left(\begin{array}{c}1\\-1\\2\end{array}\right)+x\left(\begin{array}{c}3\\1\\4\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right)\nonumber\]
tiene una solución no trivial. Esto lo resolvemos formando una matriz y una reducción de filas (no aumentamos debido a esta Observación 2.4.2 en la Sección 2.4):
\[\left(\begin{array}{ccc}1&1&3 \\ 1&-1&1 \\ 1&2&4\end{array}\right) \quad\xrightarrow{\text{row reduce}}\quad \left(\begin{array}{ccc}1&0&2 \\ 0&1&1 \\ 0&0&0\end{array}\right)\nonumber\]
Esto dice\(x = -2z\) y\(y = -z\). Entonces existen soluciones no triviales: por ejemplo, tomar\(z=1\) da esta ecuación de dependencia lineal:
\[-2\left(\begin{array}{c}1\\1\\1\end{array}\right)-\left(\begin{array}{c}1\\-1\\2\end{array}\right)+\left(\begin{array}{c}3\\1\\4\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]
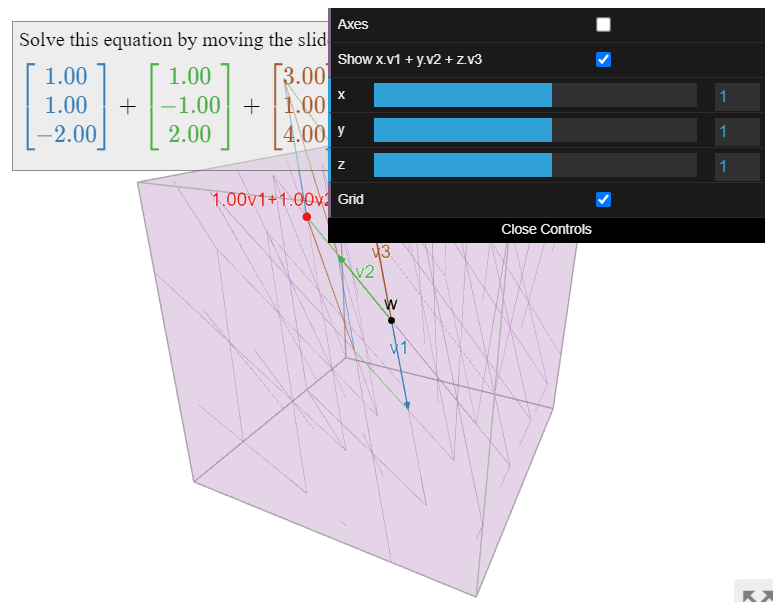
Es el conjunto
\[\left\{\left(\begin{array}{c}1\\1\\-2\end{array}\right),\:\left(\begin{array}{c}1\\-1\\2\end{array}\right),\:\left(\begin{array}{c}3\\1\\4\end{array}\right)\right\}\nonumber\]
linealmente independiente?
Solución
Equivalentemente, estamos preguntando si la ecuación vectorial homogénea
\[x\left(\begin{array}{c}1\\1\\-2\end{array}\right)+y\left(\begin{array}{c}1\\-1\\2\end{array}\right)+z\left(\begin{array}{z}3\\1\\4\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right)\nonumber\]
tiene una solución no trivial. Esto lo resolvemos formando una matriz y una reducción de filas (no aumentamos debido a esta Observación 2.4.2 en la Sección 2.4):
\[\left(\begin{array}{ccc}1&1&3 \\ 1&-1&1 \\ -2&2&4\end{array}\right) \quad\xrightarrow{\text{row reduce}}\quad \left(\begin{array}{ccc}1&0&0 \\ 0&1&0 \\ 0&0&1\end{array}\right)\nonumber\]
Esto dice\(x = y = z = 0\text{,}\) i.e., la única solución es la solución trivial. Se concluye que el conjunto es linealmente independiente.
Una observación importante es que los vectores que provienen de la forma vectorial paramétrica de la solución de una ecuación matricial\(Ax=0\) son linealmente independientes. En el Ejemplo 2.4.4 vimos que el conjunto de soluciones de\(Ax=0\) for
\[A=\left(\begin{array}{ccc}1&-1&2 \\ -2&2&-4\end{array}\right)?\nonumber\]
es
\[x=\left(\begin{array}{c}x_1 \\ x_2 \\ x_3\end{array}\right) =x_2\left(\begin{array}{c}1\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right).\nonumber\]
Vamos a explicar por qué los vectores\((1,1,0)\) y\((-2,0,1)\) son linealmente independientes. Supongamos que
\[\left(\begin{array}{c}0\\0\\0\end{array}\right) =x_2\left(\begin{array}{c}1\\1\\0\end{array}\right) +x_3\left(\begin{array}{c}-2\\0\\1\end{array}\right) =\left(\begin{array}{c} x_2 -2x_3 \\ x_2 \\ x_3\end{array}\right).\nonumber\]
Comparando las coordenadas segunda y tercera, vemos eso\(x_2=x_3=0\). Este razonamiento funcionará en cualquier ejemplo, ya que las entradas correspondientes a las variables libres son todas iguales a 1 o 0, y solo son iguales a 1 en uno de los vectores. Esta observación forma parte de este teorema en la Sección 2.7, Teorema 2.7.2.
Los ejemplos anteriores llevan a la siguiente receta.
Un conjunto de vectores\(\{v_1,v_2,\ldots,v_k\}\) es linealmente independiente si y solo si la ecuación vectorial
\[ x_1v_1 + x_2v_2 + \cdots + x_kv_k = 0 \nonumber \]
tiene solo la solución trivial, si y solo si la ecuación matricial\(Ax=0\) tiene solo la solución trivial, donde\(A\) está la matriz con columnas\(v_1,v_2,\ldots,v_k\text{:}\)
\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 & v_2 &\cdots &v_k \\ |&|&\quad &|\end{array}\right).\nonumber\]
Esto es cierto si y solo si\(A\) tiene una posición de pivote, Definición 1.2.5 en la Sección 1.2 en cada columna.
Resolver la ecuatión matricial\(Ax=0\) verificará que las columnas\(v_1,v_2,\ldots,v_k\) son linealmente independientes, o producirá una relación de dependencia lineal sustituyendo cualquier valor distinto de cero por las variables libres.
(Recordemos que\(Ax=0\) tiene una solución no trivial si y sólo si\(A\) tiene una columna sin pivote: ver esta Observación 2.4.1 en la Sección 2.4.)
Supongamos que\(A\) tiene más columnas que filas. Entonces\(A\) no puede tener un pivote en cada columna (tiene como máximo un pivote por fila), por lo que sus columnas son automáticamente dependientes linealmente.
Una matriz ancha (una matriz con más columnas que filas) tiene columnas linealmente dependientes.
Por ejemplo, cuatro vectores en\(\mathbb{R}^3\) son automáticamente dependientes linealmente. Tenga en cuenta que una matriz alta puede tener o no columnas linealmente independientes.
- Dos vectores son linealmente dependientes si y solo si son colineales, es decir, uno es un múltiplo escalar del otro.
- Cualquier conjunto que contenga el vector cero es linealmente dependiente.
- Si un subconjunto de\(\{v_1,v_2,\ldots,v_k\}\) es linealmente dependiente, entonces también\(\{v_1,v_2,\ldots,v_k\}\) es linealmente dependiente.
- Prueba
-
- Si\(v_1 = cv_2\) entonces\(v_1-cv_2=0\text{,}\) así\(\{v_1,v_2\}\) es linealmente dependiente. En la otra dirección, si\(x_1v_1+x_2v_2=0\) con\(x_1\neq0\) (digamos), entonces\(v_1 = -\frac{x_2}{x_1}v_2\).
- Es fácil producir una relación de dependencia lineal si un vector es el vector cero: por ejemplo, si\(v_1=0\) entonces
\[ 1\cdot v_1 + 0\cdot v_2 + \cdots + 0\cdot v_k = 0. \nonumber \] - Después de reordenar, podemos suponer que\(\{v_1,v_2,\ldots,v_r\}\) es linealmente dependiente, con\(r < p\). Esto significa que existe una ecuación de dependencia lineal\[ x_1v_1 + x_2v_2 + \cdots + x_rv_r = 0\text{,} \nonumber \] con al menos una de distinta de\(x_1,x_2,\ldots,x_r\) cero. Esta también es una ecuación de dependencia lineal entre\(\{v_1,v_2,\ldots,v_k\}\text{,}\) ya que podemos tomar los coeficientes de\(v_{r+1},\ldots,v_k\) a todos ser cero.
Con respecto al primer hecho, tenga en cuenta que el vector cero es un múltiplo de cualquier vector, por lo que es colineal con cualquier otro vector. De ahí que los hechos 1 y 2 sean consistentes entre sí.
Criterios de Independencia Lineal
En esta subsección damos dos criterios para que un conjunto de vectores sea linealmente independiente. Tenga en cuenta, sin embargo, que la definición real de independencia lineal, Definición\(\PageIndex{1}\), está arriba.
Un conjunto de vectores\(\{v_1,v_2,\ldots,v_k\}\) es linealmente dependiente si y solo si uno de los vectores está en el lapso de los otros.
Cualquier vector de este tipo puede ser eliminado sin afectar el lapso.
- Prueba
-
Supongamos, por ejemplo, que\(v_3\) está en\(\text{Span}\{v_1,v_2,v_4\}\text{,}\) así que tenemos una ecuación como
\[ v_3 = 2v_1 - \frac 12v_2 + 6v_4. \nonumber \]
Podemos subactuar\(v_3\) desde ambos lados de la ecuación para obtener
\[ 0 = 2v_1 - \frac 12v_2 - v_3 + 6v_4. \nonumber \]
Se trata de una relación de dependencia lineal.
En este caso, cualquier combinación lineal de ya\(v_1,v_2,v_3,v_4\) es una combinación lineal de\(v_1,v_2,v_4\text{:}\)
\[\begin{aligned} x_1v_1 + x_2v_2 + x_3v_3 + x_4v_4 &= x_1v_1 + x_2v_2 + x_3\left(2v_1-\frac 12v_2 + 6v_4\right) + x_4v_4\\ &= (x_1+2x_3)v_1 + \left(x_2-\frac 12x_3\right)v_2 + (x_4+6)v_4. \end{aligned}\]
Por lo tanto,\(\text{Span}\{v_1,v_2,v_3,v_4\}\) está contenida en\(\text{Span}\{v_1,v_2,v_4\}\). Cualquier combinación lineal de también\(v_1,v_2,v_4\) es una combinación lineal de\(v_1,v_2,v_3,v_4\) (con el\(v_3\) coeficiente -igual a cero), por lo que también\(\text{Span}\{v_1,v_2,v_4\}\) está contenida en\(\text{Span}\{v_1,v_2,v_3,v_4\}\text{,}\) y por lo tanto son iguales.
En la otra dirección, si tenemos una relación de dependencia lineal como
\[ 0 = 2v_1 - \frac 12v_2 + v_3 - 6v_4, \nonumber \]
entonces podemos mover cualquier término distinto de cero al lado izquierdo de la ecuación y dividirlo por su coeficiente:
\[ v_1 = \frac 12\left(\frac 12v_2 - v_3 + 6v_4\right). \nonumber \]
Esto demuestra que\(v_1\) está en\(\text{Span}\{v_2,v_3,v_4\}\).
Dejamos al lector generalizar esta prueba para cualquier conjunto de vectores.
En un conjunto linealmente dependiente no\(\{v_1,v_2,\ldots,v_k\}\text{,}\) es generalmente cierto que cualquier vector\(v_j\) esté en el lapso de los demás, sólo que al menos uno de ellos lo esté.
Por ejemplo, el conjunto\(\bigl\{{1\choose 0},\,{2\choose 0},\,{0\choose 1}\bigr\}\) es linealmente dependiente, pero no\({0\choose 1}\) está en el lapso de los otros dos vectores. Vea también esta Figura\(\PageIndex{14}\) a continuación.
El Teorema\(\PageIndex{1}\) anterior precisa en qué sentido un conjunto de vectores linealmente dependientes es redundante.
Un conjunto de vectores\(\{v_1,v_2,\ldots,v_k\}\) es linealmente independiente si y solo si, para cada uno\(j\text{,}\) el vector no\(v_j\) está en\(\text{Span}\{v_1,v_2,\ldots,v_{j-1}\}\).
- Prueba
-
Es equivalente a mostrar que\(\{v_1,v_2,\ldots,v_k\}\) es linealmente dependiente si y sólo si\(v_j\) está en\(\text{Span}\{v_1,v_2,\ldots,v_{j-1}\}\) para algunos\(j\). La implicación “si” es una consecuencia inmediata del Teorema anterior\(\PageIndex{1}\). Supongamos entonces que\(\{v_1,v_2,\ldots,v_k\}\) es linealmente dependiente. Esto quiere decir\(v_j\) que algunos están en el lapso de los otros. Elija el más grande de este tipo\(j\). Afirmamos que esto\(v_j\) está en\(\text{Span}\{v_1,v_2,\ldots,v_{j-1}\}\). Si no, entonces
\[ v_j = x_1v_1 + x_2v_2 + \cdots + x_{j-1}v_{j-1} + x_{j+1}v_{j+1} + \cdots + x_kv_k \nonumber \]
con no todos\(x_{j+1},\ldots,x_k\) iguales a cero. Supongamos que por simplicidad eso\(x_k\neq 0\). Entonces podemos reorganizar:
\[ v_k = -\frac 1{x_k}\bigl( x_1v_1 + x_2v_2 + \cdots + x_{j-1}v_{j-1} - v_j + x_{j+1}v_{j+1} + \cdots + x_{p-1}v_{p-1} \bigr). \nonumber \]
Esto dice que\(v_k\) está en el lapso de\(\{v_1,v_2,\ldots,v_{p-1}\}\text{,}\) lo cual contradice nuestra suposición de que\(v_j\) es el último vector en el lapso de los demás.
Podemos reformularlo de la siguiente manera:
Si haces un conjunto de vectores agregando un vector a la vez, y si el lapso se hizo más grande cada vez que agregaste un vector, entonces tu conjunto es linealmente independiente.
Imágenes de Linear Independence
Un conjunto que contiene un vector\(\{v\}\) es linealmente independiente cuando\(v\neq 0\text{,}\) ya\(xv = 0\) implica\(x=0\).
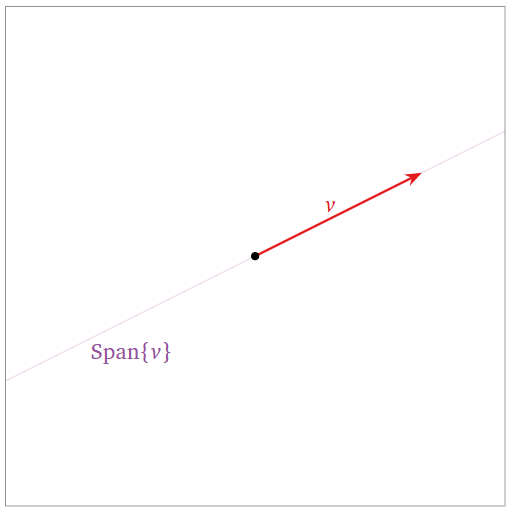
Figura\(\PageIndex{4}\)
Un conjunto de dos vectores no colineales\(\{v,w\}\) es linealmente independiente:
- Tampoco está en el lapso del otro, por lo que podemos aplicar el primer criterio, el Teorema\(\PageIndex{1}\).
- El span se hizo más grande cuando agregamos\(w\text{,}\) así podemos aplicar el criterio de span creciente, Teorema\(\PageIndex{2}\).
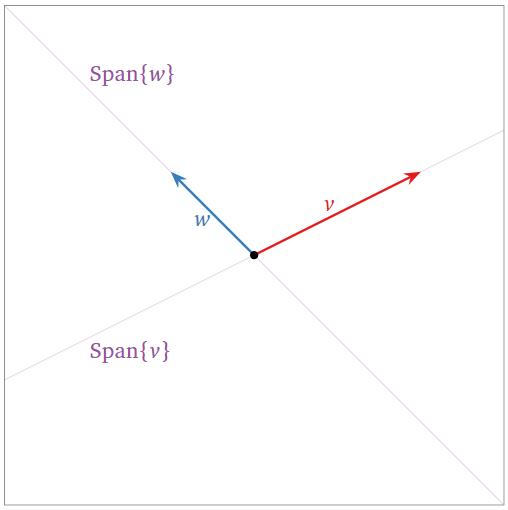
Figura\(\PageIndex{5}\)
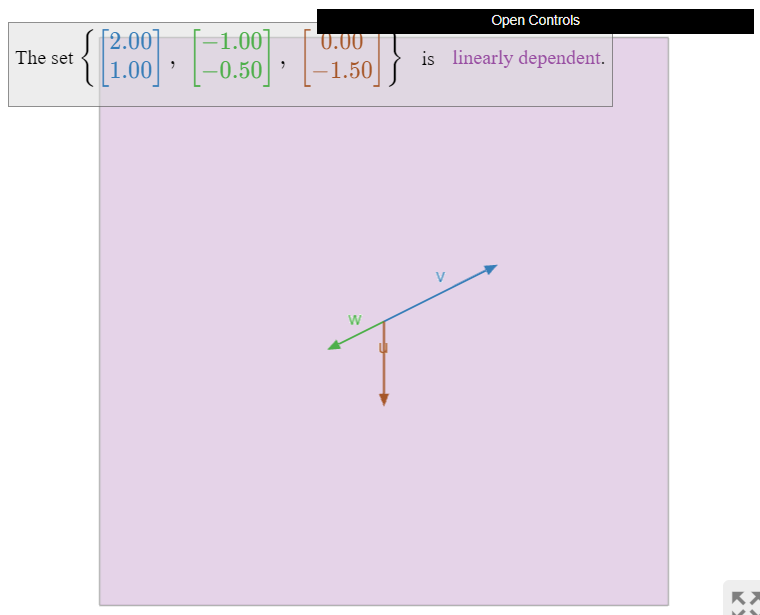
El conjunto de tres vectores\(\{v,w,u\}\) a continuación es linealmente dependiente:
- \(u\)está en\(\text{Span}\{v,w\}\text{,}\) lo que podemos aplicar el primer criterio, Teorema\(\PageIndex{1}\).
- El lapso no aumentó cuando agregamos\(u\text{,}\) por lo que podemos aplicar el criterio de span creciente, Teorema\(\PageIndex{2}\).
En la imagen de abajo, tenga en cuenta que\(v\)\(w\) está en\(\text{Span}\{u,w\}\text{,}\) y está en\(\text{Span}\{u,v\}\text{,}\) para que podamos eliminar cualquiera de los tres vectores sin reducir el span.
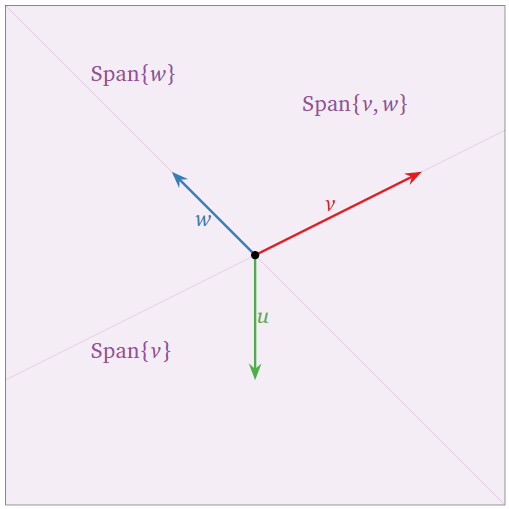
Figura\(\PageIndex{6}\)
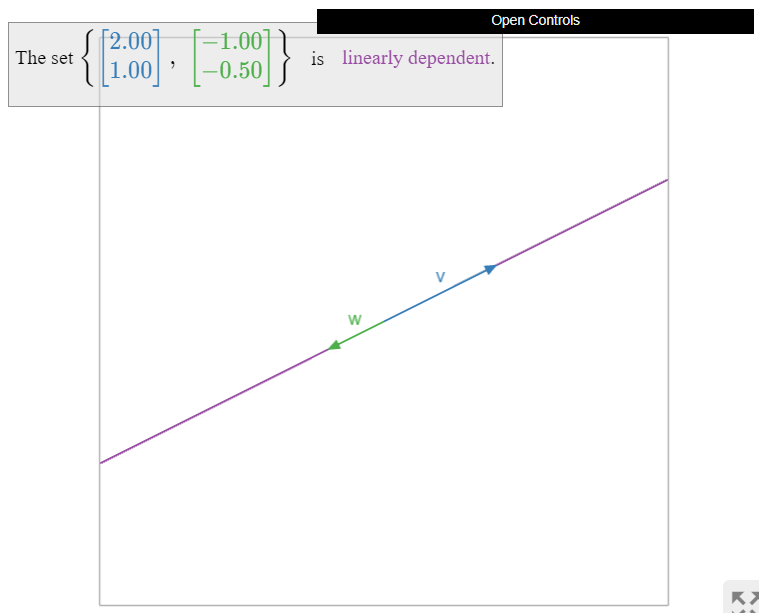
Dos vectores colineales son siempre linealmente dependientes:
- \(w\)está en\(\text{Span}\{v\}\text{,}\) lo que podemos aplicar el primer criterio, Teorema\(\PageIndex{1}\).
- El lapso no aumentó cuando agregamos\(w\text{,}\) por lo que podemos aplicar el criterio de span creciente, Teorema\(\PageIndex{2}\).
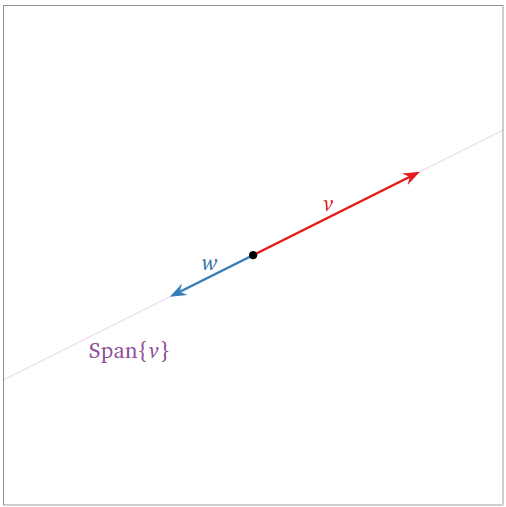
Figura\(\PageIndex{7}\)
Estos tres vectores\(\{v,w,u\}\) son linealmente dependientes: en efecto, ya\(\{v,w\}\) es linealmente dependiente, por lo que podemos usar el tercer Hecho\(\PageIndex{1}\).
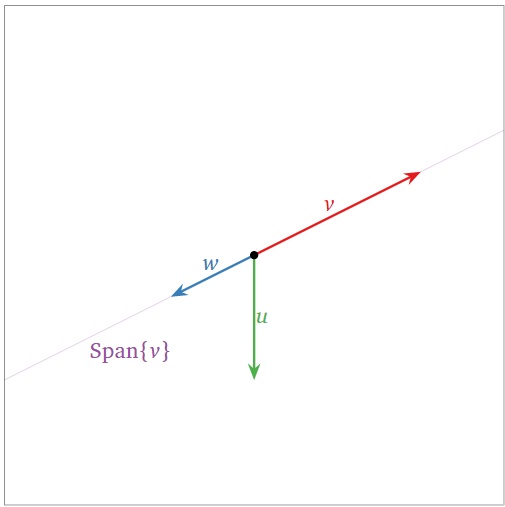
Figura\(\PageIndex{8}\)
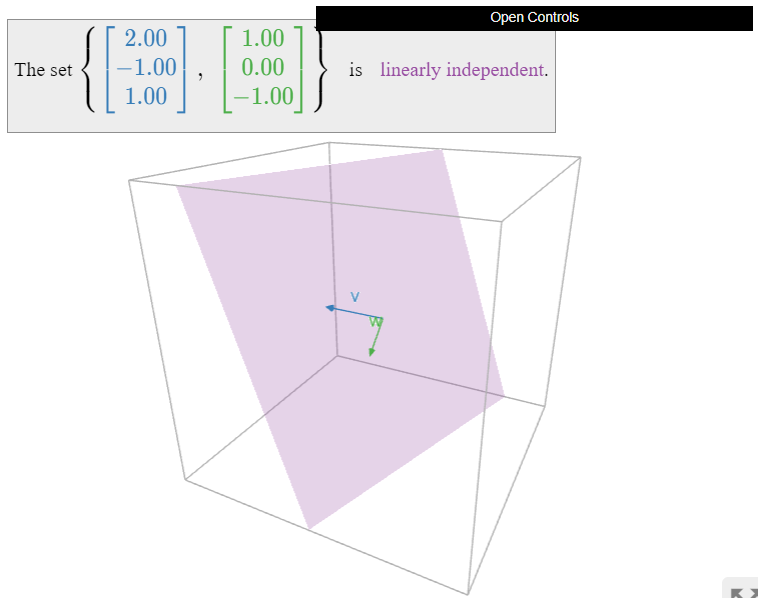
Los dos vectores\(\{v,w\}\) siguientes son linealmente independientes porque no son colineales.
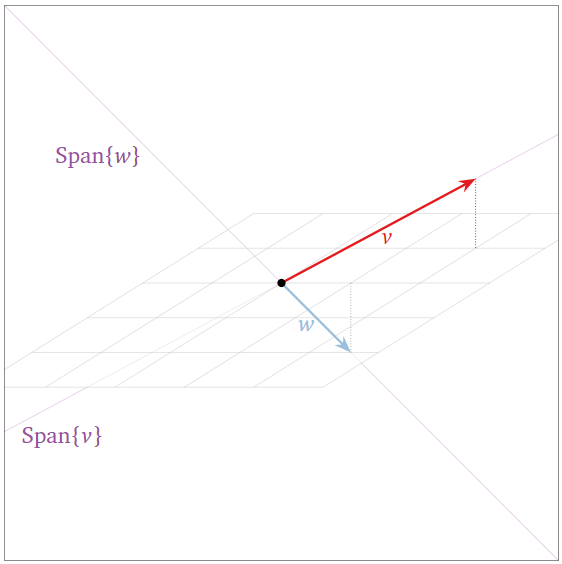
Figura\(\PageIndex{11}\)
Los tres vectores\(\{v,w,u\}\) a continuación son linealmente independientes: el span se hizo más grande cuando agregamos\(w\text{,}\) luego nuevamente cuando agregamos\(u\text{,}\) para que podamos aplicar el criterio de span creciente, Teorema\(\PageIndex{2}\).
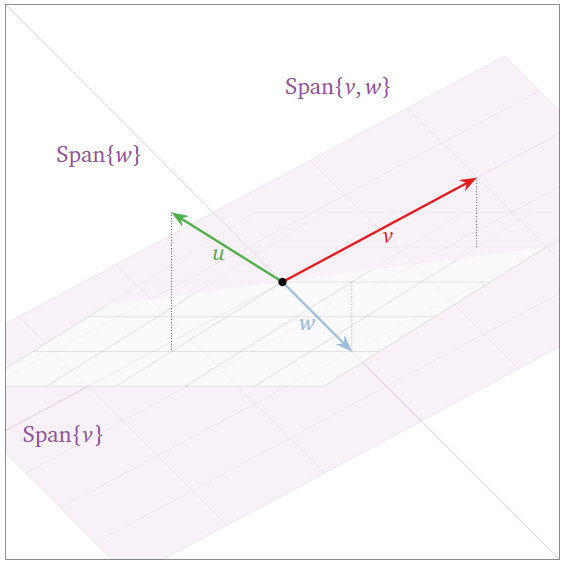
Figura\(\PageIndex{12}\)
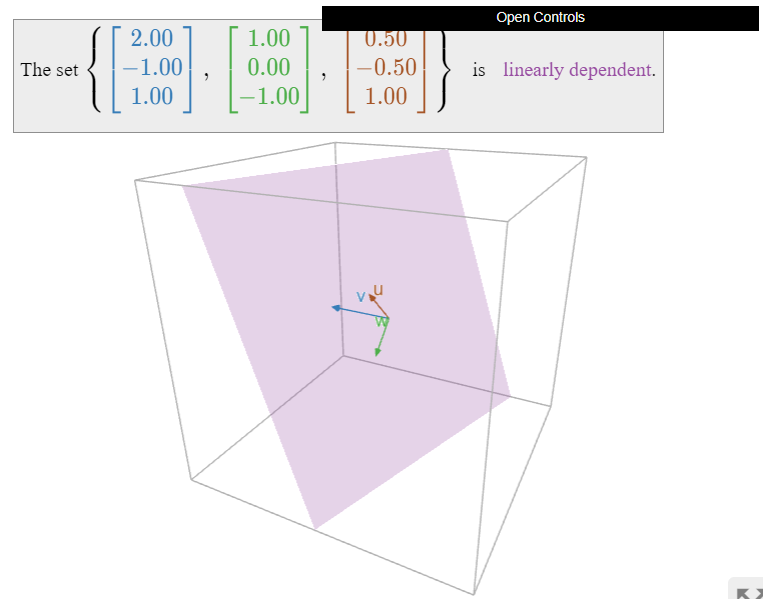
Los tres vectores coplanarios\(\{v,w,u\}\) a continuación son linealmente dependientes:
- \(u\)está en\(\text{Span}\{v,w\}\text{,}\) lo que podemos aplicar el primer criterio, Teorema\(\PageIndex{1}\).
- El lapso no aumentó cuando agregamos\(u\text{,}\) por lo que podemos aplicar el criterio de span creciente, Teorema\(\PageIndex{2}\).
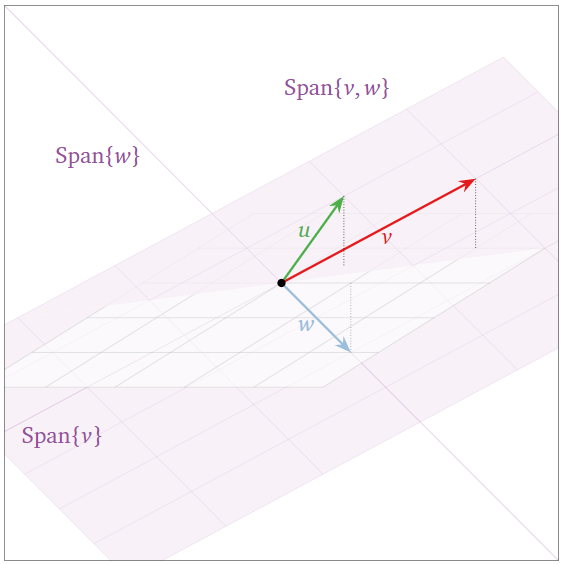
Figura\(\PageIndex{13}\)
Obsérvese que tres vectores son linealmente dependientes si y sólo si son coplanares. En efecto,\(\{v,w,u\}\) es linealmente dependiente si y sólo si un vector está en el lapso de los otros dos, que es un plano (o una línea) (o\(\{0\}\)).
Los cuatro vectores\(\{v,w,u,x\}\) a continuación son linealmente dependientes: son las columnas de una matriz ancha, ver Nota\(\PageIndex{2}\). Tenga en cuenta sin embargo que no\(u\) está contenido en\(\text{Span}\{v,w,x\}\). Ver esta advertencia, Nota\(\PageIndex{3}\).
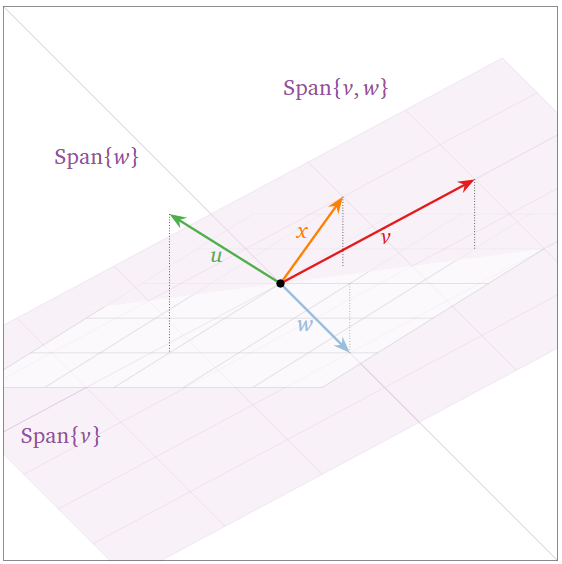

Dependencia Lineal y Variables Libres
A la luz de esta importante nota, Receta: Comprobando Independencia Lineal, y este criterio, Teorema\(\PageIndex{1}\), es natural preguntar qué columnas de una matriz son redundantes, es decir, cuáles podemos eliminar sin afectar el lapso de columna.
Dejar\(v_1,v_2,\ldots,v_k\) ser vectores en\(\mathbb{R}^n\text{,}\) y considerar la matriz
\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots &v_k \\ |&|&\quad &|\end{array}\right).\nonumber\]
Entonces podemos eliminar las columnas de\(A\) sin pivotes (las columnas correspondientes a las variables libres), sin cambiar\(\text{Span}\{v_1,v_2,\ldots,v_k\}\).
Las columnas pivotantes son linealmente independientes, por lo que no podemos eliminar más columnas sin cambiar el span.
- Prueba
-
Si la matriz está en forma de escalón de fila reducida:
\[A=\left(\begin{array}{cccc}1&0&2&0 \\ 0&1&3&0 \\ 0&0&0&1\end{array}\right)\nonumber\]
entonces la columna sin pivote está visiblemente en el tramo de las columnas pivotes:
\[\left(\begin{array}{c}2\\3\\0\end{array}\right)=2\left(\begin{array}{c}1\\0\\0\end{array}\right)+3\left(\begin{array}{c}0\\1\\0\end{array}\right)+0\left(\begin{array}{c}0\\0\\1\end{array}\right),\nonumber\]
y las columnas pivotes son linealmente independientes:
\[\left(\begin{array}{c}0\\0\\0\end{array}\right) =x_1\left(\begin{array}{c}1\\0\\0\end{array}\right)+x_2\left(\begin{array}{c}0\\1\\0\end{array}\right)+x_4\left(\begin{array}{c}0\\0\\1\end{array}\right)=\left(\begin{array}{c}x_1 \\x_2 \\ x_4\end{array}\right)\implies x_1 =x_2 =x_4 =0.\nonumber\]
Si la matriz no está en forma de escalón de fila reducida, entonces remaremos reducir:
\[A=\left(\begin{array}{cccc}1&7&23&3 \\ 2&4&16&0 \\ -1&-2&-8&4\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cccc}1&0&2&0 \\ 0&1&3&0 \\ 0&0&0&1\end{array}\right).\nonumber\]
Las siguientes dos ecuaciones vectoriales tienen el mismo conjunto de soluciones, ya que provienen de matrices equivalentes a filas:
\[\begin{aligned} x_1\left(\begin{array}{c}1\\2\\-1\end{array}\right)+x_2\left(\begin{array}{c}7\\4\\-2\end{array}\right)+x_3\left(\begin{array}{c}23\\16\\-8\end{array}\right)+x_4\left(\begin{array}{c}3\\0\\4\end{array}\right)&=0 \\ x_1\left(\begin{array}{c}1\\0\\0\end{array}\right)+x_2\left(\begin{array}{c}0\\1\\0\end{array}\right)+x_3\left(\begin{array}{c}2\\3\\0\end{array}\right)+x_4\left(\begin{array}{c}0\\0\\1\end{array}\right)&=0\end{aligned}\]
Concluimos que
\[\left(\begin{array}{c}23\\16\\-8\end{array}\right)=2\left(\begin{array}{c}1\\2\\-1\end{array}\right)+3\left(\begin{array}{c}7\\4\\-2\end{array}\right)+0\left(\begin{array}{c}3\\0\\4\end{array}\right)\nonumber\]
y que
\[x_1\left(\begin{array}{c}1\\2\\-1\end{array}\right)+x_2\left(\begin{array}{c}7\\4\\-2\end{array}\right)+x_4\left(\begin{array}{c}3\\0\\4\end{array}\right)=0\nonumber\]
tiene sólo la solución trivial.
Tenga en cuenta que es necesario remar reducir\(A\) para encontrar cuáles son sus columnas pivotantes, Definición 1.2.5 en la Sección 1.2. Sin embargo, el lapso de las columnas de la matriz de fila reducida generalmente no es igual al lapso de las columnas de\(A\text{:}\) uno debe usar las columnas pivotantes de la matriz original. Véase teorema en la Sección 2.7, Teorema 2.7.2 para una reafirmación del teorema anterior.
La matriz
\[A=\left(\begin{array}{cccc}1&2&0&-1 \\ -2&-3&4&5 \\ 2&4&0&-2\end{array}\right)\nonumber\]
tiene forma de escalón de fila reducida
\[\left(\begin{array}{cccc}1&0&-8&-7 \\ 0&1&4&3 \\ 0&0&0&0\end{array}\right).\nonumber\]
Por lo tanto, las dos primeras columnas de\(A\) son las columnas pivotantes, por lo que podemos eliminar las otras sin cambiar el span:
\[\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right)\right\}=\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right),\:\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}.\nonumber\]
Además, las dos primeras columnas son linealmente independientes.
Dejar\(d\) ser el número de columnas pivotes en la matriz
\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots &v_k \\ |&|&\quad &| \end{array}\right).\nonumber\]
- Si\(d=1\) entonces\(\text{Span}\{v_1,v_2,\ldots,v_k\}\) es una línea.
- Si\(d=2\) entonces\(\text{Span}\{v_1,v_2,\ldots,v_k\}\) es un avión.
- Si\(d=3\) entonces\(\text{Span}\{v_1,v_2,\ldots,v_k\}\) es un espacio de 3.
- etcétera.
El número\(d\) se llama la dimensión. Discutimos esta noción en esta nota importante en la Sección 2.4, Nota 2.4.4 y esta nota importante en la Sección 2.4, Nota 2.4.5. Definiremos este concepto rigurosamente en la Sección 2.7.