2.6: Subespacios
- Page ID
- 113032
- Aprender la definición de un subespacio.
- Aprende a determinar si un subconjunto es o no un subespacio.
- Conoce los ejemplos más importantes de subespacios.
- Aprende a escribir un subespacio dado como un espacio de columna o espacio nulo.
- Receta: calcular un conjunto de expansión para un espacio nulo.
- Imagen: si un subconjunto de\(\mathbb{R}^2\) o\(\mathbb{R}^3\) es un subespacio o no.
- Palabras de vocabulario: subespacio, espacio de columna, espacio nulo.
En esta sección se discuten los subespacios de\(\mathbb{R}^n\). Un subespacio resulta ser exactamente lo mismo que un lapso, excepto que no tenemos en mente un conjunto particular de vectores de expansión. Este cambio de perspectiva es bastante útil, ya que es fácil producir subespacios que obviamente no son vanos. Por ejemplo, el conjunto de soluciones de la ecuación\(x + 3y + z = 0\) es un span porque la ecuación es homogénea, pero tendríamos que computar la forma vectorial paramétrica para poder escribirla como span.
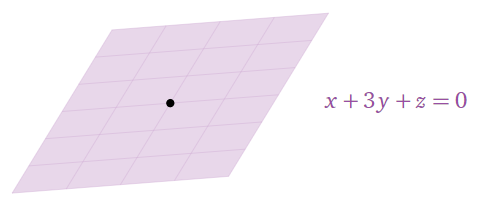
Figura\(\PageIndex{1}\)
(Un subespacio también resulta ser lo mismo que el conjunto de soluciones de un sistema homogéneo de ecuaciones.)
Subespacios: Definición y Ejemplos
Un subconjunto de\(\mathbb{R}^n\) es cualquier colección de puntos de\(\mathbb{R}^n\).
Por ejemplo, el círculo unitario
\[ C = \bigl\{ (x,y)\text{ in }\mathbb{R}^2 \bigm| x^2 + y^2 = 1 \bigr\} \nonumber \]
es un subconjunto de\(\mathbb{R}^2\).
Arriba expresamos\(C\) en notación set builder, Nota 2.2.3 en la Sección 2.2: en inglés, dice “\(C\)es el conjunto de todos los pares ordenados\((x,y)\) en\(\mathbb{R}^2\) tal que”\(x^2+y^2=1\).
Un subespacio de\(\mathbb{R}^n\) es un subconjunto\(V\) de\(\mathbb{R}^n\) satisfactorios:
- No vacío: El vector cero está en\(V\).
- Cierre bajo adición: Si\(u\) y\(v\) están en\(V\text{,}\) entonces también\(u+v\) está en\(V\).
- Cierre bajo multiplicación escalar: Si\(v\) está en\(V\) y\(c\) está en\(\mathbb{R}\text{,}\) entonces también\(cv\) está en\(V\).
Como consecuencia de estas propiedades, vemos:
- Si\(v\) es un vector en\(V\text{,}\) entonces todos los múltiplos escalares de\(v\) están en\(V\) por la tercera propiedad. En otras palabras, la línea a través de cualquier vector distinto de cero en también\(V\) está contenida en\(V\).
- Si\(u,v\) son vectores en\(V\) y\(c,d\) son escalares, entonces también\(cu,dv\) están en\(V\) por la tercera propiedad, así\(cu+dv\) es en\(V\) por la segunda propiedad. Por lo tanto, todo\(\text{Span}\{u,v\}\) está contenido en\(V\)
- Del mismo modo, si\(v_1,v_2,\ldots,v_n\) están todos adentro\(V\text{,}\) entonces\(\text{Span}\{v_1,v_2,\ldots,v_n\}\) está contenido en\(V\). En otras palabras, un subespacio contiene el lapso de cualquier vector en él.
Si eliges suficientes vectores, entonces eventualmente su lapso se llenará\(V\text{,}\) así que ya vemos que un subespacio es un lapso. Consulte este Teorema\(\PageIndex{1}\) a continuación para obtener una declaración precisa.
Supongamos que\(V\) es un subconjunto no vacío del\(\mathbb{R}^n\) que satisface las propiedades 2 y 3. Dejar\(v\) ser cualquier vector en\(V\). Entonces\(0v = 0\) está en\(V\) por la tercera propiedad, por lo que\(V\) automáticamente satisface propiedad 1. De ello se deduce que el único subconjunto\(\mathbb{R}^n \) que satisface las propiedades 2 y 3 pero no la propiedad 1 es el subconjunto vacío\(\{\}\). Es por ello que llamamos a la primera propiedad “no vacío”.
El conjunto\(\mathbb{R}^n\) es un subespacio en sí mismo: en efecto, contiene cero, y se cierra bajo suma y multiplicación escalar.
El conjunto\(\{0\}\) que contiene solo el vector cero es un subespacio del\(\mathbb{R}^n\text{:}\) mismo contiene cero, y si se agrega cero a sí mismo o lo multiplica por un escalar, siempre se obtiene cero.
Una línea que\(L\) atraviesa el origen es un subespacio.
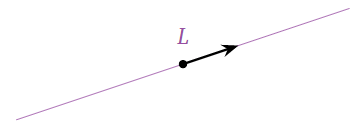
Figura\(\PageIndex{2}\)
En efecto,\(L\) contiene cero, y se ve fácilmente que se cierra bajo suma y multiplicación escalar.
Un plano que\(P\) atraviesa el origen es un subespacio.
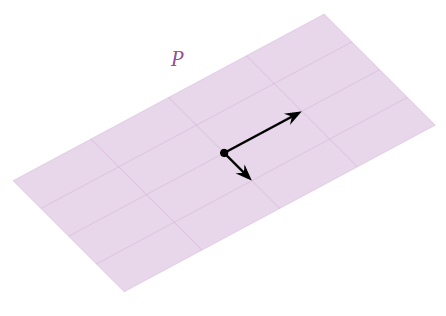
Figura\(\PageIndex{3}\)
De hecho,\(P\) contiene cero; la suma de dos vectores en también\(P\) está adentro\(P\text{;}\) y cualquier múltiplo escalar de un vector en también\(P\) está en\(P\).
Una línea\(L\) (o cualquier otro subconjunto) que no contenga el origen no es un subespacio. Falla la primera propiedad definitoria: cada subespacio contiene el origen por definición.
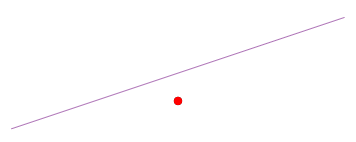
Figura\(\PageIndex{4}\)
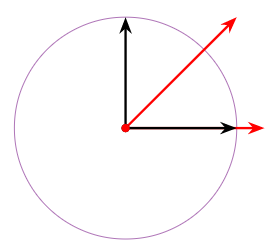
El círculo unitario no\(C\) es un subespacio. Falla las tres propiedades definitorias: no contiene el origen, no se cierra bajo suma, y no se cierra bajo multiplicación escalar. En la imagen, un vector rojo es la suma de los dos vectores negros (que están contenidos en\(C\)), y el otro es un múltiplo escalar de un vector negro.
Figura\(\PageIndex{5}\)
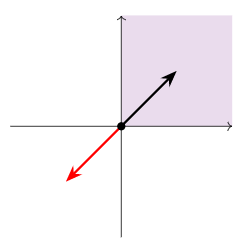
El primer cuadrante en no\(\mathbb{R}^2\) es un subespacio. Contiene el origen y se cierra bajo suma, pero no se cierra bajo multiplicación escalar (por números negativos).
Figura\(\PageIndex{6}\)
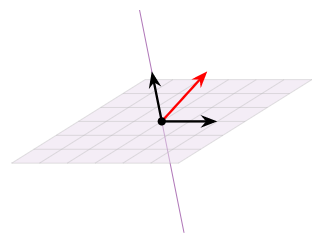
La unión de una línea y un plano en no\(\mathbb{R}^3\) es un subespacio. Contiene el origen y se cierra bajo multiplicación escalar, pero no se cierra bajo suma: la suma de un vector en la línea y un vector en el plano no está contenida en la línea ni en el plano.
Figura\(\PageIndex{7}\)
Un subconjunto de\(\mathbb{R}^n\) es cualquier colección de vectores en absoluto. Por ejemplo, el círculo unitario
\[ C = \bigl\{ (x,y)\text{ in }\mathbb{R}^2 \bigm| x^2 + y^2 = 1 \bigr\} \nonumber \]
es un subconjunto de\(\mathbb{R}^2\text{,}\) pero no es un subespacio. De hecho, todos los no ejemplos anteriores siguen siendo subconjuntos de\(\mathbb{R}^n\). Un subespacio es un subconjunto que satisface las tres propiedades definitorias adicionales.
Para verificar que un subconjunto de\(\mathbb{R}^n\) es de hecho un subespacio, hay que verificar las tres propiedades definitorias. Es decir, a menos que ya se haya verificado que el subconjunto es un subespacio: vea esta nota importante, Nota\(\PageIndex{3}\), a continuación.
Let
\[V=\left\{\left(\begin{array}{c}a\\b\end{array}\right)\text{ in }\mathbb{R}^{2}|2a=3b\right\}.\nonumber\]
Verificar que\(V\) sea un subespacio.
Solución
Primero señalamos que la condición “\(2a = 3b\)” define si un vector está o no en\(V\text{:}\) eso es, decir\({a\choose b}\) está en\(V\) significa eso\(2a = 3b\). En otras palabras, un vector está en\(V\) si dos veces su primera coordenada es igual a tres veces su segunda coordenada. Entonces por ejemplo,\({3\choose 2}\) y\({1/2\choose 1/3}\) están en\(V\text{,}\) pero no\({2\choose 3}\) es porque\(2\cdot 2\neq 3\cdot 3\).
Comprobemos la primera propiedad. El subconjunto\(V\) contiene el vector cero\({0\choose 0}\text{,}\) porque\(2\cdot 0 = 3\cdot 0\).
A continuación revisamos la segunda propiedad. Para mostrar que\(V\) se cierra bajo suma, tenemos que comprobar que para cualquier vector\(u = {a\choose b}\) y\(v = {c\choose d}\) en\(V\text{,}\) la suma\(u+v\) está en\(V\). Ya que no podemos asumir nada más sobre\(u\) y\(v\text{,}\) debemos tratarlos como incógnitas.
Tenemos
\[\left(\begin{array}{c}a\\b\end{array}\right)+\left(\begin{array}{c}c\\d\end{array}\right)=\left(\begin{array}{c}a+c\\b+d\end{array}\right).\nonumber\]
Decir que\(a+c\choose b+d\) está contenido en\(V\) significa que\(2(a+c) = 3(b+d)\text{,}\) o\(2a + 2c = 3b + 3d\). De lo único que se nos permite asumir\(u\) y\(v\) es eso\(2a = 3b\) y\(2c = 3d\text{,}\) así vemos que efectivamente\(u+v\) está contenido en\(V\).
A continuación verificamos la tercera propiedad. Para mostrar que\(V\) se cierra bajo multiplicación escalar, tenemos que verificar que para cualquier vector\(v = {a\choose b}\) en\(V\) y cualquier escalar\(c\) en\(\mathbb{R}\text{,}\) el producto\(cv\) está en\(V\). Nuevamente, debemos tratar\(v\) y\(c\) como incógnitas. Tenemos
\[c\left(\begin{array}{c}a\\b\end{array}\right)=\left(\begin{array}{c}ca\\cb\end{array}\right).\nonumber\]
Decir que\(ca\choose cb\) está contenido en\(V\) significa que\(2(ca) = 3(cb)\text{,}\) es decir, eso\(c\cdot 2a = c\cdot 3b\). De lo único que se nos permite asumir\(v\) es que\(2a = 3b\text{,}\) así\(cv\) está efectivamente contenido en\(V\).
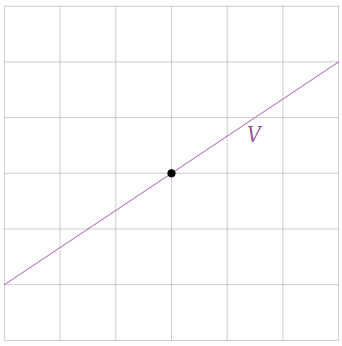
Dado que\(V\) satisface las tres propiedades definitorias, es un subespacio. De hecho, es la línea que atraviesa el origen con pendiente\(2/3\).
Figura\(\PageIndex{8}\)
Let
\[V=\left\{\left(\begin{array}{c}a\\b\end{array}\right)\text{ in }\mathbb{R}^{2}|ab=0\right\}.\nonumber\]
¿Es\(V\) un subespacio?
Solución
Primero señalamos que la condición “\(ab=0\)” define si un vector está o no en\(V\text{:}\) eso es, decir\({a\choose b}\) está en\(V\) significa eso\(ab=0\). En otras palabras, un vector está en\(V\) si el producto de sus coordenadas es cero, es decir, si una (o ambas) de sus coordenadas son cero. Entonces por ejemplo,\({1\choose 0}\) y\({0\choose 2}\) están en\(V\text{,}\) pero no\({1\choose 1}\) es porque\(1\cdot 1\neq 0\).
Comprobemos la primera propiedad. El subconjunto\(V\) contiene el vector cero\({0\choose 0}\text{,}\) porque\(0\cdot 0=0\).
A continuación verificamos la tercera propiedad. Para mostrar que\(V\) se cierra bajo multiplicación escalar, tenemos que verificar que para cualquier vector\(v = {a\choose b}\) en\(V\) y cualquier escalar\(c\) en\(\mathbb{R}\text{,}\) el producto\(cv\) está en\(V\). Ya que no podemos asumir nada más sobre\(v\) y\(c\text{,}\) debemos tratarlos como incógnitas.
Tenemos
\[c\left(\begin{array}{c}a\\b\end{array}\right)=\left(\begin{array}{c}ca\\cb\end{array}\right).\nonumber\]
Decir que\(ca\choose cb\) está contenido en\(V\) significa que\((ca)(cb)=0\). Reescribir, esto significa\(c^2(ab)=0\). De lo único que se nos permite asumir\(v\) es que\(ab=0\text{,}\) así vemos que efectivamente\(cv\) está contenido en\(V\).
A continuación revisamos la segunda propiedad. Resulta que no\(V\) se cierra bajo adición; para verificar esto, debemos demostrar que existen algunos vectores\(u,v\) en\(V\) tal que no\(u+v\) está contenido en\(V\). La forma más fácil de hacerlo es producir ejemplos de tales vectores. Podemos tomar\(u={1\choose 0}\) y\(v={0\choose 1}\text{;}\) estos están contenidos en\(V\) porque los productos de sus coordenadas son cero, pero
\[\left(\begin{array}{c}1\\0\end{array}\right)+\left(\begin{array}{c}0\\1\end{array}\right)=\left(\begin{array}{c}1\\1\end{array}\right)\nonumber\]
no está contenida en\(V\) porque\(1\cdot 1\neq 0\).
Dado que\(V\) no satisface la segunda propiedad (no se cierra bajo suma), concluimos que no\(V\) es un subespacio. En efecto, es la unión de los dos ejes de coordenadas, que no es un tramo.
Figura\(\PageIndex{9}\)
Tipos comunes de subespacios
Si\(v_1,v_2,\ldots,v_p\) hay algún vector en\(\mathbb{R}^n\text{,}\) entonces\(\text{Span}\{v_1,v_2,\ldots,v_p\}\) es un subespacio de\(\mathbb{R}^n\). Además, cualquier subespacio de\(\mathbb{R}^n\) puede escribirse como un lapso de un conjunto de vectores\(p\) linealmente independientes en\(\mathbb{R}^n\) for\(p\leq n\).
- Prueba
-
Para mostrar que\(\text{Span}\{v_1,v_2,\ldots,v_p\}\) es un subespacio, tenemos que verificar las tres propiedades definitorias.
- El vector cero\(0 = 0v_1 + 0v_2 + \cdots + 0v_p\) está en el lapso.
- Si\(u = a_1v_1 + a_2v_2 + \cdots + a_pv_p\) y\(v = b_1v_1 + b_2v_2 + \cdots + b_pv_p\) están en\(\text{Span}\{v_1,v_2,\ldots,v_p\}\text{,}\) entonces también
\[ u + v = (a_1+b_1)v_1 + (a_2+b_2)v_2 + \cdots + (a_p+b_p)v_p \nonumber \]
está en\(\text{Span}\{v_1,v_2,\ldots,v_p\}\). - Si\(v = a_1v_1 + a_2v_2 + \cdots + a_pv_p\) está en\(\text{Span}\{v_1,v_2,\ldots,v_p\}\) y\(c\) es un escalar, entonces también
\[ cv = ca_1v_1 + ca_2v_2 + \cdots + ca_pv_p \nonumber \]
está adentro\(\text{Span}\{v_1,v_2,\ldots,v_p\}\).
Dado que\(\text{Span}\{v_1,v_2,\ldots,v_p\}\) satisface las tres propiedades definitorias de un subespacio, es un subespacio.
Ahora dejemos\(V\) ser un subespacio de\(\mathbb{R}^n\). Si\(V\) es el subespacio cero, entonces es el lapso del conjunto vacío, por lo que podemos suponer que\(V\) es distinto de cero. Elija un vector distinto de cero\(v_1\) en\(V\). Si\(V = \text{Span}\{v_1\}\text{,}\) entonces ya terminamos. De lo contrario, existe un vector\(v_2\) que está en\(V\) pero no en\(\text{Span}\{v_1\}\). Entonces\(\text{Span}\{v_1,v_2\}\) está contenido en\(V\text{,}\) y por el criterio de lapso creciente en la Sección 2.5, Teorema 2.5.2, el conjunto\(\{v_1,v_2\}\) es linealmente independiente. Si\(V = \text{Span}\{v_1,v_2\}\) entonces ya terminamos. De lo contrario, continuamos de esta manera hasta que hayamos escrito\(V = \text{Span}\{v_1,v_2,\ldots,v_p\}\) para algún conjunto linealmente independiente\(\{v_1,v_2,\ldots,v_p\}\). Este proceso termina después de como máximo\(n\) pasos por esta importante nota en la Sección 2.5, Nota 2.5.2.
Si\(V = \text{Span}\{v_1,v_2,\ldots,v_p\}\text{,}\) decimos que\(V\) es el subespacio abarcado por o generado por los vectores\(v_1,v_2,\ldots,v_p\). Llamamos a\(\{v_1,v_2,\ldots,v_p\}\) un conjunto de expansión para\(V\).
Cualquier matriz da lugar naturalmente a dos subespacios.
Dejar\(A\) ser una\(m\times n\) matriz.
- El espacio de columna de\(A\) es el subespacio de\(\mathbb{R}^m\) abarcado por las columnas de\(A\). Está escrito\(\text{Col}(A)\).
- El espacio nulo de\(A\) es el subespacio de\(\mathbb{R}^n\) que consiste en todas las soluciones de la ecuación homogénea\(Ax=0\text{:}\)
\[ \text{Nul}(A) = \bigl\{ x \text{ in } \mathbb{R}^n\bigm| Ax=0 \bigr\}. \nonumber \]
El espacio de columna se define como un span, por lo que es un subespacio por el Teorema anterior, Teorema\(\PageIndex{1}\). Tenemos que verificar que el espacio nulo es realmente un subespacio. En la Sección 2.4 ya vimos que el conjunto de soluciones de\(Ax=0\) es siempre un lapso, por lo que el hecho de que los espacios nulos sean un subespacio no debería ser una sorpresa.
Tenemos que verificar las tres propiedades definitorias. Decir que un vector\(v\) está en\(\text{Nul}(A)\) significa eso\(Av = 0\).
- El vector cero está en\(\text{Nul}(A)\) porque\(A0=0\).
- Supongamos que\(u,v\) están en\(\text{Nul}(A)\). Esto significa que\(Au=0\) y\(Av=0\). De ahí
\[A(u+v)=Au+Av=0+0=0\nonumber\]
por la linealidad del producto matriz-vector en la Sección 2.3, Proposición 2.3.1. Por lo tanto,\(u+v\) is in \(\text{Nul}(A)\). - Supongamos que\(v\) está en\(\text{Nul}(A)\) y\(c\) es un escalar. Luego,
\[A(cv)=cAv=c\cdot 0=0\nonumber\] por la linealidad del producto matriz-vector, la Proposición 2.3 .1 en la Sección 2.3, así\(cv\) is also in \(\text{Nul}(A)\).
Dado que\(\text{Nul}(A)\) satisface las tres propiedades definitorias de un subespacio, es un subespacio.
Describir el espacio de columna y el espacio nulo de
\[A=\left(\begin{array}{cc}1&1\\1&1\\1&1\end{array}\right).\nonumber\]
Solución
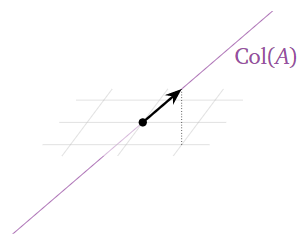
El espacio de columna es el tramo de las columnas de\(A\text{:}\)
\[\text{Col}(A)=\text{Span}\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\left(\begin{array}{c}1\\1\\1\end{array}\right)\right\}=\text{Span}\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right)\right\}.\nonumber\]
Esta es una línea en\(\mathbb{R}^3\).
Figura\(\PageIndex{10}\)
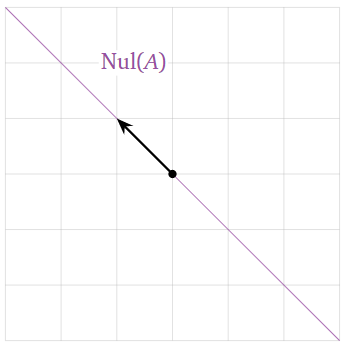
El espacio nulo es el conjunto de soluciones del sistema homogéneo\(Ax=0\). Para calcular esto, necesitamos remar reducir\(A\). Su forma de escalón de fila reducida es
\[\left(\begin{array}{cc}1&1\\0&0\\0&0\end{array}\right).\nonumber\]
Esto da la ecuación\(x+y=0\text{,}\) o
\[\left\{\begin{array}{rrr}x &=& -y\\ y &=& y\end{array}\right. \quad\xrightarrow{\text{parametric vector form}}\quad \left(\begin{array}{c}x\\y\end{array}\right)=y\left(\begin{array}{c}-1\\1\end{array}\right).\nonumber\]
De ahí que el espacio nulo sea el\(\text{Span}\bigl\{{-1\choose 1}\bigr\}\text{,}\) que es una línea en\(\mathbb{R}^2\).
Figura\(\PageIndex{11}\)
Observe que el espacio de columna es un subespacio de\(\mathbb{R}^3\text{,}\) mientras que el espacio nulo es un subespacio de\(\mathbb{R}^2\). Esto se debe a que\(A\) tiene tres filas y dos columnas.
El espacio de columna y el espacio nulo de una matriz son ambos subespacios, por lo que ambos son vanos. El espacio de columna de una matriz\(A\) se define como el lapso de las columnas de\(A\). El espacio nulo se define como el conjunto de soluciones de\(Ax=0\text{,}\) por lo que este es un buen ejemplo de una especie de subespacio que podemos definir sin ningún tipo de abarcamiento puesto en mente. En otras palabras, es más fácil demostrar que el espacio nulo es un subespacio que mostrar que es un tramo, ver la prueba anterior. Para hacer cálculos, sin embargo, suele ser necesario encontrar un conjunto de expansión.
El espacio nulo de una matriz es el conjunto de soluciones de un sistema homogéneo de ecuaciones. Por ejemplo, el espacio nulo de la matriz
\[A=\left(\begin{array}{ccc}1&7&2\\-2&1&3\\4&-2&-3\end{array}\right)\nonumber\]
es el conjunto de soluciones de\(Ax=0\text{,}\) i.e., el conjunto de soluciones del sistema de ecuaciones
\[\left\{\begin{array}{rrrrrrl} x &+& 7y &+& 2z &=& 0\\ -2x &+& y &+& 3z &=& 0\\ 4x &-& 2y &-& 3z &=& 0.\end{array}\right.\nonumber\]
Por el contrario, el conjunto de soluciones de cualquier sistema homogéneo de ecuaciones es precisamente el espacio nulo de la matriz de coeficientes correspondiente.
Para encontrar un conjunto de expansión para el espacio nulo, se tiene que resolver un sistema de ecuaciones homogéneas.
Para encontrar un conjunto de expansión para\(\text{Nul}(A)\text{,}\) calcular la forma vectorial paramétrica de las soluciones a la ecuación homogénea\(Ax=0\). Los vectores adjuntos a las variables libres forman un conjunto de expansión para\(\text{Nul}(A)\).
Encontrar un conjunto de expansión para el espacio nulo de la matriz
\[A=\left(\begin{array}{cccc}2&3&-8&-5 \\ -1&2&-3&-8\end{array}\right).\nonumber\]
Solución
Calculamos la forma vectorial paramétrica de las soluciones de\(Ax=0\). La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{cccc}1&0&-1&2 \\ 0&1&-2&-3\end{array}\right).\nonumber\]
Las variables libres son\(x_3\) y\(x_4\text{;}\) la forma paramétrica del conjunto de soluciones es
\[\left\{\begin{array}{rrrrr} x_1 &=& x_3 &-& 2x_4\\ x_2 &=& 2x_3 &+& 3x_4\\ x_3 &=& x_3&{}&{}\\ x_4 &=&{}&{}& x_4\end{array}\right. \quad\xrightarrow[\text{vector form}]{\text{parametric}}\quad \left(\begin{array}{c}x_1 \\x_2\\x_3\\x_4\end{array}\right)=x_3\left(\begin{array}{c}1\\2\\1\\0\end{array}\right)+x_4\left(\begin{array}{c}-2\\3\\0\\1\end{array}\right).\nonumber\]
Por lo tanto,
\[\text{Nul}(A)=\text{Span}\left\{\left(\begin{array}{c}1\\2\\1\\0\end{array}\right),\:\left(\begin{array}{c}-2\\3\\0\\1\end{array}\right)\right\}.\nonumber\]
Encontrar un conjunto de expansión para el espacio nulo de la matriz
\[A=\left(\begin{array}{cc}1&3\\2&4\end{array}\right).\nonumber\]
Solución
Calculamos la forma vectorial paramétrica de las soluciones de\(Ax=0\). La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{cc}1&0\\0&1\end{array}\right).\nonumber\]
No hay variables libres; de ahí que la única solución de\(Ax=0\) es la solución trivial. En otras palabras,
\[\text{Nul}(A)=\{0\}=\text{Span}\{0\}.\nonumber\]
Es natural definir para que\(\text{Span}\{\} = \{0\}\text{,}\) podamos tomar nuestro conjunto de expansión para estar vacío. Esto es congruente con la definición de dimensión, Definición 2.7.2, en la Sección 2.7.
Escribir un subespacio como un espacio de columna o un espacio nulo
Se te puede dar un subespacio de muchas formas diferentes. En la práctica, los cálculos que involucran subespacios son mucho más fáciles si tu subespacio es el espacio de columna o espacio nulo de una matriz. El ejemplo más simple de tal cálculo es encontrar un conjunto de expansión: un espacio de columna es por definición el tramo de las columnas de una matriz, y mostramos arriba cómo calcular un conjunto de expansión para un espacio nulo usando la forma vectorial paramétrica. Por ello, resulta útil reescribir un subespacio como un espacio de columna o un espacio nulo antes de intentar responder preguntas al respecto.
Al hacer preguntas sobre un subespacio, suele ser mejor reescribir el subespacio como un espacio de columna o un espacio nulo.
Esto también se aplica a la pregunta “¿mi subconjunto es un subespacio?” Si tu subconjunto es un espacio de columna o un espacio nulo de una matriz, entonces la respuesta es sí.
Let
\[V=\left\{\left(\begin{array}{c}a\\b\end{array}\right)\text{ in }\mathbb{R}^{2}|2a=3b\right\}\nonumber\]
ser el subconjunto de un Ejemplo anterior\(\PageIndex{9}\). El subconjunto\(V\) es exactamente el conjunto de soluciones de la ecuación homogénea\(2x - 3y = 0\). Por lo tanto,
\[V=\text{Nul} (2-3)\nonumber\]
En particular, se trata de un subespacio. La forma de escalón de fila reducida de\(\left(\begin{array}{cc}2&-3\end{array}\right)\) es\(\left(\begin{array}{cc}1&-3/2\end{array}\right)\), por lo que la forma paramétrica de\(V\) es\(x = 3/2y\text{,}\) así que la forma vectorial paramétrica es\({x\choose y} = y{3/2\choose 1},\) y, por lo tanto,\(\bigl\{{3/2\choose 1}\bigr\}\) abarca\(V\).
Dejado\(V\) ser el plano en\(\mathbb{R}^3\) definido por
\[V=\left\{\left(\begin{array}{c}2x+y \\ x-y \\ 3x-2y \end{array}\right) |x,y\text{ are in }\mathbb{R}\right\}.\nonumber\]
Escribir\(V\) como el espacio de columna de una matriz.
Solución
Desde
\[\left(\begin{array}{c}2x+y \\ x-y \\ 3x-2y\end{array}\right)=x\left(\begin{array}{c}2\\1\\3\end{array}\right)+y\left(\begin{array}{c}1\\-1\\-2\end{array}\right),\nonumber\]
notamos que\(V\) es exactamente el lapso de los vectores
\[\left(\begin{array}{c}2\\1\\3\end{array}\right)\quad\text{and}\quad\left(\begin{array}{c}1\\-1\\-2\end{array}\right).\nonumber\]
De ahí
\[V=\text{Col}\left(\begin{array}{cc}2&1\\1&-1\\3&-2\end{array}\right).\nonumber\]


