2.7: Base y Dimensión
- Page ID
- 113051
- Entender la definición de una base de un subespacio.
- Entender el teorema de base.
- Recetas: base para un espacio de columna, base para un espacio nulo, base de un lapso.
- Imagen: base de un subespacio de\(\mathbb{R}^2 \) o\(\mathbb{R}^3 \).
- Teorema: teorema de base.
- Palabras esenciales del vocabulario: base, dimensión.
Bases de un Subespacio
Como discutimos en la Sección 2.6, un subespacio es lo mismo que un lapso, excepto que no tenemos en mente un conjunto de vectores de expansión. Hay infinitamente muchas opciones de conjuntos de expansión para un subespacio distinto de cero; para evitar la redundancia, generalmente es más conveniente elegir un conjunto de expansión con el número mínimo de vectores en él. Esta es la idea detrás de la noción de una base.
Que\(V\) sea un subespacio de\(\mathbb{R}^n \). Una base de\(V\) es un conjunto de vectores de\(V\) tal\(\{v_1,v_2,\ldots,v_m\}\) manera que:
- \(V = \text{Span}\{v_1,v_2,\ldots,v_m\}\text{,}\)y
- el conjunto\(\{v_1,v_2,\ldots,v_m\}\) es linealmente independiente.
Recordemos que un conjunto de vectores es linealmente independiente si y solo si, cuando se elimina cualquier vector del conjunto, el span se contrae (Teorema 2.5.1 en la Sección 2.5). En otras palabras, si\(\{v_1,v_2,\ldots,v_m\}\) es una base de un subespacio,\(V\text{,}\) entonces ningún subconjunto apropiado de\(\{v_1,v_2,\ldots,v_m\}\) abarcará\(V\text{:}\), es un conjunto de expansión mínimo. Cualquier subespacio admite una base por el Teorema 2.6.1 en la Sección 2.6.
Un subespacio distinto de cero tiene infinitamente muchas bases diferentes, pero todas contienen el mismo número de vectores.
Lo dejamos como un ejercicio para demostrar que dos bases cualesquiera tienen el mismo número de vectores; uno podría querer esperar hasta después de aprender el teorema de la matriz invertible en la Sección 3.5.
Que\(V\) sea un subespacio de\(\mathbb{R}^n \). El número de vectores en cualquier base de\(V\) se llama la dimensión de\(V\text{,}\) y se escribe\(\dim V\).
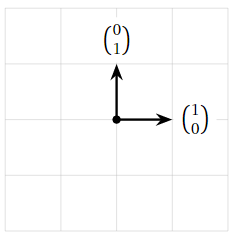
Encuentra una base de\(\mathbb{R}^2 \).
Solución
Necesitamos encontrar dos vectores en\(\mathbb{R}^2 \) ese lapso\(\mathbb{R}^2 \) y sean linealmente independientes. Una de esas bases es\(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\)
- Abarcan porque cualquier vector se\(a\choose b\) puede escribir como una combinación lineal de\({1\choose 0},{0\choose 1}\text{:}\)
\[\left(\begin{array}{c}a\\b\end{array}\right)=a\left(\begin{array}{c}1\\0\end{array}\right)+b\left(\begin{array}{c}0\\1\end{array}\right).\nonumber\] - Son linealmente independientes: si
\[x\left(\begin{array}{c}1\\0\end{array}\right)+y\left(\begin{array}{c}0\\1\end{array}\right)=\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}0\\0\end{array}\right)\nonumber\]
entonces\(x=y=0\).
Esto demuestra que el plano\(\mathbb{R}^2 \) tiene dimensión 2.
Figura\(\PageIndex{1}\)
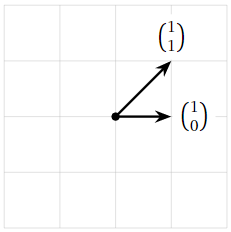
Encuentra todas las bases de\(\mathbb{R}^2 \).
Solución
Sabemos por el Ejemplo anterior\(\PageIndex{1}\) que\(\mathbb{R}^2 \) tiene dimensión 2, por lo que cualquier base de\(\mathbb{R}^2 \) tiene dos vectores en ella. Dejar\(v_1,v_2\) ser vectores adentro\(\mathbb{R}^2 \text{,}\) y dejar\(A\) ser la matriz con columnas\(v_1,v_2\).
- Decir que\(\{v_1,v_2\}\) abarca\(\mathbb{R}^2 \) significa que\(A\) tiene un pivote, Definición 1.2.5 en la Sección 1.2, en cada fila: ver Teorema 2.3.1 en la Sección 2.3.
- Decir que\(\{v_1,v_2\}\) es linealmente independiente significa que\(A\) tiene un pivote en cada columna: ver Receta: Comprobando independencia lineal en la Sección 2.5.
Ya que\(A\) es una\(2\times 2\) matriz, tiene un pivote en cada fila exactamente cuando tiene un pivote en cada columna. Por lo tanto, dos vectores no colineales forman una base de\(\mathbb{R}^2 \). Por ejemplo,
\[\left\{\left(\begin{array}{c}1\\0\end{array}\right),\:\left(\begin{array}{c}1\\1\end{array}\right)\right\}\nonumber\]
es una base.
Figura\(\PageIndex{2}\)
Uno muestra exactamente como en el ejemplo anterior\(\PageIndex{1}\) que los vectores de coordenadas estándar
\[e_1=\left(\begin{array}{c}1\\0\\ \vdots \\ 0\\0\end{array}\right),\quad e_2=\left(\begin{array}{c}0\\1\\ \vdots \\ 0\\0\end{array}\right),\quad\cdots ,\quad e_{n-1}=\left(\begin{array}{c}0\\0\\ \vdots \\1\\0\end{array}\right),\quad e_n=\left(\begin{array}{c}0\\0\\ \vdots \\0\\1\end{array}\right)\nonumber\]
formar una base para\(\mathbb{R}^n \). Esto a veces se conoce como la base estándar.
En particular,\(\mathbb{R}^n \) tiene dimensión\(n\).
El Ejemplo anterior\(\PageIndex{3}\) implica que cualquier base para\(\mathbb{R}^n \) tiene\(n\) vectores en él. Dejar\(v_1,v_2,\ldots,v_n\) ser vectores adentro\(\mathbb{R}^n \text{,}\) y dejar\(A\) ser la\(n\times n\) matriz con columnas\(v_1,v_2,\ldots,v_n\).
- Decir que\(\{v_1,v_2,\ldots,v_n\}\) vanos\(\mathbb{R}^n \) significa que\(A\) tiene una posición de pivote, Definición 1.2.5 en la Sección 1.2, en cada fila: ver este Teorema 2.3.1 en la Sección 2.3.
- Decir que\(\{v_1,v_2,\ldots,v_n\}\) es linealmente independiente significa que\(A\) tiene una posición de pivote en cada columna: ver Receta: Comprobando independencia lineal en la Sección 2.5.
Ya que\(A\) es una matriz cuadrada, tiene un pivote en cada fila si y solo si tiene un pivote en cada columna. Veremos en la Sección 3.5 que las dos condiciones anteriores son equivalentes a la invertibilidad de la matriz\(A\).
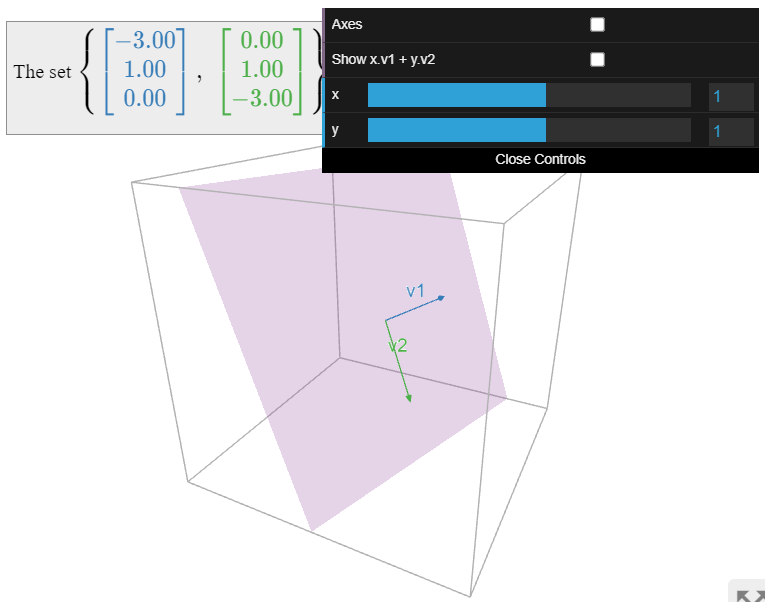
Let
\[V=\left\{\left(\begin{array}{c}x\\y\\z\end{array}\right)\text{ in }\mathbb{R}^{3}|x+3y+z=0\right\}\quad\mathcal{B}=\left\{\left(\begin{array}{c}-3\\1\\0\end{array}\right),\:\left(\begin{array}{c}0\\1\\-3\end{array}\right)\right\}.\nonumber\]
Verificar que\(V\) es un subespacio, y mostrar directamente que\(\mathcal{B}\) es una base para\(V\).
Solución
Primero observamos que\(V\) es el conjunto de soluciones de la ecuación homogénea\(x + 3y + z = 0\text{,}\) por lo que es un subespacio: ver esta nota en la Sección 2.6, Nota 2.6.3. Para demostrar que\(\mathcal{B}\) es una base, realmente necesitamos verificar tres cosas:
- Ambos vectores están en\(V\) porque
\[\begin{array}{rrrrrrl} (-3) &+& 3(1) &+& (0) &=& 0\\ (0) &+& 3(1) &+& (-3) &=& 0.\end{array}\nonumber\] - Span: supongamos que\(\left(\begin{array}{c}x\\y\\z\end{array}\right)\) está en\(V\). Ya que\(x + 3y + z = 0\) tenemos\(y = -\frac 13(x+z)\text{,}\) así\(\mathcal{B}\) vanos de
\[\left(\begin{array}{c}x\\y\\z\end{array}\right)=\left(\begin{array}{c}x\\ {-\frac{1}{3}(x+z)} \\ z\end{array}\right)=-\frac{x}{3}\left(\begin{array}{c}-3\\1\\0\end{array}\right)-\frac{z}{3}\left(\begin{array}{c}0\\1\\-3\end{array}\right).\nonumber\]
ahí\(V\). - Linealmente independiente:
\[c_1\left(\begin{array}{c}-3\\1\\0\end{array}\right)+c_2\left(\begin{array}{c}0\\1\\-3\end{array}\right)=0\implies\left(\begin{array}{c}-3c_1 \\ c_1+c_2 \\ -3c_2\end{array}\right)=\left(\begin{array}{c}0\\0\\0\end{array}\right)\implies c_1=c_2=0.\nonumber\]
Alternativamente, se puede observar que los dos vectores no son colineales.
Ya que\(V\) tiene una base con dos vectores, tiene dimensión dos: es un plano.
Este ejemplo es algo ideado, en el sentido de que aprenderemos métodos sistemáticos para verificar que un subconjunto es una base. La intención es ilustrar las propiedades definitorias de una base.
Computar una base para un subespacio
Ahora mostramos cómo encontrar bases para el espacio de columna de una matriz y el espacio nulo de una matriz. Para encontrar una base para un subespacio dado, suele ser mejor reescribir primero el subespacio como un espacio de columna o un espacio nulo: vea esta nota en la Sección 2.6, Nota 2.6.3
Una base para el espacio de columna
Primero mostramos cómo calcular una base para el espacio de columna de una matriz.
Las columnas pivotes de una matriz\(A\) forman una base para\(\text{Col}(A)\).
- Prueba
-
Esta es una reafirmación del Teorema 2.5.3 en la Sección 2.5.
El teorema anterior se refiere a las columnas pivotes en la matriz original, no a su forma de escalón de fila reducida. De hecho, una matriz y su forma de escalón de fila reducida generalmente tienen diferentes espacios de columna. Por ejemplo, en la matriz\(A\) a continuación:
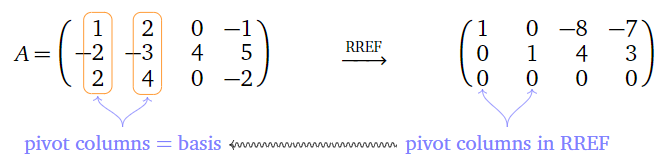
Figura\(\PageIndex{4}\)
las columnas pivotes son las dos primeras columnas, por lo que una base para\(\text{Col}(A)\) es
\[\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right)\right\}.\nonumber\]
Las dos primeras columnas de la forma escalón de fila reducida ciertamente abarcan un subespacio diferente, como
\[\text{Span}\left\{\left(\begin{array}{c}1\\0\\0\end{array}\right),\:\left(\begin{array}{c}0\\1\\0\end{array}\right)\right\}=\left\{\left(\begin{array}{c}a\\b\\0\end{array}\right)|a,b\text{ in }\mathbb{R}\right\}=(x,y\text{-plane}),\nonumber\]
pero\(\text{Col}(A)\) contiene vectores cuya última coordenada es distinta de cero.
La dimensión de\(\text{Col}(A)\) es el número de pivotes de\(A\).
Una base de un lapso
Computar una base para un lapso es lo mismo que calcular una base para un espacio de columna. De hecho, el lapso de muchos vectores finitamente\(v_1,v_2,\ldots,v_m\) es el espacio de columna de una matriz, es decir, la matriz\(A\) cuyas columnas son\(v_1,v_2,\ldots,v_m\text{:}\)
\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots &v_m \\ |&|&\quad &|\end{array}\right).\nonumber\]
Encontrar una base del subespacio
\[V=\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right),\:\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}.\nonumber\]
Solución
El subespacio\(V\) es el espacio de columna de la matriz
\[A=\left(\begin{array}{cccc}1&2&0&-1 \\ -2&-3&4&5 \\ 2&4&0&-2\end{array}\right).\nonumber\]
La forma de escalón de fila reducida de esta matriz es
\[\left(\begin{array}{cccc}1&0&-8&-7 \\ 0&1&4&3 \\ 0&0&0&0\end{array}\right).\nonumber\]
Las dos primeras columnas son columnas pivotes, por lo que una base para\(V\) es
\[\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right)\right\}.\nonumber\]
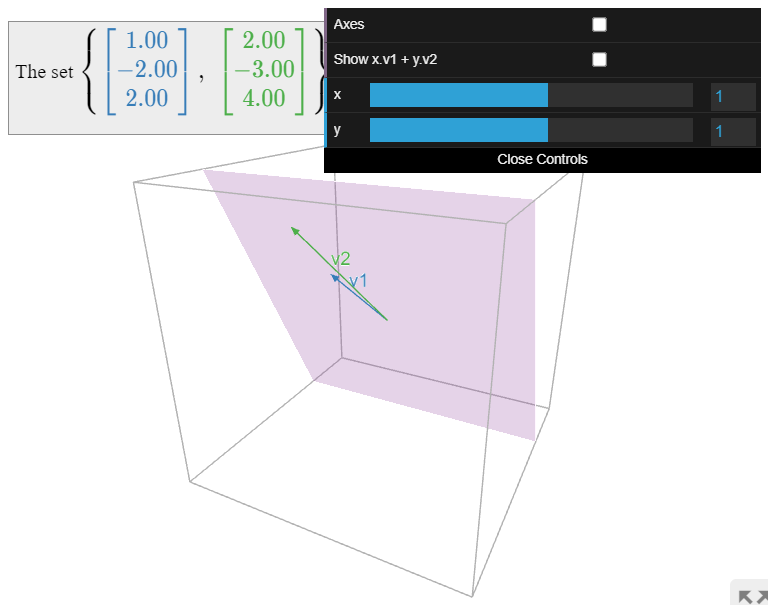
Encontrar una base del subespacio
\[V=\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right),\:\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}\nonumber\]
que no consiste en los dos primeros vectores, como en el Ejemplo anterior\(\PageIndex{6}\).
Solución
El punto de este ejemplo es que el Teorema anterior\(\PageIndex{1}\) da una base para que\(V\text{;}\) como siempre, hay infinitamente más.
Reordenando los vectores, podemos expresar\(V\) como el espacio de columna de
\[A'=\left(\begin{array}{cccc}0&-1&1&2 \\ 4&5&-2&-3 \\ 0&-2&2&4\end{array}\right).\nonumber\]
La forma de escalón de fila reducida de esta matriz es
\[\left(\begin{array}{cccc}1&0&3/4 &7/4 \\ 0&1&-1&-2 \\ 0&0&0&0\end{array}\right).\nonumber\]
Las dos primeras columnas son columnas pivotes, por lo que una base para\(V\) es
\[\left\{\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}.\nonumber\]
Estos son los dos últimos vectores en el conjunto de expansión dado.
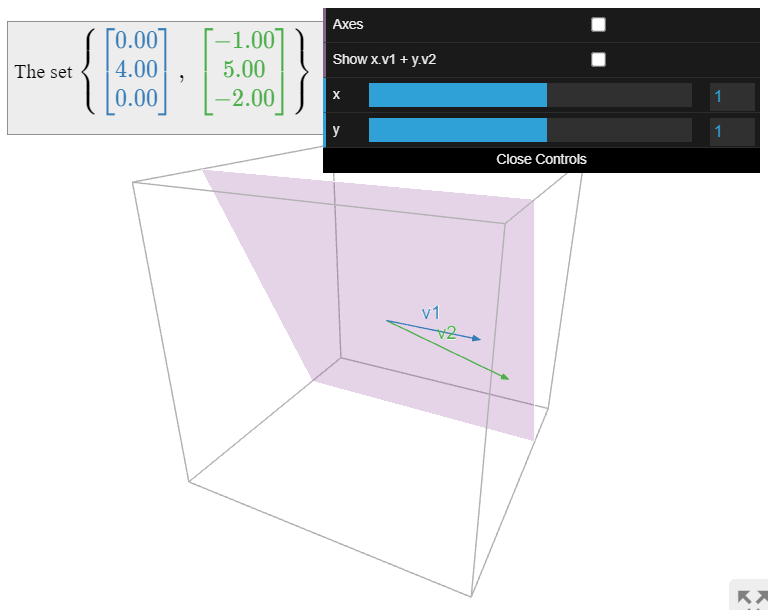
Una base para el espacio nulo
Para calcular una base para el espacio nulo de una matriz, se tiene que encontrar la forma vectorial paramétrica de las soluciones de la ecuación homogénea\(Ax=0\).
Los vectores unidos a las variables libres en la forma de vector paramétrico del conjunto de solución\(Ax=0\) forman una base de\(\text{Nul}(A)\).
La prueba del teorema tiene dos partes. La primera parte es que cada solución se encuentra en el lapso de los vectores dados. Esto es automático: los vectores se eligen exactamente para que cada solución sea una combinación lineal de esos vectores. La segunda parte es que los vectores son linealmente independientes. Esta parte se discutió en el Ejemplo 2.5.3 en la Sección 2.5.
Una base para un subespacio general
Como se mencionó al inicio de esta subsección, cuando se le da un subespacio escrito en una forma diferente, para calcular una base suele ser mejor reescribirla como un espacio de columna o espacio nulo de una matriz.
\(V\)Sea el subespacio definido por
\[V=\left\{\left(\begin{array}{c}x\\y\\z\end{array}\right)|x+2y=z\right\}.\nonumber\]
Encuentra una base para\(V\). Qué es\(\dim(V)\text{?}\)
Solución
Primero notamos que\(V\) es exactamente el conjunto de soluciones de la ecuación lineal homogénea\(x + 2y - z = 0\). Por lo tanto,\(V = \text{Nul}\left(\begin{array}{ccc}1&2&-1\end{array}\right).\) esta matriz está en forma de escalón de fila reducida; la forma paramétrica de la solución general es\(x = -2y + z\text{,}\) así que la forma vectorial paramétrica es
\[\left(\begin{array}{c}x\\y\\z\end{array}\right)=y\left(\begin{array}{c}-2\\1\\0\end{array}\right)=z\left(\begin{array}{c}1\\0\\1\end{array}\right).\nonumber\]
De ello se deduce que una base es
\[\left\{\left(\begin{array}{c}-2\\1\\0\end{array}\right),\:\left(\begin{array}{c}1\\0\\1\end{array}\right)\right\}.\nonumber\]
Ya que\(V\) tiene una base con dos vectores, su dimensión\(2\text{:}\) es que es un plano.
El teorema de la base
Recordemos que\(\{v_1,v_2,\ldots,v_n\}\) forma una base para\(\mathbb{R}^n \) si y sólo si la matriz\(A\) con columnas\(v_1,v_2,\ldots,v_n\) tiene un pivote en cada fila y columna (ver este Ejemplo\(\PageIndex{4}\)). Dado que\(A\) es una\(n\times n\) matriz, estas dos condiciones son equivalentes: los vectores abarcan si y sólo si son linealmente independientes. El teorema de base es una versión abstracta de la afirmación anterior, que se aplica a cualquier subespacio.
\(V\)Sea un subespacio de dimensión\(m\). Entonces:
- Cualquier vector\(m\) linealmente independiente en\(V\) forma de base para\(V\).
- Cualquier\(m\) vector que se extiende\(V\) forma una base para\(V\).
- Prueba
-
Supongamos que\(\mathcal{B} = \{v_1,v_2,\ldots,v_m\}\) es un conjunto de vectores linealmente independientes en\(V\). Para demostrar que\(\mathcal{B}\) es una base para\(V\text{,}\) debemos probar que\(V = \text{Span}\{v_1,v_2,\ldots,v_m\}.\) Si no, entonces existe algún vector\(v_{m+1}\) en\(V\) que no está contenido en\(\text{Span}\{v_1,v_2,\ldots,v_m\}.\) Por el criterio de lapso creciente Teorema 2.5.2 en la Sección 2.5, el conjunto también\(\{v_1,v_2,\ldots,v_m,v_{m+1}\}\) es linealmente independiente. Continuando de esta manera, seguimos eligiendo vectores hasta que finalmente tenemos un conjunto de expansión linealmente independiente: digamos\(V = \text{Span}\{v_1,v_2,\ldots,v_m,\ldots,v_{m+k}\}\). Entonces\(\{v_1,v_2,\ldots,v_{m+k}\}\) es una base para\(V\text{,}\) lo cual implica eso\(\dim(V) = m+k > m\). Pero estábamos asumiendo que\(V\) tiene dimensión\(m\text{,}\) así que ya\(\mathcal{B}\) debió haber sido una base.
Ahora supongamos que eso\(\mathcal{B} = \{v_1,v_2,\ldots,v_m\}\) abarca\(V\). Si no\(\mathcal{B}\) es linealmente independiente, entonces por este Teorema 2.5.1 en la Sección 2.5, podemos eliminar algún número de vectores\(\mathcal{B}\) sin reducir su lapso. Después de reordenar, podemos suponer que eliminamos los últimos\(k\) vectores sin reducir el span, y que no podemos eliminar más. Ahora\(V = \text{Span}\{v_1,v_2,\ldots,v_{m-k}\}\text{,}\) y\(\{v_1,v_2,\ldots,v_{m-k}\}\) es una base para\(V\) porque es linealmente independiente. Esto implica que\(\dim V=m-k < m\). Pero estábamos asumiendo que\(\dim V = m\text{,}\) así\(\mathcal{B}\) debió haber sido ya una base.
Es decir, si ya lo sabes\(\dim V = m\text{,}\) y si tienes un conjunto de\(m\) vectores\(\mathcal{B} = \{v_1,v_2,\ldots,v_m\}\) en\(V\text{,}\) entonces solo tienes que marcar uno de:
- \(\mathcal{B}\)es linealmente independiente, o
- \(\mathcal{B}\)abarca\(V\text{,}\)
para\(\mathcal{B}\) que sea una base de\(V\). Si aún no lo sabías\(\dim V = m\text{,}\) entonces tendrías que revisar ambas propiedades.
Para decirlo de otra manera, supongamos que tenemos un conjunto de vectores\(\mathcal{B} = \{v_1,v_2,\ldots,v_m\}\) en un subespacio\(V\). Entonces, si alguna de las siguientes afirmaciones es cierta, la tercera también debe ser cierta:
- \(\mathcal{B}\)es linealmente independiente,
- \(\mathcal{B}\)abarca\(V\text{,}\) y
- \(\dim V = m.\)
Por ejemplo, si\(V\) es un plano, entonces dos vectores no colineales cualesquiera\(V\) forman una base.
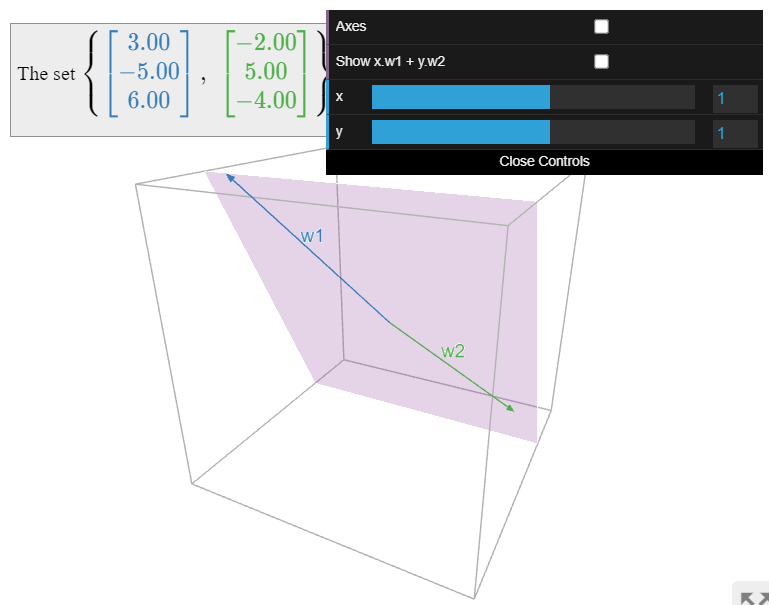
Encontrar una base del subespacio
\[V=\text{Span}\left\{\left(\begin{array}{c}1\\-2\\2\end{array}\right),\:\left(\begin{array}{c}2\\-3\\4\end{array}\right),\:\left(\begin{array}{c}0\\4\\0\end{array}\right),\:\left(\begin{array}{c}-1\\5\\-2\end{array}\right)\right\}\nonumber\]
que es diferente de las bases en este Ejemplo\(\PageIndex{6}\) y en este Ejemplo\(\PageIndex{7}\).
Solución
Sabemos por los ejemplos anteriores que\(\dim V = 2\). Por el Teorema\(\PageIndex{3}\), basta con encontrar dos vectores no colineales cualesquiera en\(V\). Escribimos dos combinaciones lineales de los cuatro vectores de expansión dados, elegidos al azar:
\[w_1=\left(\begin{array}{c}1\\-2\\2\end{array}\right)+\left(\begin{array}{c}2\\-3\\4\end{array}\right)=\left(\begin{array}{c}3\\-5\\6\end{array}\right)\quad w_2=-\left(\begin{array}{c}2\\-3\\4\end{array}\right)+\frac{1}{2}\left(\begin{array}{c}0\\4\\0\end{array}\right)=\left(\begin{array}{c}-2\\5\\-4\end{array}\right).\nonumber\]
Ya que no\(w_1,w_2\) son colineales,\(\mathcal{B} = \{w_1,w_2\}\) es una base para\(V\).
Encuentra una base para el avión
\[V=\left\{\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)|x_1 +x_2=x_3\right\}\nonumber\]
por inspección. (Este plano se expresa en notación de constructor de conjuntos, Nota 2.2.3 en la Sección 2.2.)
Solución
Primero tenga en cuenta que\(V\) es el espacio nulo de la matriz\(\left(\begin{array}{ccc}1&1&-1\end{array}\right)\) esta matriz está en forma de escalón de fila reducida y tiene dos variables libres, por lo que\(V\) es de hecho un plano. Escribimos dos vectores satisfactorios\(x_1 + x_2 = x_3\text{:}\)
\[v_1=\left(\begin{array}{c}1\\0\\1\end{array}\right)\quad v_2=\left(\begin{array}{c}0\\1\\1\end{array}\right).\nonumber\]
Dado que\(v_1\) y no\(v_2\) son colineales, son linealmente independientes; ya que\(\dim(V) = 2\text{,}\) el teorema de base implica que\(\{v_1,v_2\}\) es una base para\(V\).


