3.2: Uno a uno y sobre transformaciones
- Page ID
- 113088
- Comprender las definiciones de uno a uno y sobre transformaciones.
- Recetas: verificar si una transformación matricial es uno a uno y/o sobre.
- Imágenes: ejemplos de transformaciones matriciales que son/no son uno a uno y/o sobre.
- Palabras de vocabulario: uno-a-uno, onto.
En esta sección, discutimos dos de las preguntas más básicas que uno puede hacer sobre una transformación: si es uno a uno y/o sobre. Para una transformación matricial, traducimos estas preguntas al lenguaje de las matrices.
Transformaciones uno a uno
Una transformación\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) es uno a uno si, por cada vector\(b\) en\(\mathbb{R}^m \text{,}\) la ecuación\(T(x)=b\) tiene como máximo una solución\(x\) en\(\mathbb{R}^n \).
Otra palabra para uno a uno es inyectivo.
Aquí hay algunas formas equivalentes de decir que\(T\) es uno a uno:
- Por cada vector\(b\) en\(\mathbb{R}^m \text{,}\) la ecuación\(T(x) = b\) tiene cero o una solución\(x\) en\(\mathbb{R}^n \).
- Diferentes entradas de\(T\) tienen diferentes salidas.
- Si\(T(u) = T(v)\) entonces\(u=v\).
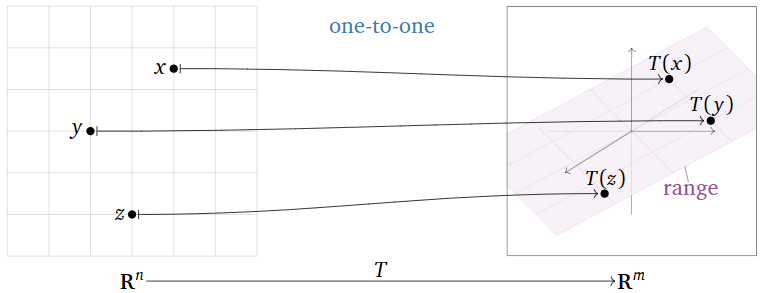
Figura\(\PageIndex{1}\)
Aquí hay algunas formas equivalentes de decir que no\(T\) es uno a uno:
- Existe algún vector\(b\) en\(\mathbb{R}^m \) tal que la ecuación\(T(x)=b\) tiene más de una solución\(x\) en\(\mathbb{R}^n \).
- Hay dos entradas diferentes de\(T\) con la misma salida.
- Existen vectores\(u,v\) tales que\(u\neq v\) pero\(T(u)=T(v)\).
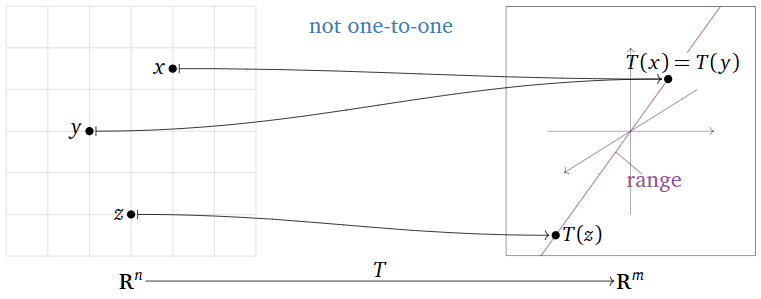
Figura\(\PageIndex{2}\)
La función no\(\sin\colon \mathbb{R} \to\mathbb{R} \) es uno a uno. En efecto,\(\sin(0) = \sin(\pi) = 0\text{,}\) por lo que las entradas\(0\) y\(\pi\) tienen la misma salida\(0\). De hecho, la ecuación\(\sin(x) = 0\) tiene infinitamente muchas soluciones\(\ldots,-2\pi,-\pi,0,\pi,2\pi,\ldots\).
La función\(\exp\colon \mathbb{R} \to\mathbb{R} \) definida por\(\exp(x) = e^x\) es uno a uno. En efecto, si\(T(x) = T(y)\text{,}\) entonces es\(e^x = e^y\text{,}\) así\(\ln(e^x) = \ln(e^y)\text{,}\) y por lo tanto\(x = y\). La ecuación\(T(x) = C\) tiene una solución\(x = \ln(C)\) si\(C > 0\text{,}\) y tiene cero soluciones si\(C\leq 0\).
La función\(f\colon \mathbb{R} \to\mathbb{R} \) definida por\(f(x)=x^3\) es uno a uno. En efecto, si\(f(x) = f(y)\) entonces\(x^3 = y^3\text{;}\) tomar raíces cubitas da\(x = y\). En otras palabras, la única solución de\(f(x) = C\) es\(x=\sqrt[3]C\).
La función\(f\colon \mathbb{R} \to\mathbb{R} \) definida por no\(f(x)=x^3-x\) es uno a uno. En efecto,\(f(0) = f(1) = f(-1) = 0\text{,}\) por lo que\(0,1,-1\) todas las entradas tienen la misma salida\(0\). Las soluciones de la ecuación\(x^3 - x = 0\) son exactamente las raíces de\(f(x) = x(x-1)(x+1)\text{,}\) y esta ecuación tiene tres raíces.
La función\(f\colon \mathbb{R} \to\mathbb{R} \) definida por no\(f(x)=x^2\) es uno a uno. En efecto,\(f(1) = 1 = f(-1)\text{,}\) por lo que las entradas\(1\) y\(-1\) tienen las mismas salidas. La función\(g\colon \mathbb{R} \to\mathbb{R} \) definida por no\(g(x)=|x|\) es uno-a-uno por la misma razón.
Supongamos que está construyendo un brazo de robot con tres articulaciones que pueden mover su mano alrededor de un plano, como en el Ejemplo 3.1.11 en la Sección 3.1.
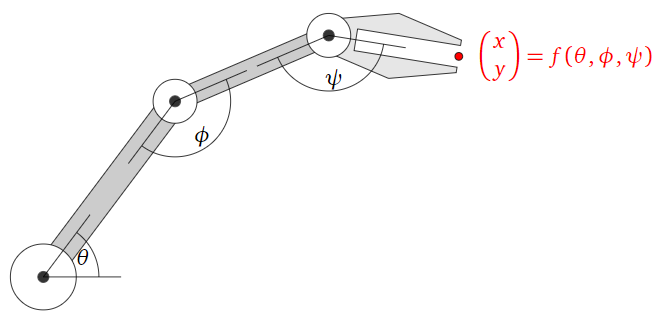
Figura\(\PageIndex{3}\)
Definir una transformación de la\(f\colon\mathbb{R}^3 \to\mathbb{R}^2 \) siguiente manera:\(f(\theta,\phi,\psi)\) es la\((x,y)\) posición de la mano cuando las juntas se rotan en ángulos\(\theta, \phi, \psi\text{,}\) respectivamente. Preguntar si\(f\) es uno a uno es lo mismo que preguntar si hay más de una forma de mover el brazo para llegar a tu taza de café. (Hay.)
Dejar\(A\) ser una\(m\times n\) matriz, y dejar\(T(x)=Ax\) ser la transformación matricial asociada. Las siguientes declaraciones son equivalentes:
- \(T\)es uno a uno.
- Para cada uno\(b\) en\(\mathbb{R}^m \text{,}\) la ecuación\(T(x)=b\) tiene como máximo una solución.
- Para cada uno\(b\) en\(\mathbb{R}^m \text{,}\) la ecuación\(Ax=b\) tiene una solución única o es inconsistente.
- \(Ax=0\)tiene sólo la solución trivial.
- Las columnas de\(A\) son linealmente independientes.
- \(A\)tiene un pivote en cada columna.
- El rango de\(T\) tiene dimensión\(n\).
- Prueba
-
Los estados 1, 2 y 3 son traducciones entre sí. La equivalencia de 3 y 4 se desprende de la observación clave 2.4.3 en la Sección 2.4: si\(Ax=0\) tiene una sola solución, entonces\(Ax=b\) tiene una sola solución también, o es inconsistente. La equivalencia de 4, 5 y 6 es consecuencia de la Receta: Comprobación de la Independencia Lineal en la Sección 2.5, y la equivalencia de 6 y 7 se deriva del hecho de que el rango de una matriz es igual al número de columnas con pivotes.
Recordemos que equivalente significa que, para una matriz dada, o todas las declaraciones son verdaderas simultáneamente, o todas son falsas.
Deja que\(A\) sea la matriz
\[A=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) por\(T(x) = Ax\). ¿Es\(T\) uno a uno?
Solución
La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right).\nonumber\]
De ahí\(A\) que tenga un pivote en cada columna, así\(T\) es uno a uno.
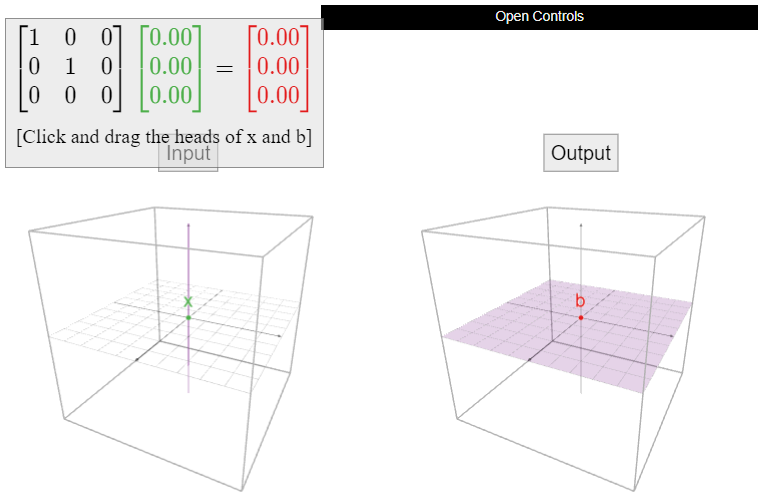
Let
\[A=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \) por\(T(x) = Ax\). ¿Es\(T\) uno a uno? Si no, encuentra dos vectores diferentes de\(u,v\) tal manera que\(T(u)=T(v)\).
Solución
La matriz ya\(A\) está en forma de escalón de fila reducida. No tiene pivote en cada columna, por lo que no\(T\) es uno a uno. Por lo tanto, sabemos por el Teorema\(\PageIndex{1}\) que\(Ax=0\) tiene soluciones no triviales. Si\(v\) es una solución no trivial (es decir, distinta de cero) de\(Av = 0\text{,}\) entonces\(T(v) = Av = 0 = A0 = T(0)\text{,}\) así\(0\) y\(v\) son vectores diferentes con la misma salida. Por ejemplo,
\[T\left(\begin{array}{c}0\\0\\1\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right)\:\left(\begin{array}{c}0\\0\\1\end{array}\right)=0=T\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]
Geométricamente,\(T\) es proyección sobre el\(xy\) plano. Dos vectores cualesquiera que se encuentren en la misma línea vertical tendrán la misma proyección. Porque\(b\) en el\(xy\) plano -el conjunto de soluciones de\(T(x) = b\) es toda la línea vertical que contiene\(b\). En particular,\(T(x) = b\) tiene infinitamente muchas soluciones.
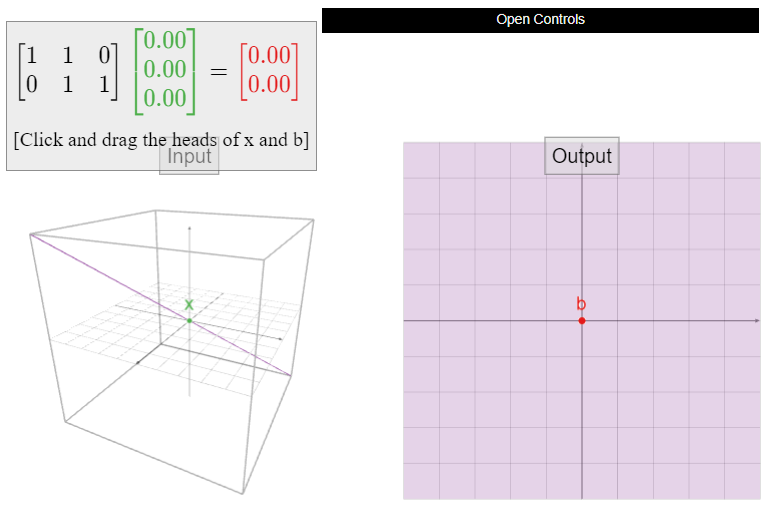
Deja que\(A\) sea la matriz
\[A=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) por\(T(x) = Ax\). ¿Es\(T\) uno a uno? Si no, encuentra dos vectores diferentes de\(u,v\) tal manera que\(T(u)=T(v)\).
Solución
La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{ccc}1&0&-1\\0&1&1\end{array}\right).\nonumber\]
No hay un pivote en cada columna, así que no\(T\) es uno a uno. Por lo tanto, sabemos por Teorema\(\PageIndex{1}\) que\(Ax=0\) tiene soluciones no triviales. Si\(v\) es una solución no trivial (es decir, distinta de cero) de\(Av = 0\text{,}\) entonces\(T(v) = Av = 0 = A0 = T(0)\text{,}\) así\(0\) y\(v\) son vectores diferentes con la misma salida. Para encontrar una solución no trivial, encontramos la forma paramétrica de las soluciones de\(Ax=0\) usar la matriz reducida anterior:
\[\left\{\begin{array}{rrrrrrr}x &{}&{}& -& z &=& 0\\ {}&{}& y& + &z &=& 0\end{array}\right.\quad\implies\quad\left\{\begin{array}{rrr}x&=&z \\ y&=&-z\end{array}\right.\nonumber\]
La variable libre es\(z\). Tomar\(z=1\) da la solución no trivial
\[T\left(\begin{array}{c}1\\-1\\1\end{array}\right)=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)\:\left(\begin{array}{c}1\\-1\\1\end{array}\right)=0=T\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]
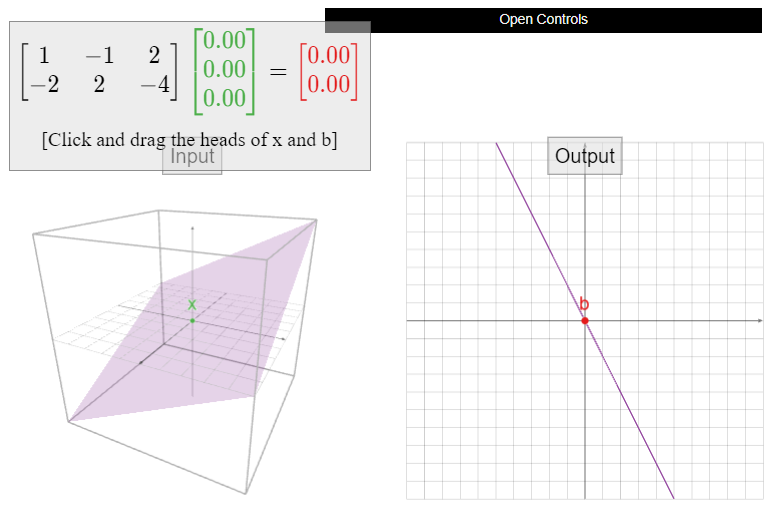
Let
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) por\(T(x) = Ax\). ¿Es\(T\) uno a uno? Si no, encuentra dos vectores diferentes de\(u,v\) tal manera que\(T(u)=T(v)\).
Solución
La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{ccc}1&-1&2\\0&0&0\end{array}\right).\nonumber\]
No hay un pivote en cada columna, así que no\(T\) es uno a uno. Por lo tanto, sabemos por Teorema\(\PageIndex{1}\) que\(Ax=0\) tiene soluciones no triviales. Si\(v\) es una solución no trivial (es decir, distinta de cero) de\(Av = 0\text{,}\) entonces\(T(v) = Av = 0 = A0 = T(0)\text{,}\) así\(0\) y\(v\) son vectores diferentes con la misma salida. Para encontrar una solución no trivial, encontramos la forma paramétrica de las soluciones de\(Ax=0\) usar la matriz reducida anterior:
\[ x - y + 2z = 0 \quad\implies\quad x = y - 2z. \nonumber \]
Las variables libres son\(y\) y\(z\). Tomando\(y=1\) y\(z=0\) da la solución no trivial
\[T\left(\begin{array}{c}1\\1\\0\end{array}\right)=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right)\:\left(\begin{array}{c}1\\1\\0\end{array}\right)=0=T\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]
Los tres ejemplos anteriores se pueden resumir de la siguiente manera. Supongamos que\(T(x)=Ax\) es una transformación matricial que no es uno-a-uno. Por teorema\(\PageIndex{1}\), hay una solución no trivial de\(Ax=0\). Esto significa que el espacio nulo de no\(A\) es el espacio cero. Todos los vectores en el espacio nulo son soluciones a\(T(x)=0\). Si calcula un vector distinto de cero\(v\) en el espacio nulo (reduciendo filas y encontrando la forma paramétrica del conjunto de soluciones de,\(Ax=0\text{,}\) por ejemplo), entonces\(v\) y\(0\) ambos tienen la misma salida:\(T(v) = Av = 0 = T(0).\)
Si\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) es una transformación de matriz uno a uno, ¿qué podemos decir sobre los tamaños relativos de\(n\) y\(m\text{?}\)
La matriz asociada a\(T\) tiene\(n\) columnas y\(m\) filas. Cada fila y cada columna solo pueden contener un pivote, por lo que\(A\) para tener un pivote en cada columna, debe tener al menos tantas filas como columnas:\(n\leq m\).
Esto dice que, por ejemplo,\(\mathbb{R}^3 \) es “demasiado grande” para admitir una transformación lineal uno a uno en\(\mathbb{R}^2 \).
Tenga en cuenta que existen matrices altas que no son uno a uno: por ejemplo,
\[\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\\0&0&0\end{array}\right)\nonumber\]
no tiene un pivote en cada columna.
Sobre Transformaciones
Una transformación\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) es sobre si, por cada vector\(b\) en\(\mathbb{R}^m \text{,}\) la ecuación\(T(x)=b\) tiene al menos una solución\(x\) en\(\mathbb{R}^n \).
Otra palabra para onto es suryectiva.
Aquí hay algunas formas equivalentes de decir que\(T\) está en:
- El rango de\(T\) es igual al codominio de\(T\).
- Cada vector en el codominio es la salida de algún vector de entrada.
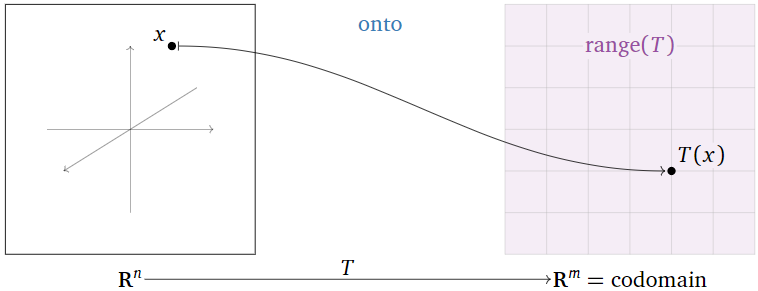
Figura\(\PageIndex{8}\)
Aquí hay algunas formas equivalentes de decir que no\(T\) está en:
- El rango de\(T\) es menor que el codominio de\(T\).
- Existe un vector\(b\) en\(\mathbb{R}^m \) tal que la ecuación\(T(x)=b\) no tiene solución.
- Hay un vector en el codominio que no es la salida de ningún vector de entrada.
Figura\(\PageIndex{9}\)
La función no\(\sin\colon \mathbb{R} \to\mathbb{R} \) está en. En efecto, tomar\(b=2\text{,}\) la ecuación no\(\sin(x)=2\) tiene solución. El rango de\(\sin\) es el intervalo cerrado\([-1,1]\text{,}\) que es menor que el codominio\(\mathbb{R}\).
La función\(\exp\colon \mathbb{R} \to\mathbb{R} \) definida por no\(\exp(x) = e^x\) es on. En efecto, tomar\(b=-1\text{,}\) la ecuación no\(\exp(x) = e^x = -1\) tiene solución. El rango de\(\exp\) es el conjunto\((0,\infty)\) de todos los números reales positivos.
La función\(f\colon \mathbb{R} \to\mathbb{R} \) definida por\(f(x)=x^3\) es onto. En efecto, la ecuación\(f(x) = x^3 = b\) siempre tiene la solución\(x = \sqrt[3]b\).
La función\(f\colon \mathbb{R} \to\mathbb{R} \) definida por\(f(x)=x^3-x\) es onto. En efecto, las soluciones de la ecuación\(f(x) = x^3 - x = b\) son las raíces del polinomio\(x^3 - x - b\text{;}\) ya que este es un polinomio cúbico, tiene al menos una raíz real.
La transformación del brazo robot del Ejemplo no\(\PageIndex{2}\) está en. El robot no puede alcanzar objetos que están muy lejos.
Dejar\(A\) ser una\(m\times n\) matriz, y dejar\(T(x)=Ax\) ser la transformación matricial asociada. Las siguientes declaraciones son equivalentes:
- \(T\)está en.
- \(T(x)=b\)tiene al menos una solución para cada\(b\) entrada\(\mathbb{R}^m \).
- \(Ax=b\)es consistente para cada uno\(b\) en\(\mathbb{R}^m \).
- Las columnas de\(A\) span\(\mathbb{R}^m \).
- \(A\)tiene un pivote en cada fila.
- El rango de\(T\) tiene dimensión\(m\).
- Prueba
-
Los estados 1, 2 y 3 son traducciones entre sí. La equivalencia de 3, 4, 5 y 6 se desprende del Teorema 2.3.1 en la Sección 2.3.
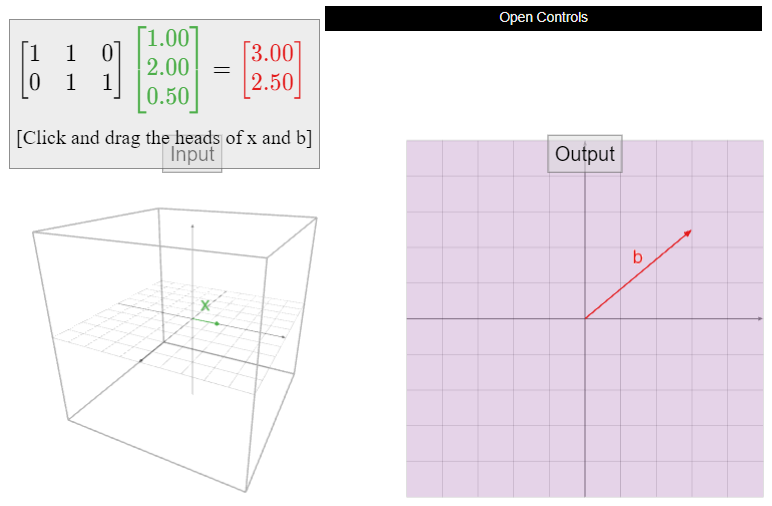
Deja que\(A\) sea la matriz
\[A=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) por\(T(x) = Ax\). ¿Está\(T\) onto?
Solución
La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{ccc}1&0&-1\\0&1&1\end{array}\right).\nonumber\]
De ahí\(A\) que tenga un pivote en cada fila, así\(T\) es sobre.
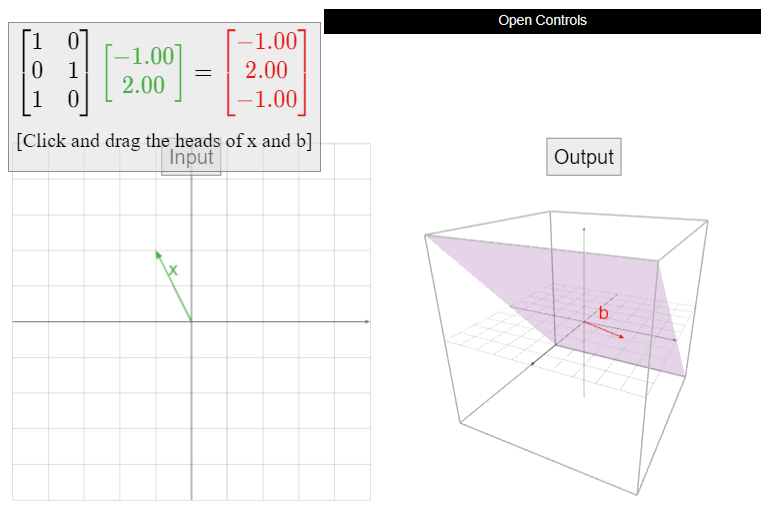
Deja que\(A\) sea la matriz
\[A=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) por\(T(x) = Ax\). ¿Está\(T\) onto? Si no, encuentra un vector\(b\) en\(\mathbb{R}^3 \) tal que no\(T(x)=b\) tenga solución.
Solución
La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right).\nonumber\]
De ahí que\(A\) no tenga un pivote en cada fila, así que no\(T\) está encendido. De hecho, ya que
\[T\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right)\:\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}x\\y\\x\end{array}\right),\nonumber\]
vemos que por cada vector de salida de\(T\text{,}\) la tercera entrada es igual a la primera. Por lo tanto,
\[ b=(1,2,3) \nonumber \]
no está en el rango de\(T\).
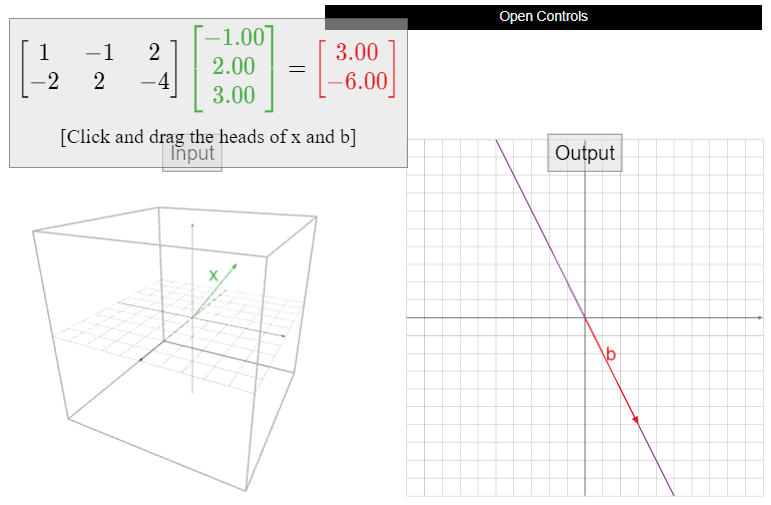
Let
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&4\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) por\(T(x) = Ax\). ¿Está\(T\) onto? Si no, encuentra un vector\(b\) en\(\mathbb{R}^2 \) tal que no\(T(x)=b\) tenga solución.
Solución
La forma de escalón de fila reducida de\(A\) es
\[\left(\begin{array}{ccc}1&-1&2\\0&0&0\end{array}\right).\nonumber\]
No hay un pivote en cada fila, así que no\(T\) está encendido. El rango de\(T\) es\(A\text{,}\) cuyo espacio de columna es igual a
\[\text{Span}\left\{\left(\begin{array}{c}1\\-2\end{array}\right),\:\left(\begin{array}{c}-1\\2\end{array}\right),\:\left(\begin{array}{c}2\\-4\end{array}\right)\right\}=\text{Span}\left\{\left(\begin{array}{c}1\\-2\end{array}\right)\right\},\nonumber\]
ya que las tres columnas de\(A\) son colineales. Por lo tanto, cualquier vector que no esté en la línea a través no\(1\choose-2\) está en el rango de\(T\). Por ejemplo, si\(b={1\choose 1}\) entonces no\(T(x)=b\) tiene solución.
Los dos ejemplos anteriores ilustran la siguiente observación. Supongamos que\(T(x)=Ax\) es una transformación matricial que no está en. Esto quiere decir que\(\text{range}(T) = \text{Col}(A)\) es un subespacio\(\mathbb{R}^m \) de dimensión menor que\(m\text{:}\) quizás sea una línea en el plano, o una línea en el\(3\) espacio, o un plano en el\(3\) espacio, etc. Sea cual sea el caso, el rango de\(T\) es muy pequeño en comparación con el codominio. Para encontrar un vector que no esté en el rango de\(T\text{,}\) elegir un vector aleatorio distinto de cero\(b\) en\(\mathbb{R}^m \text{;}\) tienes que ser extremadamente desafortunado para elegir un vector que esté en el rango de\(T\). Por supuesto, para comprobar si un vector dado\(b\) está en el rango de hay\(T\text{,}\) que resolver la ecuación matricial\(Ax=b\) para ver si es consistente.
Si\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) es una transformación en matriz, ¿qué podemos decir sobre los tamaños relativos de\(n\) y\(m\text{?}\)
La matriz asociada a\(T\) tiene\(n\) columnas y\(m\) filas. Cada fila y cada columna solo pueden contener un pivote, por lo que\(A\) para tener un pivote en cada fila, debe tener al menos tantas columnas como filas:\(m\leq n\).
Esto dice que, por ejemplo,\(\mathbb{R}^2 \) es “demasiado pequeño” para admitir una transformación lineal a\(\mathbb{R}^3 \).
Tenga en cuenta que existen matrices anchas que no están en: por ejemplo,
\[\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right)\nonumber\]
no tiene un pivote en cada fila.
Comparativa
Las exposiciones anteriores de uno a uno y sobre transformaciones fueron escritas para reflejarse entre sí. Sin embargo, “uno a uno” y “onto” son nociones complementarias: ninguna implica la otra. A continuación hemos proporcionado un gráfico para comparar los dos. En el gráfico,\(A\) es una\(m\times n\) matriz, y\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) es la transformación matricial\(T(x)=Ax\).
Mesa\(\PageIndex{1}\)
| \(T\)es uno a uno | \(T\)está en |
|---|---|
| \ (T\) es uno-a-uno">\(T(x)=b\) tiene como máximo una solución para cada\(b\). | \ (T\) es onto">\(T(x)=b\) tiene al menos una solución para cada\(b\). |
| \ (T\) es uno a uno">Las columnas de\(A\) son linealmente independientes. | \ (T\) está ento">Las columnas de\(A\) span\(\mathbb{R}^m\). |
| \ (T\) es uno a uno">\(A\) tiene una columna pivote en cada columna. | \ (T\) está en">\(A\) tiene un pivote en cada fila. |
| \ (T\) es uno a uno">El rango de\(T\) tiene dimensión\(n\). | \ (T\) está ento">El rango de\(T\) tiene dimensión\(m\). |
La función no\(\sin\colon \mathbb{R} \to\mathbb{R} \) es ni uno a uno ni on.
La función\(\exp\colon \mathbb{R} \to\mathbb{R} \) definida por\(\exp(x) = e^x\) es uno a uno pero no on.
La función\(f\colon \mathbb{R} \to\mathbb{R} \) definida por\(f(x)=x^3\) es uno a uno y on.
La función\(f\colon \mathbb{R} \to\mathbb{R} \) definida por\(f(x)=x^3-x\) es on pero no uno-a-uno.
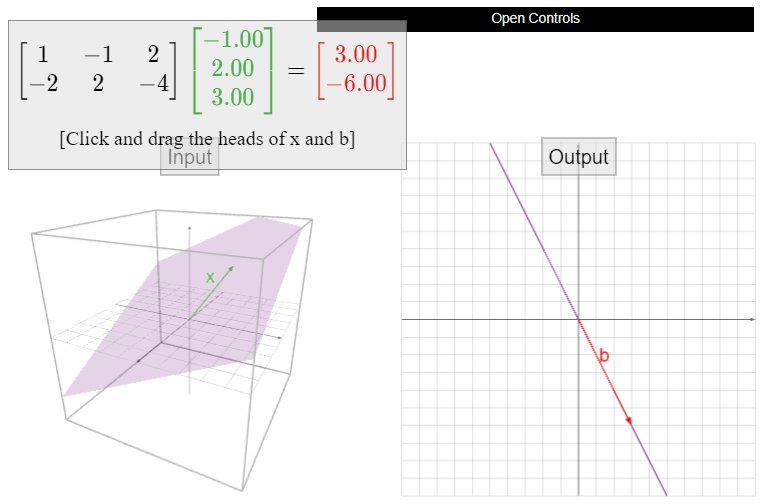
Let
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) por\(T(x) = Ax\). Esta transformación no es ni uno a uno ni sobre, como vimos en Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{11}\).
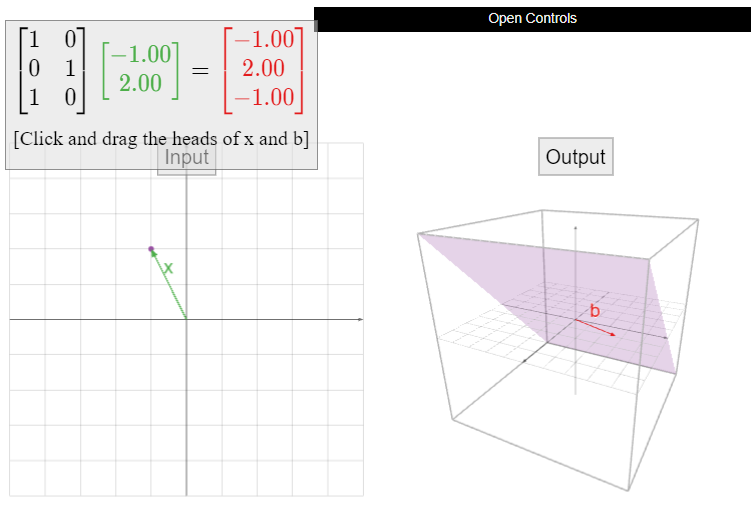
Deja que\(A\) sea la matriz
\[A=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) por\(T(x) = Ax\). Esta transformación es uno-a-uno pero no sobre, como vimos en este Ejemplo\(\PageIndex{3}\) y en este Ejemplo\(\PageIndex{10}\).
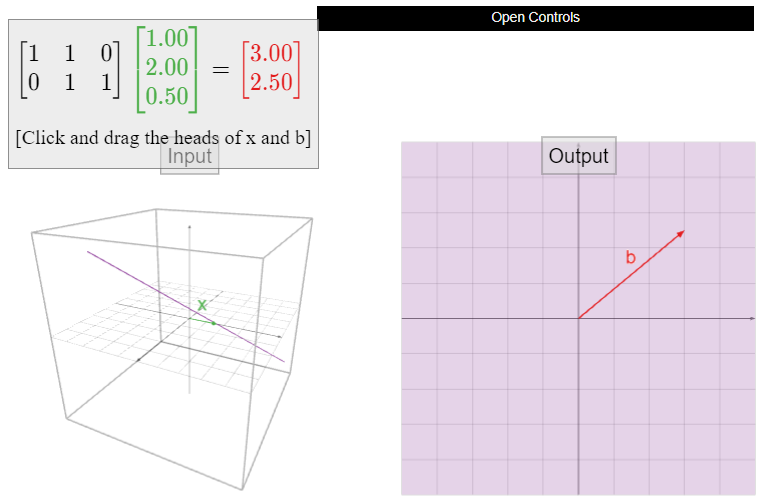
Deja que\(A\) sea la matriz
\[A=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right),\nonumber\]
y definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) por\(T(x) = Ax\). Esta transformación es sobre pero no uno a uno, como vimos en Ejemplo\(\PageIndex{9}\).
En la Subsección Matrices como Funciones en la Sección 3.1, discutimos las transformaciones definidas por varias\(2\times 2\) matrices, a saber:
\ begin {align*}\ text {Reflection:} &\ qquad A=\ left (\ begin {array} {cc} -1&0\\ 0&1\ end {array}\ right)\\\ text {Dilatación:} &\ qquad A=\ left (\ begin {array} {cc} 1.5&0\\ 0&1.5\ end {array}\ right)\\ text {Identidad:} &\ qquad A=\ left (\ begin {array} {cc} 1&0\\ 0&1\ end {array}\ derecha)\\\ text {Rotación:} &\ qquad A=\ left (\ begin {array} {cc} 0&-1\\ 1&0\ end {array}\ right)\\\ text {Shear:} &\ qquad A=\ left (\ begin {array} {cc} 1&1\\ 0&1\ end {array}\ right). \ end {alinear*}
En cada caso, la transformación matricial asociada\(T(x)=Ax\) es tanto uno a uno como a uno. Una\(2\times 2\) matriz\(A\) tiene un pivote en cada fila si y solo si tiene un pivote en cada columna (si y solo si tiene dos pivotes), así que en este caso, la transformación\(T\) es uno a uno si y solo si está en. Se puede ver geométricamente que están en (¿cuál es la entrada para una salida dada?) , o que son uno a uno usando el hecho de que las columnas de no\(A\) son colineales.

Observamos en el Ejemplo anterior\(\PageIndex{16}\) que una matriz cuadrada tiene un pivote en cada fila si y solo si tiene un pivote en cada columna. Por lo tanto, una transformación matricial\(T\) de\(\mathbb{R}^n \) a sí misma es uno-a-uno si y sólo si está en: en este caso, las dos nociones son equivalentes.
Por el contrario, por Nota\(\PageIndex{1}\) y Nota\(\PageIndex{2}\), si una transformación de matriz\(T\colon\mathbb{R}^m \to\mathbb{R}^n \) es tanto uno a uno como hacia, entonces\(m=n\).
Tenga en cuenta que en general, una transformación\(T\) es tanto uno a uno como a si y solo si\(T(x)=b\) tiene exactamente una solución para todos\(b\) en\(\mathbb{R}^m \).


