3.3: Transformaciones lineales
- Page ID
- 113089
- Aprende a verificar que una transformación es lineal, o probar que una transformación no es lineal.
- Comprender la relación entre transformaciones lineales y transformaciones matriciales.
- Receta: computar la matriz de una transformación lineal.
- Teorema: transformaciones lineales y transformaciones matriciales.
- Notación: los vectores de coordenadas estándar\(e_1,e_2,\ldots\).
- Palabras de vocabulario: transformación lineal, matriz estándar, matriz de identidad.
En la Sección 3.1, estudiamos la geometría de las matrices considerándolas como funciones, es decir, considerando las transformaciones matriciales asociadas. Definimos cierto vocabulario (dominio, codominio, rango) y formulamos una serie de preguntas naturales sobre una transformación. Para una transformación matricial, estas se traducen en preguntas sobre matrices, que tenemos muchas herramientas para responder.
En esta sección, hacemos un cambio de perspectiva. Supongamos que se nos da una transformación que nos gustaría estudiar. Si podemos probar que nuestra transformación es una transformación matricial, entonces podemos usar álgebra lineal para estudiarla. Esto plantea dos preguntas importantes:
- ¿Cómo podemos saber si una transformación es una transformación matricial?
- Si nuestra transformación es una transformación matricial, ¿cómo encontramos su matriz?
Por ejemplo, vimos en el Ejemplo 3.1.7 en la Sección 3.1 que la transformación matricial
\[ T\colon\mathbb{R}^2\to \mathbb{R}^2 \qquad T(x) = \left(\begin{array}{cc}0&-1\\1&0\end{array}\right)x \nonumber \]
es una rotación en sentido contrario a las agujas del reloj del plano por\(90^\circ\). Sin embargo, podríamos haber definido\(T\) de esta manera:
\[ T\colon\mathbb{R}^2\to \mathbb{R}^2 \qquad T(x) = \text{the counterclockwise rotation of $x$ by $90^\circ$}. \nonumber \]
Dada esta definición, no es en absoluto obvio que\(T\) es una transformación matricial, o a qué matriz está asociada.
Transformaciones Lineales: Definición
En esta sección, presentamos la clase de transformaciones que provienen de matrices.
Una transformación lineal es una transformación\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) satisfactoria
\ comenzar {alinear*} T (u + v) &= T (u) + T (v)\\ T (cu) &= cT (u)\ final {alinear*}
para todos los vectores\(u,v\) en\(\mathbb{R}^n \) y todos los escalares\(c\).
Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) ser una transformación matricial:\(T(x)=Ax\) para una\(m\times n\) matriz\(A\). Por la Proposición 2.3.1 en la Sección 2.3, tenemos
\ begin {alinear*} T (u + v) &= A (u + v) &= Au + Av = T (u) + T (v)\\ T (cu) &= A (cu) &= CaU = cT (u)\ final {alinear*}
para todos los vectores\(u,v\) en\(\mathbb{R}^n \) y todos los escalares\(c\). Dado que una transformación matricial satisface las dos propiedades definitorias, es una transformación lineal
Veremos en la siguiente Subsección La Matriz de una Transformación Lineal que lo contrario es cierto: cada transformación lineal es una transformación matricial; simplemente aún no hemos calculado su matriz.
Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) ser una transformación lineal. Entonces:
- \(T(0)=0\).
- Para cualquier vector\(v_1,v_2,\ldots,v_k\) en\(\mathbb{R}^n \) y escalar\(c_1,c_2,\ldots,c_k\text{,}\) tenemos
\[T(c_1v_1+c_2v_2+\cdots +c_kv_k)=c_1T(v_1)+c_2T(v_2)+\cdots +c_kT(v_k).\nonumber\]
- Prueba
-
- Ya que\(0 = -0\text{,}\) tenemos
\[ T(0) = T(-0) = -T(0) \nonumber \]
por la segunda propiedad definitoria, Definición\(\PageIndex{1}\). El único vector\(w\) tal que\(w=-w\) es el vector cero. - Supongamos que por simplicidad eso\(k=2\). Entonces
\ begin {align*} T (c_1v_1 + c_2v_2) &= T (c_1v_1) + T (c_2v_2) &\ text {primera propiedad}\\ &= C_1t (v_1) + C_2t (v_2) &\ text {segunda propiedad.} \ end {alinear*}
- Ya que\(0 = -0\text{,}\) tenemos
En ingeniería, el segundo hecho se llama principio de superposición; debería recordarle la propiedad distributiva. Por ejemplo,\(T(cu + dv) = cT(u) + dT(v)\) para cualquier vector\(u,v\) y cualquier escalar\(c,d\). Para replantear el primer hecho:
Una transformación lineal necesariamente lleva el vector cero al vector cero.
Definir\(T\colon \mathbb{R} \to \mathbb{R}\) por\(T(x) = x+1\). ¿Es\(T\) una transformación lineal?
Solución
Nosotros tenemos\(T(0) = 0 + 1 = 1\). Dado que cualquier transformación lineal necesariamente toma de cero a cero por la nota importante anterior\(\PageIndex{1}\), concluimos que no\(T\) es lineal (aunque su gráfica sea una línea).
Nota: en este caso, no fue necesario verificar explícitamente que\(T\) no satisfaga ambas propiedades definitorias, Definición\(\PageIndex{1}\): ya que\(T(0)=0\) es consecuencia de estas propiedades, al menos una de ellas no debe ser satisfecha. (De hecho, esto no\(T\) satisface a ninguno.)
Definir\(T\colon\mathbb{R}^2\to\mathbb{R}^2\) por\(T(x)=1.5x\). Verificar que\(T\) sea lineal.
Solución
Tenemos que verificar las propiedades definitorias, Definición\(\PageIndex{1}\), para todos los vectores\(u,v\) y todos los escalares\(c\). En otras palabras, tenemos que tratar\(u,v,\) y\(c\) como incógnitas. Lo único que se nos permite usar es la definición de\(T\).
\ begin {alinear*} T (u + v) &= 1.5 (u + v) = 1.5u + 1.5v = T (u) + T (v)\\ T (cu) &= 1.5 (cu) = c (1.5u) = cT (u). \ end {alinear*}
Ya que\(T\) satisface tanto las propiedades definitorias,\(T\) es lineal.
Nota: sabemos por el Ejemplo 3.1.5 en la Sección 3.1 que\(T\) es una transformación matricial: de hecho,
\[ T(x) = \left(\begin{array}{cc}1.5&0\\0&1.5\end{array}\right) x. \nonumber \]
Dado que una transformación matricial es una transformación lineal, esta es otra prueba que\(T\) es lineal.
Definir\(T\colon\mathbb{R}^2\to\mathbb{R}^2\) por
\[ T(x) = \text{ the vector $x$ rotated counterclockwise by the angle $\theta$}. \nonumber \]
Verificar que\(T\) sea lineal.
Solución
Ya que\(T\) se define geométricamente, damos un argumento geométrico. Para la primera propiedad,\(T(u) + T(v)\) es la suma de los vectores obtenidos por rotación\(u\) y\(v\) por\(\theta\). Al otro lado de la ecuación,\(T(u+v)\) se encuentra el vector obtenido rotando la suma de los vectores\(u\) y\(v\). Pero no importa si sumamos o rotamos primero, como muestra el siguiente cuadro.
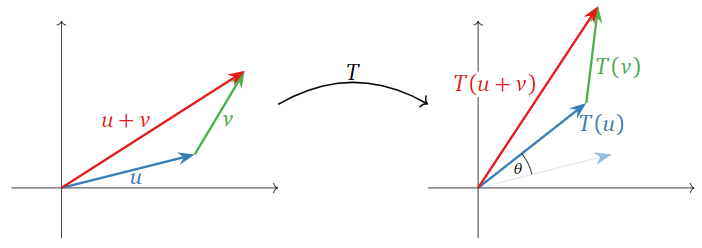
Figura\(\PageIndex{1}\)
Para la segunda propiedad,\(cT(u)\) es el vector obtenido rotando\(u\) por el ángulo\(\theta\text{,}\) luego cambiando su longitud por un factor de\(c\) (invertir dirección de\(c<0\). Por otro lado,\(T(cu)\) primero cambia la longitud de\(c\text{,}\) luego gira. Pero no importa en qué orden hagamos estas dos operaciones.
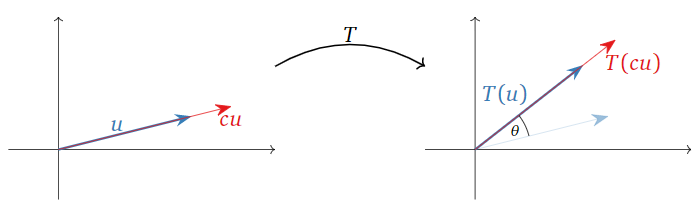
Figura\(\PageIndex{2}\)
Esto verifica que\(T\) sea una transformación lineal. Encontraremos su matriz en la siguiente Subsección La Matriz de una Transformación Lineal. Obsérvese sin embargo que no es nada obvio que se\(T\) pueda expresar como multiplicación por una matriz.
Definir\(T\colon\mathbb{R}^2\to\mathbb{R}^3 \) por la fórmula
\[T\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}3x-y\\y\\x\end{array}\right).\nonumber\]
Verificar que\(T\) sea lineal.
Solución
Tenemos que verificar las propiedades definitorias, Definición\(\PageIndex{1}\), para todos los vectores\(u,v\) y todos los escalares\(c\). Es decir, tenemos que tratar\(u,v,\) y\(c\) como incógnitas; lo único que se nos permite usar es la definición de\(T\). Ya que\(T\) se define en términos de las coordenadas de\(u,v\text{,}\) necesitamos dar esos nombres también; digamos\(u={x_1\choose y_1}\) y\(v={x_2\choose y_2}\). Para la primera propiedad, tenemos
\[\begin{aligned} T\left(\left(\begin{array}{c}x_1\\y_1\end{array}\right)+\left(\begin{array}{c}x_2\\y_2\end{array}\right)\right)&=T\left(\begin{array}{c}x_1+x_2\\y_1+y_2\end{array}\right)=\left(\begin{array}{c}3(x_1+x_2)-(y_1+y_2) \\ y_1+y_2 \\ x_1+x_2\end{array}\right) \\ &=\left(\begin{array}{c} (3x_1-y_1)+(3x_2-y_2) \\ y_1+y_2 \\ x_1+x_2\end{array}\right) \\ &=\left(\begin{array}{c}3x_1-y_1 \\ y_1 \\ x_1\end{array}\right)+\left(\begin{array}{c}3x_2-y_2 \\ y_2\\x_2\end{array}\right)=T\left(\begin{array}{c}x_1\\y_1\end{array}\right)+T\left(\begin{array}{c}x_2\\y_2\end{array}\right).\end{aligned}\nonumber\]
Para el segundo inmueble,
\[\begin{aligned}T\left(c\left(\begin{array}{c}x_1\\y_1\end{array}\right)\right)&=T\left(\begin{array}{c}cx_1\\cy_1\end{array}\right)=\left(\begin{array}{c}3(cx_1)-(cy_1) \\ cy_1 \\ cx_1\end{array}\right) \\ &=\left(\begin{array}{c}c(3x_1-y_1)\\cy_1\\cx_1\end{array}\right)=c\left(\begin{array}{c}3x_1-y_1\\y_1\\x_1\end{array}\right)=cT\left(\begin{array}{c}x_1\\y_1\end{array}\right).\end{aligned}\]
Dado que\(T\) satisface las propiedades definitorias, Definición\(\PageIndex{1}\),\(T\) es una transformación lineal.
Nota: veremos en este Ejemplo\(\PageIndex{9}\) a continuación que
\[T\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}3&-1\\0&1\\1&0\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right).\nonumber\]
De ahí\(T\) que, de hecho, sea una transformación matricial.
Se puede mostrar que, si una transformación es definida por fórmulas en las coordenadas como en el ejemplo anterior, entonces la transformación es lineal si y sólo si cada coordenada es una expresión lineal en las variables sin término constante.
Definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \) por
\[ T(x) = x + \left(\begin{array}{c}1\\2\\3\end{array}\right). \nonumber \]
Este tipo de transformación se llama traducción. Al igual que en un Ejemplo anterior\(\PageIndex{1}\), este no\(T\) es lineal, porque no\(T(0)\) es el vector cero.
Verifique que las siguientes transformaciones de\(\mathbb{R}^2\) a no\(\mathbb{R}^2\) sean lineales:
\[T_1\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}|x|\\y\end{array}\right)\quad T_2\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}xy\\y\end{array}\right)\quad T_3\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}2x+1\\x-2y\end{array}\right).\nonumber\]
Solución
Para verificar que una transformación no\(T\) es lineal, tenemos que demostrar que\(T\) no satisface al menos una de las dos propiedades definitorias, Definición\(\PageIndex{1}\). Para el primero, la negación de la declaración “\(T(u+v)=T(u)+T(v)\)para todos los vectores\(u,v\)” es “existe al menos un par de vectores\(u,v\) tal que”\(T(u+v)\neq T(u)+T(v)\). Es decir, basta con encontrar un ejemplo de un par de vectores\(u,v\) tal que\(T(u+v)\neq T(u)+T(v)\). De igual manera, para el segundo, la negación de la sentencia “\(T(cu) = cT(u)\)para todos los vectores\(u\) y todos los escalares\(c\)” es “existe algún vector\(u\) y algún escalar\(c\) tal que”\(T(cu)\neq cT(u)\). En otras palabras, basta con encontrar un vector\(u\) y un escalar\(c\) tal que\(T(cu)\neq cT(u)\).
Para la primera transformación, observamos que
\[T_1\left(-\left(\begin{array}{c}1\\0\end{array}\right)\right)=T_1\left(\begin{array}{c}-1\\0\end{array}\right)=\left(\begin{array}{c}|-1|\\0\end{array}\right)=\left(\begin{array}{c}1\\0\end{array}\right)\nonumber\]
pero que
\[-T_1\left(\begin{array}{c}1\\0\end{array}\right)=-\left(\begin{array}{c}|1|\\0\end{array}\right)=-\left(\begin{array}{c}1\\0\end{array}\right)=\left(\begin{array}{c}-1\\0\end{array}\right).\nonumber\]
Por lo tanto, esta transformación no satisface la segunda propiedad.
Para la segunda transformación, observamos que
\[T_2\left(2\left(\begin{array}{c}1\\1\end{array}\right)\right)=T_2\left(\begin{array}{c}2\\2\end{array}\right)=\left(\begin{array}{c}2\cdot 2\\2\end{array}\right)=\left(\begin{array}{c}4\\2\end{array}\right)\nonumber\]
pero que
\[2T_2\left(\begin{array}{c}1\\1\end{array}\right)=2\left(\begin{array}{c}1\cdot 1\\1\end{array}\right)=2\left(\begin{array}{c}1\\1\end{array}\right)=\left(\begin{array}{c}2\\2\end{array}\right).\nonumber\]
Por lo tanto, esta transformación no satisface la segunda propiedad.
Para la tercera transformación, observamos que
\[T_3\left(\begin{array}{c}0\\0\end{array}\right)=\left(\begin{array}{c}2(0)+1\\0-2(0)\end{array}\right)=\left(\begin{array}{c}1\\0\end{array}\right)\neq\left(\begin{array}{c}0\\0\end{array}\right).\nonumber\]
Dado que\(T_3\) no toma el vector cero al vector cero, no puede ser lineal.
A la hora de decidir si una transformación\(T\) es lineal, generalmente lo primero que se debe hacer es verificar\(T(0)=0\text{;}\) si no,\(T\) es automáticamente no lineal. Sin embargo, tenga en cuenta que las transformaciones no lineales\(T_1\) y\(T_2\) del ejemplo anterior toman el vector cero al vector cero.
Encuentra un ejemplo de una transformación que satisfaga la primera propiedad de linealidad, Definición\(\PageIndex{1}\), pero no la segunda.
Los vectores de coordenadas estándar
En la siguiente subsección, presentaremos la relación entre transformaciones lineales y transformaciones matriciales. Antes de hacerlo, necesitamos la siguiente notación importante.
Los vectores de coordenadas estándar en\(\mathbb{R}^n \) son los\(n\) vectores
\[e_1=\left(\begin{array}{c}1\\0\\ \vdots\\0\\0\end{array}\right),\quad e_2=\left(\begin{array}{c}0\\1\\ \vdots\\0\\0\end{array}\right),\quad\cdots ,\quad e_{n-1}=\left(\begin{array}{c}0\\0\\ \vdots\\1\\0\end{array}\right),\quad e_n=\left(\begin{array}{c}0\\0\\ \vdots\\0\\1\end{array}\right).\nonumber\]
La entrada\(i\) th de\(e_i\) es igual a 1, y las otras entradas son cero.
A partir de ahora, para el resto del libro, utilizaremos los símbolos\(\color{red}e_1,e_2,\ldots\) para denotar los vectores de coordenadas estándar.
Hay una ambigüedad en esta notación: hay que saber por contexto que\(e_1\) se pretende tener\(n\) entradas. Es decir, los vectores
\[\left(\begin{array}{c}1\\0\end{array}\right)\quad\text{and}\quad\left(\begin{array}{c}1\\0\\0\end{array}\right)\nonumber\]
ambos pueden ser denotados\(e_1\text{,}\) dependiendo de si estamos discutiendo vectores en\(\mathbb{R}^2\) o en\(\mathbb{R}^3 \).
Los vectores de coordenadas estándar en\(\mathbb{R}^2\) y\(\mathbb{R}^3 \) se muestran a continuación.
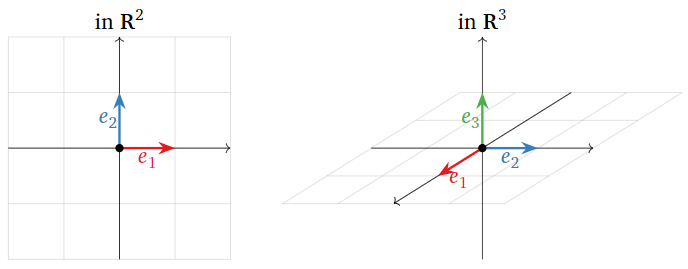
Figura\(\PageIndex{3}\)
Estos son los vectores de longitud 1 que apuntan en las direcciones positivas de cada uno de los ejes.
Si\(A\) es una\(m\times n\) matriz con columnas\(v_1,v_2,\ldots,v_m\text{,}\) entonces\(\color{red}Ae_i = v_i\) para cada\(i=1,2,\ldots,n\text{:}\)
\[\left(\begin{array}{cccc}|&|&\quad &| \\ v_1&v_2&\quad &v_n \\ |&|&\quad &|\end{array}\right)e_i=v_i.\nonumber\]
En otras palabras, multiplicar una matriz por\(e_i\) simplemente selecciona su\(i\) ésima columna.
Por ejemplo,
\[\left(\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right)\:\left(\begin{array}{c}1\\0\\0\end{array}\right)=\left(\begin{array}{c}1\\4\\7\end{array}\right)\quad\left(\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right)\:\left(\begin{array}{c}0\\1\\0\end{array}\right)=\left(\begin{array}{c}2\\5\\8\end{array}\right)\quad\left(\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right)\:\left(\begin{array}{c}0\\0\\01\end{array}\right)=\left(\begin{array}{c}3\\6\\9\end{array}\right).\nonumber\]
La matriz de\(n\times n\) identidad es la matriz\(I_n\) cuyas columnas son los vectores de coordenadas\(n\) estándar en\(\mathbb{R}^n \text{:}\)
\[I_n=\left(\begin{array}{ccccc}1&0&\cdots &0&0 \\ 0&1&\cdots &0&0 \\ \vdots &\vdots &\ddots &\vdots &\vdots \\ 0&0&\cdots &1&0 \\ 0&0&\cdots &0&1\end{array}\right).\nonumber\]
Veremos en este Ejemplo\(\PageIndex{10}\) a continuación que la matriz de identidad es la matriz de la transformación de identidad, Definición 3.1.2.
La Matriz de una Transformación Lineal
Ahora podemos probar que cada transformación lineal es una transformación matricial, y mostraremos cómo calcular la matriz.
Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) ser una transformación lineal. Deja\(A\) ser la\(m\times n\) matriz
\[A=\left(\begin{array}{cccc}|&|&\quad&| \\ T(e_1)&T(e_2)&\cdots&T(e_n) \\ |&|&\quad&|\end{array}\right).\nonumber\]
Entonces\(T\) es la transformación matricial asociada a\(A\text{:}\) eso es,\(T(x) = Ax\).
- Prueba
-
Suponemos por simplicidad que\(T\) es una transformación de\(\mathbb{R}^3 \) a\(\mathbb{R}^2\). Dejar\(A\) ser la matriz dada en el enunciado del teorema. Entonces
\[\begin{aligned}T\left(\begin{array}{c}x\\y\\z\end{array}\right);&=T\left(x\left(\begin{array}{c}1\\0\\0\end{array}\right)+y\left(\begin{array}{c}0\\1\\0\end{array}\right)+z\left(\begin{array}{c}0\\0\\1\end{array}\right)\right) \\ &=T(xe_1+ye_2+ze_3) \\ &=xT(e_1)+yT(e_2)+zT(e_3) \\ &=\left(\begin{array}{ccc}|&|&| \\ T(e_1)&T(e_2)&T(e_3) \\ |&|&|\end{array}\right)\:\left(\begin{array}{c}x\\y\\z\end{array}\right) \\ &=A\left(\begin{array}{c}x\\y\\z\end{array}\right).\end{aligned}\nonumber\]
La matriz\(A\) en el teorema anterior se llama la matriz estándar para\(T\). Las columnas de\(A\) son los vectores obtenidos evaluando\(T\) sobre los vectores de coordenadas\(n\) estándar en\(\mathbb{R}^n \). Para resumir parte del teorema:
Las transformaciones matriciales son las mismas que las transformaciones lineales.
Las transformaciones lineales son las mismas que las transformaciones matriciales, que provienen de matrices. La correspondencia se puede resumir en el siguiente diccionario.
\[\begin{aligned} \begin{array}{c}T:\mathbb{R}^n\to\mathbb{R}^m \\ {\text{Linear transformation}}\end{array}\quad &\longrightarrow m\times n\text{ matrix }A=\left(\begin{array}{cccc}|&|&\quad&| \\ T(e_1)&T(e_2)&\cdots &T(e_n) \\ |&|&\quad&|\end{array}\right) \\ \begin{array}{c}T:\mathbb{R}^n\to\mathbb{R}^m \\ T(x)=Ax\end{array} \quad &\longleftarrow m\times n\text{ matrix }A\end{aligned}\]
Definir\(T\colon\mathbb{R}^2\to\mathbb{R}^2\) por\(T(x)=1.5x\). Encuentre la matriz estándar\(A\) para\(T\).
Solución
Las columnas de\(A\) se obtienen evaluando\(T\) sobre los vectores de coordenadas estándar\(e_1,e_2\).
\[ \left.\begin{aligned} T(e_1) \amp= 1.5e_1 = \left(\begin{array}{c}1.5\\0\end{array}\right) \\ T(e_2) \amp= 1.5e_2 = \left(\begin{array}{c}0\\1.5\end{array}\right) \end{aligned}\right\} \implies A = \left(\begin{array}{cc}1.5&0\\0&1.5\end{array}\right). \nonumber \]
Esta es la matriz con la que comenzamos en el Ejemplo 3.1.5 en la Sección 3.1.
Definir\(T\colon\mathbb{R}^2\to\mathbb{R}^2\) por
\[ T(x) = \text{ the vector $x$ rotated counterclockwise by the angle $\theta$}. \nonumber \]
Encuentre la matriz estándar para\(T\).
Solución
Las columnas de\(A\) se obtienen evaluando\(T\) sobre los vectores de coordenadas estándar\(e_1,e_2\). Para poder computar las entradas de\(T(e_1)\) y\(T(e_2)\text{,}\) tenemos que hacer alguna trigonometría.
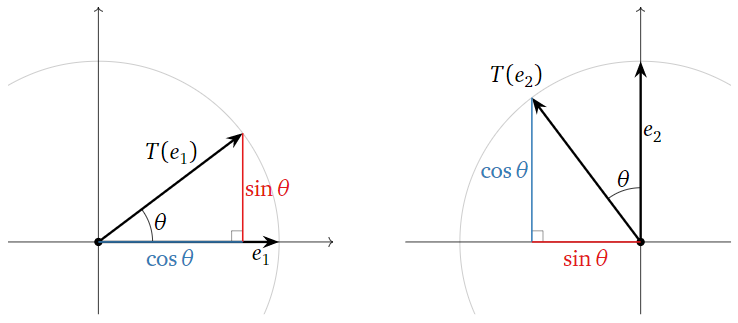
Figura\(\PageIndex{4}\)
Vemos de la imagen que
\[\left.\begin{aligned} T(e_1)&=\left(\begin{array}{c}\color{blue}{\cos\theta}\\ \color{red}{\sin\theta}\end{array}\right) \\ T(e_2)&=\left(\begin{array}{c}{\color{black}{-}\color{red}{\sin\theta}}\\ \color{blue}{\cos\theta}\end{array}\right)\end{aligned}\right\} \implies A=\left(\begin{array}{cc}\color{blue}{\cos\theta}&\color{black}{-}\color{red}{\sin\theta} \\ \color{red}{\sin\theta}&\color{blue}{\cos\theta}\end{array}\right)\nonumber\]
Vimos en el ejemplo anterior que la matriz para la rotación en sentido antihorario del plano por un ángulo de\(\theta\) es
\[A=\left(\begin{array}{cc}\cos\theta &-\sin\theta \\ \sin\theta &\cos\theta\end{array}\right).\nonumber\]
Definir\(T\colon\mathbb{R}^2\to\mathbb{R}^3 \) por la fórmula
\[T\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}3x-y\\y\\x\end{array}\right).\nonumber\]
Encuentre la matriz estándar para\(T\).
Solución
Sustituimos los vectores de coordenadas estándar en la fórmula que define\(T\text{:}\)
\[\left.\begin{aligned} T(e_1)&=T\left(\begin{array}{c}1\\0\end{array}\right)=\left(\begin{array}{c}3(1)-0\\0\\1\end{array}\right)=\left(\begin{array}{c}3\\0\\1\end{array}\right) \\ T(e_2)&=T\left(\begin{array}{c}0\\1\end{array}\right)=\left(\begin{array}{c}3(0)-1\\1\\0\end{array}\right)=\left(\begin{array}{c}-1\\1\\0\end{array}\right)\end{aligned}\right\}\implies A=\left(\begin{array}{cc}3&-1\\0&1\\1&0\end{array}\right).\nonumber\]
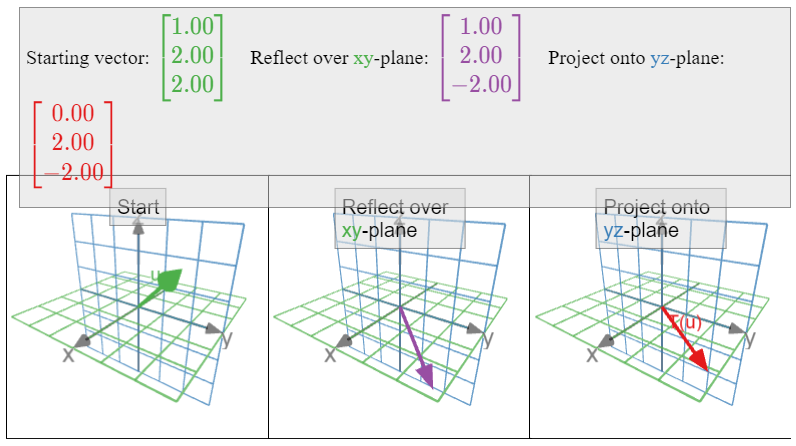
\(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \)Sea la transformación lineal que se refleja sobre el\(xy\) plano y luego se proyecta sobre el\(yz\) plano. ¿Cuál es la matriz estándar para\(T\text{?}\)
Solución
Esta transformación se describe geométricamente, en dos etapas. Para encontrar las columnas de\(A\text{,}\) necesitamos seguir los vectores de coordenadas estándar a través de cada uno de estos pasos.
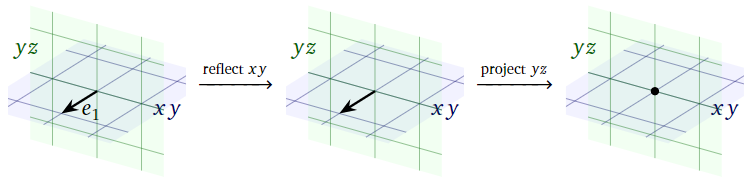
Figura\(\PageIndex{5}\)
Ya que\(e_1\) se encuentra en el\(xy\) plano, reflejarse sobre el\(xy\) plano no se mueve\(e_1\). Dado que\(e_1\) es perpendicular al\(yz\) plano,\(e_1\) proyectarse sobre el\(yz\) plano -lo envía a cero. Por lo tanto,
\[ T(e_1) = \left(\begin{array}{c}0\\0\\0\end{array}\right). \nonumber \]
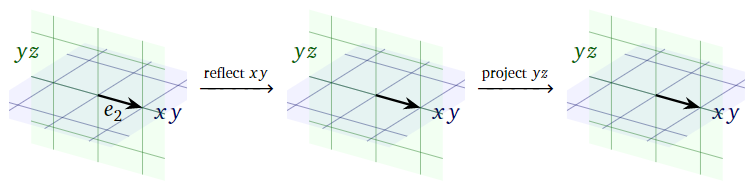
Figura\(\PageIndex{6}\)
Ya que\(e_2\) se encuentra en el\(xy\) plano, reflejarse sobre el\(xy\) plano no se mueve\(e_2\). Dado que\(e_2\) se encuentra en el\(yz\) plano, proyectarse sobre el\(yz\) plano no se mueve\(e_2\) tampoco. Por lo tanto,
\[ T(e_2) = e_2 = \left(\begin{array}{c}0\\1\\0\end{array}\right). \nonumber \]
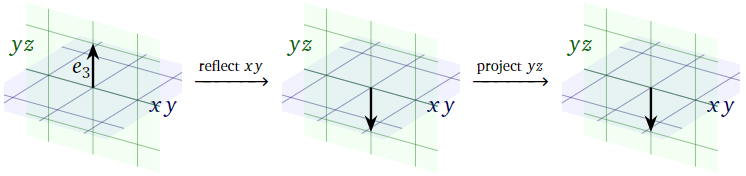
Figura\(\PageIndex{7}\)
Dado que\(e_3\) es perpendicular al\(xy\) -plano, reflejarse sobre el\(xy\) -plano lleva\(e_3\) a su negativo. Ya que\(-e_3\) se encuentra en el\(yz\) plano, proyectarse sobre el\(yz\) plano no lo mueve. Por lo tanto,
\[ T(e_3) = -e_3 = \left(\begin{array}{c}0\\0\\-1\end{array}\right). \nonumber \]
Ahora hemos calculado las tres columnas de\(A\text{:}\)
\[\left.\begin{aligned} T(e_1)&=\left(\begin{array}{c}0\\0\\0\end{array}\right) \\ T(e_2)&=\left(\begin{array}{c}0\\1\\0\end{array}\right) \\ T(e_1)&=\left(\begin{array}{c}0\\0\\-1\end{array}\right) \end{aligned}\right\} \implies A=\left(\begin{array}{ccc}0&0&0\\0&1&0\\0&0&-1\end{array}\right).\nonumber\]
Recordemos de la Definición 3.1.2 en la Sección 3.1 que la transformación de identidad es la transformación\(\text{Id}_{\mathbb{R}^n }\colon\mathbb{R}^n \to\mathbb{R}^n \) definida por\(\text{Id}_{\mathbb{R}^n }(x) = x\) para cada vector\(x\).
Verifique que la transformación de identidad\(\text{Id}_{\mathbb{R}^n }\colon\mathbb{R}^n \to\mathbb{R}^n \) sea lineal y calmente su matriz estándar.
Solución
Verificamos las dos propiedades definitorias, Definición\(\PageIndex{1}\), de transformaciones lineales. Dejen\(u,v\) ser vectores en\(\mathbb{R}^n \). Entonces
\[\text{Id}_{\mathbb{R}^n}(u+v)=u+v=\text{Id}_{\mathbb{R}^n}(u)+\text{Id}_{\mathbb{R}^n}(v).\nonumber\]
Si\(c\) es un escalar, entonces
\[ \text{Id}_{\mathbb{R}^n }(cu) = cu = c\text{Id}_{\mathbb{R}^n }(u). \nonumber \]
Dado que\(\text{Id}_{\mathbb{R}^n }\) satisface las dos propiedades definitorias, se trata de una transformación lineal.
Ahora que sabemos que\(\text{Id}_{\mathbb{R}^n }\) es lineal, tiene sentido computar su matriz estándar. Para cada vector de coordenadas estándar\(e_i\text{,}\) tenemos\(\text{Id}_{R^n}(e_i) = e_i\). En otras palabras, las columnas de la matriz estándar de\(\text{Id}_{\mathbb{R}^n }\) son los vectores de coordenadas estándar, por lo que la matriz estándar es la matriz de identidad
\[I_n=\left(\begin{array}{ccccc}1&0&\cdots&0&0\\0&1&\cdots&0&0\\ \vdots&\vdots&\ddots&\vdots&\vdots \\ 0&0&\cdots &1&1\\0&0&\cdots &0&1\end{array}\right).\nonumber\]
Se computó en Ejemplo\(\PageIndex{11}\) que la matriz de la transformada de identidad es la matriz de identidad: para cada\(x\) en\(\mathbb{R}^n \text{,}\)
\[ x = \text{Id}_{\mathbb{R}^n }(x) = I_nx. \nonumber \]
Por lo tanto,\(I_nx=x\) para todos\(x\text{:}\) los vectores el producto de la matriz de identidad y un vector es el mismo vector.


