3.4: Multiplicación Matricial
- Page ID
- 113098
- Comprender las composiciones de las transformaciones.
- Comprender la relación entre los productos matriciales y las composiciones de las transformaciones matriciales.
- Estar cómodo haciendo álgebra básica involucrando matrices.
- Receta: multiplicación matricial (dos vías).
- Cuadro: composición de transformaciones.
- Vocabulario palabra: composición.
En esta sección, estudiamos composiciones de transformaciones. Como veremos, la composición es una forma de encadenar transformaciones juntas. La composición de las transformaciones matriciales corresponde a una noción de multiplicar dos matrices juntas. También discutimos la adición y multiplicación escalar de transformaciones y de matrices.
Composición de Transformaciones Lineales
Composición significa lo mismo en álgebra lineal que en Cálculo. Aquí está la definición.
Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) y\(U\colon\mathbb{R}^p \to\mathbb{R}^n \) ser transformaciones. Su composición es la transformación\(T\circ U\colon\mathbb{R}^p \to\mathbb{R}^m \) definida por
\[ (T\circ U)(x) = T(U(x)). \nonumber \]
Componer dos transformaciones significa encadenarlas:\(T\circ U\) es la transformación que primero aplica\(U\text{,}\) luego aplica\(T\) (anotar el orden de las operaciones). Más precisamente, para evaluar\(T\circ U\) en un vector de entrada\(x\text{,}\) primero evalúas\(U(x)\text{,}\) luego tomas este vector de salida\(U\) y lo usas como vector de entrada de\(T\text{:}\) eso es,\((T\circ U)(x) = T(U(x))\). Por supuesto, esto sólo tiene sentido cuando las salidas de\(U\) son entradas válidas de es\(T\text{,}\) decir, cuando el rango de\(U\) está contenido en el dominio de\(T\).
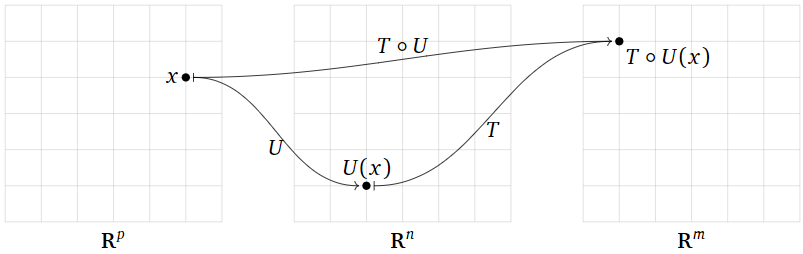
Figura\(\PageIndex{1}\)
Aquí hay una imagen de la composición\(T\circ U\) como una “máquina” que primero se ejecuta\(U\text{,}\) luego toma su salida y la alimenta en\(T\text{;}\) hay una imagen similar en Subsección Transformaciones en la Sección 3.1.
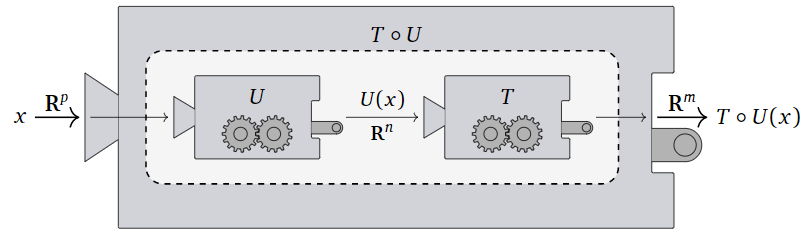
Figura\(\PageIndex{2}\)
- \(T\circ U\)Para que se defina, el codominio de\(U\) debe ser igual al dominio de\(T\).
- El dominio de\(T\circ U\) es el dominio de\(U\).
- El codominio de\(T\circ U\) es el codominio de\(T\).
Definir\(f\colon \mathbb{R} \to\mathbb{R} \) por\(f(x) = x^2\) y\(g\colon \mathbb{R} \to\mathbb{R} \) por\(g(x) = x^3\). La composición\(f\circ g\colon \mathbb{R} \to\mathbb{R} \) es la transformación definida por la regla
\[ f\circ g(x) = f(g(x)) = f(x^3) = (x^3)^2 = x^6. \nonumber \]
Por ejemplo,\(f\circ g(-2) = f(-8) = 64.\)
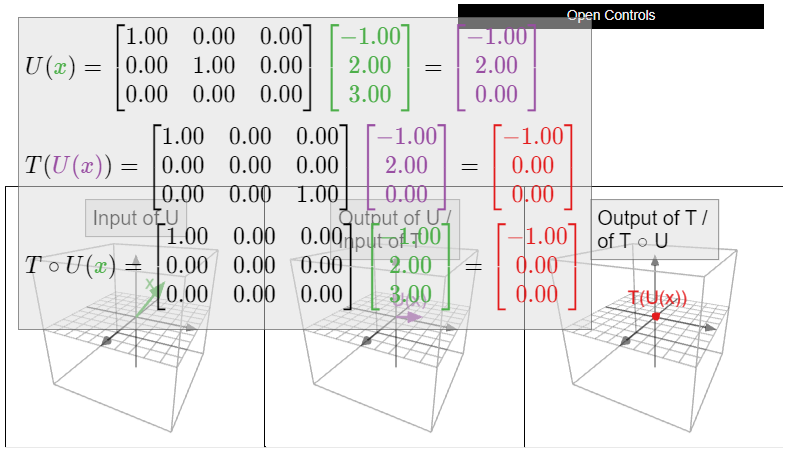
Definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) y\(U\colon\mathbb{R}^2 \to\mathbb{R}^3 \) por
\[T(x)=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)x\quad\text{and}\quad U(x)=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right)x.\nonumber\]
Su composición es una transformación\(T\circ U\colon\mathbb{R}^2 \to\mathbb{R}^2 \text{;}\) resulta ser la transformación matricial asociada a la matriz\(\bigl(\begin{smallmatrix}1\amp1\\1\amp1\end{smallmatrix}\bigr)\).
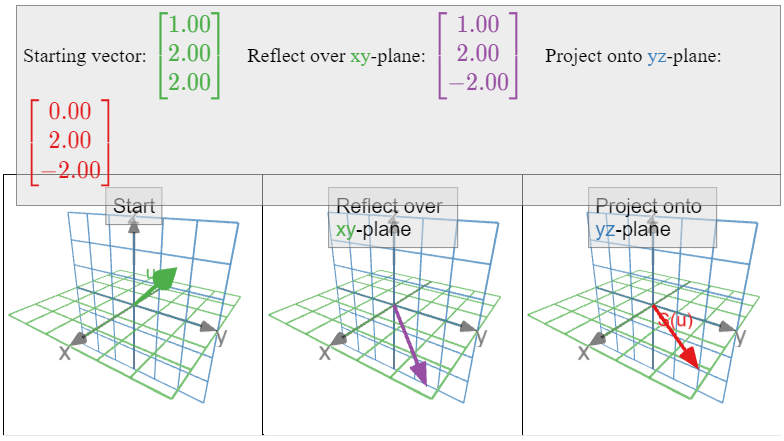
\(S\colon\mathbb{R}^3 \to\mathbb{R}^3 \)Sea la transformación lineal que primero se refleja sobre el\(xy\) plano y luego se proyecta sobre el\(yz\) plano, como en el Ejemplo 3.3.10 de la Sección 3.3. La transformación\(S\) es la composición\(T\circ U\text{,}\) donde\(U\colon\mathbb{R}^3 \to\mathbb{R}^3 \) está la transformación que se refleja sobre el\(xy\) plano, y\(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \) es la transformación que se proyecta sobre el\(yz\) plano.
\(S\colon\mathbb{R}^3 \to\mathbb{R}^3 \)Sea la transformación lineal que primero se proyecta sobre el\(xy\) plano, y luego se proyecta sobre el\(xz\) plano. La transformación\(S\) es la composición\(T\circ U\text{,}\) donde\(U\colon\mathbb{R}^3 \to\mathbb{R}^3 \) está la transformación que se proyecta sobre el\(xy\) plano, y\(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \) es la transformación que se proyecta sobre el\(xz\) plano.
Recordemos de la Definición 3.1.2 en la Sección 3.1 que la transformación de identidad es la transformación\(\operatorname{Id}_{\mathbb{R}^n }\colon\mathbb{R}^n \to\mathbb{R}^n \) definida por\(\operatorname{Id}_{\mathbb{R}^n }(x) = x\) para cada vector\(x\).
\(S,T,U\)Dejen ser transformaciones y dejar\(c\) que sean un escalar. Supongamos que\(T\colon\mathbb{R}^n \to\mathbb{R}^m \text{,}\) y que en cada una de las siguientes identidades, los dominios y los codominios son compatibles cuando sea necesario para que se defina la composición. Las siguientes propiedades son fácilmente verificadas:
\[\begin{align*} S\circ(T+U) \amp= S\circ T+S\circ U \amp (S + T)\circ U \amp= S\circ U + T\circ U \amp\\ c(T\circ U) \amp= (cT)\circ U \amp c(T\circ U) \amp= T\circ(cU) \rlap{\;\;\text{ if $T$ is linear}}\\ T\circ\operatorname{Id}_{\mathbb{R}^n } \amp= T \amp \operatorname{Id}_{\mathbb{R}^m }\circ T \amp= T\\ \amp \amp S\circ(T\circ U) \amp= (S\circ T)\circ U \amp \end{align*}\]
La propiedad final se llama asociatividad. Desenvolviendo ambos lados, dice:
\[ S\circ(T\circ U)(x) = S(T\circ U(x)) = S(T(U(x))) = S\circ T(U(x)) = (S\circ T)\circ U(x). \nonumber \]
En otras palabras, ambos\(S\circ (T\circ U)\) y\((S\circ T)\circ U\) son la transformación definida aplicando primero\(U\text{,}\) luego\(T\text{,}\) luego\(S\).
La composición de las transformaciones no es conmutativa en general. Es decir, en general,\(T\circ U\neq U\circ T\text{,}\) incluso cuando ambas composiciones están definidas.
Definir\(f\colon \mathbb{R} \to\mathbb{R} \) por\(f(x) = x^2\) y\(g\colon \mathbb{R} \to\mathbb{R} \) por\(g(x) = e^x\). La composición\(f\circ g\colon \mathbb{R} \to\mathbb{R} \) es la transformación definida por la regla
\[ f\circ g(x) = f(g(x)) = f(e^x) = (e^x)^2 = e^{2x}. \nonumber \]
La composición\(g\circ f\colon \mathbb{R} \to\mathbb{R} \) es la transformación definida por la regla
\[ g\circ f(x) = g(f(x)) = g(x^2) = e^{x^2}. \nonumber \]
Tenga\(e^{x^2}\neq e^{2x}\) en cuenta que en general; por ejemplo, si\(x=1\) entonces\(e^{x^2} = e\) y\(e^{2x} = e^2\). Así no\(f \circ g\) es igual a\(g \circ f\text{,}\) y ya podemos ver con funciones de una variable que la composición de funciones no es conmutativa.
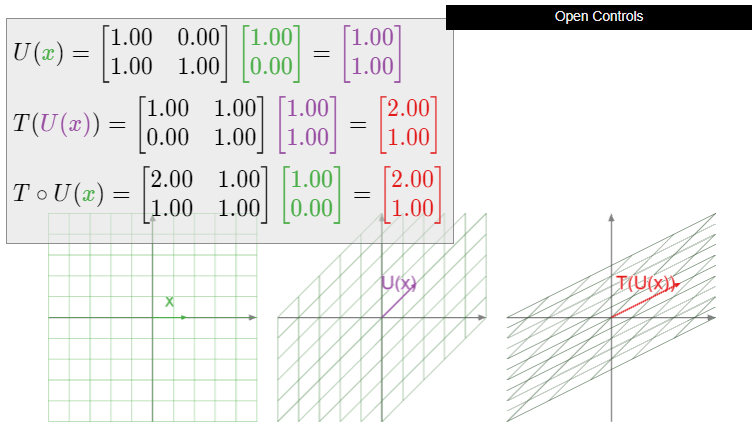
Definir transformaciones matriciales\(T,U\colon\mathbb{R}^2 \to\mathbb{R}^2 \) mediante
\[ T(x) = \left(\begin{array}{cc}1&1\\0&1\end{array}\right)x \quad\text{and}\quad U(x) = \left(\begin{array}{cc}1&0\\1&1\end{array}\right)x. \nonumber \]
Geométricamente,\(T\) es una cizalla en la\(x\) dirección -y\(U\) es una cizalla en la\(Y\) dirección -dirección. Evaluamos
\[T\circ U\left(\begin{array}{c}1\\0\end{array}\right)=T\left(\begin{array}{c}1\\1\end{array}\right)=\left(\begin{array}{c}2\\1\end{array}\right)\nonumber\]
y
\[ U\circ T\left(\begin{array}{c}1\\0\end{array}\right) = U\left(\begin{array}{c}1\\0\end{array}\right) = \left(\begin{array}{c}1\\1\end{array}\right). \nonumber \]
Dado que\(T\circ U\) y\(U\circ T\) tienen diferentes salidas para el vector de entrada\(1\choose 0\text{,}\) son diferentes transformaciones. (Ver este Ejemplo\(\PageIndex{9}\).)
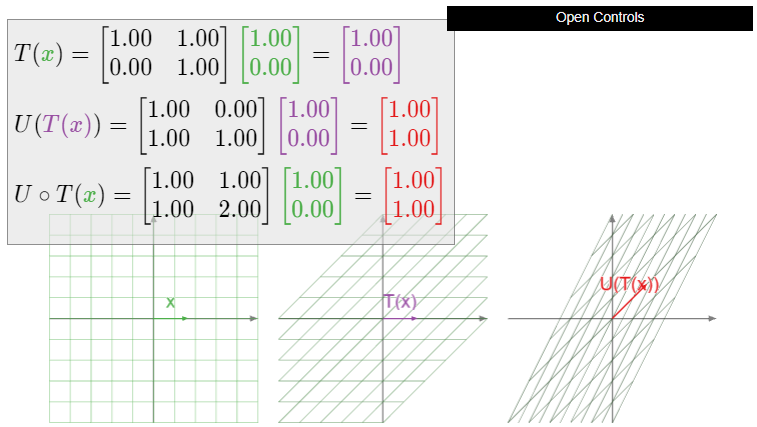
Figura\(\PageIndex{7}\): Ilustración de la composición\(U\circ T\).
Multiplicación matricial
En esta subsección, se introduce una operación aparentemente no relacionada sobre matrices, es decir, la multiplicación matricial. Como veremos en la siguiente subsección, la multiplicación matricial corresponde exactamente a la composición de las transformaciones lineales correspondientes. Primero necesitamos algo de terminología.
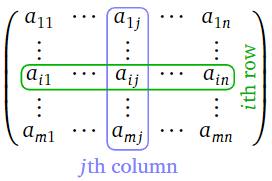
\(A\)Déjese ser una\(m\times n\) matriz. Generalmente escribiremos\(a_{ij}\) para la entrada en la fila\(i\) th y la\(j\) th columna. Se llama la \(i,j\)entrada de la matriz.
Figura\(\PageIndex{8}\)
Dejar\(A\) ser una\(m\times n\) matriz y dejar\(B\) ser una\(n\times p\) matriz. Denotar las columnas de\(B\) por\(v_1,v_2,\ldots,v_p\text{:}\)
\[B=\left(\begin{array}{cccc}|&|&\quad&| \\ v_1&v_2&\cdots &v_p \\ |&|&\quad&|\end{array}\right).\nonumber\]
El producto\(AB\) es la\(m\times p\) matriz con columnas\(Av_1,Av_2,\ldots,Av_p\text{:}\)
\[AB=\left(\begin{array}{cccc}|&|&\quad&| \\ Av_1&Av_2&\cdots &Av_p \\ |&|&\quad &|\end{array}\right).\nonumber\]
En otras palabras, la multiplicación matricial se define columna por columna, o “distribuye sobre las columnas de”\(B\).
\[\begin{aligned}\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right)&=\left(\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)\left(\begin{array}{c}1\\0\\1\end{array}\right)\:\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)\left(\begin{array}{c}0\\1\\0\end{array}\right)\right) \\ &=\left(\left(\begin{array}{c}1\\1\end{array}\right)\:\left(\begin{array}{c}1\\1\end{array}\right)\right)=\left(\begin{array}{cc}1&1\\1&1\end{array}\right)\end{aligned}\nonumber\]
Para\(Av_1,Av_2,\ldots,Av_p\) que se definan los vectores, el número de filas de\(B\) tiene que ser igual al número de columnas de\(A\).
- \(AB\)Para que se defina, el número de filas de\(B\) tiene que ser igual al número de columnas de\(A\).
- El producto de una\(\color{blue}{m}\color{black}{\times}\color{Red}{n}\) matriz y una\(\color{red}{n}\color{black}{\times}\color{blue}{p}\) matriz es una\(\color{blue}{m}\color{black}{\times}\color{blue}{p}\) matriz.
Si solo\(B\) tiene una columna, entonces\(AB\) también tiene una columna. Una matriz con una columna es igual que un vector, por lo que la definición del producto matriz generaliza la definición del producto matriz-vector a partir de la Definición 2.3.1 en la Sección 2.3.
Si\(A\) es una matriz cuadrada, entonces podemos multiplicarla por sí misma; definimos sus poderes para que sean
\[ A^2 = AA \qquad A^3 = AAA \qquad \text{etc.} \nonumber \]
La regla de fila-columna para la multiplicación matricial
Recordemos de la Definición 2.3.3 en la Sección 2.3 que el producto de un vector de fila y un vector de columna es el escalar
\[ \left(\begin{array}{cccc}a_1&a_2&\cdots &a_n\end{array}\right)\:\left(\begin{array}{c}x_1\\x_2\\ \vdots\\x_n\end{array}\right) = a_1x_1 + a_2x_2 + \cdots + a_nx_n. \nonumber \]
El siguiente procedimiento para encontrar el producto de la matriz se adapta mucho mejor a los cálculos a mano; la Definición anterior\(\PageIndex{3}\) es más adecuada para probar teoremas, como este Teorema\(\PageIndex{1}\) a continuación.
Dejar\(A\) ser una\(m\times n\) matriz, dejar\(B\) ser una\(n\times p\) matriz, y dejar\(C = AB\). Entonces la\(ij\) entrada de\(C\) es la fila\(i\) th de\(A\) veces la\(j\) th columna de\(B\text{:}\)
\[ c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj}. \nonumber \]
Aquí hay un diagrama:

Figura\(\PageIndex{9}\)
La regla fila-columna para la multiplicación matriz-vector en la Sección 2.3, Receta: La regla de fila-columna para la multiplicación matriz-vector, dice que si\(A\) tiene filas\(r_1,r_2,\ldots,r_m\) y\(x\) es un vector, entonces
\[Ax=\left(\begin{array}{c}—r_1— \\ —r_2— \\ \vdots \\ —r_m—\end{array}\right)x=\left(\begin{array}{c}r_1x \\ r_2x \\ \vdots \\ r_mx\end{array}\right).\nonumber\]
La definición\(\PageIndex{3}\) de multiplicación matricial es
\[A\left(\begin{array}{cccc}|&|&\quad&| \\ c_1&c_2&\cdots &c_p \\ |&|&\quad &| \end{array}\right)=\left(\begin{array}{cccc}|&|&\quad&| \\ Ac_1&Ac_2&\cdots &Ac_p \\ |&|&\quad &\end{array}\right).\nonumber\]
De ello se deduce que
\[\left(\begin{array}{c}—r_1— \\ —r_2— \\ \vdots \\ —r_m—\end{array}\right)\:\left(\begin{array}{cccc}|&|&\quad&| \\ c_1&c_2&\cdots &c_p \\ |&|&\quad &| \end{array}\right) =\left(\begin{array}{cccc}r_1c_1&r_1c_2&\cdots &r_1c_p \\ r_2c_1&r_2c_2&\cdots &r_2c_p \\ \vdots& \vdots &{}&\vdots \\ r_mc_1&r_mc_2 &\cdots &r_mc_p\end{array}\right).\nonumber\]
La regla fila-columna nos permite calcular la matriz del producto una entrada a la vez:
\[\begin{aligned}\left(\begin{array}{ccc}\color{Green}{1}&\color{Green}{2}&\color{Green}{3} \\ \color{black}{4}&\color{black}{5}&\color{black}{6}\end{array}\right)\:\left(\begin{array}{cc}\color{blue}{1}&\color{black}{-3} \\ \color{blue}{2}&\color{black}{-2} \\ \color{blue}{3}&\color{black}{-1}\end{array}\right) &= \left(\begin{array}{cccccc} \color{Green}{1} \color{black}{\cdot}\color{blue}{1}&\color{black}{+}&\color{Green}{2}\color{black}{\cdot}\color{blue}{2}&\color{black}{+}&\color{Green}{3}\color{black}{\cdot}\color{blue}{3}&\fbox{ } \\ {}&{}&\fbox{ }&{}&{}&\fbox{ }\end{array}\right) = \left(\begin{array}{cc}\color{purple}{14}&\color{black}{\fbox{ }} \\ \fbox{ }&\fbox{ }\end{array}\right) \\ \left(\begin{array}{ccc}1&2&3 \\ \color{Green}{4}&\color{Green}{5}&\color{Green}{6}\end{array}\right)\left(\begin{array}{cc}\color{blue}{1}&\color{black}{-3}\\ \color{blue}{2}&\color{black}{-2} \\ \color{blue}{3}&\color{black}{-1}\end{array}\right)&=\left(\begin{array}{cccccc} {}&{}&\fbox{ }&{}&{}&\fbox{ } \\ \color{Green}{4}\color{black}{\cdot}\color{blue}{1}&\color{black}{+}&\color{Green}{5}\color{black}{\cdot}\color{blue}{2}&\color{black}{+}&\color{Green}{6}\color{black}{\cdot}\color{blue}{3}&\fbox{ }\end{array}\right)=\left(\begin{array}{cc}14&\fbox{ }\\ \color{purple}{32}&\color{black}{\fbox{ }}\end{array}\right) \end{aligned}\]
¡Deberías intentar rellenar las otras dos cajas!
Aunque la multiplicación matricial satisface muchas de las propiedades que uno esperaría (ver el final de la sección), hay que tener cuidado al hacer la aritmética matricial, ya que hay varias propiedades que no se satisfacen en general.
- La multiplicación matricial no es conmutativa:\(AB\) no suele ser igual a\(BA\text{,}\) incluso cuando ambos productos están definidos y tienen el mismo tamaño. Ver Ejemplo\(\PageIndex{9}\).
- La multiplicación matricial no satisface la ley de cancelación:\(AB=AC\) no implica\(B=C\text{,}\) ni siquiera cuando\(A\neq 0\). Por ejemplo,
\[\left(\begin{array}{cc}1&0\\0&0\end{array}\right)\left(\begin{array}{cc}1&2\\3&4\end{array}\right)=\left(\begin{array}{cc}1&2\\0&0\end{array}\right)=\left(\begin{array}{cc}1&0\\0&0\end{array}\right)\left(\begin{array}{cc}1&2\\5&6\end{array}\right).\nonumber\] - Es posible para\(AB=0\text{,}\) incluso cuando\(A\neq 0\) y\(B\neq 0\). Por ejemplo,
\[\left(\begin{array}{cc}1&0\\1&0\end{array}\right)\left(\begin{array}{cc}0&0\\1&1\end{array}\right)=\left(\begin{array}{cc}0&0\\0&0\end{array}\right).\nonumber\]
Si bien la multiplicación matricial no es conmutativa en general hay ejemplos de matrices\(A\) y\(B\) con\(AB=BA\). Por ejemplo, esto siempre funciona cuando\(A\) es la matriz cero, o cuando\(A=B\). Se anima al lector a encontrar otros ejemplos.
Considerar las matrices
\[A=\left(\begin{array}{cc}1&1\\0&1\end{array}\right)\quad\text{and}\quad B=\left(\begin{array}{cc}1&0\\1&1\end{array}\right),\nonumber\]
como en este Ejemplo\(\PageIndex{6}\). La matriz\(AB\) es
\[\left(\begin{array}{cc}1&1\\0&1\end{array}\right)\:\left(\begin{array}{cc}1&0\\1&1\end{array}\right)=\left(\begin{array}{cc}2&1\\1&1\end{array}\right),\nonumber\]
mientras que la matriz\(BA\) es
\[\left(\begin{array}{cc}1&0\\1&1\end{array}\right)\:\left(\begin{array}{cc}1&1\\0&1\end{array}\right)=\left(\begin{array}{cc}1&1\\1&2\end{array}\right).\nonumber\]
En particular, tenemos
\[ AB \neq BA. \nonumber \]
Y así la multiplicación matricial no siempre es conmutativa. No es casualidad que este ejemplo concuerde con el Ejemplo anterior\(\PageIndex{6}\); estamos a punto de ver que la multiplicación de matrices corresponde a la composición de las transformaciones.
Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) y\(U\colon\mathbb{R}^p \to\mathbb{R}^n \) ser transformaciones lineales, y dejar\(A\) y\(B\) ser sus matrices estándar, respectivamente. Recordemos que\(T\circ U(x)\) es el vector obtenido aplicando primero\(U\) a\(x\text{,}\) y después\(T\).
En el lado de la matriz, la matriz estándar de\(T\circ U\) es el producto\(AB\text{,}\) así\(T\circ U(x) = (AB)x\). Por asociatividad de multiplicación matricial, tenemos\((AB)x = A(Bx)\text{,}\) así que el producto\((AB)x\) puede calcularse multiplicando primero\(x\) por\(B\text{,}\) luego multiplicando el producto por\(A\).
Por lo tanto, la multiplicación matricial ocurre en el mismo orden que la composición de las transformaciones. Es decir, tanto las matrices como las transformaciones están escritas en el orden opuesto al orden en que actúan. Pero la multiplicación matricial y la composición de las transformaciones se escriben en el mismo orden entre sí: la matriz para\(T\circ U\) es\(AB\).
Composición y Multiplicación Matricial
El punto de esta subsección es mostrar que la multiplicación matricial corresponde a la composición de las transformaciones, es decir, la matriz estándar para\(T \circ U\) es el producto de las matrices estándar para\(T\) y para\(U\). ¡Debería ser difícil creer que nuestra complicada fórmula para la multiplicación matricial realmente signifique algo intuitivo como “encadenar dos transformaciones juntas”!
Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) y\(U\colon\mathbb{R}^p \to\mathbb{R}^n \) ser transformaciones lineales, y dejar\(A\) y\(B\) ser sus matrices estándar, respectivamente, así\(A\) es una\(m\times n\) matriz y\(B\) es una\(n\times p\) matriz. Entonces\(T\circ U\colon\mathbb{R}^p \to\mathbb{R}^m \) es una transformación lineal, y su matriz estándar es el producto\(AB\).
- Prueba
-
Primero verificamos que\(T\circ U\) sea lineal. Dejen\(u,v\) ser vectores adentro\(\mathbb{R}^p \). Entonces
\[ \begin{aligned} T\circ U(u+v) &= T(U(u+v)) = T(U(u)+U(v)) \\ &= T(U(u))+T(U(v)) = T\circ U(u) + T\circ U(v). \end{aligned} \]
Si\(c\) es un escalar, entonces
\[ T\circ U(cv) = T(U(cv)) = T(cU(v)) = cT(U(v)) = cT\circ U(v). \nonumber \]
Dado que\(T\circ U\) satisface las dos propiedades definitorias, Definición 3.3.1 en la Sección 3.3, es una transformación lineal.
Ahora que sabemos que\(T\circ U\) es lineal, tiene sentido computar su matriz estándar. Dejar\(C\) ser la matriz estándar de\(T\circ U\text{,}\) así\(T(x) = Ax,\)\(U(x) = Bx\text{,}\) y\(T\circ U(x) = Cx\). Por Teorema 3.3.1 en la Sección 3.3, la primera columna de\(C\) es\(Ce_1\text{,}\) y la primera columna de\(B\) es\(Be_1\). Tenemos
\[ T\circ U(e_1) = T(U(e_1)) = T(Be_1) = A(Be_1). \nonumber \]
Por definición, la primera columna del producto\(AB\) es el producto de\(A\) con la primera columna de la\(B\text{,}\) cual es\(Be_1\text{,}\) tan
\[ Ce_1 = T\circ U(e_1) = A(Be_1) = (AB)e_1. \nonumber \]
De ello se deduce que\(C\) tiene la misma primera columna que\(AB\). El mismo argumento aplicado al\(i\) th vector de coordenadas estándar\(e_i\) muestra eso\(C\) y\(AB\) tienen la misma\(i\) ésima columna; ya que tienen las mismas columnas, son la misma matriz.
El teorema justifica nuestra elección de definición del producto matriz. Esta es la única razón por la que los productos de matriz se definen de esta manera. Para replantear:
La matriz de la composición de dos transformaciones lineales es el producto de las matrices de las transformaciones.
En el Ejemplo 3.3.8 de la Sección 3.3, mostramos que la matriz estándar para la rotación en sentido antihorario del plano por un ángulo de\(\theta\) es
\[A=\left(\begin{array}{cc}\cos\theta &-\sin\theta \\ \sin\theta &\cos\theta\end{array}\right).\nonumber\]
Dejar\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser rotación en sentido antihorario por\(45^\circ\text{,}\) y dejar\(U\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser rotación en sentido antihorario por\(90^\circ\). Las matrices\(A\) y\(B\) para\(T\) y\(U\) son, respectivamente,
\[\begin{aligned}A&=\left(\begin{array}{cc}\cos(45^\circ )&-\sin (45^\circ ) \\ \sin (45^\circ)&\cos (45^\circ)\end{array}\right) =\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1&-1\\1&1\end{array}\right) \\ B&=\left(\begin{array}{cc}\cos(90^\circ )&-\sin (90^\circ ) \\ \sin (90^\circ)&\cos (90^\circ)\end{array}\right) =\left(\begin{array}{cc}0&-1\\1&0\end{array}\right). \end{aligned}\]
Aquí utilizamos las identidades trigonométricas
\ begin {alinear*}\ cos (45^\ circ)\ amp=\ frac 1 {\ sqrt2}\ amp\ sin (45^\ circ)\ amp=\ frac 1 {\ sqrt2}\\ cos (90^\ circ)\ amp= 0\ amp\ sin (90^\ circ)\ amp= 1. \ end {alinear*}
La matriz estándar de la composición\(T\circ U\) es
\[AB=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1&-1\\1&1\end{array}\right)\left(\begin{array}{cc}0&-1\\1&0\end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}-1&-1\\1&-1\end{array}\right).\nonumber\]
Esto es consistente con el hecho de que\(T\circ U\) es la rotación en sentido antihorario por que\(90^\circ + 45^\circ = 135^\circ\text{:}\) tenemos
\[\left(\begin{array}{cc}\cos(135^\circ )&-\sin (135^\circ ) \\ \sin (135^\circ)&\cos (135^\circ)\end{array}\right) =\frac{1}{\sqrt{2}}\left(\begin{array}{cc}-1&-1\\1&-1\end{array}\right) \nonumber\]
porque\(\cos(135^\circ) = -1/\sqrt2\) y\(\sin(135^\circ) = 1/\sqrt2\).
Derivar las identidades trigonométricas
\[ \sin(\alpha\pm\beta) = \sin(\alpha)\cos(\beta) \pm \cos(\alpha)\sin(\beta) \nonumber \]
y
\[ \cos(\alpha\pm\beta) = \cos(\alpha)\cos(\beta) \mp \sin(\alpha)\sin(\beta) \nonumber \]
utilizando el Teorema anterior\(\PageIndex{1}\) tal como se aplica a las transformaciones de rotación, como en el ejemplo anterior.
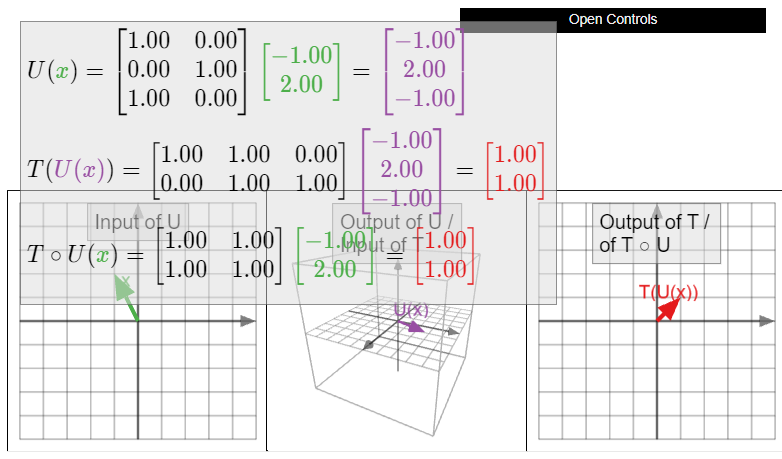
Definir\(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) y\(U\colon\mathbb{R}^2 \to\mathbb{R}^3 \) por
\[T(x)=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)x\quad\text{and}\quad U(x)=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right)x.\nonumber\]
Su composición es una transformación lineal\(T\circ U\colon\mathbb{R}^2 \to\mathbb{R}^2 \). Por el Teorema\(\PageIndex{1}\), su matriz estándar es
\[\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right)=\left(\begin{array}{cc}1&1\\1&1\end{array}\right),\nonumber\]
como calculamos en el Ejemplo anterior\(\PageIndex{7}\).
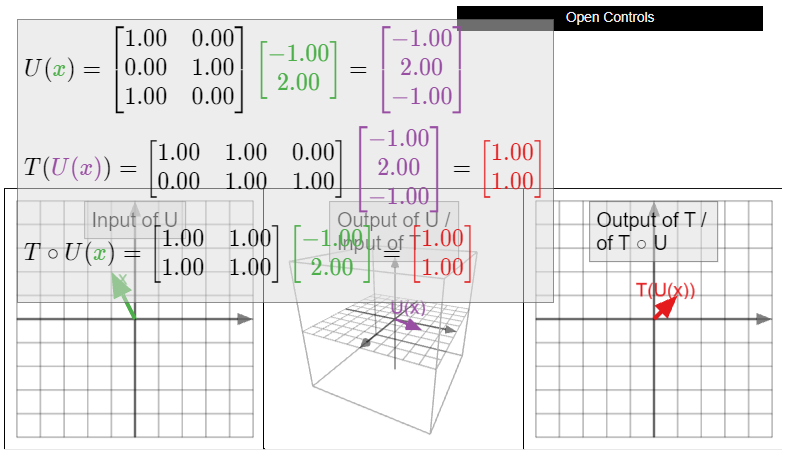
\(S\colon\mathbb{R}^3 \to\mathbb{R}^3 \)Sea la transformación lineal que primero se refleja sobre el\(xy\) plano y luego se proyecta sobre el\(yz\) plano, como en el Ejemplo 3.3.10 de la Sección 3.3. La transformación\(S\) es la composición\(T\circ U\text{,}\) donde\(U\colon\mathbb{R}^3 \to\mathbb{R}^3 \) está la transformación que se refleja sobre el\(xy\) plano, y\(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \) es la transformación que se proyecta sobre el\(yz\) plano.
Calculemos la matriz\(B\) para\(U\).
Figura\(\PageIndex{11}\)
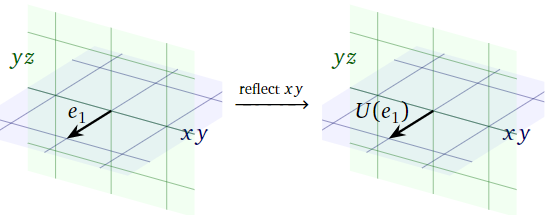
Ya que\(e_1\) se encuentra en el\(xy\) plano, reflejarlo sobre el\(xy\) plano no lo mueve:
\[ U(e_1) = \left(\begin{array}{c}1\\0\\0\end{array}\right). \nonumber \]
Figura\(\PageIndex{12}\)
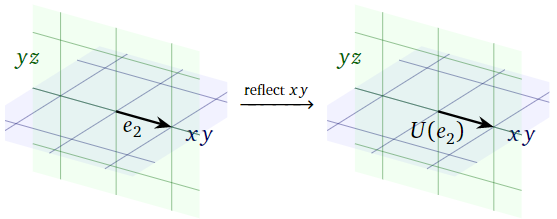
Dado que\(e_2\) se encuentra en el\(xy\) plano, reflejarse sobre el\(xy\) plano no lo mueve tampoco:
\[ U(e_2) = e_2 = \left(\begin{array}{c}0\\1\\0\end{array}\right). \nonumber \]
Figura\(\PageIndex{13}\)
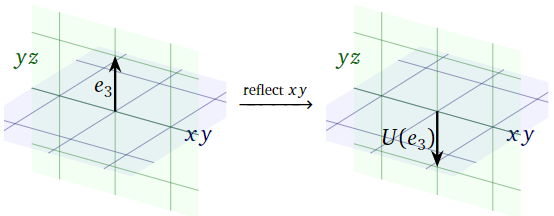
Dado que\(e_3\) es perpendicular al\(xy\) plano, reflejarse sobre el\(xy\) plano toma\(e_3\) a su negativo:
\[ U(e_3) = -e_3 = \left(\begin{array}{c}0\\0\\-1\end{array}\right). \nonumber \]
Hemos calculado todas las columnas de\(B\text{:}\)
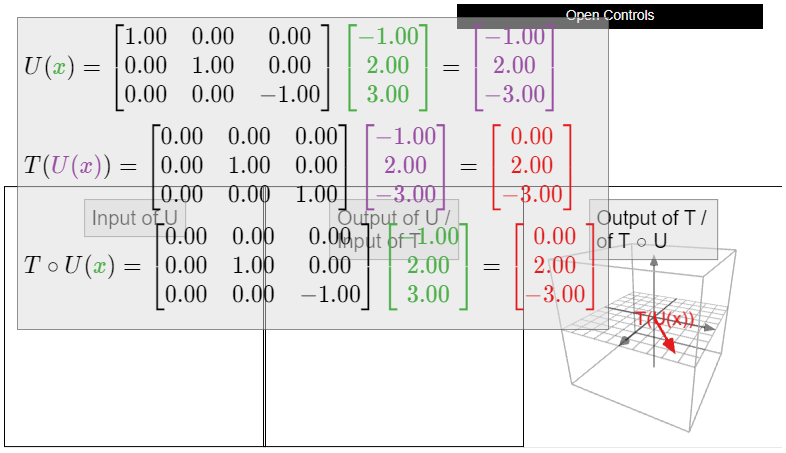
\[B=\left(\begin{array}{ccc}|&|&| \\ U(e_1)&U(e_2)&U(e_3) \\ |&|&|\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&-1\end{array}\right).\nonumber\]
Por un método similar, encontramos
\[A=\left(\begin{array}{ccc}0&0&0\\0&1&0\\0&0&1\end{array}\right).\nonumber\]
De ello se deduce que la matriz para\(S = T\circ U\) es
\[\begin{aligned} AB&=\left(\begin{array}{ccc}0&0&0\\0&1&0\\0&0&1\end{array}\right)\:\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&-1\end{array}\right) \\ &=\left(\left(\begin{array}{ccc}0&0&0\\0&1&0\\0&0&1\end{array}\right)\left(\begin{array}{c}1\\0\\0\end{array}\right)\:\:\left(\begin{array}{ccc}0&0&0\\0&1&0\\0&0&1\end{array}\right)\left(\begin{array}{c}0\\1\\0\end{array}\right)\:\:\left(\begin{array}{ccc}0&0&0\\0&1&0\\0&0&1\end{array}\right)\left(\begin{array}{c}0\\0\\-1\end{array}\right)\right) \\ &=\left(\begin{array}{ccc}0&0&0\\0&1&0\\0&0&-1\end{array}\right),\end{aligned}\]
como calculamos en el Ejemplo 3.3.10 en la Sección 3.3.
Recordemos de la Definición 3.3.2 en la Sección 3.3 que la matriz de identidad es la\(n\times n\) matriz\(I_n\) cuyas columnas son los vectores de coordenadas estándar en\(\mathbb{R}^n \). La matriz de identidad es la matriz estándar de la transformación de identidad: es decir,\(x = \operatorname{Id}_{\mathbb{R}^n }(x) = I_nx\) para todos los vectores\(x\) en\(\mathbb{R}^n \). Para cualquier transformación lineal\(T : \mathbb{R}^n \to \mathbb{R}^m \) tenemos
\[ I_{\mathbb{R}^m } \circ T = T \nonumber \]
y por el mismo token tenemos para cualquier\(m \times n\) matriz\(A\) que tengamos
\[ I_mA=A\text{.} \nonumber \]
De igual manera, tenemos\(T \circ I_{\mathbb{R}^n } = T\) y\(AI_n=A\).
El álgebra de transformaciones y matrices
En esta subsección describimos dos operaciones más que se pueden realizar sobre las transformaciones: suma y multiplicación escalar. Luego traducimos estas operaciones al lenguaje de las matrices. Esto es análogo a lo que hicimos para la composición de transformaciones lineales, pero mucho menos sutil.
- \(T,U\colon\mathbb{R}^n \to\mathbb{R}^m \)Dejen ser dos transformaciones. Su suma es la transformación\(T+U\colon\mathbb{R}^n \to\mathbb{R}^m \) definida por
\[(T+U)(x)=T(x)+U(x).\nonumber\]
Note que la adición de transformaciones solo se define cuando ambas transformaciones tienen el mismo dominio y codominio. - Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) ser una transformación, y dejar\(c\) que sea un escalar. El producto escalar de\(c\) con\(T\) es la transformación\(cT\colon\mathbb{R}^n \to\mathbb{R}^m \) definida por
\[(cT)(x)=c\cdot T(x).\nonumber\]
Para enfatizar, la suma de dos transformaciones\(T,U\colon\mathbb{R}^n \to\mathbb{R}^m \) es otra transformación llamada\(T+U\text{;}\) su valor en un vector de entrada\(x\) es la suma de las salidas de\(T\) y\(U\). De igual manera, el producto de\(T\) con un escalar\(c\) es otra transformación llamada\(cT\text{;}\) su valor en un vector de entrada\(x\) es el vector\(c\cdot T(x)\).
Definir\(f\colon \mathbb{R} \to\mathbb{R} \) por\(f(x) = x^2\) y\(g\colon \mathbb{R} \to\mathbb{R} \) por\(g(x) = x^3\). La suma\(f+g\colon \mathbb{R} \to\mathbb{R} \) es la transformación definida por la regla
\[ (f+g)(x) = f(x) + g(x) = x^2 + x^3. \nonumber \]
Por ejemplo,\((f+g)(-2) = (-2)^2 + (-2)^3 = -4\).
Definir\(\exp\colon \mathbb{R} \to\mathbb{R} \) por\(\exp(x) = e^x\). El producto\(2\exp\colon \mathbb{R} \to\mathbb{R} \) es la transformación definida por la regla
\[ (2\exp)(x) = 2\cdot\exp(x) = 2e^x. \nonumber \]
Por ejemplo,\((2\exp)(1) = 2\cdot\exp(1) = 2e\).
\(S,T,U\colon\mathbb{R}^n \to\mathbb{R}^m \)Dejen ser transformaciones y dejar que\(c,d\) sean escalares. Las siguientes propiedades son fácilmente verificadas:
\ begin {alinear*} T + U\ amp= U + T\ amp S + (T + U)\ amp= (S + T) + U\\ c (T + U)\ amp= cT + cU\ amp (c + d) T\ amp= cT + dT\\ c (dT)\ amp= (cd) T\ amp T + 0\ amp= T\ end {alinear*}
En una de las propiedades anteriores, se utilizó\(0\) para denotar la transformación\(\mathbb{R}^n \to\mathbb{R}^m \) que es cero en cada vector de entrada:\(0(x) = 0\) para todos\(x\). A esto se le llama la transformación cero.
Ahora damos las operaciones análogas para matrices.
- La suma de dos\(m\times n\) matrices es la matriz obtenida sumando las entradas de\(A\) e\(B\) individualmente:
\[\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13} \\ a_{21}&a_{22}&a_{23}\end{array}\right)+\left(\begin{array}{ccc}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\end{array}\right)=\left(\begin{array}{ccc}a_{11}+b_{11}&a_{12}+b_{12}&a_{13}+b_{13} \\ a_{21}+b_{21}&a_{22}+b_{22}&a_{23}+b_{23}\end{array}\right)\nonumber\]
En otras palabras, la\(i,j\) entrada de\(A+B\) es la suma de las\(i,j\) entradas de\(A\) y\(B\). Tenga en cuenta que la adición de matrices solo se define cuando ambas matrices tienen el mismo tamaño. - El producto escalar de un escalar\(c\) con una matriz\(A\) se obtiene escalando todas las entradas de\(A\) por\(c\text{:}\)
\[\color{red}{c}\color{black}{\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\end{array}\right)=}\left(\begin{array}{ccc}\color{red}{c}\color{black}{a_{11}}&\color{red}{a}\color{black}{a_{12}}&\color{red}{c}\color{black}{a_{13}} \\ \color{red}{c}\color{black}{a_{21}}&\color{red}{c}\color{black}{a_{22}}&\color{red}{c}\color{black}{a_{23}}\end{array}\right)\nonumber\]
En otras palabras, la\(i,j\) entrada de\(cA\) es\(c\) veces la\(i,j\) entrada de \(A\).
Dejar\(T,U\colon\mathbb{R}^n \to\mathbb{R}^m \) ser transformaciones lineales con matrices estándar\(A,B\text{,}\) respectivamente, y dejar\(c\) ser un escalar.
- La matriz estándar para\(T+U\) es\(A+B\).
- La matriz estándar para\(cT\) es\(cA\).
En vista del hecho anterior, las siguientes propiedades, Nota\(\PageIndex{7}\), son consecuencias de las propiedades correspondientes 29 de transformaciones. También se verifican fácilmente directamente a partir de las definiciones.
\(A,B,C\)Dejen ser\(m\times n\) matrices y dejar que\(c,d\) sean escalares. Entonces:
\ begin {align*} A + B\ amp= B + A\ amp C + (A + B)\ amp= (C + A) + B\\ c (A + B)\ amp= cA + cB\ amp (c + d) A\ amp= cA + dA\\ c (dA)\ amp= (cd) A\ amp A + 0\ amp= A\ end {align*}
En una de las propiedades anteriores, se utilizó\(0\) para denotar la\(m\times n\) matriz cuyas entradas son todas cero. Esta es la matriz estándar de la transformación cero, y se llama la matriz cero.
También podemos combinar adición y multiplicación escalar de matrices con multiplicación de matrices. Dado que la multiplicación matricial corresponde a la composición de las transformaciones (Teorema\(\PageIndex{1}\)), las siguientes propiedades son consecuencias de las propiedades correspondientes, Nota\(\PageIndex{2}\) de transformaciones.
Dejar\(A,B,C\) ser matrices y dejar\(c\) ser un escalar. Supongamos que\(A\) es una\(m\times n\) matriz, y que en cada una de las siguientes identidades, los tamaños de\(B\) y\(C\) son compatibles cuando sea necesario para que se defina el producto. Entonces:
\ begin {alinear*} C (A+B)\ amp= C A+C B\ amp (A + B) C\ amp= A C + B C\ amp\ amp\ c (A B)\ amp= (cA) B\ amp c (A B)\ amp= A (cB)\ A i_n\ amp= A\ amp I_m A\ amp= A\ amp = A\ (A B) C\ amp= A (BC)\ amp\ final {alinear*}
La mayoría de las propiedades anteriores se verifican fácilmente directamente a partir de las definiciones. La propiedad de asociatividad\((AB)C=A(BC)\text{,}\) sin embargo, no lo es (¡pruébalo!). Es mucho más fácil de probar relacionando la multiplicación matricial con la composición de las transformaciones, y utilizando el hecho obvio de que la composición de las transformaciones es asociativa.


