3.5: Inversión de matriz
- Page ID
- 113079
- Entender lo que significa que una matriz cuadrada sea invertible.
- Conozca las transformaciones invertibles y comprenda la relación entre matrices invertibles y transformaciones invertibles.
- Recetas: computar la matriz inversa, resolver un sistema lineal tomando inversas.
- Imagen: la inversa de una transformación.
- Palabras de vocabulario: matriz inversa, transformación inversa.
En la Sección 3.1 aprendimos a multiplicar matrices juntas. En esta sección aprendemos a “dividir” por una matriz. Esto nos permite resolver la ecuación matricial\(Ax=b\) de una manera elegante:
\[ Ax = b \quad\iff\quad x = A^{-1} b. \nonumber \]
Uno tiene que tener cuidado al “dividir por matrices”, sin embargo, porque no todas las matrices tienen una inversa, y el orden de multiplicación matricial es importante.
Matrices Invertibles
El recíproco o inverso de un número distinto de cero\(a\) es el número\(b\) que se caracteriza por la propiedad que\(ab = 1\). Por ejemplo, la inversa de\(7\) es\(1/7\). Utilizamos esta formulación para definir la inversa de una matriz.
Dejar\(A\) ser una matriz\(n\times n\) (cuadrada). Decimos que\(A\) es invertible si hay una\(n\times n\) matriz\(B\) tal que
\[ AB = I_n \quad\text{and}\quad BA = I_n. \nonumber \]
En este caso, la matriz\(B\) se llama la inversa de\(A\text{,}\) y escribimos\(B = A^{-1}\).
Tenemos que exigir\(AB = I_n\) y\(BA = I_n\) porque en general la multiplicación matricial no es conmutativa. No obstante, mostraremos en el Corolario 3.6.1 en la Sección 3.6 que si\(A\) y\(B\) son\(n\times n\) matrices tales que\(AB = I_n\text{,}\) entonces automáticamente\(BA = I_n\).
Verificar que las matrices
\[A=\left(\begin{array}{cc}2&1\\1&1\end{array}\right)\quad\text{and}\quad B=\left(\begin{array}{cc}1&-1\\-1&2\end{array}\right)\nonumber\]
son inversos.
Solución
Vamos a comprobar eso\(AB = I_2\) y aquello\(BA = I_2\).
\[\begin{aligned}AB&=\left(\begin{array}{cc}2&1\\1&1\end{array}\right)\left(\begin{array}{cc}1&-1\\-1&2\end{array}\right)=\left(\begin{array}{cc}1&0\\0&1\end{array}\right) \\ BA&=\left(\begin{array}{cc}1&-1\\-1&2\end{array}\right)\left(\begin{array}{cc}2&1\\1&1\end{array}\right)=\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\end{aligned}\]
Por lo tanto,\(A\) es invertible, con inversa\(B\).
Existen matrices no cuadradas cuyo producto es la identidad. En efecto, si
\[A=\left(\begin{array}{ccc}1&0&0\\0&1&0\end{array}\right)\quad\text{and}\quad B=\left(\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right)\nonumber\]
entonces\(AB = I_2.\) Sin embargo,\(BA\neq I_3\text{,}\) así\(B\) no merece ser llamado el inverso de\(A\).
Se puede mostrar usando las ideas más adelante en esta sección que si\(A\) es una\(n\times m\) matriz para\(n\neq m\text{,}\) entonces no hay una\(m\times n\) matriz\(B\) tal que\(AB = I_m\) y\(BA = I_n\). Por esta razón, nos limitamos a matrices cuadradas cuando discutimos la invertibilidad matricial.
Dejar\(A\) y\(B\) ser\(n\times n\) matrices invertibles.
- \(A^{-1}\)es invertible, y su inversa es\((A^{-1}){}^{-1} = A.\)
- \(AB\)es invertible, y su inverso es\((AB)^{-1} = B^{-1} A^{-1}\) (tenga en cuenta el orden).
- Prueba
-
- Las ecuaciones\(AA^{-1}=I_n\) y\(A^{-1}A = I_n\) al mismo tiempo exhiben\(A^{-1}\) como la inversa de\(A\) y\(A\) como la inversa de\(A^{-1}.\)
- Calculamos
\[ (B^{-1} A^{-1})AB = B^{-1}(A^{-1} A)B = B^{-1} I_n B = B^{-1} B = I_n. \nonumber \]
Aquí se utilizó la asociatividad de la multiplicación matricial y el hecho de que\(I_n B = B\). Esto demuestra que\(B^{-1} A^{-1}\) es lo inverso de\(AB\).
¿Por qué es lo inverso de\(AB\) no igual a\(A^{-1} B^{-1}\text{?}\) Si lo fuera, entonces habríamos
\[ I_n = (AB)(A^{-1} B^{-1}) = ABA^{-1} B^{-1}. \nonumber \]
Pero no hay razón para\(ABA^{-1} B^{-1}\) igualar la matriz de identidad: no se puede cambiar el orden de\(A^{-1}\) y\(B\text{,}\) entonces no hay nada que cancelar en esta expresión. De hecho, si\(I_n = (AB)(A^{-1} B^{-1})\text{,}\) entonces podemos multiplicar ambos lados de la derecha por\(BA\) para concluir eso\(AB = BA\). En otras palabras,\((AB)^{-1} = A^{-1} B^{-1}\) si y sólo si\(AB=BA\).
De manera más general, la inversa de un producto de varias matrices invertibles es el producto de las inversas, en el orden opuesto; la prueba es la misma. Por ejemplo,
\[ (ABC)^{-1} = C^{-1} B^{-1} A^{-1}. \nonumber \]
Computación de la matriz inversa
Hasta el momento hemos definido la matriz inversa sin dar ninguna estrategia para computarla. Lo hacemos ahora, comenzando por el caso especial de\(2\times 2\) las matrices. Entonces le daremos una receta para el\(n\times n\) caso.
El determinante de una\(2\times 2\) matriz es el número
\[\text{det}\left(\begin{array}{cc}a&b\\c&d\end{array}\right)=ad-bc.\nonumber\]
Vamos\(A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\).
- Si\(\det(A) \neq 0\text{,}\) entonces\(A\) es invertible, y
\[ A^{-1} = \frac 1{\det(A)}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right). \nonumber \] - Si\(\det(A) = 0,\) entonces no\(A\) es invertible.
- Prueba
-
- Supongamos que\(\det(A)\neq 0\). Definir\(\displaystyle B = \frac 1{\det(A)}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right).\) Entonces
\[ AB = \left(\begin{array}{cc}a&b\\c&d\end{array}\right) \frac 1{\det(A)}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right) = \frac 1{ad-bc}\left(\begin{array}{cc}ad-bc&0\\0&ad-bc\end{array}\right) = I_2. \nonumber \]
El lector puede comprobar que\(BA = I_2\text{,}\) así\(A\) es invertible y\(B = A^{-1}\). - Supongamos que\(\det(A) = ad-bc = 0\). \(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \)Sea la transformación matricial\(T(x) = Ax\). Entonces
\[\begin{aligned}T\left(\begin{array}{c}-b\\a\end{array}\right)&=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{c}-b\\a\end{array}\right)=\left(\begin{array}{cc}-ab+ab\\-bc+ad\end{array}\right)=\left(\begin{array}{c}0\\ \det(A)\end{array}\right)=0 \\ T\left(\begin{array}{c}d\\-c\end{array}\right)&=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{c}d\\-c\end{array}\right)=\left(\begin{array}{c}ad-bc\\cd-cd\end{array}\right)=\left(\begin{array}{c}\det(A)\\0\end{array}\right)=0.\end{aligned}\]
Si\(A\) es la matriz cero, entonces obviamente no es invertible. De lo contrario, uno de\(v= {-b\choose a}\) y\(v = {d\choose -c}\) será un vector distinto de cero en el espacio nulo de\(A\). Supongamos que había una matriz\(B\) tal que\(BA=I_2\). Entonces
\[ v = I_2v = BAv = B0 = 0, \nonumber \]
que es imposible como\(v\neq 0\). Por lo tanto, no\(A\) es invertible.
- Supongamos que\(\det(A)\neq 0\). Definir\(\displaystyle B = \frac 1{\det(A)}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right).\) Entonces
Existe una fórmula análoga para la inversa de una\(n\times n\) matriz, pero no es tan simple, y es computacionalmente intensiva. El lector interesado lo puede encontrar en la Subsección Regla de Cramer y Matriz Inversa en la Sección 4.2.
Let
\[ A = \left(\begin{array}{cc}1&2\\3&4\end{array}\right). \nonumber \]
Entonces\(\det(A) = 1\cdot 4 - 2\cdot 3 = -2.\) por la Proposición\(\PageIndex{1}\), la matriz\(A\) es invertible con inversa
\[\left(\begin{array}{cc}1&2\\3&4\end{array}\right)^{-1}=\frac{1}{\det(A)}\left(\begin{array}{cc}4&-2\\-3&1\end{array}\right)=-\frac{1}{2}\left(\begin{array}{cc}4&-2\\-3&1\end{array}\right).\nonumber\]
Verificamos:
\[\left(\begin{array}{cc}1&2\\3&4\end{array}\right)\cdot -\frac{1}{2}\left(\begin{array}{cc}4&-2\\-3&1\end{array}\right)=-\frac{1}{2}\left(\begin{array}{cc}-2&0\\0&-2\end{array}\right)=I_2.\nonumber\]
El siguiente teorema da un procedimiento para la computación\(A^{-1}\) en general.
Dejar\(A\) ser una\(n\times n\) matriz, y dejar\((\,A\mid I_n\,)\) ser la matriz obtenida al aumentar\(A\) por la matriz de identidad. Si la forma escalón de fila reducida de\((\,A\mid I_n\,)\) tiene la forma\((\,I_n\mid B\,)\text{,}\) entonces\(A\) es invertible y\(B = A^{-1}\). De lo contrario, no\(A\) es invertible.
- Prueba
-
Primero supongamos que la forma escalón de fila reducida de\((\,A\mid I_n\,)\) no tiene la forma\((\,I_n\mid B\,)\). Esto significa que menos de\(n\) pivotes están contenidos en las primeras\(n\) columnas (la parte no aumentada), por lo que\(A\) tiene menos que\(n\) pivotes. De ello se deduce que\(\text{Nul}(A)\neq\{0\}\) (la ecuación\(Ax=0\) tiene una variable libre), por lo que existe un vector distinto de cero\(v\) en\(\text{Nul}(A)\). Supongamos que había una matriz\(B\) tal que\(BA=I_n\). Entonces
\[ v = I_nv = BAv = B0 = 0, \nonumber \]
lo cual es imposible como\(v\neq 0\). Por lo tanto, no\(A\) es invertible.
Ahora supongamos que la forma escalón de fila reducida de\((\,A\mid I_n\,)\) tiene la forma\((\,I_n\mid B\,)\). En este caso, todos los pivotes están contenidos en la parte no aumentada de la matriz, por lo que la parte aumentada no juega ningún papel en la reducción de filas: las entradas de la parte aumentada no influyen en la elección de las operaciones de fila utilizadas. Por lo tanto, la reducción de filas\((\,A\mid I_n\,)\) equivale a resolver los\(n\) sistemas de ecuaciones lineales\(Ax_1 = e_1,\,Ax_2=e_2,\,\ldots,Ax_n=e_n\text{,}\) donde\(e_1,e_2,\ldots,e_n\) están los vectores de coordenadas estándar, Nota 3.3.2 en la Sección 3.3:
\[\begin{aligned} Ax_1=\color{blue}{e_1}\color{black}{:}\quad &\left(\begin{array}{ccc|ccc}1&0&4&\color{blue}{1}&\color{gray}{0}&\color{gray}{0} \\ 0&1&2&\color{blue}{0}&\color{gray}{1}&\color{gray}{0} \\ 0&-3&-4&\color{blue}{0}&\color{gray}{0}&\color{gray}{1}\end{array}\right) \\ Ax_2=\color{red}{e_2}\color{black}{:}\quad &\left(\begin{array}{ccc|ccc}1&0&4&\color{gray}{1}&\color{red}{0}&\color{gray}{0}\\0&1&2&\color{gray}{0}&\color{red}{1}&\color{gray}{0} \\ 0&-3&-4&\color{gray}{0}&\color{red}{0}&\color{gray}{1}\end{array}\right) \\ Ax_3=\color{Green}{e_3}\color{black}{:}\quad &\left(\begin{array}{ccc|ccc}1&0&4&\color{gray}{1}&\color{gray}{0}&\color{Green}{0}\\0&1&2&\color{gray}{0}&\color{gray}{1}&\color{Green}{0}\\0&-3&-4&\color{gray}{0}&\color{gray}{0}&\color{Green}{1}\end{array}\right).\end{aligned}\]
Las columnas\(x_1,x_2,\ldots,x_n\) de la matriz\(B\) en la forma de fila reducida son las soluciones a estas ecuaciones:
\[\begin{aligned} A\color{blue}{\left(\begin{array}{c}1\\0\\0\end{array}\right)}\color{black}{=e_1:}\quad &\left(\begin{array}{ccc|ccc}1&0&0&\color{blue}{1}&\color{gray}{-6}&\color{gray}{-2} \\ 0&1&0&\color{blue}{0}&\color{gray}{-2}&\color{gray}{-1}\\ 0&0&1&\color{blue}{0}&\color{gray}{3/2}&\color{gray}{1/2}\end{array}\right) \\ A\color{red}{\left(\begin{array}{c}-6\\-2\\3/2\end{array}\right)}\color{black}{=e_2:}\quad &\left(\begin{array}{ccc|ccc}1&0&0&\color{gray}{1}&\color{red}{-6}&\color{gray}{-2}\\0&1&0&\color{gray}{0}&\color{red}{-2}&\color{gray}{-1}\\ 0&0&1&\color{gray}{0}&\color{red}{3/2}&\color{gray}{1/2}\end{array}\right) \\ A\color{Green}{\left(\begin{array}{c}-2\\-1\\1/2\end{array}\right)}\color{black}{=e_3:}\quad &\left(\begin{array}{ccc|ccc}1&0&0&\color{gray}{1}&\color{gray}{-6}&\color{Green}{-2}\\ 0&1&0&\color{gray}{0}&\color{gray}{-2}&\color{Green}{-1}\\ 0&0&1&\color{gray}{0}&\color{gray}{3/2}&\color{Green}{1/2}\end{array}\right).\end{aligned}\]
Por Hecho 3.3.2 en la Sección 3.3, el producto\(Be_i\) es solo la columna\(i\) th\(x_i\) de\(B\text{,}\) tan
\[ e_i = Ax_i = ABe_i \nonumber \]
para todos\(i\). Por el mismo hecho, la columna\(i\) th de\(AB\) es\(e_i\text{,}\) lo que significa que\(AB\) es la matriz de identidad. Así\(B\) es la inversa de\(A\).
Encuentra la inversa de la matriz
\[ A = \left(\begin{array}{ccc}1&0&4\\0&1&2\\0&-3&-4\end{array}\right). \nonumber \]
Solución
Aumentamos por la identidad y la fila reducimos:
\[\begin{aligned}\left(\begin{array}{ccc|ccc}1&0&4&1&0&0\\0&1&2&0&1&0\\0&-3&-4&0&0&1\end{array}\right) \quad\xrightarrow{R_3=R_3+3R_2}\quad &\left(\begin{array}{ccc|ccc}1&0&4&1&0&0\\0&1&2&0&1&0\\0&\color{red}{0}&\color{red}{2}&\color{black}{0}&\color{red}{3}&\color{black}{1}\end{array}\right) \\ {}\xrightarrow{\begin{array}{l}{R_1=R_1-2R_3}\\{R_2=R_2-R_3}\end{array}}\quad &\left(\begin{array}{ccc|ccc}1&0&\color{red}{0}&\color{black}{1}&\color{red}{-6}&\color{red}{-2} \\ 0&1&\color{red}{0}&\color{black}{0}&\color{red}{-2}&\color{red}{-1} \\ 0&0&2&0&3&1\end{array}\right) \\ {}\xrightarrow{R_3=R_3\div 2}\quad &\left(\begin{array}{ccc|ccc}1&0&0&1&-6&-2 \\ 0&1&0&0&-2&-1 \\ 0&0&\color{red}{1}&\color{black}{0}&\color{red}{3/2}&\color{red}{1/2}\end{array}\right).\end{aligned}\]
Por el Teorema\(\PageIndex{1}\), la matriz inversa es
\[\left(\begin{array}{ccc}1&0&4\\0&1&2\\0&-3&-4\end{array}\right)^{-1}=\left(\begin{array}{ccc}1&-6&-2\\0&-2&-1\\0&3/2&1/2\end{array}\right).\nonumber\]
Verificamos:
\[\left(\begin{array}{ccc}1&0&4\\0&1&2\\0&-3&-4\end{array}\right)\left(\begin{array}{ccc}1&-6&-2\\0&-2&-1\\0&3/2&1/2\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right).\nonumber\]
¿La siguiente matriz es invertible?
\[A=\left(\begin{array}{ccc}1&0&4\\0&1&2\\0&-3&-6\end{array}\right).\nonumber\]
Solución
Aumentamos por la identidad y la fila reducimos:
\[\left(\begin{array}{ccc|ccc}1&0&4&1&0&0\\0&1&2&0&1&0\\0&-3&-6&0&0&1\end{array}\right)\quad\xrightarrow{R_3=R_3+3R_2}\quad\left(\begin{array}{ccc|ccc}1&0&4&1&0&0\\0&1&2&0&1&0\\0&\color{red}{0}&\color{red}{0}&\color{black}{0}&\color{black}{3}&\color{black}{1}\end{array}\right).\nonumber\]
En este punto podemos detenernos, porque está claro que la forma de escalón de fila reducida no tendrá\(I_3\) en la parte no aumentada: tendrá una fila de ceros. Por el Teorema\(\PageIndex{1}\), la matriz no es invertible.
Resolver sistemas lineales usando inversos
En esta subsección, aprendemos a resolver\(Ax=b\) “dividiendo por”\(A\).
Dejar\(A\) ser una\(n\times n\) matriz invertible, y dejar\(b\) ser un vector en\(\mathbb{R}^n .\) Entonces la ecuación matricial\(Ax=b\) tiene exactamente una solución:
\[ x = A^{-1} b. \nonumber \]
- Prueba
-
Calculamos:
\[ \begin{split} Ax = b \quad\implies\amp\quad A^{-1}(Ax) = A^{-1} b \\ \quad\implies\amp\quad (A^{-1} A)x = A^{-1} b \\ \quad\implies\amp\quad I_n x = A^{-1} b \\ \quad\implies\amp\quad x = A^{-1} b. \end{split} \nonumber \]
Aquí se utilizó la asociatividad de la multiplicación matricial, y el hecho de que\(I_n x = x\) para cualquier vector\(b\).
Resolver la ecuación matricial
\[ \left(\begin{array}{cc}1&3\\-1&2\end{array}\right)x = \left(\begin{array}{c}1\\1\end{array}\right). \nonumber \]
Solución
Por el Teorema\(\PageIndex{2}\), la única solución de nuestro sistema lineal es
\[x=\left(\begin{array}{cc}1&3\\-1&2\end{array}\right)^{-1}\left(\begin{array}{c}1\\1\end{array}\right)=\frac{1}{5}\left(\begin{array}{cc}2&-3\\1&1\end{array}\right)\left(\begin{array}{c}1\\1\end{array}\right)=\frac{1}{5}\left(\begin{array}{c}-1\\2\end{array}\right).\nonumber\]
Aquí usamos
\[\det\left(\begin{array}{cc}1&3\\-1&2\end{array}\right)=1\cdot 2-(-1)\cdot 3=5.\nonumber\]
Resolver el sistema de ecuaciones
\[\left\{\begin{array}{rrrrrrl} 2x_1 &+& 3x_2 &+& 2x_3 &=& 1\\ x_1 &{}&{}& + &3x_3 &=& 1\\ 2x_1 &+& 2x_2 &+& 3x_3 &=& 1.\end{array}\right.\nonumber\]
Solución
Primero escribimos nuestro sistema como una ecuación matricial\(Ax = b\text{,}\) donde
\[A=\left(\begin{array}{ccc}2&3&2\\1&0&3\\2&2&3\end{array}\right)\quad\text{and}\quad b=\left(\begin{array}{c}1\\1\\1\end{array}\right).\nonumber\]
A continuación encontramos la inversa de\(A\) por aumento y reducción de filas:
\[\begin{aligned}\left(\begin{array}{ccc|ccc}2&3&2&1&0&0\\1&0&3&0&1&0\\2&2&3&0&0&1\end{array}\right)\quad\xrightarrow{R_1\leftrightarrow R_2}\quad &\left(\begin{array}{ccc|ccc}\color{red}{1}&\color{black}{0}&3&0&1&0\\2&3&2&1&0&0\\2&2&3&0&0&1\end{array}\right) \\ {}\xrightarrow{\begin{array}{l}{R_2=R_2-2R_1}\\{R_3=R_3-2R_1}\end{array}}\quad &\left(\begin{array}{ccc|ccc}1&0&3&0&1&0\\ \color{red}{0}&\color{black}{3}&-4&1&-2&0 \\ \color{red}{0}&\color{black}{2}&-3&0&-2&1\end{array}\right) \\ {}\xrightarrow{R_2=R_2-R_3}\quad &\left(\begin{array}{ccc|ccc}1&0&3&0&1&0\\0&\color{red}{1}&\color{black}{-1}&1&0&-1\\0&2&-3&0&-2&1\end{array}\right) \\ {}\xrightarrow{R_3=R_3-2R_2}\quad &\left(\begin{array}{ccc|ccc}1&0&3&0&1&0\\0&1&-1&1&0&-1 \\ 0&\color{red}{0}&-1&-2&-2&3\end{array}\right) \\ {}\xrightarrow{R_3=-R_3}\quad &\left(\begin{array}{ccc|ccc}1&0&3&0&1&0\\0&1&-1&1&0&-1\\0&0&\color{red}{1}&\color{black}{2}&2&-3\end{array}\right) \\ {}\xrightarrow{\begin{array}{l}{R_1=R_1-3R_3}\\{R_2=R_2+R_3}\end{array}}\quad &\left(\begin{array}{ccc|ccc}1&0&\color{red}{0}&\color{black}{-6}&-5&9\\ 0&1&\color{red}{0}&\color{black}{3}&2&-4 \\ 0&0&1&2&2&-3\end{array}\right).\end{aligned}\]
Por el Teorema\(\PageIndex{2}\), la única solución de nuestro sistema lineal es
\[\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{ccc}2&3&2\\1&0&3\\2&2&3\end{array}\right)^{-1}\left(\begin{array}{c}1\\1\\1\end{array}\right)=\left(\begin{array}{ccc}-6&-5&9\\3&2&-4\\2&2&-3\end{array}\right)\left(\begin{array}{c}1\\1\\1\end{array}\right)=\left(\begin{array}{c}-2\\1\\1\end{array}\right).\nonumber\]
La ventaja de resolver un sistema lineal usando inversas es que se vuelve mucho más rápido resolver la ecuación matricial\(Ax=b\) para otros, o incluso desconocidos, valores de\(b\). Por ejemplo, en el ejemplo anterior, la solución del sistema de ecuaciones
\[\left\{\begin{array}{rrrrrrl}2x_1 &+& 3x_2 &+& 2x_3 &=& b_1\\ x_1 &{}&{}& + &3x_3 &=& b_2\\ 2x_1 &+& 2x_2 &+& 3x_3 &=& b_3,\end{array}\right.,\nonumber\]
donde\(b_1,b_2,b_3\) están las incógnitas, es
\[\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{ccc}2&3&2\\1&0&3\\2&2&3\end{array}\right)^{-1}\left(\begin{array}{c}b_1\\b_2\\b_3\end{array}\right)=\left(\begin{array}{ccc}-6&-5&9\\3&2&-4\\2&2&-3\end{array}\right)\left(\begin{array}{c}b_1\\b_2\\b_3\end{array}\right)=\left(\begin{array}{r}-6b_1-5b_2+9b_3 \\ 3b_1+2b_2-4b_3 \\ 2b_1+2b_2-3b_3\end{array}\right).\nonumber\]
Transformaciones lineales invertibles
Al igual que con la multiplicación matricial, es útil entender la inversión matricial como una operación sobre transformaciones lineales. Recordemos que se denota la transformación de identidad, Definición 3.1.2 en la Sección 3.1, on\(\mathbb{R}^n \)\(\text{Id}_{\mathbb{R}^n }\).
Una transformación\(T\colon\mathbb{R}^n \to\mathbb{R}^n \) es invertible si existe una transformación\(U\colon\mathbb{R}^n \to\mathbb{R}^n \) tal que\(T\circ U = \text{Id}_{\mathbb{R}^n }\) y\(U\circ T = \text{Id}_{\mathbb{R}^n }\). En este caso, la transformación\(U\) se llama la inversa de\(T\text{,}\) y escribimos\(U = T^{-1}\).
El inverso\(U\) de\(T\) “deshace” lo que sea que haya\(T\) hecho. Tenemos
\[ T\circ U(x) = x \quad\text{and}\quad U\circ T(x) = x \nonumber \]
para todos los vectores\(x\). Esto significa que si aplicas\(T\) a\(x\text{,}\) entonces aplicas\(U\text{,}\) obtienes el vector de\(x\) vuelta, y de igual manera en el otro orden.
Definir\(f\colon \mathbb{R} \to\mathbb{R} \) por\(f(x) = 2x\). Se trata de una transformación invertible, con inversa\(g(x) = x/2\). En efecto,
\[ f\circ g(x) = f(g(x)) = f\biggl(\frac x2\biggr) = 2\biggl(\frac x2\biggr) = x \nonumber \]
y
\[ g\circ f(x) = g(f(x)) = g(2x) = \frac{2x}2 = x. \nonumber \]
En otras palabras, dividir por\(2\) deshace la transformación que se multiplica por\(2\).
Definir\(f\colon \mathbb{R} \to\mathbb{R} \) por\(f(x) = x^3\). Se trata de una transformación invertible, con inversa\(g(x) = \sqrt[3]x\). En efecto,
\[ f\circ g(x) = f(g(x)) = f(\sqrt[3]x) = \bigl(\sqrt[3]x\bigr)^3 = x \nonumber \]
y
\[ g\circ f(x) = g(f(x)) = g(x^3) = \sqrt[3]{x^3} = x. \nonumber \]
En otras palabras, tomar la raíz cubo deshace la transformación que lleva un número a su cubo.
Definir\(f\colon \mathbb{R} \to\mathbb{R} \) por\(f(x) = x^2\). Esta no es una función invertible. En efecto, tenemos\(f(2) = 2 = f(-2)\text{,}\) así que no hay manera de deshacer\(f\text{:}\) la transformación inversa no sabría si debería enviar\(2\) a\(2\) o\(-2\). Más formalmente, si\(g\colon \mathbb{R} \to\mathbb{R} \) satisface\(g(f(x)) = x\text{,}\) entonces
\[ 2 = g(f(2)) = g(2) \quad\text{and}\quad -2 = g(f(-2)) = g(2), \nonumber \]
lo cual es imposible:\(g(2)\) es un número, por lo que no puede ser igual\(2\) y\(-2\) al mismo tiempo.
Definir\(f\colon \mathbb{R} \to\mathbb{R} \) por\(f(x) = e^x\). Esta no es una función invertible. En efecto, si hubiera una función\(g\colon \mathbb{R} \to\mathbb{R} \) tal que\(f\circ g = \text{Id}_{\mathbb{R}}\text{,}\) entonces tendríamos
\[ -1 = f\circ g(-1) = f(g(-1)) = e^{g(-1)}. \nonumber \]
Pero\(e^x\) es un número positivo para cada\(x\text{,}\) así que esto es imposible.
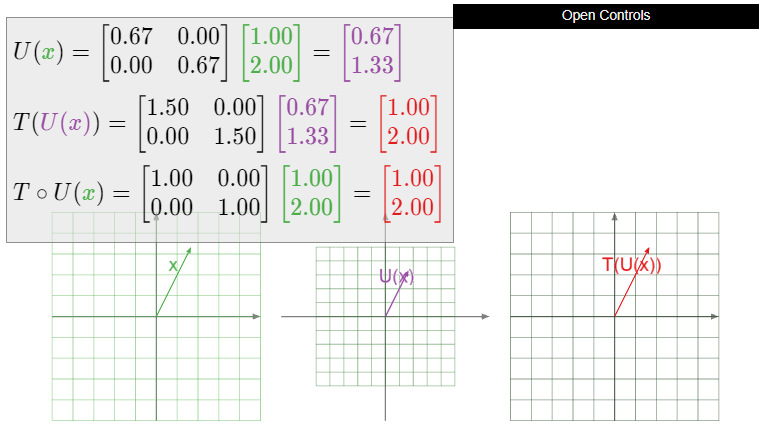
Dejar\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser la dilatación por un factor de\(3/2\text{:}\) eso es,\(T(x) = 3/2x\). ¿Es\(T\) invertible? Si es así, ¿qué es\(T^{-1}\text{?}\)
Solución
Dejar\(U\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser la dilatación por un factor de\(2/3\text{:}\) eso es,\(U(x) = 2/3x\). Entonces
\[ T\circ U(x) = T\biggl(\frac 23x\biggr) = \frac 32\cdot\frac 23x = x \nonumber \]
y
\[ U\circ T(x) = U\biggl(\frac 32x\biggr) = \frac 23\cdot\frac 32x = x. \nonumber \]
De ahí\(T\circ U = \text{Id}_{\mathbb{R}^2 }\) y\(U\circ T = \text{Id}_{\mathbb{R}^2 }\text{,}\) así\(T\) es invertible, con inversa\(U\). Es decir, encogerse por un factor de\(2/3\) deshace estirando por un factor de 3/2.
Figura\(\PageIndex{1}\)
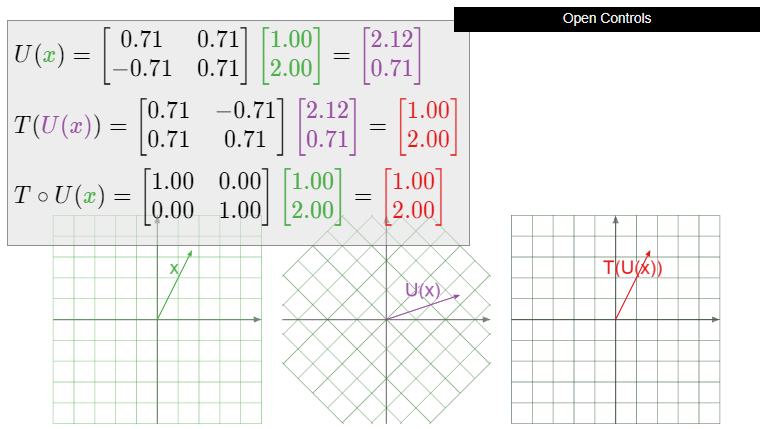
Dejar\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser rotación en sentido antihorario por\(45^\circ\). ¿Es\(T\) invertible? Si es así, ¿qué es\(T^{-1}\text{?}\)
Solución
Dejar\(U\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser rotación en sentido horario por\(45^\circ\). Entonces\(T\circ U\) primero gira en sentido horario\(45^\circ\text{,}\) y luego en sentido contrario a las agujas del reloj por\(45^\circ\text{,}\) lo que la composición gira cero grados: es la transformación de identidad. De igual manera,\(U\circ T\) primero gira en sentido antihorario, luego en sentido horario en la misma cantidad, por lo que es la transformación de identidad. En otras palabras, la rotación en sentido horario\(45^\circ\) deshace la rotación en sentido antihorario por\(45^\circ\).

Figura\(\PageIndex{4}\)
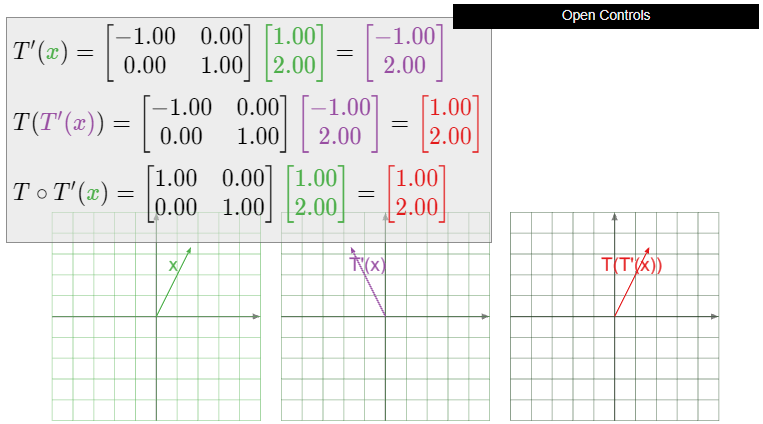
Que\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) sea la reflexión sobre el\(y\) eje -eje. ¿Es\(T\) invertible? Si es así, ¿qué es\(T^{-1}\text{?}\)
Solución
La transformación\(T\) es invertible; de hecho, es igual a su propia inversa. Reflejar un vector\(x\) sobre el\(y\) eje -dos veces lleva el vector de nuevo a donde comenzó, entonces\(T\circ T = \text{Id}_{\mathbb{R}^2 }\).

Figura\(\PageIndex{7}\)
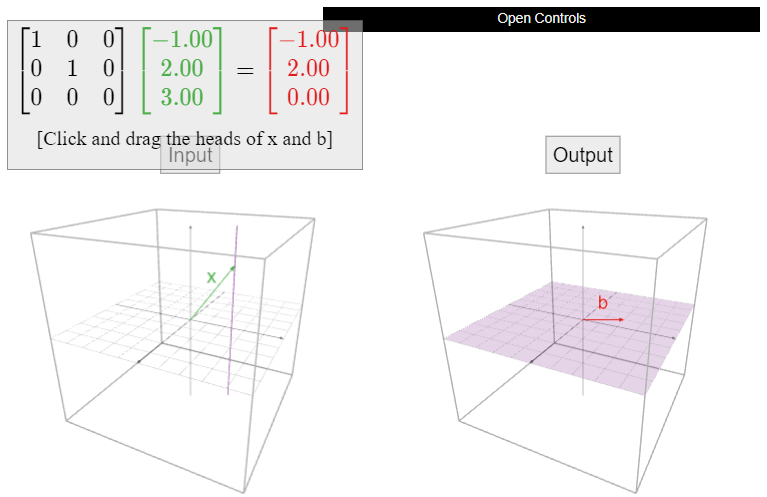
Dejar\(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \) ser la proyección sobre el\(xy\) plano, introducida en el Ejemplo 3.1.3 en la Sección 3.1. ¿Es\(T\) invertible?
Solución
La transformación no\(T\) es invertible. Cada vector en el\(z\) eje -se proyecta sobre el vector cero, por lo que no hay forma de deshacer lo que\(T\) hizo: la transformación inversa no sabría a qué vector en el\(z\) eje debería enviar el vector cero. De manera más formal, supongamos que hubo una transformación\(U\colon\mathbb{R}^3 \to\mathbb{R}^3 \) tal que\(U\circ T = \text{Id}_{\mathbb{R}^3 }\). Entonces
\[ 0 = U\circ T(0) = U(T(0)) = U(0) \nonumber \]
y
\[ \left(\begin{array}{c}0\\0\\1\end{array}\right) = U\circ T\left(\begin{array}{c}0\\0\\1\end{array}\right) = U\left(T\left(\begin{array}{c}0\\0\\1\end{array}\right)\right) = U(0). \nonumber \]
Pero\(U(0)\) es como un solo vector en\(\mathbb{R}^3 \text{,}\) lo que no puede ser igual a\(0\) y\((0, 0, 1)\) a al mismo tiempo.
- Una transformación\(T\colon\mathbb{R}^n \to\mathbb{R}^n \) es invertible si y solo si es tanto uno a uno como a uno.
- Si ya\(T\) se sabe que es invertible, entonces\(U\colon\mathbb{R}^n \to\mathbb{R}^n \) es la inversa de\(T\) siempre que \(U\circ T = \text{Id}_{\mathbb{R}^n }\text{:}\)sea\(T\circ U = \text{Id}_{\mathbb{R}^n }\) o sólo sea necesario verificar uno.
- Prueba
-
Decir que\(T\) es uno a uno y hacia significa que\(T(x)=b\) tiene exactamente una solución para cada\(b\) en\(\mathbb{R}^n \).
Supongamos que\(T\) es invertible. Entonces\(T(x)=b\) siempre tiene la solución única de\(x = T^{-1}(b)\text{:}\) hecho, aplicando\(T^{-1}\) a ambos lados de\(T(x)=b\) da
\[ x = T^{-1}(T(x)) = T^{-1}(b), \nonumber \]
y aplicar\(T\) a ambos lados de\(x = T^{-1}(b)\) da
\[ T(x) = T(T^{-1}(b)) = b. \nonumber \]
Por el contrario, supongamos que\(T\) es uno a uno y sobre. Dejar\(b\) ser un vector en\(\mathbb{R}^n \text{,}\) y dejar\(x = U(b)\) ser la solución única de\(T(x)=b\). Luego\(U\) define una transformación de\(\mathbb{R}^n \) a\(\mathbb{R}^n \). Para cualquiera\(x\) en\(\mathbb{R}^n \text{,}\) lo que tenemos\(U(T(x)) = x\text{,}\) porque\(x\) es la solución única de la ecuación\(T(x) = b\) para\(b = T(x)\). Para cualquiera\(b\) en\(\mathbb{R}^n \text{,}\) lo que tenemos\(T(U(b)) = b\text{,}\) porque\(x = U(b)\) es la solución única de\(T(x)=b\). Por lo tanto,\(U\) es la inversa de\(T\text{,}\) y\(T\) es invertible.
Supongamos ahora que\(T\) es una transformación invertible, y esa\(U\) es otra transformación tal que\(T\circ U = \text{Id}_{\mathbb{R}^n }\). Debemos demostrar eso\(U = T^{-1}\text{,}\) es decir, eso\(U\circ T = \text{Id}_{\mathbb{R}^n }\). Componemos ambos lados de la igualdad\(T\circ U = \text{Id}_{\mathbb{R}^n }\) a la izquierda por\(T^{-1}\) y a la derecha por\(T\) para obtener
\[ T^{-1}\circ T\circ U\circ T = T^{-1}\circ\text{Id}_{\mathbb{R}^n }\circ T. \nonumber \]
Tenemos\(T^{-1}\circ T = \text{Id}_{\mathbb{R}^n }\) y\(\text{Id}_{\mathbb{R}^n }\circ U = U\text{,}\) así lo es el lado izquierdo de la ecuación anterior\(U\circ T\). De igual manera,\(\text{Id}_{\mathbb{R}^n }\circ T = T\) y\(T^{-1}\circ T = \text{Id}_{\mathbb{R}^n }\text{,}\) así nuestra igualdad se simplifica a\(U\circ T = \text{Id}_{\mathbb{R}^n }\text{,}\) lo deseado.
Si en cambio hubiéramos asumido sólo eso\(U\circ T = \text{Id}_{\mathbb{R}^n }\text{,}\) entonces la prueba que\(T\circ U = \text{Id}_{\mathbb{R}^n }\) procede de manera similar.
Tiene sentido en la anterior Definición\(\PageIndex{3}\) definir la inversa de una transformación\(T\colon\mathbb{R}^n \to\mathbb{R}^m \text{,}\)\(m\neq n\text{,}\) para ser una transformación\(U\colon\mathbb{R}^m \to\mathbb{R}^n \) tal que\(T\circ U = \text{Id}_{\mathbb{R}^m }\) y\(U\circ T = \text{Id}_{\mathbb{R}^n }\). De hecho, existen transformaciones invertibles\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) para cualquiera\(m\) y\(n\text{,}\) pero no son lineales, ni siquiera continuas.
Si\(T\) es una transformación lineal, entonces solo puede ser invertible cuando\(m = n\text{,}\) es decir, cuando su dominio es igual a su codominio. En efecto, si\(T\colon\mathbb{R}^n \to\mathbb{R}^m \) es uno a uno, entonces\(n\leq m\) por la Nota 3.2.1 en la Sección 3.2, y si\(T\) está sobre, entonces\(m\leq n\) por la Nota 3.2.2 en la Sección 3.2. Por lo tanto, al discutir la invertibilidad nos limitamos al caso\(m=n\).
Encuentra una transformación invertible (no lineal)\(T\colon\mathbb{R}^2 \to\mathbb{R}\).
Como cabría esperar, la matriz para la inversa de una transformación lineal es la inversa de la matriz para la transformación, como afirma el siguiente teorema.
Dejar\(T\colon\mathbb{R}^n \to\mathbb{R}^n \) ser una transformación lineal con matriz estándar\(A\). Entonces\(T\) es invertible si y sólo si\(A\) es invertible, en cuyo caso\(T^{-1}\) es lineal con matriz estándar\(A^{-1}\).
- Prueba
-
Supongamos que\(T\) es invertible. Dejar\(U\colon\mathbb{R}^n \to\mathbb{R}^n \) ser la inversa de\(T\). Afirmamos que\(U\) es lineal. Necesitamos verificar las propiedades definitorias, Definición 3.3.1, en la Sección 3.3. Dejar\(u,v\) ser vectores en\(\mathbb{R}^n \). Entonces
\[ u + v = T(U(u)) + T(U(v)) = T(U(u) + U(v)) \nonumber \]
por linealidad de\(T\). Aplicar\(U\) a ambos lados da
\[ U(u + v) = U\bigl(T(U(u) + U(v))\bigr) = U(u) + U(v). \nonumber \]
\(c\)Déjese ser un escalar. Entonces
\[ cu = cT(U(u)) = T(cU(u)) \nonumber \]
por linealidad de\(T\). Aplicar\(U\) a ambos lados da
\[ U(cu) = U\bigl(T(cU(u))\bigr) = cU(u). \nonumber \]
Ya que\(U\) satisface las propiedades definitorias, Definición 3.3.1, en la Sección 3.3, es una transformación lineal.
Ahora que sabemos que\(U\) es lineal, sabemos que tiene una matriz estándar\(B\). Por la compatibilidad de la multiplicación matricial y la composición, Teorema 3.4.1 en la Sección 3.4, la matriz para\(T\circ U\) es\(AB\). Pero\(T\circ U\) es la transformación de identidad\(\text{Id}_{\mathbb{R}^n },\) y la matriz estándar para\(\text{Id}_{\mathbb{R}^n }\) es\(I_n\text{,}\) así\(AB = I_n\). Uno muestra de manera similar eso\(BA = I_n\). De ahí\(A\) que sea invertible y\(B = A^{-1}\).
Por el contrario, supongamos que eso\(A\) es invertible. Dejar\(B = A^{-1}\text{,}\) y definir\(U\colon\mathbb{R}^n \to\mathbb{R}^n \) por\(U(x) = Bx\). Por la compatibilidad de la multiplicación matricial y la composición, Teorema 3.4.1 en la Sección 3.4, la matriz para\(T\circ U\) es\(AB = I_n\text{,}\) y la matriz para\(U\circ T\) es\(BA = I_n\). Por lo tanto,
\[ T\circ U(x) = ABx = I_nx = x \quad\text{and}\quad U\circ T(x) = BAx = I_nx = x, \nonumber \]
lo que demuestra que\(T\) es invertible con transformación inversa\(U\).
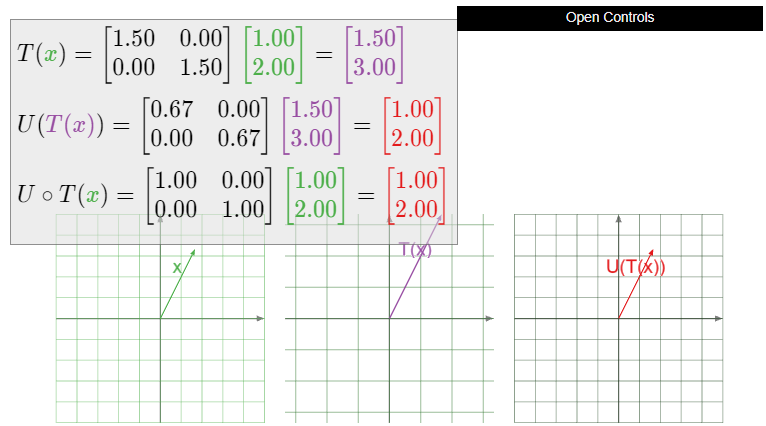
Dejar\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser la dilatación por un factor de\(3/2\text{:}\) eso es,\(T(x) = 3/2x\). ¿Es\(T\) invertible? Si es así, ¿qué es\(T^{-1}\text{?}\)
Solución
En el Ejemplo 3.1.5 en la Sección 3.1 mostramos que la matriz para\(T\) es
\[ A = \left(\begin{array}{cc}3/2&0\\0&3/2\end{array}\right). \nonumber \]
El determinante de\(A\) es\(9/4\neq 0\text{,}\) así\(A\) es invertible con la inversa
\[ A^{-1} = \frac 1{9/4}\left(\begin{array}{cc}3/2&0\\0&3/2\end{array}\right) = \left(\begin{array}{cc}2/3&0\\0&2/3\end{array}\right). \nonumber \]
Por el Teorema\(\PageIndex{3}\),\(T\) es invertible, y su inverso es la transformación matricial para\(A^{-1}\text{:}\)
\[ T^{-1}(x) = \left(\begin{array}{cc}2/3&0\\0&2/3\end{array}\right)x. \nonumber \]
Reconocemos esto como una dilatación por un factor de\(2/3\).
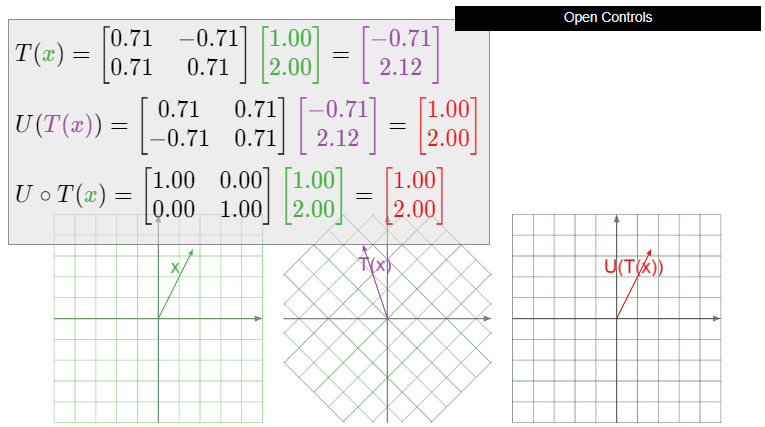
Dejar\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) ser rotación en sentido antihorario por\(45^\circ\). ¿Es\(T\) invertible? Si es así, ¿qué es\(T^{-1}\text{?}\)
Solución
En el Ejemplo 3.3.8 de la Sección 3.3, mostramos que la matriz estándar para la rotación en sentido antihorario del plano por un ángulo de\(\theta\) es
\[ \left(\begin{array}{cc}\cos\theta &-\sin\theta \\ \sin\theta &\cos\theta\end{array}\right). \nonumber \]
Por lo tanto, la matriz estándar\(A\) para\(T\) es
\[ A = \frac 1{\sqrt 2}\left(\begin{array}{cc}1&-1\\1&1\end{array}\right), \nonumber \]
donde hemos utilizado las identidades trigonométricas
\[ \cos(45^\circ) = \frac 1{\sqrt2} \qquad \sin(45^\circ) = \frac 1{\sqrt2}. \nonumber \]
El determinante de\(A\) es
\[ \det(A) = \frac 1{\sqrt2}\cdot\frac 1{\sqrt2} - \frac 1{\sqrt2}\frac{-1}{\sqrt2} = \frac 12 + \frac 12 = 1, \nonumber \]
por lo que la inversa es
\[ A^{-1} = \frac 1{\sqrt2}\left(\begin{array}{cc}1&1\\-1&1\end{array}\right). \nonumber \]
Por el Teorema\(\PageIndex{3}\),\(T\) es invertible, y su inverso es la transformación matricial para\(A^{-1}\text{:}\)
\[ T^{-1}(x) = \frac 1{\sqrt2}\left(\begin{array}{cc}1&1\\-1&1\end{array}\right)x. \nonumber \]
Reconocemos esto como una rotación en sentido horario mediante el\(45^\circ\text{,}\) uso de las identidades trigonométricas
\[ \cos(-45^\circ) = \frac 1{\sqrt2} \qquad \sin(-45^\circ) = -\frac 1{\sqrt2}. \nonumber \]
Que\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) sea la reflexión sobre el\(y\) eje -eje. ¿Es\(T\) invertible? Si es así, ¿qué es\(T^{-1}\text{?}\)
Solución
En el Ejemplo 3.1.4 en la Sección 3.1 mostramos que la matriz para\(T\) es
\[ A = \left(\begin{array}{cc}-1&0\\0&1\end{array}\right). \nonumber \]
Esta matriz tiene determinante\(-1\text{,}\) por lo que es invertible, con
\[ A^{-1} = -\left(\begin{array}{cc}1&0\\0&-1\end{array}\right) = \left(\begin{array}{cc}-1&0\\0&1\end{array}\right) = A. \nonumber \]
Por el Teorema\(\PageIndex{3}\),\(T\) es invertible, y es igual a su propio inverso:\(T^{-1} = T\). Esta es otra forma de decir que una reflexión se “deshace” a sí misma.


