5.4: Diagonalización
- Page ID
- 113122
- Aprender dos criterios principales para que una matriz sea diagonalizable.
- Desarrollar una biblioteca de ejemplos de matrices que sean y no sean diagonalizables.
- Recetas: diagonalizar una matriz, calcular rápidamente los poderes de una matriz por diagonalización.
- Imágenes: la geometría de las matrices diagonales, por qué una cizalla no es diagonalizable.
- Teorema: el teorema de diagonalización (dos variantes).
- Palabras de vocabulario: diagonalizable, multiplicidad algebraica, multiplicidad geométrica.
Las matrices diagonales son el tipo de matrices más fáciles de entender: simplemente escalan las direcciones de coordenadas por sus entradas diagonales. En la Sección 5.3, vimos que matrices similares se comportan de la misma manera, con respecto a diferentes sistemas de coordenadas. Por lo tanto, si una matriz es similar a una matriz diagonal, también es relativamente fácil de entender. Esta sección está dedicada a la pregunta: “¿Cuándo es una matriz similar a una matriz diagonal?” Esta sección está dedicada a la pregunta: “¿Cuándo es una matriz similar a una matriz diagonal?” Veremos que el álgebra y geometría de tal matriz es relativamente fácil de entender.
Diagonalizabilidad
Antes de responder a la pregunta anterior, primero le damos un nombre.
Una\(n\times n\) matriz\(A\) es diagonalizable si es similar a una matriz diagonal: es decir, si existe una\(n\times n\) matriz invertible\(C\) y una matriz diagonal\(D\) tal que
\[ A = CDC^{-1}. \nonumber \]
Cualquier matriz diagonal\(D\) es diagonalizable porque es similar a sí misma, Proposición 5.3.1 en la Sección 5.3. Por ejemplo,
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)=I_{3}\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)I_{3}^{-1}.\nonumber\]
La mayoría de los ejemplos de la Sección 5.3 involucran matrices diagonalizables: Los siguientes son ejemplos de matrices diagonalizables:
\[\begin{array}{lll} \left(\begin{array}{cc}-12&15\\-10&13\end{array}\right)&\begin{array}{l}\text{is diagonalizable} \\ \text{because it equals}\end{array} &\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)\left(\begin{array}{cc}3&0\\0&-2\end{array}\right)\left(\begin{array}{cc}-2&3\\1&-1\end{array}\right)^{-1} \\ \left(\begin{array}{cc}1/2&3/2\\3/2&1/2\end{array}\right)&\begin{array}{l}\text{is diagonalizable} \\ \text{because it equals}\end{array} &\left(\begin{array}{cc}1&1\\1&-1\end{array}\right)\left(\begin{array}{cc}2&0\\0&-1\end{array}\right)\left(\begin{array}{cc}1&1\\1&-1\end{array}\right)^{-1} \\ \frac{1}{5}\left(\begin{array}{cc}-8&-9\\6&13\end{array}\right)&\begin{array}{c}\text{is diagonalizable} \\ \text{because it equals}\end{array}&\frac{1}{2}\left(\begin{array}{cc}-1&-3\\2&1\end{array}\right)\left(\begin{array}{cc}2&0\\0&-1\end{array}\right)\left(\frac{1}{2}\left(\begin{array}{cc}-1&-3\\2&1\end{array}\right)\right)^{-1} \\ \left(\begin{array}{ccc}-1&0&0\\-1&0&2\\-1&1&1\end{array}\right)&\begin{array}{c}\text{is diagonalizable} \\ \text{because it equals}\end{array}&\left(\begin{array}{ccc}-1&1&0\\1&1&1\\-1&0&1\end{array}\right)\left(\begin{array}{ccc}-1&0&0\\0&-1&0\\0&0&2\end{array}\right)\left(\begin{array}{ccc}-1&1&0\\1&1&1\\-1&0&1\end{array}\right)^{-1}.\end{array}\nonumber\]
Si una matriz\(A\) es diagonalizable, y si\(B\) es similar a\(A\text{,}\) entonces\(B\) es diagonalizable también por la Proposición 5.3.1 en la Sección 5.3. también. En efecto, si\(A = CDC^{-1}\) por\(D\) diagonal, y\(B = EAE^{-1}\text{,}\) luego
\[ B = EAE^{-1} = E(CDC^{-1})E^{-1} = (EC)D(EC)^{-1}, \nonumber \]por lo que\(B\) es similar a\(D\).
Poderes de Matrices Diagonalizables
Multiplicar matrices diagonales juntas solo multiplica sus entradas diagonales:
\[\left(\begin{array}{ccc}x_1&0&0\\0&x_2&0\\0&0&x_3\end{array}\right)\left(\begin{array}{ccc}y_1&0&0\\0&y_2&0\\0&0&y_3\end{array}\right)=\left(\begin{array}{ccc}x_1y_1&0&0\\0&x_2y_2&0\\0&0&x_3y_3\end{array}\right).\nonumber\]
Por lo tanto, es fácil tomar potencias de una matriz diagonal:
\[\left(\begin{array}{ccc}x&0&0\\0&y&0\\0&0&z\end{array}\right)^{n}=\left(\begin{array}{ccc}x^n&0&0\\0&y^n&0\\0&0&z^n\end{array}\right).\nonumber\]
Por Hecho 5.3.1 en la Sección 5.3, si\(A = CDC^{-1}\) entonces es\(A^n = CD^nC^{-1}\text{,}\) así también es fácil tomar poderes de matrices diagonalizables. Esto será muy importante en aplicaciones a ecuaciones de diferencia en la Sección 5.6. Esto suele ser muy importante en las aplicaciones.
Si\(A = CDC^{-1}\text{,}\) donde\(D\) es una matriz diagonal, entonces\(A^n = CD^nC^{-1}\text{:}\)
\[A=C\left(\begin{array}{ccc}x&0&0\\0&y&0\\0&0&z\end{array}\right)C^{-1}\quad\implies\quad A^{n}=C\left(\begin{array}{ccc}x^n&0&0\\0&y^n&0\\0&0&z^n\end{array}\right)C^{-1}.\nonumber\]
Let
\[ A = \left(\begin{array}{cc}1/2&3/2\\3/2&1/2\end{array}\right) = \left(\begin{array}{cc}1&1\\1&-1\end{array}\right) \left(\begin{array}{cc}2&0\\0&-1\end{array}\right) \left(\begin{array}{cc}1&1\\1&-1\end{array}\right)^{-1}. \nonumber \]
Encuentra una fórmula para\(A^n\) en la que las entradas son funciones de\(n\text{,}\) donde\(n\) está cualquier número entero positivo.
Solución
Tenemos
\[\begin{aligned}A^n&=\left(\begin{array}{cc}1&1\\1&-1\end{array}\right)\left(\begin{array}{cc}2&0\\0&-1\end{array}\right)^n\left(\begin{array}{cc}1&1\\1&-1\end{array}\right)^{-1} \\ &=\left(\begin{array}{cc}1&1\\1&-1\end{array}\right)\left(\begin{array}{cc}2^n&0 \\ 0&(-1)^n\end{array}\right)\frac{1}{-2}\left(\begin{array}{cc}-1&-1\\-1&1\end{array}\right) \\ &=\left(\begin{array}{cc}2^n &(-1)^n \\ 2^n&(-1)^{n+1}\end{array}\right)\frac{1}{2}\left(\begin{array}{cc}1&1\\1&-1\end{array}\right) \\ &=\frac{1}{2}\left(\begin{array}{cc} 2^n+(-1)^n &2^n +(-1)^{n+1} \\ 2^n +(-1)^{n+1} & 2^n+(-1)^n\end{array}\right),\end{aligned}\]
donde usamos\((-1)^{n+2}=(-1)^2(-1)^n = (-1)^n\).
Una cuestión fundamental sobre una matriz es si es o no diagonalizable. El siguiente es el criterio principal para la diagonalizabilidad. Muestra que la diagonalizabilidad es un problema de valor propio.
Una\(n\times n\) matriz\(A\) es diagonalizable si y solo si\(A\) tiene vectores propios\(n\) linealmente independientes.
En este caso,\(A = CDC^{-1}\) para
\[ C = \left(\begin{array}{cccc}|&|&\quad&| \\ v_1&v_2&\cdots &v_n \\ |&|&\quad &| \end{array}\right) \qquad D = \left(\begin{array}{cccc}\lambda_{1}&0&\cdots &0 \\ 0&\lambda_2&\cdots &0 \\ \vdots &\vdots &\ddots &\vdots \\ 0&0&\cdots&\lambda_{n}\end{array}\right), \nonumber \]
donde\(v_1,v_2,\ldots,v_n\) son vectores propios linealmente independientes, y\(\lambda_1,\lambda_2,\ldots,\lambda_n\) son los valores propios correspondientes, en el mismo orden.
- Prueba
-
Primero supongamos que\(A\) tiene vectores propios\(n\) linealmente independientes\(v_1,v_2,\ldots,v_n\text{,}\) con valores propios\(\lambda_1,\lambda_2,\ldots,\lambda_n\). Definir\(C\) como arriba, así\(C\) es invertible por el Teorema 5.1.1 en la Sección 5.1. Que\(D = C^{-1} A C\text{,}\) así\(A = CDC^{-1}\). Multiplicando por vectores de coordenadas estándar, Fact 3.3.2 en la Sección 3.3, escoge las columnas de\(Ce_i = v_i\text{,}\) lo\(C\text{:}\) tenemos\(e_i = C^{-1} v_i\). Multiplicamos por los vectores de coordenadas estándar para encontrar las columnas de\(D\text{:}\)
\[ De_i = C^{-1} A Ce_i = C^{-1} Av_i = C^{-1}\lambda_i v_i = \lambda_iC^{-1} v_i = \lambda_ie_i. \nonumber \]
Por lo tanto, las columnas de\(D\) son múltiplos de los vectores de coordenadas estándar:
\[ D = \left(\begin{array}{ccccc}\lambda_{1}&0&\cdots &0&0\\ 0&\lambda_{2}&\cdots &0&0 \\ \vdots &\vdots &\ddots&\vdots&\vdots \\ 0&0&\cdots&\lambda_{n-1}&0 \\ 0&0&\cdots &0&\lambda_{n}\end{array}\right). \nonumber \]
Ahora supongamos que\(A = CDC^{-1}\text{,}\) donde\(C\) tiene columnas\(v_1,v_2,\ldots,v_n\text{,}\) y\(D\) es diagonal con entradas diagonales\(\lambda_1,\lambda_2,\ldots,\lambda_n\). Dado que\(C\) es invertible, sus columnas son linealmente independientes. Tenemos que demostrar que\(v_i\) es un vector propio de\(A\) con valor propio\(\lambda_i\). Sabemos que el vector de coordenadas estándar\(e_i\) es un vector propio de\(D\) con autovalor\(\lambda_i\text{,}\) así:
\[ Av_i = CDC^{-1} v_i = CDe_i = C\lambda_ie_i = \lambda_iCe_i = \lambda_i v_i. \nonumber \]
Por Fact 5.1.1 en la Sección 5.1, si una\(n\times n\) matriz\(A\) tiene valores propios\(n\) distintos,\(\lambda_1,\lambda_2,\ldots,\lambda_n\text{,}\) entonces la elección de los vectores propios correspondientes\(v_1,v_2,\ldots,v_n\) es automáticamente linealmente independiente.
Una\(n\times n\) matriz con valores propios\(n\) distintos es diagonalizable.
Aplicar teorema\(\PageIndex{1}\) a la matriz
\[ A = \left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right). \nonumber \]
Solución
Esta matriz diagonal es en particular superior-triangular, por lo que sus valores propios son las entradas diagonales\(1,2,3\). Los vectores de coordenadas estándar son valores propios de una matriz diagonal:
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\left(\begin{array}{c}1\\0\\0\end{array}\right)=1\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\quad\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\left(\begin{array}{c}0\\1\\0\end{array}\right)=2\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\nonumber\]
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\left(\begin{array}{c}0\\0\\1\end{array}\right)=3\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]
Por lo tanto, el teorema de diagonalización dice que\(A=CDC^{-1}\text{,}\) donde las columnas de\(C\) son los vectores de coordenadas estándar, y el\(D\) es la matriz diagonal con entradas\(1,2,3\text{:}\)
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)^{-1}.\nonumber\]
Esto solo nos dice que\(A\) es similar a sí mismo.
En realidad, el teorema de diagonalización no es completamente trivial ni siquiera para matrices diagonales. Si ponemos nuestros valores propios en el orden\(3,2,1\text{,}\) entonces los vectores propios correspondientes son\(e_3,e_2,e_1\text{,}\) así que también tenemos que\(A = C'D'(C')^{-1}\text{,}\) donde\(C'\) esta la matriz con columnas\(e_3,e_2,e_1\text{,}\) y\(D'\) es la matriz diagonal con entradas\(3,2,1\text{:}\)
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)=\left(\begin{array}{ccc}0&0&1\\0&1&0\\1&0&0\end{array}\right)\left(\begin{array}{ccc}3&0&0\\0&2&0\\0&0&1\end{array}\right)\left(\begin{array}{ccc}0&0&1\\0&1&0\\1&0&0\end{array}\right)^{-1}.\nonumber\]
En particular, las matrices
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\quad\text{and}\quad\left(\begin{array}{ccc}3&0&0\\0&2&0\\0&0&1\end{array}\right)\nonumber\]
son similares entre sí.
Vimos en el ejemplo anterior que cambiar el orden de los valores propios y vectores propios produce una diagonalización diferente de la misma matriz. Generalmente hay muchas formas diferentes de diagonalizar una matriz, correspondientes a diferentes ordenamientos de los valores propios de esa matriz. Lo importante es que los valores propios y los vectores propios tienen que ser listados en el mismo orden.
\[\begin{aligned}A&=\left(\begin{array}{ccc}|&|&|\\ v_1&v_2&v_3\\|&|&|\end{array}\right)\left(\begin{array}{ccc}\lambda_1&0&0\\0&\lambda_2&0\\0&0&\lambda_3\end{array}\right)\left(\begin{array}{ccc}|&|&|\\v_1&v_2&v_3\\ |&|&|\end{array}\right)^{-1} \\ &=\left(\begin{array}{ccc}|&|&|\\v_3&v_2&v_1 \\ |&|&|\end{array}\right)\left(\begin{array}{ccc}\lambda_3&0&0 \\ 0&\lambda_2&0 \\ 0&0&\lambda_1\end{array}\right) \left(\begin{array}{ccc}|&|&|\\v_3&v_2&v_1\\ |&|&|\end{array}\right)^{-1}.\end{aligned}\]
Existen otras formas de encontrar diferentes diagonalizaciones de una misma matriz. Por ejemplo, puedes escalar uno de los vectores propios por una constante\(c\text{:}\)
\[\begin{aligned}A&=\left(\begin{array}{ccc}|&|&|\\ v_1&v_2&v_3\\|&|&|\end{array}\right)\left(\begin{array}{ccc}\lambda_1&0&0\\0&\lambda_2&0\\0&0&\lambda_3\end{array}\right)\left(\begin{array}{ccc}|&|&|\\v_1&v_2&v_3\\ |&|&|\end{array}\right)^{-1} \\ &=\left(\begin{array}{ccc}|&|&|\\cv_1&v_2&v_3 \\ |&|&|\end{array}\right)\left(\begin{array}{ccc}\lambda_1&0&0 \\ 0&\lambda_2&0 \\ 0&0&\lambda_3\end{array}\right) \left(\begin{array}{ccc}|&|&|\\cv_1&v_2&v_3\\ |&|&|\end{array}\right)^{-1}.\end{aligned}\]
puedes encontrar una base completamente diferente para un espacio propio de dimensión al menos\(2\text{,}\) etc.
Diagonalizar la matriz
\[ A = \left(\begin{array}{cc}1/2&3/2\\3/2&1/2\end{array}\right). \nonumber \]
Solución
Necesitamos encontrar los valores propios y los vectores propios de\(A\). Primero calculamos el polinomio característico:
\[ f(\lambda) = \lambda^2-\text{Tr}(A)\lambda + \det(A) = \lambda^2-\lambda-2 = (\lambda+1)(\lambda-2). \nonumber \]
Por lo tanto, los valores propios son\(-1\) y\(2\). Necesitamos calcular vectores propios para cada valor propio. Empezamos con\(\lambda_1 = -1\text{:}\)
\[ (A + 1I_2)v = 0 \iff \left(\begin{array}{cc}3/2&3/2\\3/2&3/2\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&1\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica es\(x = -y\text{,}\) así\(v_1 = {-1\choose 1}\) es un vector propio con valor propio\(\lambda_1\). Ahora encontramos un vector propio con valor propio\(\lambda_2 = 2\text{:}\)
\[ (A-2I_2)v = 0 \iff \left(\begin{array}{cc}-3/2&3/2\\3/2&-3/2\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&-1\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica es\(x = y\text{,}\) así\(v_2 = {1\choose 1}\) es un vector propio con valor propio\(2\).
Los vectores propios\(v_1,v_2\) son linealmente independientes, por lo que el Teorema\(\PageIndex{1}\) dice que
\[ A = CDC^{-1} \qquad\text{for}\qquad C = \left(\begin{array}{cc}-1&1\\1&1\end{array}\right) \qquad D = \left(\begin{array}{cc}-1&0\\0&2\end{array}\right). \nonumber \]
Alternativamente, si elegimos\(2\) como nuestro primer valor propio, entonces
\[ A = C'D'(C')^{-1} \qquad\text{for}\qquad C' =\left(\begin{array}{cc}1&-1\\1&1\end{array}\right) \qquad D' = \left(\begin{array}{cc}2&0\\0&-1\end{array}\right). \nonumber \]
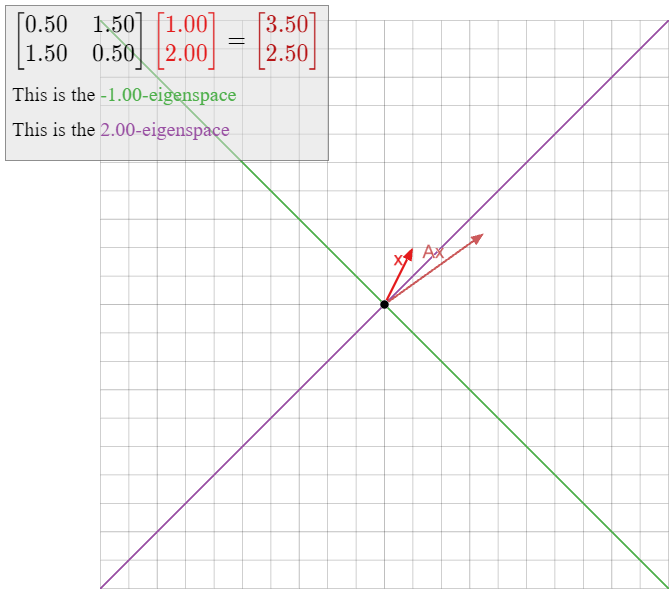
Diagonalizar la matriz
\[ A =\left(\begin{array}{cc}2/3&-4/3\\-2/3&4/3\end{array}\right). \nonumber \]
Solución
Necesitamos encontrar los valores propios y los vectores propios de\(A\). Primero calculamos el polinomio característico:
\[ f(\lambda) = \lambda^2-\text{Tr}(A)\lambda + \det(A) = \lambda^2 -2\lambda = \lambda(\lambda-2). \nonumber \]
Por lo tanto, los valores propios son\(0\) y\(2\). Necesitamos calcular vectores propios para cada valor propio. Empezamos con\(\lambda_1 = 0\text{:}\)
\[ (A - 0I_2)v = 0 \iff \left(\begin{array}{cc}2/3&-4/3\\-2/3&4/3\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&-2\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica es\(x = 2y\text{,}\) así\(v_1 = {2\choose 1}\) es un vector propio con valor propio\(\lambda_1\). Ahora encontramos un vector propio con valor propio\(\lambda_2 = 2\text{:}\)
\[ (A-2I_2)v = 0 \iff \left(\begin{array}{cc}-4/3&-4/3\\-2/3&-2/3\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&1\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica es\(x = -y\text{,}\) así\(v_2 = {1\choose-1}\) es un vector propio con valor propio\(2\).
Los vectores propios\(v_1,v_2\) son linealmente independientes, por lo que el Teorema\(\PageIndex{1}\) dice que
\[ A = CDC^{-1} \qquad\text{for}\qquad C =\left(\begin{array}{cc}2&1\\1&-1\end{array}\right) \qquad D = \left(\begin{array}{cc}0&0\\0&2\end{array}\right). \nonumber \]
Alternativamente, si elegimos\(2\) como nuestro primer valor propio, entonces
\[ A = C'D'(C')^{-1} \qquad\text{for}\qquad C' = \left(\begin{array}{cc}1&2\\-1&1\end{array}\right) \qquad D' = \left(\begin{array}{cc}2&0\\0&0\end{array}\right). \nonumber \]
En el ejemplo anterior, la matriz (no invertible)\(A = \frac 13\left(\begin{array}{cc}2&-4\\-2&4\end{array}\right)\) es similar a la matriz diagonal\(D = \left(\begin{array}{cc}0&0\\0&2\end{array}\right).\) Dado que no\(A\) es invertible, cero es un valor propio por el teorema de la matriz invertible, Teorema 5.1.1 en la Sección 5.1, por lo que una de las entradas diagonales de\(D\) es necesariamente cero. Ver también Ejemplo\(\PageIndex{10}\) a continuación.
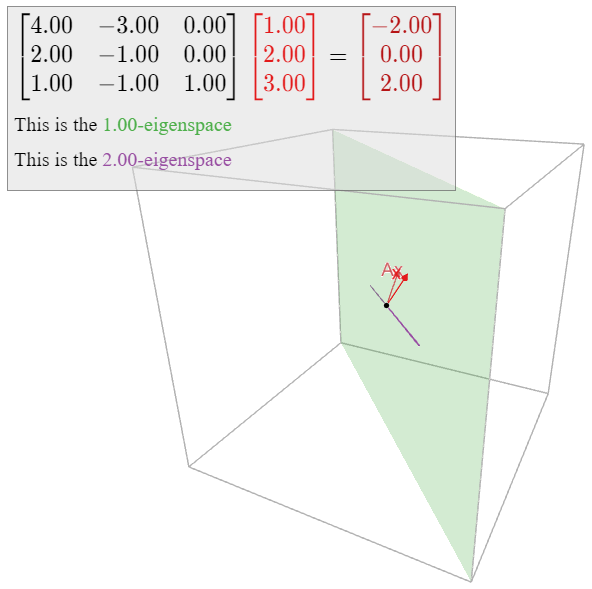
Diagonalizar la matriz
\[ A = \left(\begin{array}{ccc}4&-3&0\\2&-1&0\\1&-1&1\end{array}\right). \nonumber \]
Solución
Necesitamos encontrar los valores propios y los vectores propios de\(A\). Primero calculamos el polinomio característico expandiendo cofactores a lo largo de la tercera columna:
\[ \begin{split} f(\lambda) \amp= \det(A-\lambda I_3) = (1-\lambda)\det\left(\left(\begin{array}{cc}4&-3\\2&-1\end{array}\right) - \lambda I_2\right) \\ \amp= (1-\lambda)(\lambda^2 - 3\lambda + 2) = -(\lambda-1)^2(\lambda-2). \end{split} \nonumber \]
Por lo tanto, los valores propios son\(1\) y\(2\). Necesitamos calcular vectores propios para cada valor propio. Empezamos con\(\lambda_1 = 1\text{:}\)
\[ (A-I_3)v = 0 \iff \left(\begin{array}{ccc}3&-3&0\\2&-2&0\\1&-1&0\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{ccc}1&-1&0\\0&0&0\\0&0&0\end{array}\right)v = 0. \nonumber \]
La forma vectorial paramétrica es
\[\left\{\begin{array}{rrr}x&=&y \\ y&=&y \\ z&=&z \end{array}\right.\implies\left(\begin{array}{c}x\\y\\z\end{array}\right)+y\left(\begin{array}{c}1\\1\\0\end{array}\right)+z\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]
De ahí que una base para\(1\) el espacio propio es
\[\mathcal{B}_{1}=\{v_1,\:v_2\}\quad\text{where}\quad v_1=\left(\begin{array}{c}1\\1\\0\end{array}\right),\quad v_2=\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]
Ahora calculamos el espacio propio para\(\lambda_2 = 2\text{:}\)
\[ (A-2I_3)v = 0 \iff \left(\begin{array}{ccc}2&-3&0\\2&-3&0\\1&-1&-1\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{ccc}1&0&-3\\0&1&-2\\0&0&0\end{array}\right)v = 0 \nonumber \]
La forma paramétrica es\(x = 3z, y = 2z\text{,}\) así que un vector propio con valor propio\(2\) es
\[ v_3 = \left(\begin{array}{c}3\\2\\1\end{array}\right). \nonumber \]
Los vectores propios\(v_1,v_2,v_3\) son linealmente independientes:\(v_1,v_2\) forman una base para el\(1\) -espacio propio, y\(v_3\) no están contenidos en el\(1\) -espacio propio porque su valor propio es\(2\). Por lo tanto, Teorema\(\PageIndex{1}\) dice que
\[ A = CDC^{-1} \qquad\text{for}\qquad C = \left(\begin{array}{ccc}1&0&3\\1&0&2\\0&1&1\end{array}\right) \qquad D = \left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}\right). \nonumber \]
Aquí está el procedimiento que utilizamos en los ejemplos anteriores.
\(A\)Déjese ser una\(n\times n\) matriz. Para diagonalizar\(A\text{:}\)
- Encuentra los valores propios de\(A\) usar el polinomio característico.
- Para cada valor propio\(\lambda\) de\(A\text{,}\) calcular una base\(\mathcal{B}_\lambda\) para el\(\lambda\) -espacio propio.
- Si hay menos vectores que el\(n\) total en todas las bases del espacio propio\(B_\lambda\text{,}\), entonces la matriz no es diagonalizable.
- De lo contrario, los\(n\) vectores\(v_1,v_2,\ldots,v_n\) en las bases del espacio propio son linealmente independientes, y\(A = CDC^{-1}\) para\[C=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1&v_2&\cdots &v_n \\ |&|&\quad &|\end{array}\right)\quad\text{and}\quad D=\left(\begin{array}{cccc}\lambda_1&0&\cdots &0 \\ 0&\lambda_2&\cdots &0 \\ \vdots&\vdots &\ddots&\vdots \\ 0&0&\cdots &\lambda_n\end{array}\right),\nonumber\] dónde\(\lambda_i\) está el valor propio para\(v_i\).
Justificaremos la afirmación de independencia lineal en la parte 4 en la prueba del Teorema\(\PageIndex{3}\) a continuación.
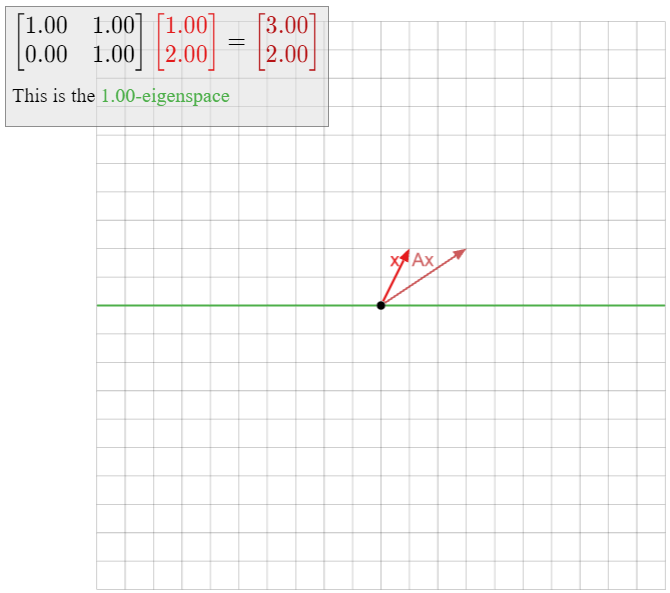
Let
\[ A = \left(\begin{array}{cc}1&1\\0&1\end{array}\right), \nonumber \]
así\(T(x) = Ax\) es una cizalla, Ejemplo 3.1.8 en la Sección 3.1. El polinomio característico de\(A\) es\(f(\lambda) = (\lambda-1)^2\text{,}\) por lo que el único valor propio de\(A\) es\(1\). Calculamos el\(1\) -eigenspace:
\[ (A - I_2)v = 0 \iff \left(\begin{array}{cc}0&1\\0&0\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)= 0 \iff y = 0. \nonumber \]
En otras palabras, el\(1\) -espacio propio es exactamente el\(x\) -eje, por lo que todos los vectores propios de se\(A\) encuentran en el\(x\) eje -eje. De ello se deduce que\(A\) no admite dos vectores propios linealmente independientes, por lo que por Teorema\(\PageIndex{1}\), no es diagonalizable.
En el Ejemplo 5.1.8 de la Sección 5.1, estudiamos los valores propios de una cizalla geométricamente; reproducimos aquí la demostración interactiva.
Dejar\(L\) ser una línea a través del origen en\(\mathbb{R}^2 \text{,}\) y definir\(T\colon\mathbb{R}^2 \to\mathbb{R}^2 \) para ser la transformación que envía un vector\(x\) al punto más cercano\(L\) a\(x\text{,}\) como en la imagen de abajo.
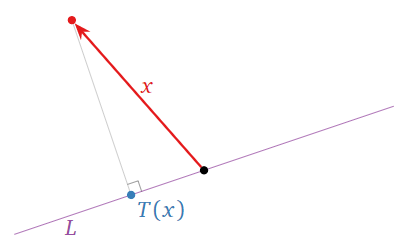
Figura\(\PageIndex{4}\)
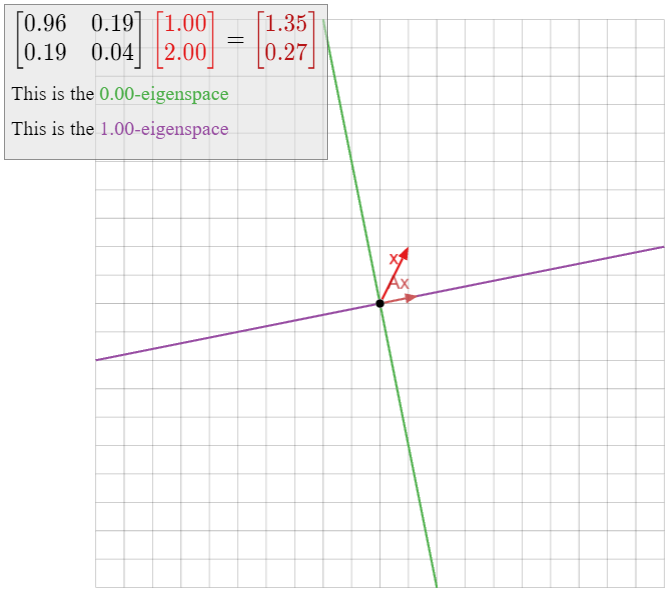
Este es un ejemplo de una proyección ortogonal. Veremos en la Sección 6.3 que\(T\) es una transformación lineal; deja\(A\) ser la matriz para\(T\). Cualquier vector encendido no\(L\) es movido por\(T\) porque es el punto más cercano\(L\) a sí mismo: de ahí es un vector propio de\(A\) con valor propio\(1\). Dejar\(L^\perp\) ser la línea perpendicular a\(L\) y que pasa por el origen. Cualquier vector\(x\) en\(L^\perp\) es el más cercano al vector cero en\(L\text{,}\) así que un (distinto de cero) tal vector es un vector propio de\(A\) con valor propio\(0\). (Véase el Ejemplo 5.1.5 en la Sección 5.1 para un caso especial.) Ya que\(A\) tiene dos valores propios distintos, es diagonalizable; de hecho, sabemos por Teorema\(\PageIndex{1}\) que\(A\) es similar a la matriz\(\left(\begin{array}{cc}1&0\\0&0\end{array}\right)\).
¡Tenga en cuenta que nunca tuvimos que hacer álgebra! Sabemos que\(A\) es diagonalizable por razones geométricas.
Let
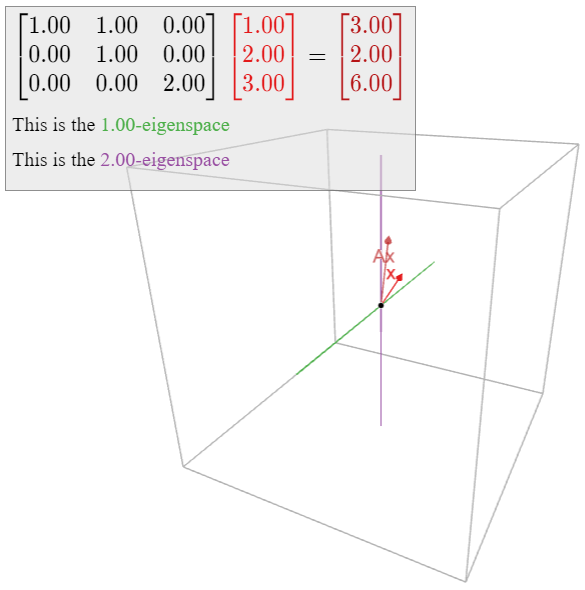
\[ A =\left(\begin{array}{ccc}1&1&0\\0&1&0\\0&0&2\end{array}\right). \nonumber \]
El polinomio característico de\(A\) es\(f(\lambda) = -(\lambda-1)^2(\lambda-2)\text{,}\) así que los valores propios de\(A\) son\(1\) y\(2\). Calculamos el\(1\) -eigenspace:
\[ (A - I_3)v = 0 \iff \left(\begin{array}{ccc}0&1&0\\0&0&0\\0&0&2\end{array}\right)\left(\begin{array}{c}x\\y\\z\end{array}\right) = 0 \iff y = z = 0. \nonumber \]
En otras palabras, el\(1\) -espacio propio es el\(x\) -eje. Del mismo modo,
\[ (A - 2I_3)v = 0 \iff \left(\begin{array}{ccc}-1&1&0\\0&-1&0\\0&0&0\end{array}\right)\left(\begin{array}{c}x\\y\\z\end{array}\right) = 0 \iff x = y = 0, \nonumber \]
así que el espacio\(2\) -eigenspace es el\(z\) eje -. En particular, todos los vectores propios de se\(A\) encuentran en el\(xz\) plano -plano, por lo que no existen tres vectores propios linealmente independientes de\(A\). Por teorema\(\PageIndex{1}\), la matriz no\(A\) es diagonalizable.
Observe que\(A\) contiene un\(2\times 2\) bloque en su diagonal que parece una cizalla:
\[A=\left(\begin{array}{ccc}\color{Red}{1}&\color{Red}{1}&\color{black}{0}\\ \color{Red}{0}&\color{Red}{1}&\color{black}{0} \\ 0&0&2\end{array}\right).\nonumber\]
Esto hace sospechar que tal matriz no es diagonalizable.
Let
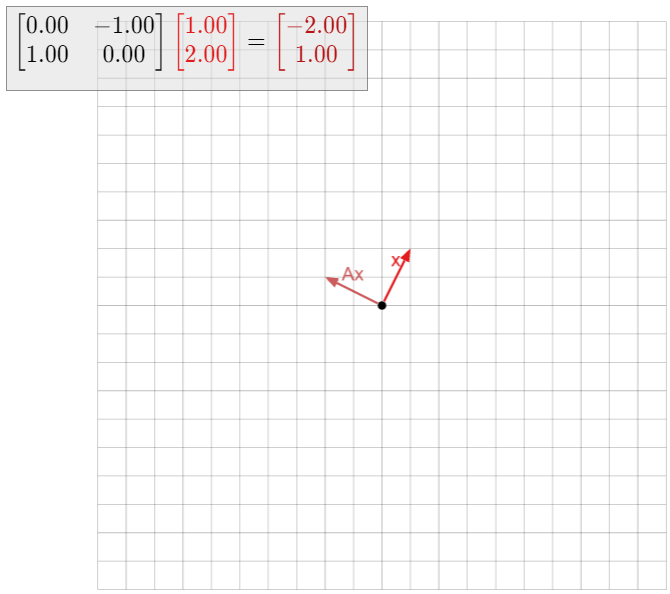
\[ A = \left(\begin{array}{cc}0&-1\\1&0\end{array}\right), \nonumber \]
así\(T(x) = Ax\) es la transformación lineal que gira en sentido antihorario por\(90^\circ\). Vimos en el Ejemplo 5.1.9 en la Sección 5.1 que\(A\) no tiene ningún vector propio en absoluto. De ello se deduce que no\(A\) es diagonalizable.
El polinomio característico de\(A\) es\(f(\lambda) = \lambda^2+1\text{,}\) el que por supuesto no tiene raíces reales. Si permitimos números complejos, sin embargo, entonces\(f\) tiene dos raíces, a saber,\(\pm i\text{,}\) dónde\(i = \sqrt{-1}\). De ahí que la matriz sea diagonalizable si nos permitimos usar números complejos. Trataremos este tema en detalle en la Sección 5.5.
El siguiente punto suele ser fuente de confusión.
De las siguientes matrices, la primera es diagonalizable e invertible, la segunda es diagonalizable pero no invertible, la tercera es invertible pero no diagonalizable, y la cuarta no es invertible ni diagonalizable, ya que el lector puede verificar:
\[\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\quad\left(\begin{array}{cc}1&0\\0&0\end{array}\right)\quad\left(\begin{array}{cc}1&1\\0&1\end{array}\right)\quad\left(\begin{array}{cc}0&1\\0&0\end{array}\right).\nonumber\]
Como en el Ejemplo anterior\(\PageIndex{9}\), se puede comprobar que la matriz
\[ A_\lambda = \left(\begin{array}{cc}\lambda&1\\0&\lambda\end{array}\right) \nonumber \]
no es diagonalizable para ningún número\(\lambda\). Afirmamos que cualquier\(2\times 2\) matriz no diagonalizable\(B\) con un valor propio real\(\lambda\) es similar a\(A_\lambda\). Por lo tanto, hasta la similitud, estos son los únicos ejemplos de este tipo.
Para probarlo, dejemos\(B\) ser tal matriz. Dejar\(v_1\) ser un vector propio con valor propio\(\lambda\text{,}\) y dejar\(v_2\) ser cualquier vector en el\(\mathbb{R}^2 \) que no sea colineal con\(v_1\text{,}\) lo que\(\{v_1,v_2\}\) forma una base para\(\mathbb{R}^2 \). Dejar\(C\) ser la matriz con columnas\(v_1,v_2\text{,}\) y considerar\(A = C^{-1} BC\). Tenemos\(Ce_1=v_1\) y\(Ce_2=v_2\text{,}\) así\(C^{-1} v_1=e_1\) y\(C^{-1} v_2=e_2\). Podemos calcular la primera columna de la\(A\) siguiente manera:
\[ Ae_1 = C^{-1} BC e_1 = C^{-1} Bv_1 = C^{-1}\lambda v_1 = \lambda C^{-1} v_1 = \lambda e_1. \nonumber \]
Por lo tanto,\(A\) tiene la forma
\[ A = \left(\begin{array}{cc}\lambda&b\\0&d\end{array}\right). \nonumber \]
Ya que\(A\) es similar a\(B\text{,}\) ella también tiene un solo valor propio\(\lambda\text{;}\) ya que\(A\) es superior-triangular, esto implica\(d=\lambda\text{,}\) así
\[ A = \left(\begin{array}{cc}\lambda&b\\0&\lambda\end{array}\right). \nonumber \]
Como no\(B\) es diagonalizable, sabemos que no\(A\) es diagonal (\(B\)es similar a\(A\)), entonces\(b\neq 0\). Ahora observamos que
\[\left(\begin{array}{cc}1/b&0\\0&1\end{array}\right)\left(\begin{array}{cc}\lambda&b\\0&\lambda\end{array}\right)\left(\begin{array}{cc}1/b&0\\0&1\end{array}\right)^{-1}=\left(\begin{array}{cc}\lambda /b&1 \\ 0&\lambda\end{array}\right)\left(\begin{array}{cc}b&0\\0&1\end{array}\right)=\left(\begin{array}{cc}\lambda&1 \\ 0&\lambda\end{array}\right)=A_{\lambda}.\nonumber\]
Hemos demostrado que\(B\) es similar a\(A\text{,}\) lo que es similar a\(A_\lambda\text{,}\) lo que\(B\) es similar a\(A_\lambda\) por la propiedad de transitividad, Proposición 5.3.1 en la Sección 5.3, de matrices similares.
La geometría de las matrices diagonalizables
Una matriz diagonal es fácil de entender geométricamente, ya que solo escala los ejes de coordenadas:
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\left(\begin{array}{c}1\\0\\0\end{array}\right)=1\cdot\left(\begin{array}{c}1\\0\\0\end{array}\right)\quad\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\left(\begin{array}{c}0\\1\\0\end{array}\right)=2\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)\nonumber\]
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)\left(\begin{array}{c}0\\0\\1\end{array}\right)=3\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]
Por lo tanto, sabemos por la Sección 5.3 que una matriz diagonalizable simplemente escala los “ejes” con respecto a un sistema de coordenadas diferente. De hecho, si\(v_1,v_2,\ldots,v_n\) son vectores propios linealmente independientes de una\(n\times n\) matriz\(A\text{,}\), entonces\(A\) escala la\(v_i\) -dirección por el valor propio\(\lambda_i\).
En los siguientes ejemplos, visualizamos la acción de una matriz diagonalizable\(A\) en términos de su dinámica. Es decir, comenzamos con una colección de vectores (dibujados como puntos), y vemos por dónde se mueven cuando los multiplicamos por\(A\) repetidamente.
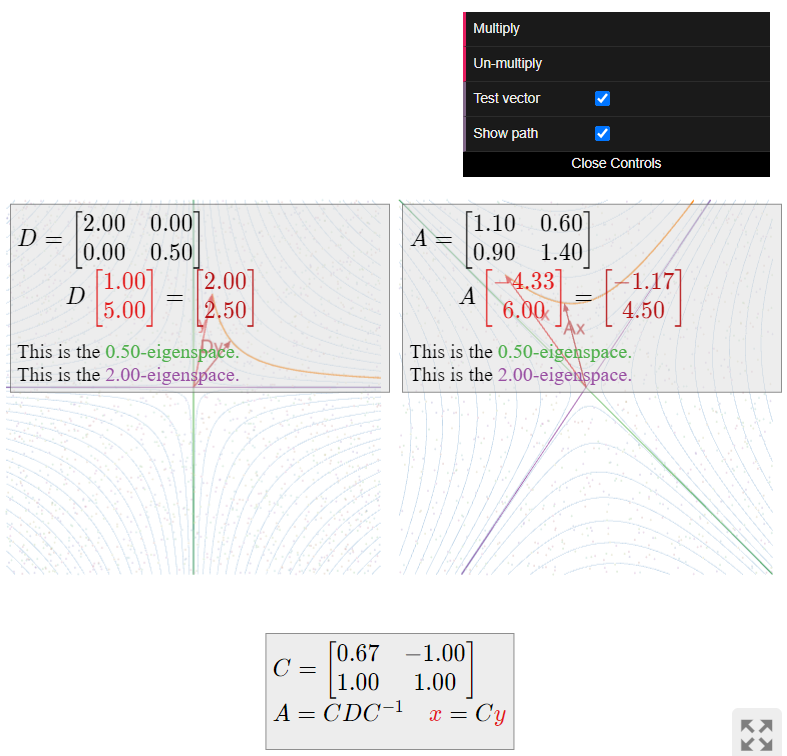
Describir cómo la matriz
\[ A = \frac{1}{10}\left(\begin{array}{cc}11&6\\9&14\end{array}\right) \nonumber \]
actúa en el avión.
Solución
Primero diagonalizamos\(A\). El polinomio característico es
\[ f(\lambda) = \lambda^2 - \text{Tr}(A)\lambda + \det(A) = \lambda^2 - \frac 52\lambda + 1 = (\lambda - 2)\left(\lambda - \frac 12\right). \nonumber \]
Calculamos el\(2\) -eigenspace:
\[ (A-2I_3)v = 0 \iff \frac 1{10}\left(\begin{array}{cc}-9&6\\9&-6\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&-2/3\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica de esta ecuación es\(x = 2/3y\text{,}\) así que un vector propio es\(v_1 = {2/3\choose 1}\). Para el\(1/2\) -eigenspace, tenemos:
\[ \left(A-\frac 12I_3\right)v = 0 \iff \frac 1{10}\left(\begin{array}{cc}6&6\\9&9\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&1\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica de esta ecuación es\(x = -y\text{,}\) así que un vector propio es\(v_2 = {-1\choose 1}\). De ello se deduce que\(A = CDC^{-1}\text{,}\) donde
\[ C = \left(\begin{array}{cc}2/3&-1 \\ 1&1\end{array}\right) \qquad D = \left(\begin{array}{cc}2&0\\0&1/2\end{array}\right). \nonumber \]
La matriz diagonal\(D\) escala la\(x\) coordenada por\(2\) y la\(y\) coordenada por\(1/2\). Por lo tanto, mueve vectores más cerca del\(x\) eje -y más lejos del\(y\) eje -eje. De hecho, ya que\((2x)(y/2) = xy\text{,}\) la multiplicación por\(D\) no mueve un punto fuera de una hipérbola\(xy = C\).
La matriz\(A\) hace lo mismo, en el sistema\(v_1,v_2\) -coordenada: multiplicar un vector por\(A\) escalas la\(v_1\) -coordenada por\(2\) y la\(v_2\) -coordenada por\(1/2\). Por lo tanto,\(A\) mueve los vectores más cerca del\(2\) -espacio propio y más lejos del\(1/2\) -espacio propio.
Describir cómo la matriz
\[ A = \frac 1{5}\left(\begin{array}{cc}13&-2\\-3&12\end{array}\right) \nonumber \]
actúa en el avión.
Solución
Primero diagonalizamos\(A\). El polinomio característico es
\[ f(\lambda) = \lambda^2 - \text{Tr}(A)\lambda + \det(A) = \lambda^2 - 5\lambda + 6 = (\lambda - 2)(\lambda - 3). \nonumber \]
A continuación calculamos el\(2\) -eigenspace:
\[ (A-2I_3)v = 0 \iff \frac 15\left(\begin{array}{cc}3&-2\\-3&2\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&-2/3\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica de esta ecuación es\(x = 2/3y\text{,}\) así que un vector propio es\(v_1 = {2/3\choose 1}\). Para el\(3\) -eigenspace, tenemos:
\[ (A-3I_3)v = 0 \iff \frac 15\left(\begin{array}{cc}-2&-2\\-3&-3\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&1\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica de esta ecuación es\(x = -y\text{,}\) así que un vector propio es\(v_2 = {-1\choose 1}\). De ello se deduce que\(A = CDC^{-1}\text{,}\) donde
\[ C = \left(\begin{array}{cc}2/3&-1\\1&1\end{array}\right) \qquad D = \left(\begin{array}{cc}2&0\\0&3\end{array}\right). \nonumber \]
La matriz diagonal\(D\) escala la\(x\) coordenada por\(2\) y la\(y\) coordenada por\(3\). Por lo tanto, mueve vectores más lejos tanto del\(x\) eje -eje como del\(y\) eje -, pero más rápido en la\(y\) dirección -que en la\(x\) dirección -dirección.
La matriz\(A\) hace lo mismo, en el sistema\(v_1,v_2\) -coordenada: multiplicar un vector por\(A\) escalas la\(v_1\) -coordenada por\(2\) y la\(v_2\) -coordenada por\(3\). Por lo tanto,\(A\) mueve vectores más lejos del\(2\) -espacio propio y del\(3\) espacio -propio, pero más rápido en la\(v_2\) dirección -que en la\(v_1\) dirección -dirección.
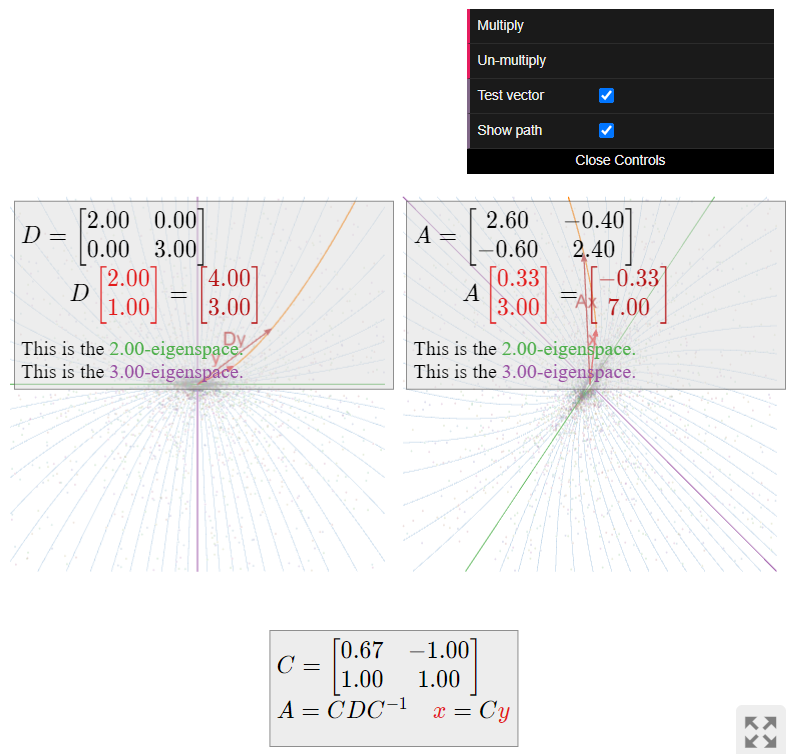
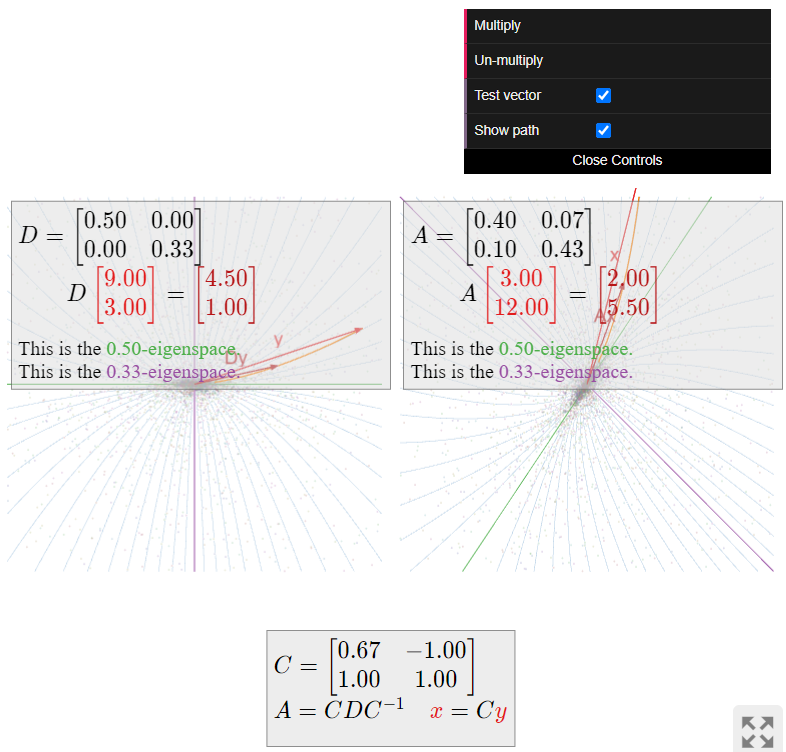
Describir cómo la matriz
\[ A' = \frac 1{30}\left(\begin{array}{cc}12&2\\3&13\end{array}\right) \nonumber \]
actúa en el avión.
Solución
Esta es la inversa de la matriz\(A\) del Ejemplo anterior\(\PageIndex{14}\). En ese ejemplo, encontramos\(A = CDC^{-1}\) para
\[ C = \left(\begin{array}{cc}2/3&-1\\1&1\end{array}\right) \qquad D = \left(\begin{array}{cc}2&0\\0&3\end{array}\right). \nonumber \]
Por lo tanto, recordando que tomar inversas invierte el orden de multiplicación, Hecho 3.5.1 en la Sección 3.5, tenemos
\[ A' = A^{-1} = (CDC^{-1})^{-1} = (C^{-1})^{-1} D^{-1} C^{-1} = C\left(\begin{array}{cc}1/2&0\\0&1/3\end{array}\right)C^{-1}. \nonumber \]
La matriz diagonal\(D^{-1}\) hace lo contrario de lo que\(D\) hace: escala la\(x\) coordenada por\(1/2\) y la\(y\) coordenada por\(1/3\). Por lo tanto, mueve vectores más cerca de ambos ejes de coordenadas, pero más rápido en la\(y\) dirección -dirección. La matriz\(A'\) hace lo mismo, pero con respecto al sistema\(v_1,v_2\) -coordenada.
Describir cómo la matriz
\[ A = \frac 16\left(\begin{array}{cc}5&-1\\-2&4\end{array}\right) \nonumber \]
actúa en el avión.
Solución
Primero diagonalizamos\(A\). El polinomio característico es
\[ f(\lambda) = \lambda^2 - \text{Tr}(A)\lambda + \det(A) = \lambda^2 - \frac 32\lambda + \frac 12 = (\lambda - 1)\left(\lambda - \frac 12\right). \nonumber \]
A continuación calculamos el\(1\) -eigenspace:
\[ (A-I_3)v = 0 \iff \frac 16\left(\begin{array}{cc}-1&-1\\-2&-2\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&1\\0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica de esta ecuación es\(x = -y\text{,}\) así que un vector propio es\(v_1 = {-1\choose 1}\). Para el\(1/2\) -eigenspace, tenemos:
\[ \left(A-\frac 12I_3\right)v = 0 \iff \frac 16\left(\begin{array}{cc}2&-1\\-2&1\end{array}\right)v = 0 \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{cc}1&-1/2 \\ 0&0\end{array}\right)v = 0. \nonumber \]
La forma paramétrica de esta ecuación es\(x = 1/2y\text{,}\) así que un vector propio es\(v_2 = {1/2\choose 1}\). De ello se deduce que\(A = CDC^{-1}\text{,}\) donde
\[ C = \left(\begin{array}{cc}-1&1/2 \\ 1&1\end{array}\right) \qquad D = \left(\begin{array}{cc}1&0\\0&1/2\end{array}\right). \nonumber \]
La matriz diagonal\(D\) escala la\(y\) coordenada -por\(1/2\) y no mueve la\(x\) coordenada -. Por lo tanto, simplemente mueve vectores más cerca del\(x\) eje -a lo largo de líneas verticales. La matriz\(A\) hace lo mismo, en el sistema\(v_1,v_2\) -coordenada: multiplicar un vector por\(A\) escalas la\(v_2\) coordenada -por\(1/2\) y no cambia la\(v_1\) coordenada -. Por lo tanto,\(A\) “chupa vectores en el\(1\) -espacio propio” a lo largo de líneas paralelas a\(v_2\).
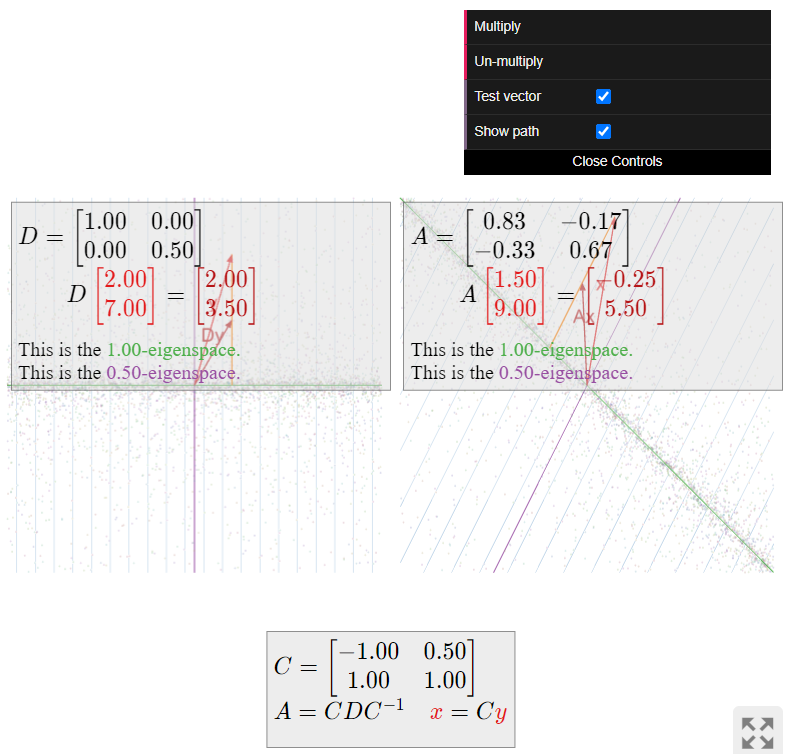
La matriz diagonal
\[ D = \left(\begin{array}{ccc}1/2&0&0\\0&2&0\\0&0&3/2\end{array}\right) \nonumber \]
escala la\(x\) coordenada -por\(1/2\text{,}\) la\(y\) coordenada -por\(2\text{,}\) y la\(z\) coordenada -por\(3/2\). Mirando hacia abajo al\(xy\) plano, los puntos siguen caminos parabólicos alejándolos del\(x\) eje -y hacia el\(y\) eje -eje. La\(z\) coordenada -se escala por\(3/2\text{,}\) lo que los puntos vuelan lejos del\(xy\) -plano en esa dirección.
Si\(A = CDC^{-1}\) para alguna matriz invertible\(C\text{,}\) entonces\(A\) hace lo mismo que\(D\text{,}\) pero con respecto al sistema de coordenadas definido por las columnas de\(C\).
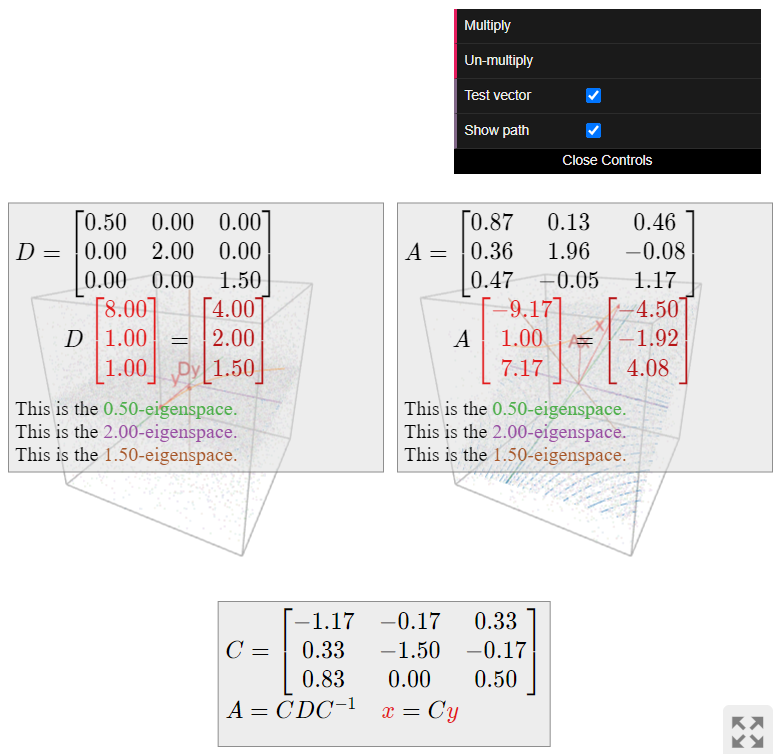
Multiplicidad algebraica y geométrica
En esta subsección, damos una variante del Teorema\(\PageIndex{1}\) que proporciona otro criterio para la diagonalizabilidad. Se afirma en el lenguaje de las multiplicidades de los valores propios.
En álgebra, definimos la multiplicidad\(\lambda_0\) de una raíz de un polinomio\(f(\lambda)\) como el número de factores de\(\lambda-\lambda_0\) esa división\(f(\lambda).\) Por ejemplo, en el polinomio
\[ f(\lambda) = -\lambda^3 + 4\lambda^2 - 5\lambda + 2 = -(\lambda-1)^2(\lambda-2), \nonumber \]
la raíz\(\lambda_0=2\) tiene multiplicidad\(1\text{,}\) y la raíz\(\lambda_0=1\) tiene multiplicidad\(2\).
Dejar\(A\) ser una\(n\times n\) matriz, y dejar\(\lambda\) ser un valor propio de\(A\).
- La multiplicidad algebraica de\(\lambda\) es su multiplicidad como raíz del polinomio característico de\(A\).
- La multiplicidad geométrica de\(\lambda\) es la dimensión\(\lambda\) del espacio propio.
Dado que el\(\lambda\) -espacio propio de\(A\) es\(\text{Nul}(A-\lambda I_n)\text{,}\) su dimensión es el número de variables libres en el sistema de ecuaciones\((A - \lambda I_n)x=0\text{,}\) es decir, el número de columnas sin pivotes en la matriz\(A-\lambda I_n\).
La matriz de cizallamiento
\[ A = \left(\begin{array}{cc}1&1\\0&1\end{array}\right) \nonumber \]
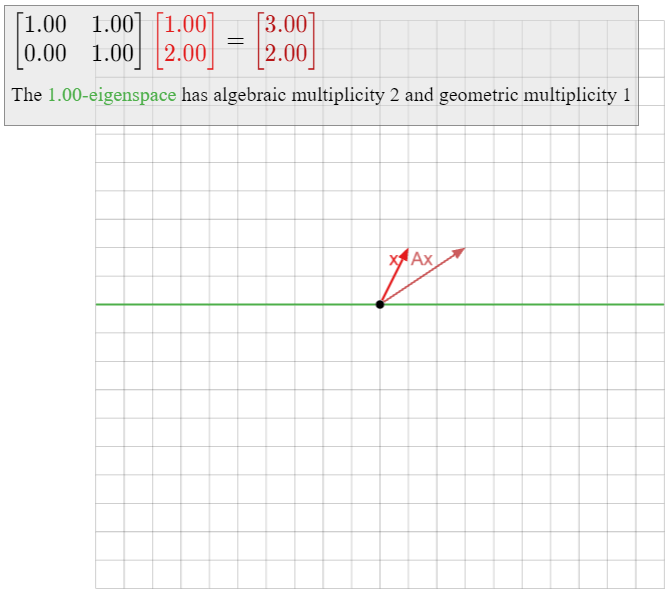
tiene sólo un valor propio\(\lambda=1\). El polinomio característico de\(A\) es\(f(\lambda) = (\lambda-1)^2\text{,}\) así\(1\) tiene multiplicidad algebraica\(2\text{,}\) ya que es una raíz doble de\(f\). Por otro lado, mostramos en Ejemplo\(\PageIndex{9}\) que el\(1\) -espacio propio de\(A\) es el\(x\) -eje, por lo que la multiplicidad geométrica de\(1\) es igual a\(1\). Esta matriz no es diagonalizable.
La matriz de identidad
\[ I_2 = \left(\begin{array}{cc}1&0\\0&1\end{array}\right) \nonumber \]
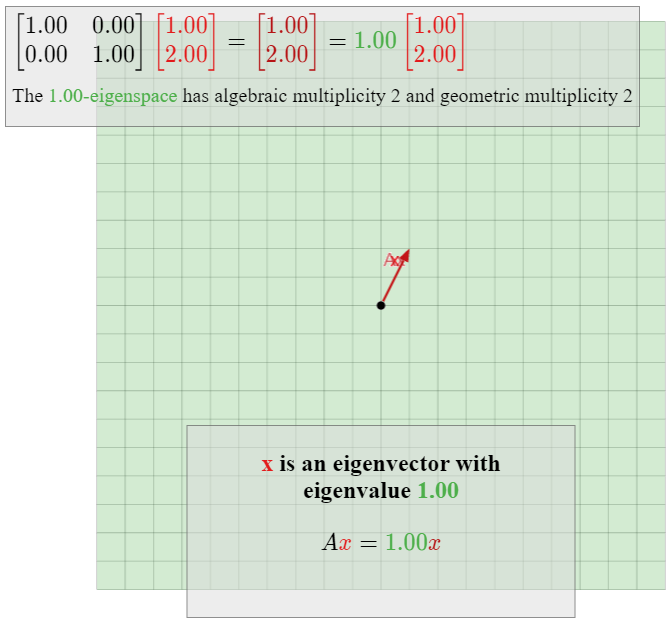
también tiene polinomio característico\((\lambda-1)^2\text{,}\) por lo que el valor propio\(1\) tiene multiplicidad algebraica\(2\). Dado que cada vector distinto de cero en\(\mathbb{R}^2 \) es un vector propio de\(I_2\) con autovalor,\(1\text{,}\) el espacio\(1\) -eigenspace es todo\(\mathbb{R}^2 \text{,}\) así que la multiplicidad geométrica también\(2\) lo es. Esta matriz es diagonal.
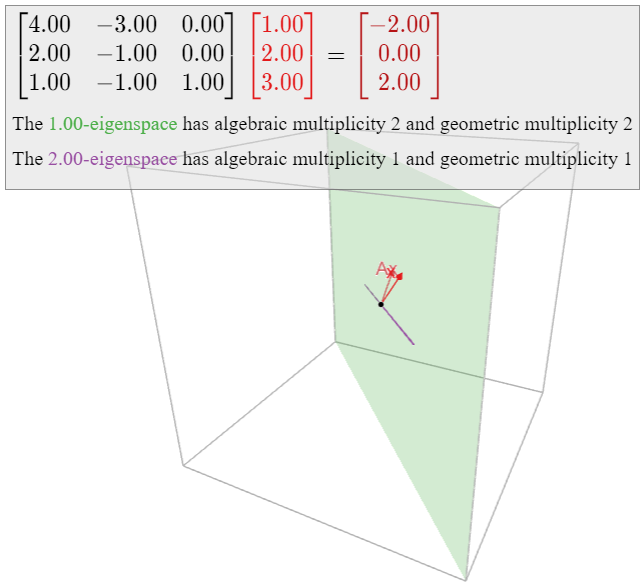
Continuando con el Ejemplo\(\PageIndex{8}\), vamos
\[ A = \left(\begin{array}{ccc}4&-2&0\\2&-1&0\\1&-1&1\end{array}\right). \nonumber \]
El polinomio característico es\(f(\lambda) = -(\lambda-1)^2(\lambda-2)\text{,}\) así que\(1\) y\(2\) son los valores propios, con multiplicidades algebraicas\(2\) y\(1\text{,}\) respectivamente. Se computó que el\(1\) -espacio propio es un plano y el\(2\) -espacio propio es una línea, de manera que\(1\) y\(2\) también tienen multiplicidades geométricas\(2\) y\(1\text{,}\) respectivamente. Esta matriz es diagonalizable.
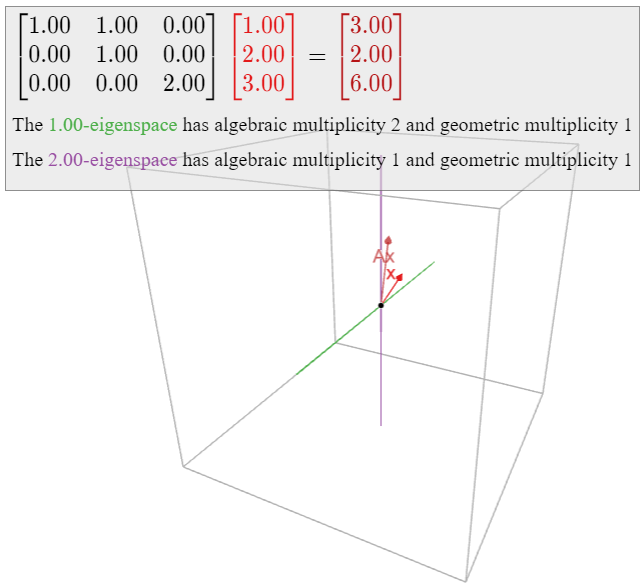
En Ejemplo\(\PageIndex{11}\), vimos que la matriz
\[ A = \left(\begin{array}{ccc}1&1&0\\0&1&0\\0&0&2\end{array}\right) \nonumber \]
también tiene polinomio característico de\(f(\lambda) = -(\lambda-1)^2(\lambda-2)\text{,}\) manera que\(1\) y\(2\) son los valores propios, con multiplicidades algebraicas\(2\) y\(1\text{,}\) respectivamente. En este caso, sin embargo, ambos espacios propios son líneas, de manera que ambos valores propios tienen multiplicidad geométrica\(1\). Esta matriz no es diagonalizable.
Vimos en los ejemplos anteriores que las multiplicidades algebraicas y geométricas no necesitan coincidir. No obstante, sí satisfacen la siguiente desigualdad fundamental, cuya prueba está más allá del alcance de este texto.
Dejar\(A\) ser una matriz cuadrada y dejar\(\lambda\) ser un valor propio de\(A\). Entonces
\[ 1 \leq \text{(the geometric multiplicity of $\lambda$)} \leq \text{(the algebraic multiplicity of $\lambda$)}. \nonumber \]
En particular, si la multiplicidad algebraica de\(\lambda\) es igual a\(1\text{,}\) entonces también lo es la multiplicidad geométrica.
Si\(A\) tiene un valor propio\(\lambda\) con multiplicidad algebraica\(1\text{,}\) entonces el\(\lambda\) -espacio propio es una línea.
Podemos utilizar el Teorema\(\PageIndex{2}\) para dar otro criterio para la diagonalizabilidad (además del Teorema\(\PageIndex{1}\)).
\(A\)Déjese ser una\(n\times n\) matriz. Los siguientes son equivalentes:
- \(A\)es diagonalizable.
- La suma de las multiplicidades geométricas de los valores propios de\(A\) es igual a\(n\).
- La suma de las multiplicidades algebraicas de los valores propios de\(A\) es igual a\(n\text{,}\) y para cada valor propio, la multiplicidad geométrica es igual a la multiplicidad algebraica.
- Prueba
-
Vamos a mostrar\(1\implies 2\implies 3\implies 1\). Primero supongamos que\(A\) es diagonalizable. Entonces\(A\) tiene vectores propios\(n\) linealmente independientes\(v_1,v_2,\ldots,v_n\). Esto implica que la suma de las multiplicidades geométricas es al menos\(n\text{:}\) por ejemplo, si\(v_1,v_2,v_3\) tienen el mismo valor propio\(\lambda\text{,}\) entonces la multiplicidad geométrica de\(\lambda\) es al menos\(3\) (ya que el\(\lambda\) -espacio propio contiene tres vectores linealmente independientes), y así sucesivamente. Pero la suma de las multiplicidades algebraicas es mayor o igual que la suma de las multiplicidades geométricas por Teorema\(\PageIndex{2}\), y la suma de las multiplicidades algebraicas es a lo sumo\(n\) porque el polinomio característico tiene grado\(n\). Por lo tanto, la suma de las multiplicidades geométricas es igual\(n\).
Ahora supongamos que la suma de las multiplicidades geométricas es igual\(n\). Como antes, esto obliga a la suma de las multiplicidades algebraicas a igualar\(n\) también. Como las multiplicidades algebraicas son todas mayores o iguales a las multiplicidades geométricas en cualquier caso, esto implica que de hecho son iguales.
Por último, supongamos que se cumple la tercera condición. Entonces la suma de las multiplicidades geométricas es igual\(n\). Supongamos que los vectores propios distintos son\(\lambda_1,\lambda_2,\ldots,\lambda_k\text{,}\) y eso\(\mathcal{B}_i\) es una base para el\(\lambda_i\) -espacio propio, al que llamamos\(V_i\). Afirmamos que la colección\(\mathcal{B} = \{v_1,v_2,\ldots,v_n\}\) de todos los vectores en todas las bases del espacio propio\(\mathcal{B}_i\) es linealmente independiente. Considerar la ecuación vectorial
\[ 0 = c_1v_1 + c_2v_2 + \cdots + c_nv_n. \nonumber \]
Agrupando los vectores propios con los mismos valores propios, esta suma tiene la forma
\[ 0 = \text{(something in $V_1$)} + \text{(something in $V_2$)} + \cdots + \text{(something in $V_k$)}. \nonumber \]
Dado que los vectores propios con valores propios distintos son linealmente independientes, Fact 5.1.1 en la Sección 5.1, cada “algo en\(V_i\)” es igual a cero. Pero esto implica que todos los coeficientes\(c_1,c_2,\ldots,c_n\) son iguales a cero, ya que los vectores en cada uno\(\mathcal{B}_i\) son linealmente independientes. Por lo tanto,\(A\) tiene vectores propios\(n\) linealmente independientes, por lo que es diagonalizable.
La primera parte de la tercera afirmación simplemente dice que el polinomio característico de\(A\) los factores completamente en polinomios lineales sobre los números reales: en otras palabras, no hay raíces complejas (no reales). La segunda parte del tercer enunciado dice en particular que para cualquier matriz diagonalizable, coinciden las multiplicidades algebraicas y geométricas.
Dejar\(A\) ser una matriz cuadrada y dejar\(\lambda\) ser un valor propio de\(A\). Si la multiplicidad algebraica de\(\lambda\) no es igual a la multiplicidad geométrica, entonces no\(A\) es diagonalizable.
Los ejemplos al inicio de esta subsección ilustran el teorema. Aquí damos algunas consecuencias generales para la diagonalizabilidad de\(2\times 2\) y\(3\times 3\) matrices.
\(A\)Déjese ser una\(2\times 2\) matriz. Hay cuatro casos:
- \(A\)tiene dos valores propios diferentes. En este caso, cada valor propio tiene multiplicidad algebraica y geométrica igual a uno. Esto implica que\(A\) es diagonalizable. Por ejemplo:\[A=\left(\begin{array}{cc}1&7\\0&2\end{array}\right).\nonumber\]
- \(A\)tiene un valor propio\(\lambda\) de multiplicidad algebraica y geométrica\(2\). Decir que la multiplicidad geométrica es\(2\) significa que\(\text{Nul}(A-\lambda I_2) = \mathbb{R}^2 \text{,}\) es decir, que cada vector en\(\mathbb{R}^2 \) está en el espacio nulo de\(A-\lambda I_2\). Esto implica que\(A-\lambda I_2\) es la matriz cero, así que esa\(A\) es la matriz diagonal\(\lambda I_2\). En particular,\(A\) es diagonalizable. Por ejemplo:\[A=\left(\begin{array}{cc}1&0\\0&1\end{array}\right).\nonumber\]
- \(A\)tiene un valor propio\(\lambda\) de multiplicidad algebraica\(2\) y multiplicidad geométrica\(1\). En este caso, no\(A\) es diagonalizable, por la parte 3 del Teorema\(\PageIndex{3}\). Por ejemplo, una cizalla:\[A=\left(\begin{array}{cc}1&1\\0&1\end{array}\right).\nonumber\]
- \(A\)no tiene valores propios. Esto sucede cuando el polinomio característico no tiene raíces reales. En particular, no\(A\) es diagonalizable. Por ejemplo, una rotación:\[A=\left(\begin{array}{cc}1&-1\\1&1\end{array}\right).\nonumber\]
\(A\)Déjese ser una\(3\times 3\) matriz. Podemos analizar la diagonalizabilidad\(A\) de caso por caso, como en el Ejemplo anterior\(\PageIndex{20}\).
- \(A\)tiene tres valores propios diferentes. En este caso, cada valor propio tiene multiplicidad algebraica y geométrica igual a uno. Esto implica que\(A\) es diagonalizable. Por ejemplo:\[A=\left(\begin{array}{ccc}1&7&4\\0&2&3\\0&0&-1\end{array}\right).\nonumber\]
- \(A\)tiene dos valores propios distintos\(\lambda_1,\lambda_2\). En este caso, uno tiene multiplicidad algebraica uno y el otro tiene multiplicidad algebraica dos; después de reordenar, podemos suponer que\(\lambda_1\) tiene multiplicidad\(1\) y\(\lambda_2\) tiene multiplicidad\(2\). Esto implica que\(\lambda_1\) tiene multiplicidad geométrica\(1\text{,}\) por lo que \(A\)es diagonalizable si y sólo si el\(\lambda_2\) -eigenspace es un plano. Por ejemplo:\[A=\left(\begin{array}{ccc}1&7&4\\0&2&0\\0&0&2\end{array}\right).\nonumber\] Por otro lado, si la multiplicidad geométrica de\(\lambda_2\) es\(1\text{,}\) entonces no\(A\) es diagonalizable. Por ejemplo:\[A=\left(\begin{array}{ccc}1&7&4\\0&2&1\\0&0&2\end{array}\right).\nonumber\]
- \(A\)tiene sólo un valor propio\(\lambda\). Si la multiplicidad algebraica de\(\lambda\) es\(1\text{,}\) entonces no\(A\) es diagonalizable. Esto sucede cuando el polinomio característico tiene dos raíces complejas (no reales). Por ejemplo:\[A=\left(\begin{array}{ccc}1&-1&0\\1&1&0\\0&0&2\end{array}\right).\nonumber\] De lo contrario, la multiplicidad algebraica de\(\lambda\) es igual a\(3\). En este caso, si la multiplicidad geométrica es\(1\text{:}\)\[A=\left(\begin{array}{ccc}1&1&1\\0&1&1\\0&0&1\end{array}\right)\nonumber\] o\(2\text{:}\)\[A=\left(\begin{array}{ccc}1&0&1\\0&1&1\\0&0&1\end{array}\right)\nonumber\] entonces no\(A\) es diagonalizable. Si la multiplicidad geométrica es\(3\text{,}\) entonces\(\text{Nul}(A-\lambda I_3) = \mathbb{R}^3 \text{,}\) así que\(A-\lambda I_3\) es la matriz cero, y por lo tanto\(A = \lambda I_3\). Por lo tanto, en este caso\(A\) es necesariamente diagonal, como en:\[A=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right).\nonumber\]
Similaridad y Multiplicidad
Recordemos de Fact 5.3.2 en la Sección 5.3 que matrices similares tienen los mismos valores propios. Resulta que ambas nociones de multiplicidad de un valor propio se conservan bajo similitud.
Dejar\(A\) y\(B\) ser\(n\times n\) matrices similares, y dejar\(\lambda\) ser un valor propio de\(A\) y\(B\). Entonces:
- La multiplicidad algebraica de\(\lambda\) es la misma para\(A\) y\(B\).
- La multiplicidad geométrica de\(\lambda\) es la misma para\(A\) y\(B\).
- Prueba
-
Dado que\(A\) y\(B\) tienen el mismo polinomio característico, la multiplicidad de\(\lambda\) como raíz del polinomio característico es la misma para ambas matrices, lo que prueba la primera afirmación. Para el segundo, supongamos que\(A = CBC^{-1}\) para una matriz invertible\(C\). Por Fact 5.3.3 en la Sección 5.3, la matriz\(C\) toma vectores propios de\(B\) vectores propios de\(A\text{,}\) ambos con autovalor\(\lambda\).
Dejemos\(\{v_1,v_2,\ldots,v_k\}\) ser una base del\(\lambda\) -propio espacio de\(B\). Afirmamos que\(\{Cv_1,Cv_2,\ldots,Cv_k\}\) es linealmente independiente. Supongamos que
\[ c_1Cv_1 + c_2Cv_2 + \cdots + c_kCv_k = 0. \nonumber \]
Reagrupamiento, esto significa
\[ C\bigl(c_1v_1 + c_2v_2 + \cdots + c_kv_k\bigr) = 0. \nonumber \]
Por Teorema 5.1.1 en la Sección 5.1, el espacio nulo de\(C\) es trivial, por lo que esto implica
\[ c_1v_1 + c_2v_2 + \cdots + c_kv_k = 0. \nonumber \]
Ya que\(v_1,v_2,\ldots,v_k\) son linealmente independientes, obtenemos\(c_1=c_2=\cdots=c_k=0\text{,}\) como se desee.
Por el párrafo anterior, la dimensión del\(\lambda\) -espacio propio de\(A\) es mayor o igual que la dimensión del\(\lambda\) -espacio propio de\(B\). Por simetría (\(A\)también\(B\) es similar a), las dimensiones son iguales, por lo que las multiplicidades geométricas coinciden.
Por ejemplo, las cuatro matrices en Ejemplo no\(\PageIndex{20}\) son similares entre sí, porque las multiplicidades algebraicas y/o geométricas de los valores propios no coinciden. O, combinado con el Teorema anterior\(\PageIndex{3}\), vemos que una matriz diagonalizable no puede ser similar a una no diagonalizable, porque las multiplicidades algebraicas y geométricas de tales matrices no pueden coincidir ambas.
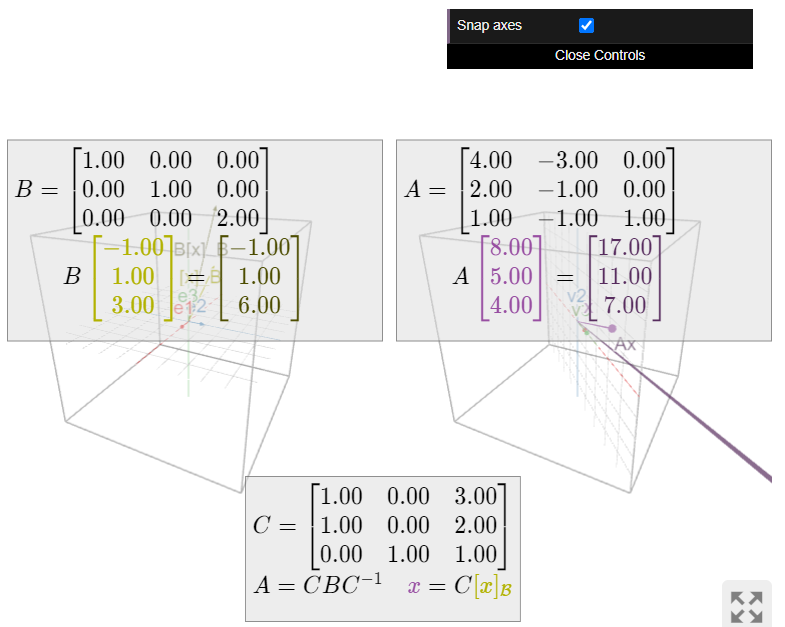
Continuando con este Ejemplo\(\PageIndex{8}\), vamos
\[ A = \left(\begin{array}{ccc}4&-3&0\\2&-1&0\\1&-1&1\end{array}\right). \nonumber \]
Esta es una matriz diagonalizable que es similar a
\[ D = \left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}\right)\quad\text{using the matrix}\quad C = \left(\begin{array}{ccc}1&0&3\\1&0&2\\0&1&1\end{array}\right). \nonumber \]
El\(1\) -espacio propio de\(D\) es el\(xy\) -plano, y el\(2\) -espacio propio es el\(z\) -eje. La matriz\(C\) toma el\(xy\) -plano al\(1\) -espacio propio del\(A\text{,}\) cual vuelve a ser un plano, y el\(z\) -eje al\(2\) -espacio propio del\(A\text{,}\) cual vuelve a ser una línea. Esto demuestra que las multiplicidades geométricas de\(A\) y\(D\) coinciden.
Lo contrario del Teorema\(\PageIndex{4}\) es falso: existen matrices cuyos vectores propios tienen las mismas multiplicidades algebraicas y geométricas, pero que no son similares. Ver Ejemplo\(\PageIndex{23}\) a continuación. Sin embargo, para\(2\times 2\) y\(3\times 3\) matrices cuyo polinomio característico no tiene raíces complejas (no reales), lo contrario del Teorema\(\PageIndex{4}\) es cierto. (Nos ocuparemos del caso de raíces complejas en la Sección 5.5.)
Demostrar que las matrices
\[A=\left(\begin{array}{cccc}0&0&0&0\\0&0&1&0\\0&0&0&1\\0&0&0&0\end{array}\right)\quad\text{and}\quad B=\left(\begin{array}{cccc}0&1&0&0\\0&0&0&0\\0&0&0&1\\0&0&0&0\end{array}\right)\nonumber\]
tienen los mismos valores propios con las mismas multiplicidades algebraicas y geométricas, pero no son similares.
Solución
Estas matrices son triangulares superiores. Ambos tienen polinomio característico\(f(\lambda) = \lambda^4\text{,}\) por lo que ambos tienen un valor propio\(0\) con multiplicidad algebraica\(4\). El\(0\) -eigenspace es el espacio nulo, Fact 5.1.2 en la Sección 5.1, que tiene dimensión\(2\) en cada caso porque\(A\) y\(B\) tienen dos columnas sin pivotes. De ahí\(0\) que tenga multiplicidad geométrica\(2\) en cada caso.
Para demostrar eso\(A\) y no\(B\) son similares, observamos que
\[A^2=\left(\begin{array}{cccc}0&0&0&0\\0&0&0&1\\0&0&0&0\\0&0&0&0\end{array}\right)\quad\text{and}\quad B^2=\left(\begin{array}{cccc}0&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{array}\right),\nonumber\]
como puede verificar el lector. Si\(A = CBC^{-1}\) entonces por Receta: Poderes de cómputos de una Matriz Diagonalizable, tenemos
\[ A^2 = CB^2C^{-1} = C0C^{-1} = 0, \nonumber \]
lo cual no es el caso.
Por otro lado, supongamos que\(A\) y\(B\) son matrices diagonalizables con el mismo polinomio característico. Dado que las multiplicidades geométricas de los valores propios coinciden con las multiplicidades algebraicas, que son las mismas para\(A\) y\(B\text{,}\) concluimos que existen vectores propios\(n\) linealmente independientes de cada matriz, todos los cuales tienen los mismos valores propios. Esto demuestra que\(A\) y ambos\(B\) son similares a la misma matriz diagonal. Usando la propiedad de transitividad, Proposición 5.3.1 en la Sección 5.3, de matrices similares, esto muestra:
Las matrices diagonalizables son similares si y sólo si tienen el mismo polinomio característico, o equivalentemente, los mismos valores propios con las mismas multiplicidades algebraicas.
Demostrar que las matrices
\[A=\left(\begin{array}{ccc}1&7&2\\0&-1&3\\0&0&4\end{array}\right)\quad\text{and}\quad B=\left(\begin{array}{ccc}1&0&0\\-2&4&0\\-5&-4&-1\end{array}\right)\nonumber\]
son similares.
Solución
Ambas matrices tienen los tres valores propios distintos\(1,-1,4\). De ahí que ambos sean diagonalizables, y son similares a la matriz diagonal
\[ \left(\begin{array}{ccc}1&0&0\\0&-1&0\\0&0&4\end{array}\right). \nonumber \]
Por la propiedad de transitividad, Proposición 5.3.1 en la Sección 5.3, de matrices similares, esto implica que\(A\) y\(B\) son similares entre sí.
Dos matrices diagonales cualesquiera con las mismas entradas diagonales (posiblemente en un orden diferente) son similares entre sí. En efecto, tales matrices tienen el mismo polinomio característico. Vimos este fenómeno en Ejemplo\(\PageIndex{5}\), donde señalamos que
\[\left(\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right)=\left(\begin{array}{ccc}0&0&1\\0&1&0\\1&0&0\end{array}\right)\left(\begin{array}{ccc}3&0&0\\0&2&0\\0&0&1\end{array}\right)\left(\begin{array}{ccc}0&0&1\\0&1&0\\1&0&0\end{array}\right)^{-1}.\nonumber\]


