5.5: Valores propios complejos
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Aprender a encontrar valores propios complejos y vectores propios de una matriz.
- Aprende a reconocer una matriz de escala de rotación y calcula según cuánto gira y escala la matriz.
- Comprender la geometría2×2 y3×3 las matrices con un valor propio complejo.
- Recetas: una2×2 matriz con un valor propio complejo es similar a una matriz de escala de rotación, el truco de autovector para2×2 matrices.
- Imágenes: la geometría de matrices con un valor propio complejo.
- Teoremas: el teorema de rotación-escalado, el teorema de diagonalización de bloques.
- Palabra de vocabulario: matriz de escala de rotación.
En la Sección 5.4, vimos que unan×n matriz cuyo polinomio característico tiene raíces realesn distintas es diagonalizable: es similar a una matriz diagonal, que es mucho más simple de analizar. La otra posibilidad es que una matriz tenga raíces complejas, y ese es el foco de esta sección. Resulta que tal matriz es similar (en el2×2 caso) a una matriz de escala de rotación, que también es relativamente fácil de entender.
En cierto sentido, toda esta sección es análoga a la Sección 5.4, con matrices de escala de rotación que juegan el papel de matrices diagonales. Consulte la Sección 7.1 para una revisión de los números complejos.
Matrices con valores propios complejos
Como consecuencia del teorema fundamental del álgebra, Teorema 7.1.1 en la Sección 7.1, aplicado al polinomio característico, vemos que:
Cadan×n matriz tiene valores propios exactamenten complejos, contados con multiplicidad.
Podemos calcular un vector propio correspondiente (complejo) exactamente de la misma manera que antes: por fila reduciendo la matrizA−λIn. Ahora, sin embargo, tenemos que hacer aritmética con números complejos.
Encuentra los valores propios complejos y los vectores propios de la matriz
A=(1−111).
Solución
El polinomio característico deA es
f(λ)=λ2−Tr(A)λ+det(A)=λ2−2λ+2.
Las raíces de este polinomio son
λ=2±√4−82=1±i.
Primero calculamos un vector propio paraλ=1+i. Tenemos
A−(1+i)I2=(1−(1+i)−111−(1+i))=(−i−11−i).
Ahora remaremos reducir, señalando que la segunda fila esi veces la primera:
(−i−11−i)R2=R2−iR1→(−i−100)R1=R1÷−i→(1−i00).
La forma paramétrica esx=iy, tal que un vector propio esv_1={i\choose 1}. A continuación calculamos un vector propio para\lambda=1-i. Tenemos
A-(1-i) I_2 = \left(\begin{array}{cc}1-(1-i)&-1\\1&1-(1-i)\end{array}\right) = \left(\begin{array}{cc}i&-1\\1&i\end{array}\right). \nonumber
Ahora remaremos reducir, señalando que la segunda fila es-i veces la primera:
\left(\begin{array}{cc}i&-1\\1&i\end{array}\right) \;\xrightarrow{R_2=R_2+iR_1}\; \left(\begin{array}{cc}i&-1\\0&0\end{array}\right) \;\xrightarrow{R_1=R_1\div i}\; \left(\begin{array}{cc}1&i\\0&0\end{array}\right). \nonumber
La forma paramétrica esx = -iy\text{,} tal que un vector propio esv_2 = {-i\choose 1}.
Podemos verificar nuestras respuestas:
\begin{aligned}\left(\begin{array}{cc}1&-1\\1&1\end{array}\right)\left(\begin{array}{c}i\\1\end{array}\right)&=\left(\begin{array}{c}i-1\\i+1\end{array}\right)=(1+i)\left(\begin{array}{c}i\\1\end{array}\right) \\ \left(\begin{array}{cc}1&-1\\1&1\end{array}\right)\left(\begin{array}{c}-i\\1\end{array}\right)&=\left(\begin{array}{c}-i-1\\-i+1\end{array}\right)=(1-i)\left(\begin{array}{c}-i\\1\end{array}\right).\end{aligned}
Encuentra los valores propios y vectores propios, reales y complejos, de la matriz
A=\left(\begin{array}{ccc}4/5&-3/5&0 \\ 3/5&4/5&0\\1&2&2\end{array}\right).\nonumber
Solución
Calculamos el polinomio característico expandiendo cofactores a lo largo de la tercera fila:
f(\lambda) = \det\left(\begin{array}{ccc}4/5-\lambda &-3/5&0 \\ 3/5&4-5-\lambda &0 \\ 1&2&2-\lambda\end{array}\right) = (2-\lambda)\left(\lambda^2-\frac 85\lambda+1\right). \nonumber
Este polinomio tiene una raíz real en2\text{,} y dos raíces complejas en
\lambda = \frac{8/5\pm\sqrt{64/25-4}}2 = \frac{4\pm 3i}5. \nonumber
Por lo tanto, los valores propios son
\lambda = 2,\quad \frac{4+3i}5,\quad \frac{4-3i}5. \nonumber
Nos globo ocular quev_1 = e_3 es un vector propio con valor propio2\text{,} ya que la tercera columna es2e_3.
A continuación encontramos un vector propio con valor propio(4+3i)/5. Tenemos
A-\frac{4+3i}5I_3 = \left(\begin{array}{ccc}-3i/5&-3/5&0\\3/5&-3i/5&0\\ 1&2&2-(4+3i)/5\end{array}\right) \;\xrightarrow[R_2=R_2\times5/3]{R_1=R_1\times -5/3}\; \left(\begin{array}{ccc}i&1&0\\1&-i&0\\1&2&\frac{6-3i}{5}\end{array}\right). \nonumber
Remamos reducir, señalando que la segunda fila es-i veces la primera:
\begin{aligned}\left(\begin{array}{ccc}i&1&0\\1&-i&0\\1&2&\frac{6-3i}{5}\end{array}\right)\xrightarrow{R_2=R_2+iR_1}\quad &\left(\begin{array}{ccc}i&1&0\\0&0&0\\1&2&\frac{6-3i}{5}\end{array}\right) \\ {}\xrightarrow{R_3=R_3+iR_1}\quad &\left(\begin{array}{ccc}i&1&0\\0&0&0\\0&2+i&\frac{6-3i}{5}\end{array}\right) \\ {}\xrightarrow{R_2\longleftrightarrow R_3}\quad &\left(\begin{array}{ccc}i&1&0\\0&2+i&\frac{6-3i}{5}\\0&0&0\end{array}\right) \\ {}\xrightarrow[R_2=R_2\div(2+i)]{R_1=R_1\div i}\quad &\left(\begin{array}{ccc}1&-i&0\\0&1&\frac{9-12i}{25}\\0&0&0\end{array}\right) \\ {}\xrightarrow{R_1=R_1+iR_2}\quad &\left(\begin{array}{ccc}1&0&\frac{12+9i}{25}\\0&1&\frac{9-12i}{25}\\0&0&0\end{array}\right).\end{aligned}
La variable libre esz\text{;} la forma paramétrica de la solución es
\left\{\begin{array}{rrr}x &=& -\dfrac{12+9i}{25}z \\ y &=& -\dfrac{9-12i}{25}z.\end{array}\right.\nonumber
Tomandoz=25 da el vector propio
v_2 = \left(\begin{array}{c}-12-9i\\-9+12i\\25\end{array}\right). \nonumber
Un cálculo similar (reemplazando todas las ocurrencias dei by-i) muestra que un vector propio con valor propio(4-3i)/5 es
v_3 = \left(\begin{array}{c}-12+9i\\-9-12i\\25\end{array}\right). \nonumber
Podemos verificar nuestros cálculos:
\begin{aligned}\left(\begin{array}{ccc}4/5&-3/5&0\\3/5&4/5&0\\1&2&2\end{array}\right)\left(\begin{array}{c}-12+9i\\-9-12i\\25\end{array}\right)&=\left(\begin{array}{c}-21/5+72i/5 \\ -72/5-21i/5\\20-15i\end{array}\right)=\frac{4+3i}{5}\left(\begin{array}{c}-12+9i\\-9-12i\\25\end{array}\right) \\ \left(\begin{array}{ccc}4/5&-3/5&0\\3/5&4/5&0\\1&2&2\end{array}\right)\left(\begin{array}{c}-12-9i\\-9+12i\\25\end{array}\right)&=\left(\begin{array}{c}-21/5-72i/5\\-72/5+21i/5\\20+15i\end{array}\right)=\frac{4-3i}{5}\left(\begin{array}{c}-12-9i\\-9+12i\\25\end{array}\right).\end{aligned}
SiA es una matriz con entradas reales, entonces su polinomio característico tiene coeficientes reales, por lo que la Nota 7.1.3 en la Sección 7.1 implica que sus valores propios complejos vienen en pares conjugados. En el primer ejemplo, notamos que
\begin{split} 1+i \text{ has an eigenvector } \amp v_1 =\left(\begin{array}{c}i\\1\end{array}\right) \\ 1-i \text{ has an eigenvector } \amp v_2 = \left(\begin{array}{c}-i\\1\end{array}\right). \end{split} \nonumber
En el segundo ejemplo,
\begin{split} \frac{4+3i}5 \text{ has an eigenvector } \amp v_1 = \left(\begin{array}{c}-12-9i\\-9+12i\\25\end{array}\right) \\ \frac{4-3i}5 \text{ has an eigenvector } \amp v_2 =\left(\begin{array}{c}-12+9i\\-9-12i\\25\end{array}\right) \end{split} \nonumber
En estos casos, un vector propio para el valor propio conjugado es simplemente el vector propio conjugado (el vector propio obtenido conjugando cada entrada del primer vector propio). Esto siempre es cierto. En efecto, siAv=\lambda v entonces
A \bar v = \bar{Av} = \bar{\lambda v} = \bar \lambda \bar v, \nonumber
que dice exactamente que\bar v es un vector propio deA con valor propio\bar \lambda.
DejarA ser una matriz con entradas reales. Si
\begin{split} \lambda \text{ is a complex eigenvalue with eigenvector } \amp v, \\ \text{then } \bar\lambda \text{ is a complex eigenvalue with eigenvector }\amp\bar v. \end{split} \nonumber
En otras palabras, tanto los valores propios como los vectores propios vienen en pares conjugados.
Dado que puede resultar tedioso dividir por números complejos mientras se reduce la fila, es útil aprender el siguiente truco, que funciona igualmente bien para matrices con entradas reales.
DejarA ser una2\times 2 matriz, y dejar\lambda ser un valor propio (real o complejo). Entonces
A - \lambda I_2 = \left(\begin{array}{cc}z&w\\ \star&\star\end{array}\right) \quad\implies\quad \left(\begin{array}{c}-w\\z\end{array}\right) \text{ is an eigenvector with eigenvalue } \lambda, \nonumber
asumiendo que la primera fila deA-\lambda I_2 es distinta de cero.
En efecto, como\lambda es un valor propio, sabemos que noA-\lambda I_2 es una matriz invertible. De ello se deduce que las filas son colineales (de lo contrario el determinante es distinto de cero), de manera que la segunda fila es automáticamente un múltiplo (complejo) de la primera:
\left(\begin{array}{cc}z&w\\ \star&\star\end{array}\right)=\left(\begin{array}{cc}z&w\\cz&cw\end{array}\right).\nonumber
Es obvio que{-w\choose z} está en el espacio nulo de esta matriz, como es{w\choose -z}\text{,} para el caso. Tenga en cuenta que nunca tuvimos que calcular la segunda fila de yA-\lambda I_2\text{,} mucho menos fila reducir!
Encuentra los valores propios complejos y los vectores propios de la matriz
A = \left(\begin{array}{cc}1&-1\\1&1\end{array}\right). \nonumber
Solución
Dado que el polinomio característico de una2\times 2 matrizA es quef(\lambda) = \lambda^2-\text{Tr}(A)\lambda + \det(A)\text{,} sus raíces son
\lambda = \frac{\text{Tr}(A)\pm\sqrt{\text{Tr}(A)^2-4\det(A)}}2 = \frac{2\pm\sqrt{4-8}}2 = 1\pm i. \nonumber
Para encontrar un vector propio con valor propio1+i\text{,} calculamos
A - (1+i)I_2 = \left(\begin{array}{cc}-i&-1\\ \star&\star\end{array}\right) \;\xrightarrow{\text{eigenvector}}\; v_1 = \left(\begin{array}{c}1\\-i\end{array}\right). \nonumber
El vector propio para el valor propio conjugado es el conjugado complejo:
v_2 = \bar v_1 = \left(\begin{array}{c}1\\i\end{array}\right). \nonumber
En Ejemplo\PageIndex{1} encontramos los vectores propios{i\choose 1} y{-i\choose 1} para los autovalores1+i y1-i\text{,} respectivamente, pero en Ejemplo\PageIndex{3} encontramos los vectores propios{1\choose -i} y{1\choose i} para los mismos valores propios de la misma matriz. Estos vectores no parecen múltiplos entre sí al principio, pero como ahora tenemos números complejos a nuestra disposición, podemos ver que en realidad son múltiplos:
-i\left(\begin{array}{c}i\\1\end{array}\right) = \left(\begin{array}{c}1\\-i\end{array}\right) \qquad i\left(\begin{array}{c}-i\\1\end{array}\right) = \left(\begin{array}{c}1\\i\end{array}\right). \nonumber
Matrices de escala de rotación
Los ejemplos más importantes de matrices con valores propios complejos son matrices de escala de rotación, es decir, múltiplos escalares de matrices de rotación.
Una matriz de escala de rotación es una2\times 2 matriz de la forma
\left(\begin{array}{cc}a&-b\\b&a\end{array}\right), \nonumber
dondea yb son números reales, no ambos iguales a cero.
La siguiente proposición justifica el nombre.
Dejar A = \left(\begin{array}{cc}a&-b\\b&a\end{array}\right) \nonumber ser una matriz de escala de rotación. Entonces:
- Aes un producto de una matriz de rotación\left(\begin{array}{cc}\cos\theta&-\sin\theta \\ \sin\theta&\cos\theta\end{array}\right)\quad\text{with a scaling matrix}\quad\left(\begin{array}{cc}r&0\\0&r\end{array}\right).\nonumber
- El factor de escalador es r = \sqrt{\det(A)} = \sqrt{a^2+b^2}. \nonumber
- El ángulo de rotación\theta es el ángulo en sentido contrario a las agujas del reloj desde elx eje positivo hasta el vector{a\choose b}\text{:}
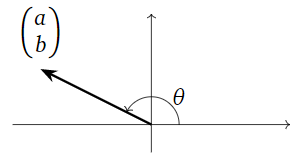
Figura\PageIndex{1}
Los valores propios deA son\lambda = a \pm bi.
- Prueba
-
Setr = \sqrt{\det(A)} = \sqrt{a^2+b^2}. El punto(a/r, b/r) tiene la propiedad que
\left(\frac ar\right)^2 + \left(\frac br\right)^2 = \frac{a^2+b^2}{r^2} = 1. \nonumber
En otras palabras,(a/r,b/r) se encuentra en el círculo unitario. Por lo tanto, tiene la forma(\cos\theta,\sin\theta)\text{,} donde\theta está el ángulo en sentido antihorario desde elx eje positivo hasta el vector{a/r\choose b/r}\text{,} o ya que está en la misma línea, para{a\choose b}\text{:}
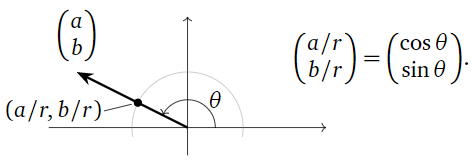
Figura\PageIndex{2}
De ello se deduce que
A = r\left(\begin{array}{cc}a/r&-b/r \\ b/r&a/r\end{array}\right) =\left(\begin{array}{cc}r&0\\0&r\end{array}\right) \left(\begin{array}{cc}\cos\theta&-\sin\theta \\ \sin\theta&\cos\theta\end{array}\right), \nonumber
según se desee.
Para la última declaración, calculamos los valores propios deA como las raíces del polinomio característico:
\lambda = \frac{\text{Tr}(A)\pm\sqrt{\text{Tr}(A)^2-4\det(A)}}2 = \frac{2a\pm\sqrt{4a^2-4(a^2+b^2)}}2 = a\pm bi. \nonumber
Geométricamente, una matriz de escala de rotación hace exactamente lo que dice el nombre: gira y escala (en cualquier orden).
Qué hace la matriz
A = \left(\begin{array}{cc}1&-1\\1&1\end{array}\right) \nonumber
hacer geométricamente?
Solución
Esta es una matriz de escala de rotación cona=b=1. Por lo tanto, se escala en un factor de\sqrt{\det(A)} = \sqrt 2 y gira en sentido antihorario por45^\circ\text{:}
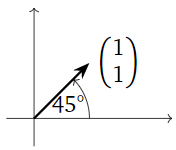
Figura\PageIndex{3}
Aquí hay una foto deA\text{:}
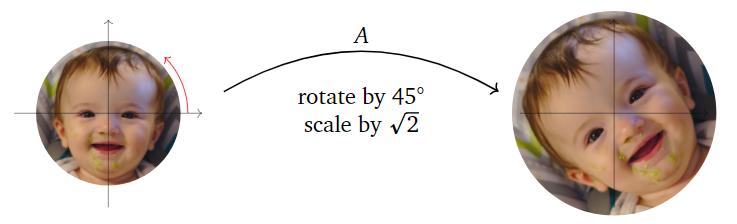
Figura\PageIndex{4}
A continuación se incluye una figura interactiva.

Qué hace la matriz
A = \left(\begin{array}{cc}-\sqrt{3}&-1\\1&-\sqrt{3}\end{array}\right) \nonumber
hacer geométricamente?
Solución
Esta es una matriz de escala de rotación cona=-\sqrt3 yb=1. Por lo tanto, se escala en un factor de\sqrt{\det(A)}=\sqrt{3+1}=2 y gira en sentido contrario a las agujas del reloj por el ángulo\theta en la imagen:
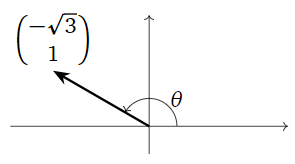
Figura\PageIndex{6}
Para calcular este ángulo, hacemos un poco de trigonometría:
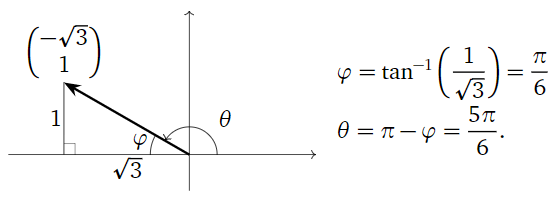
Figura\PageIndex{7}
Por lo tanto,A gira en sentido antihorario5\pi/6 y escala por un factor de2.
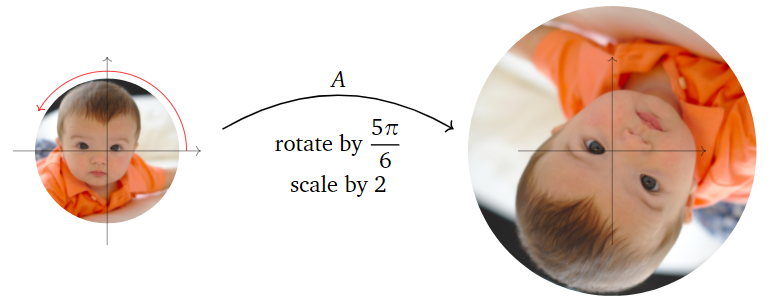
Figura\PageIndex{8}
A continuación se incluye una figura interactiva.

La matriz en el segundo ejemplo tiene una segunda columna{-\sqrt 3\choose 1}\text{,} que se gira en sentido contrario a las agujas del reloj desde elx eje positivo en un ángulo de5\pi/6. Este ángulo de rotación no es igual a\tan^{-1}\bigl(1/(-\sqrt3)\bigr) = -\frac\pi 6. El problema es que arctan siempre genera valores entre-\pi/2 y\pi/2\text{:} no da cuenta de puntos en el segundo o tercer cuadrantes. Es por eso que dibujamos un triángulo y usamos sus longitudes de borde (positivas) para calcular el ángulo\varphi\text{:}
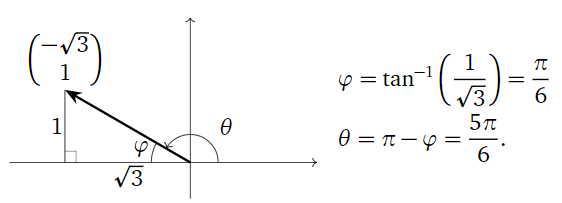
Figura\PageIndex{10}
Alternativamente, podríamos haber observado que se{-\sqrt 3\choose 1} encuentra en el segundo cuadrante, de manera que el ángulo\theta en cuestión es
\theta = \tan^{-1}\left(\frac1{-\sqrt3}\right) + \pi. \nonumber
Al encontrar el ángulo de rotación de un vector{a\choose b}\text{,} no compute ciegamente\tan^{-1}(b/a)\text{,} ya que esto dará la respuesta incorrecta cuando{a\choose b} esté en el segundo o tercer cuadrante. En cambio, dibuja un cuadro.
Geometría de2 \times 2 Matrices con un Valor propio Complejo
DejarA ser una2\times 2 matriz con un valor propio complejo, no real\lambda. EntoncesA también tiene el valor propio\bar\lambda\neq\lambda. En particular,A tiene valores propios distintos, por lo que es diagonalizable usando los números complejos. A menudo nos gusta pensar en nuestras matrices como una descripción de transformaciones de\mathbb{R}^n (en contraposición a\mathbb{C}^n). Debido a esto, la siguiente construcción es útil. Da algo así como una diagonalización, excepto que todas las matrices involucradas tienen entradas reales.
DejarA ser una matriz2\times 2 real con un valor propio complejo (no real)\lambda\text{,} y dejarv ser un vector propio. EntoncesA = CBC^{-1} para
C = \left(\begin{array}{cc}|&| \\ \Re (v)&\Im(v) \\ |&|\end{array}\right)\quad\text{and}\quad B = \left(\begin{array}{cc}\Re(\lambda)&\Im(\lambda) \\ -\Im(\lambda)&\Re(\lambda)\end{array}\right). \nonumber
En particular,A es similar a una matriz de escala de rotación que escala por un factor de|\lambda| = \sqrt{\det(B)}.
- Prueba
-
Primero tenemos que demostrar eso\Re(v) y\Im(v) somos linealmente independientes, ya que de lo contrario noC es invertible. Si no, entonces existen números realesx,y, no ambos iguales a cero, tal quex\Re(v) + y\Im(v) = 0. Entonces
\begin{split} (y+ix)v \amp= (y+ix)\bigl(\Re(v)+i\Im(v)\bigr) \\ \amp= y\Re(v) - x\Im(v) + \left(x\Re(v) + y\Im(v)\right)i \\ \amp= y\Re(v) - x\Im(v). \end{split} \nonumber
Ahora, también(y+ix)v es un vector propio deA con valor propio\lambda\text{,} ya que es un múltiplo escalar dev. Pero acabamos de demostrar que(y+ix)v es un vector con entradas reales, y cualquier vector propio real de una matriz real tiene un valor propio real. Por lo tanto,\Re(v) y\Im(v) debe ser linealmente independiente después de todo.
Dejar\lambda = a+bi yv = {x+yi\choose z+wi}. Observamos que
\begin{split} Av = \lambda v \amp= (a+bi)\left(\begin{array}{c}x+yi\\z+wi\end{array}\right) \\ \amp= \left(\begin{array}{c}(ax-by)+(ay+bx)i \\ (az-bw)+(aw+bz)i\end{array}\right) \\ \amp= \left(\begin{array}{c}ax-by\\az-bw\end{array}\right) + i\left(\begin{array}{c}ay+bx \\ aw+bz\end{array}\right). \end{split} \nonumber
Por otro lado, tenemos
A\left(\left(\begin{array}{c}x\\z\end{array}\right) + i\left(\begin{array}{c}y\\w\end{array}\right)\right) = A\left(\begin{array}{c}x\\z\end{array}\right) + iA\left(\begin{array}{c}y\\w\end{array}\right) = A\Re(v) + iA\Im(v). \nonumber
Emparejar partes reales e imaginarias da
A\Re(v) = \left(\begin{array}{c}ax-by\\az-bw\end{array}\right) \qquad A\Im(v) = \left(\begin{array}{c}ay+bx\\aw+bz\end{array}\right). \nonumber
Ahora calculamosCBC^{-1}\Re(v) yCBC^{-1}\Im(v). DesdeCe_1 = \Re(v) yCe_2 = \Im(v)\text{,} tenemosC^{-1}\Re(v) = e_1 yC^{-1}\Im(v)=e_2\text{,} así
\begin{split} CBC^{-1}\Re(v) \amp= CBe_1 = C\left(\begin{array}{c}a\\-b\end{array}\right) = a\Re(v)-b\Im(v) \\ \amp= a\left(\begin{array}{c}x\\z\end{array}\right) - b\left(\begin{array}{c}y\\w\end{array}\right) =\left(\begin{array}{c}ax-by\\az-bw\end{array}\right) = A\Re(v) \\ CBC^{-1}\Im(v) \amp= CBe_2 = C\left(\begin{array}{c}b\\a\end{array}\right) = b\Re(v)+a\Im(v) \\ \amp= b\left(\begin{array}{c}x\\z\end{array}\right) + a\left(\begin{array}{c}y\\w\end{array}\right) = \left(\begin{array}{c}ay+bx\\aw+bz\end{array}\right) = A\Im(v). \end{split} \nonumber
Por lo tanto,A\Re(v) = CBC^{-1}\Re(v) yA\Im(v) = CBC^{-1}\Im(v).
Dado que\Re(v) y\Im(v) son linealmente independientes, forman una base para\mathbb{R}^2 . Dejarw ser cualquier vector en\mathbb{R}^2 \text{,} y escribirw = c\Re(v) + d\Im(v). Entonces
\begin{split} Aw \amp= A\bigl(c\Re(v) + d\Im(v)\bigr) \\ \amp= cA\Re(v) + dA\Im(v) \\ \amp= cCBC^{-1}\Re(v) + dCBC^{-1}\Im(v) \\ \amp= CBC^{-1}\bigl(c\Re(v) + d\Im(v)\bigr) \\ \amp= CBC^{-1} w. \end{split} \nonumber
Esto lo demuestraA = CBC^{-1}.
Aquí\Re y\Im denotan las partes reales e imaginarias, respectivamente:
\Re(a+bi) = a \quad \Im(a+bi) = b \quad \Re\left(\begin{array}{c}x+yi\\z+wi\end{array}\right) = \left(\begin{array}{c}x\\z\end{array}\right) \quad \Im\left(\begin{array}{c}x+yi\\z+wi\end{array}\right) = \left(\begin{array}{c}y\\w\end{array}\right). \nonumber
La matriz de escala de rotación en cuestión es la matriz
B = \left(\begin{array}{cc}a&-b\\b&a\end{array}\right)\quad\text{with}\quad a = \Re(\lambda),\; b = -\Im(\lambda). \nonumber
Geométricamente, el teorema de escala de rotación dice que una2\times 2 matriz con un valor propio complejo se comporta de manera similar a una matriz de escala de rotación. Ver Nota 5.3.3 en la Sección 5.3.
Se debe considerar el Teorema\PageIndex{1} como un análogo cercano del Teorema 5.4.1 en la Sección 5.4, con una matriz de escala de rotación que juega el papel de una matriz diagonal. Antes de continuar, replanteamos el teorema como receta:
ADéjese ser una matriz2\times 2 real.
- Calcular el polinomio característico y f(\lambda) = \lambda^2 - \text{Tr}(A)\lambda + \det(A), \nonumber luego computar sus raíces usando la fórmula cuadrática.
- Si los valores propios son complejos, elige uno de ellos, y llámenlo\lambda.
- Encuentra un valor propio correspondiente (complejo)v usando el truco 3.
- EntoncesA=CBC^{-1} para C = \left(\begin{array}{cc}|&| \\ \Re(v)&\Im(v) \\ |&|\end{array}\right)\quad\text{and}\quad B = \left(\begin{array}{cc}\Re(\lambda)&\Im(\lambda) \\ -\Im(\lambda)&\Re(\lambda)\end{array}\right). \nonumber Esta escala por un factor de|\lambda|.
Qué hace la matriz
A = \left(\begin{array}{cc}2&-1\\2&0\end{array}\right) \nonumber
hacer geométricamente?
Solución
Los valores propios deA son
\lambda = \frac{\text{Tr}(A) \pm \sqrt{\text{Tr}(A)^2-4\det(A)}}2 = \frac{2\pm\sqrt{4-8}}2 = 1\pm i. \nonumber
Elegimos el valor propio\lambda = 1-i y encontramos un vector propio correspondiente, usando el truco, tenga en cuenta\PageIndex{3}:
A - (1-i)I_2 = \left(\begin{array}{cc}1+i&-1 \\ \star&\star\end{array}\right) \;\xrightarrow{\text{eigenvector}}\; v = \left(\begin{array}{c}1\\1+i\end{array}\right). \nonumber
Según el teorema\PageIndex{1}, tenemosA=CBC^{-1} para
\begin{split} C \amp= \left(\begin{array}{cc}\Re\left(\begin{array}{c}1\\1+i\end{array}\right)&\Im\left(\begin{array}{c}1\\1+i\end{array}\right)\end{array}\right) = \left(\begin{array}{cc}1&0\\1&1\end{array}\right) \\ B \amp= \left(\begin{array}{cc}\Re(\lambda)&\Im(\lambda) \\ -\Im(\lambda)&\Re(\lambda)\end{array}\right) = \left(\begin{array}{cc}1&-1\\1&1\end{array}\right). \end{split} \nonumber
La matrizB es la matriz de escala de rotación anterior Ejemplo\PageIndex{4}: gira en sentido antihorario por un ángulo de45^\circ y escala por un factor de\sqrt 2. La matrizA hace lo mismo, pero con respecto al sistema\Re(v),\Im(v) -coordinate:
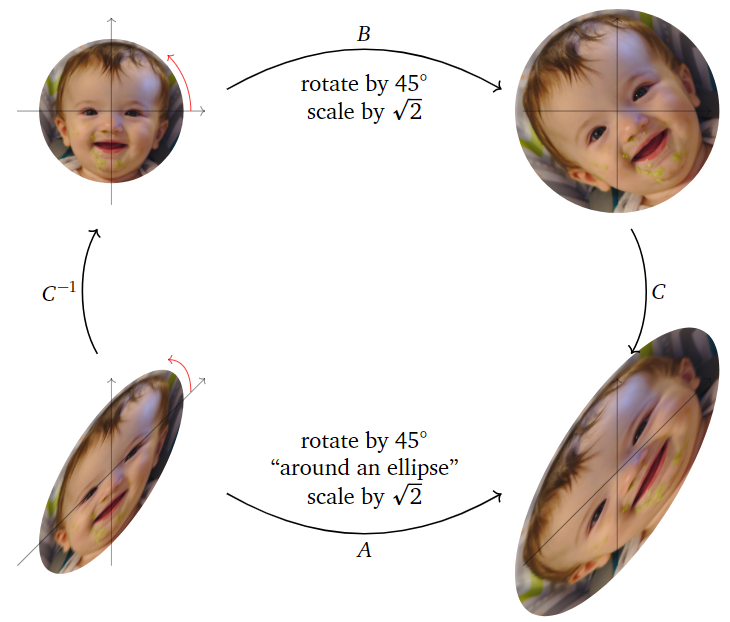
Figura\PageIndex{11}
Para resumir:
- Bgira alrededor del círculo centrado en el origen y que pasa a travése_1 ye_2\text{,} en la dirección dee_1 ae_2\text{,} entonces escala por\sqrt 2.
- Agira alrededor de la elipse centrada en el origen y pasando a través\Re(v) y\Im(v)\text{,} en la dirección desde\Re(v) hasta\Im(v)\text{,} entonces escala por\sqrt 2.
El lector podría querer volver a referirse al Ejemplo 5.3.7 en la Sección 5.3.
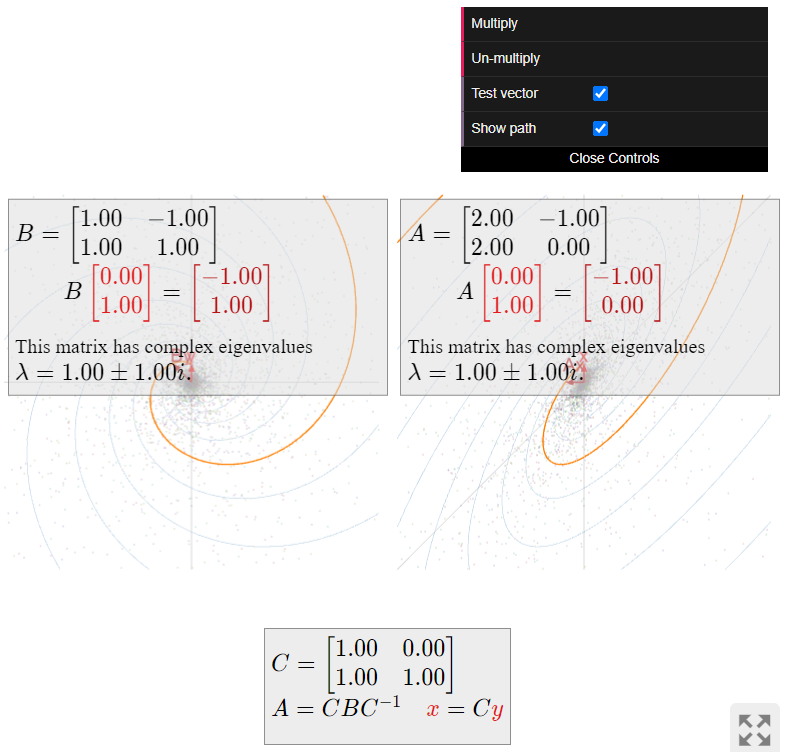
Si en cambio hubiéramos elegido\bar\lambda = 1+i como nuestro valor propio, entonces habríamos encontrado el vector propio\bar v = {1\choose 1-i}. En este caso tendríamosA=C'B'(C')^{-1}\text{,} donde
\begin{split} C' \amp= \left(\begin{array}{cc}\Re\left(\begin{array}{c}1\\1-i\end{array}\right)&\Im\left(\begin{array}{c}1\\1-i\end{array}\right)\end{array}\right) = \left(\begin{array}{cc}1&0\\1&-1\end{array}\right) \\ B' \amp= \left(\begin{array}{cc}\Re(\overline{\lambda})&\Im(\overline{\lambda}) \\ -\Im(\overline{\lambda})&\Re(\overline{\lambda})\end{array}\right) = \left(\begin{array}{cc}1&1\\-1&1\end{array}\right). \end{split} \nonumber
Entonces, tambiénA es similar a una rotación en sentido horario por45^\circ\text{,} seguida de una escala por\sqrt 2.
Qué hace la matriz
A = \left(\begin{array}{cc}-\sqrt{3}+1&-2\\1&-\sqrt{3}-1\end{array}\right) \nonumber
hacer geométricamente?
Solución
Los valores propios deA son
\lambda = \frac{\text{Tr}(A) \pm \sqrt{\text{Tr}(A)^2-4\det(A)}}2 = \frac{-2\sqrt 3\pm\sqrt{12-16}}2 = -\sqrt3\pm i. \nonumber
Elegimos el valor propio\lambda = -\sqrt3-i y encontramos un vector propio correspondiente, usando el truco, tenga en cuenta\PageIndex{3}:
A - (-\sqrt3-i)I_2 = \left(\begin{array}{cc}1+i&-2\\ \star&\star\end{array}\right) \;\xrightarrow{\text{eigenvector}}\; v = \left(\begin{array}{c}2\\1+i\end{array}\right). \nonumber
Según el teorema\PageIndex{1}, tenemosA=CBC^{-1} para
\begin{split} C \amp= \left(\begin{array}{cc}\Re\left(\begin{array}{c}2\\1+i\end{array}\right)&\Im\left(\begin{array}{c}2\\1+i\end{array}\right)\end{array}\right) = \left(\begin{array}{cc}2&0\\1&1\end{array}\right) \\ B \amp= \left(\begin{array}{cc}\Re(\lambda)&\Im(\lambda) \\ -\Im(\lambda)&\Re(\lambda)\end{array}\right) = \left(\begin{array}{cc}-\sqrt{3}&-1\\1&-\sqrt{3}\end{array}\right). \end{split} \nonumber
La matrizB es la matriz de escala de rotación en el Ejemplo anterior\PageIndex{5}: gira en sentido antihorario por un ángulo de5\pi/6 y escala por un factor de2. La matrizA hace lo mismo, pero con respecto al sistema\Re(v),\Im(v) -coordinate:
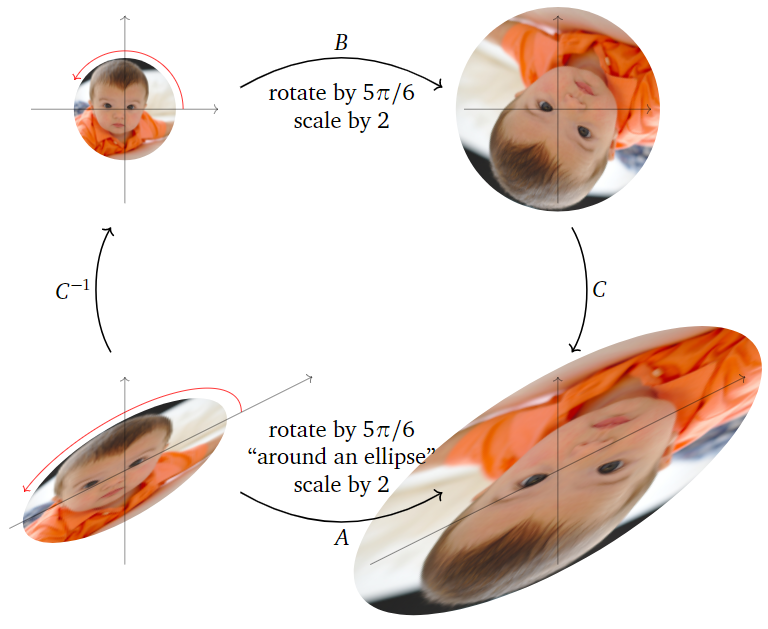
Figura\PageIndex{13}
Para resumir:
- Bgira alrededor del círculo centrado en el origen y que pasa a travése_1 ye_2\text{,} en la dirección dee_1 ae_2\text{,} entonces escala por2.
- Agira alrededor de la elipse centrada en el origen y pasando a través\Re(v) y\Im(v)\text{,} en la dirección desde\Re(v) hasta\Im(v)\text{,} entonces escala por2.
El lector podría querer volver a referirse al Ejemplo 5.3.7 en la Sección 5.3.
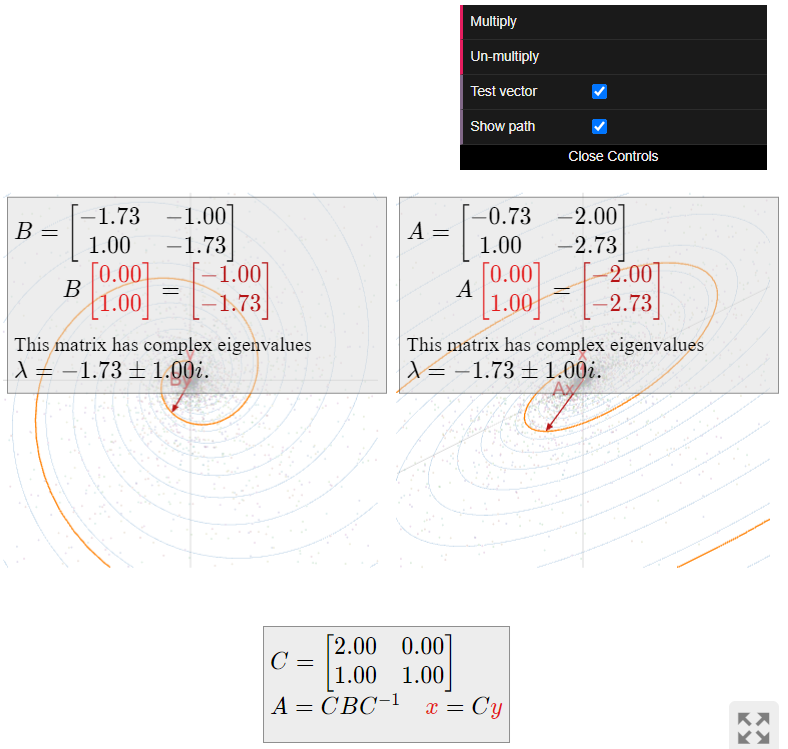
Si en cambio hubiéramos elegido\bar\lambda = -\sqrt3-i como nuestro valor propio, entonces habríamos encontrado el vector propio\bar v = {2\choose 1-i}. En este caso tendríamosA=C'B'(C')^{-1}\text{,} donde
\begin{split} C' \amp= \left(\begin{array}{cc}\Re\left(\begin{array}{c}2\\1-i\end{array}\right)&\Im\left(\begin{array}{c}2\\1-i\end{array}\right)\end{array}\right) = \left(\begin{array}{cc}2&0\\1&-1\end{array}\right) \\ B' \amp= \left(\begin{array}{cc}\Re(\overline{\lambda})&\Im(\overline{\lambda}) \\ -\Im(\overline{\lambda})&\Re(\overline{\lambda})\end{array}\right) = \left(\begin{array}{cc}-\sqrt{3}&1\\-1&-\sqrt{3}\end{array}\right). \end{split} \nonumber
Entonces, tambiénA es similar a una rotación en sentido horario por5\pi/6\text{,} seguida de una escala por2.
Vimos en los ejemplos anteriores que el Teorema se\PageIndex{1} puede aplicar de dos maneras diferentes a cualquier matriz dada: uno tiene que elegir uno de los dos valores propios conjugados con los que trabajar. Reemplazar\lambda por\bar\lambda tiene el efecto de reemplazarv por\bar v\text{,} lo que solo niega todas las partes imaginarias, así que también tenemosA=C'B'(C')^{-1} para
C' = \left(\begin{array}{cc}|&| \\ \Re(v)&-\Im(v) \\ |&|\end{array}\right)\quad\text{and}\quad B' = \left(\begin{array}{cc}\Re(\lambda)&-\Im(\lambda) \\ \Im(\lambda)&\Re(\lambda)\end{array}\right). \nonumber
Las matricesB yB' son similares entre sí. La única diferencia entre ellos es el sentido de rotación, ya que{\Re(\lambda)\choose -\Im(\lambda)} y{\Re(\lambda)\choose \Im(\lambda)} son imágenes especulares entre sí sobre elx eje -eje:
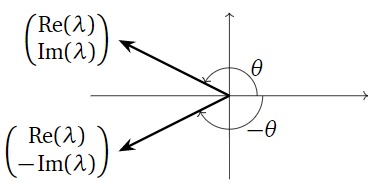
Figura\PageIndex{15}
La discusión que sigue es muy análoga a la exposición en la subsección La geometría de las matrices diagonalizables en la Sección 5.4, en la que se estudió la dinámica de2\times 2 las matrices diagonalizables.
DejarA ser una2\times 2 matriz con un valor propio complejo (no real)\lambda. Por Teorema\PageIndex{1}, la matrizA es similar a una matriz que gira en cierta cantidad y escala por|\lambda|. De ahí,A gira alrededor de una elipse y escala por|\lambda|. Hay tres casos diferentes.
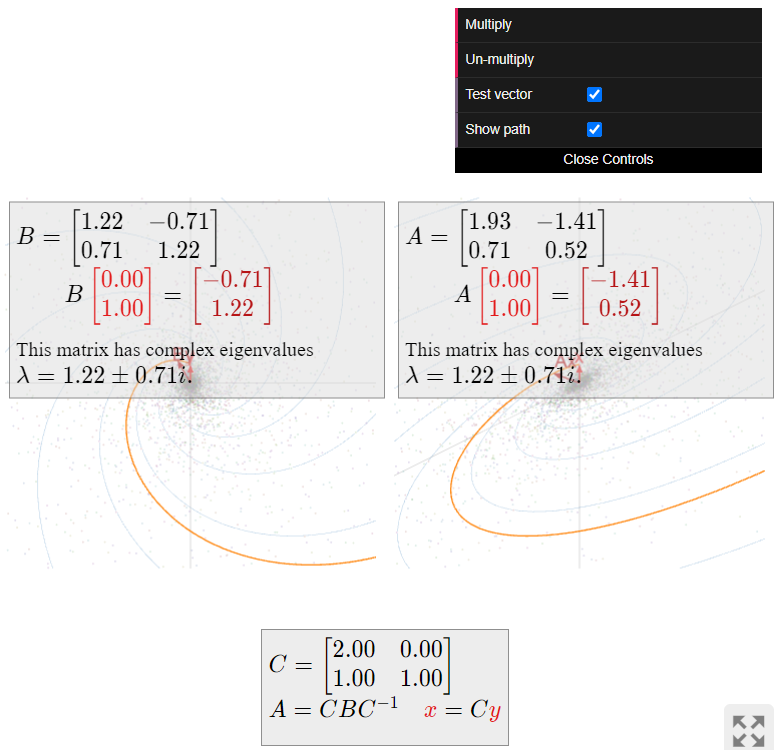
\color{Red}|\lambda| > 1\text{:}cuando el factor de escalado es mayor que1\text{,} entonces los vectores tienden a alargarse, es decir, más lejos del origen. En este caso, multiplicar repetidamente un vector porA hace que el vector se “salga en espiral”. Por ejemplo,
A = \frac 1{\sqrt 2}\left(\begin{array}{cc}\sqrt{3}+1&-2\\1&\sqrt{3}-1\end{array}\right) \qquad \lambda = \frac{\sqrt3-i}{\sqrt 2} \qquad |\lambda| = \sqrt 2 > 1 \nonumber
da lugar a la siguiente imagen:
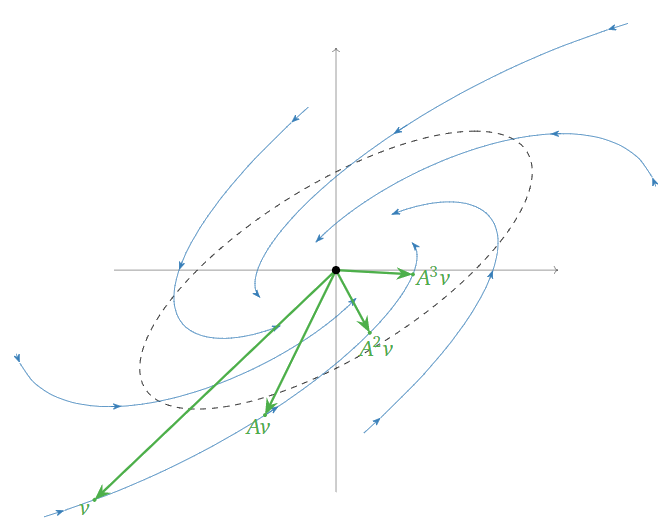
Figura\PageIndex{16}
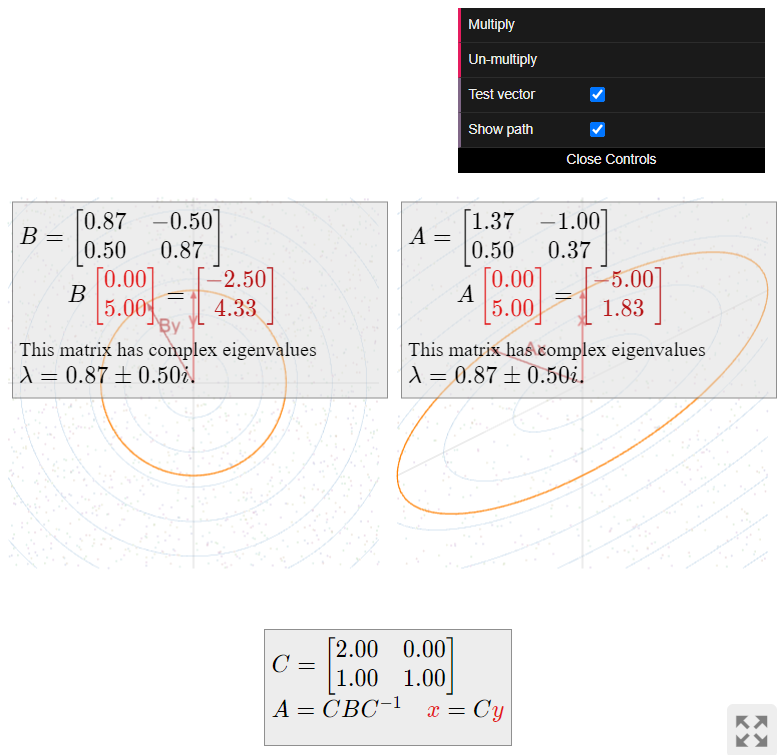
\color{Red}|\lambda| = 1\text{:}cuando el factor de escalado es igual a1\text{,} entonces los vectores no tienden a alargarse o acortarse. En este caso, multiplicar repetidamente un vector porA simplemente “gira alrededor de una elipse”. Por ejemplo,
A = \frac 12\left(\begin{array}{cc}\sqrt{3}+1&-2\\1&\sqrt{3}-1\end{array}\right) \qquad \lambda = \frac{\sqrt3-i}2 \qquad |\lambda| = 1 \nonumber
da lugar a la siguiente imagen:
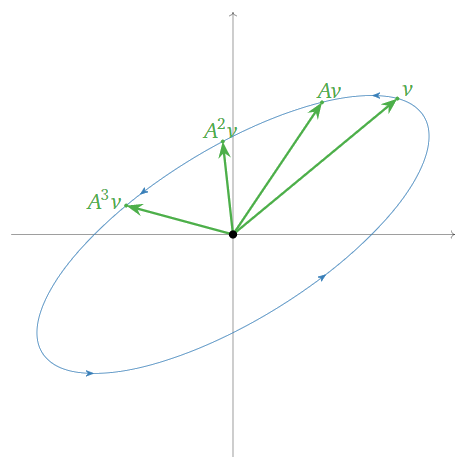
Figura\PageIndex{17}
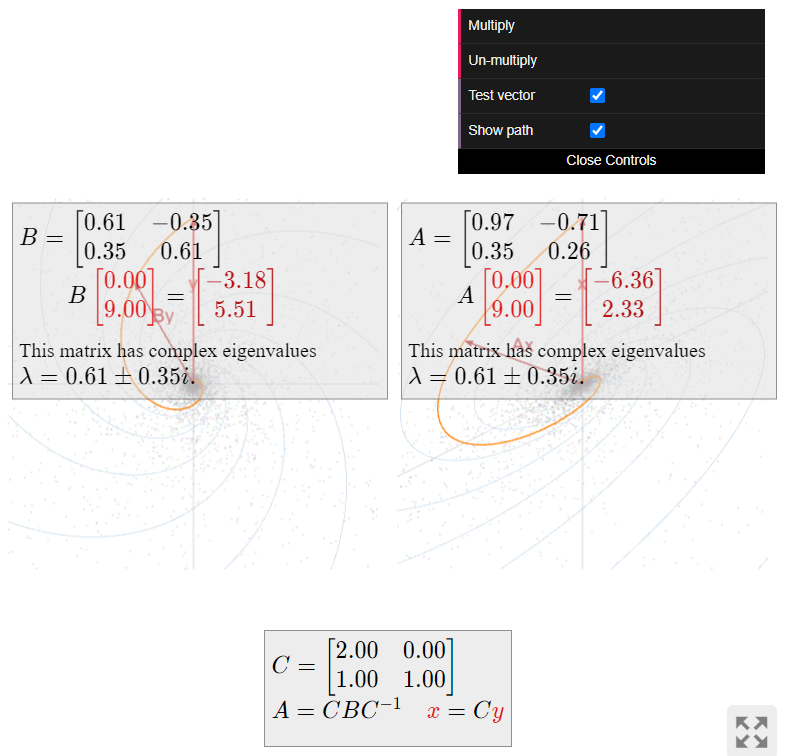
\color{Red}|\lambda| \lt 1\text{:}cuando el factor de escalado es menor que1\text{,} entonces los vectores tienden a acortarse, es decir, más cerca del origen. En este caso, multiplicar repetidamente un vector porA hace que el vector se “incline”. Por ejemplo,
A = \frac 1{2\sqrt 2}\left(\begin{array}{cc}\sqrt{3}+1&-2\\1&\sqrt{3}-1\end{array}\right) \qquad \lambda = \frac{\sqrt3-i}{2\sqrt 2} \qquad |\lambda| = \frac 1{\sqrt 2} \lt 1 \nonumber
da lugar a la siguiente imagen:

Figura\PageIndex{18}
A = \frac 1{\sqrt 2}\left(\begin{array}{cc}\sqrt{3}+1&-2\\1&\sqrt{3}-1\end{array}\right) \qquad B = \frac 1{\sqrt 2}\left(\begin{array}{cc}\sqrt{3}&-1\\1&\sqrt{3}\end{array}\right) \qquad C = \left(\begin{array}{cc}2&0\\1&1\end{array}\right) \nonumber
\lambda = \frac{\sqrt3-i}{\sqrt 2} \qquad |\lambda| = \sqrt 2 > 1 \nonumber
A = \frac 12\left(\begin{array}{cc}\sqrt{3}+1&-2\\1&\sqrt{3}-1\end{array}\right) \qquad B = \frac 12\left(\begin{array}{cc}\sqrt{3}&-1\\1&\sqrt{3}\end{array}\right) \qquad C = \left(\begin{array}{cc}2&0\\1&1\end{array}\right) \nonumber
\lambda = \frac{\sqrt3-i}2 \qquad |\lambda| = 1 \nonumber
A = \frac 1{2\sqrt 2}\left(\begin{array}{cc}\sqrt{3}+1&-2\\1&\sqrt{3}-1\end{array}\right) \qquad B = \frac 1{2\sqrt 2}\left(\begin{array}{cc}\sqrt{3}&-1\\1&\sqrt{3}\end{array}\right) \qquad C = \left(\begin{array}{cc}2&0\\1&1\end{array}\right) \nonumber
\lambda = \frac{\sqrt3-i}{2\sqrt 2} \qquad |\lambda| = \frac 1{\sqrt 2} \lt 1 \nonumber
En este punto, podemos anotar la matriz “más simple” posible que es similar a cualquier2\times 2 matriz dadaA. Hay cuatro casos:
- Atiene dos valores propios reales\lambda_1,\lambda_2. En este caso,A es diagonalizable, por lo queA es similar a la matriz \left(\begin{array}{cc}\lambda_1&0\\0&\lambda_2\end{array}\right). \nonumber Esta representación es única hasta reordenar los valores propios.
- Atiene un valor propio real\lambda de multiplicidad geométrica2. En este caso, vimos en el Ejemplo 5.4.20 en la Sección 5.4 queA es igual a la matriz \left(\begin{array}{cc}\lambda&0\\0&\lambda\end{array}\right). \nonumber
- Atiene un valor propio real\lambda de multiplicidad geométrica1. En este caso, noA es diagonalizable, y vimos en Observación:2\times 2 Matrices no diagonalizables con un valor propio en la Sección 5.4 queA es similar a la matriz \left(\begin{array}{cc}\lambda&1\\0&\lambda\end{array}\right). \nonumber
- Ano tiene valores propios reales. En este caso,A tiene un valor propio complejo\lambda\text{,} yA es similar a la matriz rotación-escalado \left(\begin{array}{cc}\Re(\lambda)&\Im(\lambda) \\ -\Im(\lambda)&\Re(\lambda)\end{array}\right) \nonumber por Teorema\PageIndex{1}. Por Proposición\PageIndex{1}, los valores propios de una matriz de escala de rotación de\left(\begin{array}{cc}a&-b\\b&a\end{array}\right) are \(a\pm bi\text{,} manera que dos matrices de escala de rotación\left(\begin{array}{cc}a&-b\\b&a\end{array}\right) y\left(\begin{array}{cc}c&-d\\d&c\end{array}\right) son similares si y solo sia=c yb=\pm d.
Diagonalización de bloques
Para matrices mayores que2\times 2\text{,} hay un teorema que combina el Teorema 5.4.1 en la Sección 5.4 y el Teorema\PageIndex{1}. Dice esencialmente que una matriz es similar a una matriz con partes que parecen una matriz diagonal, y partes que parecen una matriz de escala de rotación.
ADéjese ser unan\times n matriz real. Supongamos que para cada valor propio (real o complejo), la multiplicidad algebraica es igual a la multiplicidad geométrica. EntoncesA = CBC^{-1}\text{,} dondeB yC son los siguientes:
- La matrizB es diagonal de bloques, donde los bloques son1\times 1 bloques que contienen los valores propios reales (con sus multiplicidades), o2\times 2 bloques que contienen las matrices \left(\begin{array}{cc}\Re(\lambda)&\Im(\lambda) \\ -\Im(\lambda)&\Re(\lambda)\end{array}\right) \nonumber para cada valor propio no real\lambda (con multiplicidad).
- Las columnas deC forman bases para los espacios propios para los vectores propios reales, o vienen en pares\bigl(\,\Re(v)\;\Im(v)\,\bigr) para los vectores propios no reales.
El Teorema\PageIndex{2} se demuestra de la misma manera que el Teorema 5.4.1 en la Sección 5.4 y Teorema\PageIndex{1}. Se entiende mejor en el caso de3\times 3 las matrices.
DejarA ser una3\times 3 matriz con un valor propio complejo\lambda_1. Entonces\bar\lambda_1 hay otro valor propio, y hay un valor propio real\lambda_2. Dado que hay tres valores propios distintos, tienen multiplicidad algebraica y geométrica uno, por lo que el Teorema\PageIndex{2} se aplica aA.
Dejarv_1 ser un vector propio (complejo) con valor propio\lambda_1\text{,} y dejarv_2 ser un vector propio (real) con valor propio\lambda_2. Entonces el teorema\PageIndex{2} dice queA = CBC^{-1} para
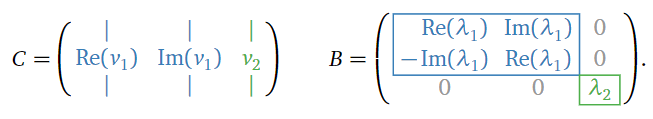
Figura\PageIndex{22}
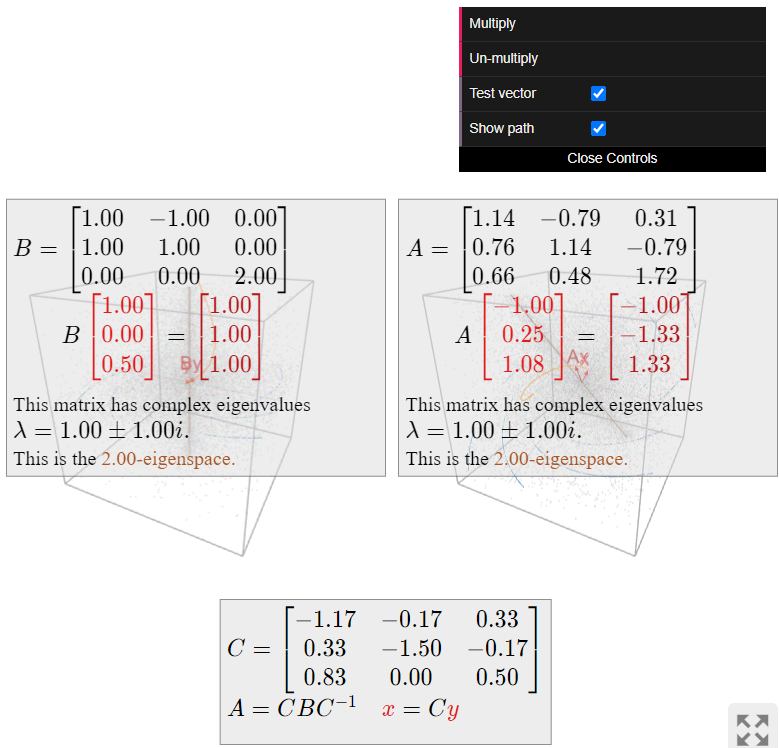
Qué hace la matriz
A = \frac 1{29}\left(\begin{array}{ccc}33&-23&9\\22&33&-23\\19&14&50\end{array}\right) \nonumber
hacer geométricamente?
Solución
Primero encontramos los valores propios (reales y complejos) deA. Calculamos el polinomio característico usando cualquier método que nos guste:
f(\lambda) = \det(A-\lambda I_3) = -\lambda^3 + 4\lambda^2 - 6\lambda + 4. \nonumber
Buscamos una raíz real utilizando el teorema de raíz racional. Las posibles raíces racionales son las que\pm 1,\pm 2,\pm 4\text{;} encontramosf(2) = 0\text{,} para que\lambda-2 se dividaf(\lambda). La realización de la división larga polinomial da
f(\lambda) = -(\lambda-2)\bigl(\lambda^2-2\lambda+2\bigr). \nonumber
El término cuadrático tiene raíces
\lambda = \frac{2\pm\sqrt{4-8}}2 = 1\pm i, \nonumber
para que la lista completa de valores propios sea\lambda_1 = 1-i\text{,}\bar\lambda_1 = 1+i\text{,} y\lambda_2 = 2.
Ahora calculamos algunos vectores propios, empezando por\lambda_1=1-i. Remaremos reducir (probablemente con la ayuda de una computadora):
A-(1-i)I_3 = \frac 1{29}\left(\begin{array}{ccc}4+29i&-23&9\\22&4+29i&-23\\19&14&21+29i\end{array}\right) \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{ccc}1&0&7/5+i/5 \\ 0&1&-2/5+9i/5 \\ 0&0&0\end{array}\right). \nonumber
La variable libre esz\text{,} y la forma paramétrica es
\left\{\begin{array}{ccc}x &=& -\left(\dfrac 75+\dfrac 15i\right)z\\ y &=& \left(\dfrac 25-\dfrac 95i\right)z\end{array}\right. \quad\xrightarrow[\text{eigenvector}]{z=5}\quad v_1=\left(\begin{array}{c}-7-i\\2-9i\\5\end{array}\right).\nonumber
Para\lambda_2=2\text{,} nosotros tenemos
A - 2I_3 = \frac 1{29}\left(\begin{array}{ccc}-25&-23&9\\22&-25&-23\\19&14&-8\end{array}\right) \;\xrightarrow{\text{RREF}}\; \left(\begin{array}{ccc}1&0&-2/3 \\ 0&1&1/3 \\ 0&0&0\end{array}\right). \nonumber
La variable libre esz\text{,} y la forma paramétrica es
\left\{\begin{array}{rrr}x &=& \dfrac 23z \\ y &=& -\dfrac 13z \end{array}\right. \quad\xrightarrow[\text{eigenvector}]{z=3}\quad v_2=\left(\begin{array}{c}2\\-1\\3\end{array}\right).\nonumber
Según el teorema\PageIndex{2}, tenemosA=CBC^{-1} para
\begin{aligned}C&=\left(\begin{array}{ccc}|&|&| \\ \Re(v_1)&\Im(v_1)&v_2 \\ |&|&|\end{array}\right)=\left(\begin{array}{ccc}-7&-1&2\\2&-9&-1\\5&0&3\end{array}\right) \\ B&=\left(\begin{array}{ccc}\Re(\lambda_1)&\Im(\lambda_1)&0 \\ -\Im(\lambda_1)&\Re(\lambda_1)&0 \\ 0&0&2\end{array}\right)=\left(\begin{array}{ccc}1&-1&0\\1&1&0\\0&0&2\end{array}\right).\end{aligned}
La matrizB es una combinación de la matriz de escala de rotación\left(\begin{array}{cc}1&-1\\1&1\end{array}\right) de Ejemplo\PageIndex{4}, y una matriz diagonal. Más específicamente,B actúa sobre lasxy coordenadas girando en sentido contrario a las agujas del reloj45^\circ y escalando por\sqrt2\text{,} y escala laz coordenada por2. Esto significa que los puntos por encima de la espiralxy -plano fuera delz eje -y se mueven hacia arriba, y los puntos por debajo de la espiralxy -plano fuera delz eje -y se mueven hacia abajo.
La matrizA hace lo mismo queB\text{,} pero con respecto al sistema\{\Re(v_1),\Im(v_1),v_2\} -coordenada. Es decir,A actúa sobre el\Re(v_1),\Im(v_1) plano al salir en espiral, yA actúa sobre lav_2 coordenada escalando por un factor de2. Vea la demo a continuación.