6.1: Productos punteados y ortogonalidad
- Page ID
- 113093
- Entender la relación entre el producto de punto, la longitud y la distancia.
- Entender la relación entre el producto punto y la ortogonalidad.
- Palabras de vocabulario: producto punto, longitud, distancia, vector unitario, vector unitario en la dirección de\(x\).
- Vocabulario esencial palabra: ortogonal.
En este capítulo, será necesario encontrar el punto más cercano en un subespacio a un punto dado, así:
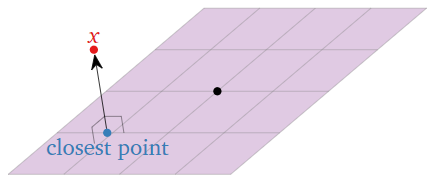
Figura\(\PageIndex{1}\)
El punto más cercano tiene la propiedad de que la diferencia entre los dos puntos es ortogonal, o perpendicular, al subespacio. Por esta razón, necesitamos desarrollar nociones de ortogonalidad, longitud y distancia.
El producto Dot
La construcción básica en esta sección es el producto punto, que mide ángulos entre vectores y computa la longitud de un vector.
El producto de punto de dos vectores\(x,y\) en\(\mathbb{R}^n \) es
\[ x\cdot y = \left(\begin{array}{c}x_1\\x_2\\ \vdots\\x_n\end{array}\right) \cdot \left(\begin{array}{c}y_1\\y_2\\ \vdots\\ y_n\end{array}\right) \;=\; x_1y_1 + x_2y_2 + \cdots + x_ny_n. \nonumber \]
Pensando en vectores de\(x,y\) columna, esto es lo mismo que\(x^Ty\).
Por ejemplo,
\[ \left(\begin{array}{c}1\\2\\3\end{array}\right)\cdot\left(\begin{array}{c}4\\5\\6\end{array}\right) = \left(\begin{array}{ccc}1&2&3\end{array}\right)\left(\begin{array}{c}4\\5\\6\end{array}\right) = 1\cdot 4 + 2\cdot 5 + 3\cdot 6 = 32. \nonumber \]
Observe que el producto punto de dos vectores es un escalar.
Puedes hacer aritmética con productos punteados mayormente como de costumbre, siempre y cuando recuerdes solo puedes puntear dos vectores juntos, y que el resultado sea un escalar.
Dejar\(x,y,z\) ser vectores adentro\(\mathbb{R}^n \) y dejar\(c\) ser un escalar.
- Conmutatividad:\(x\cdot y = y \cdot x\).
- Distributividad con adición:\((x + y)\cdot z = x\cdot z+y\cdot z\).
- Distributividad con multiplicación escalar:\((cx)\cdot y = c(x\cdot y)\).
El producto de punto de un vector consigo mismo es un caso especial importante:
\[ \left(\begin{array}{c}x_1\\x_2\\ \vdots\\x_n\end{array}\right) \cdot\left(\begin{array}{c}x_1\\x_2\\ \vdots\\x_n\end{array}\right) = x_1^2 + x_2^2 + \cdots + x_n^2. \nonumber \]
Por lo tanto, para cualquier vector\(x\text{,}\) tenemos:
- \(x\cdot x \geq 0\)
- \(x\cdot x = 0 \iff x = 0.\)
Esto lleva a una buena definición de longitud.
La longitud de un vector\(x\) en\(\mathbb{R}^n \) es el número
\[ \|x\| = \sqrt{x\cdot x} = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}. \nonumber \]
Es fácil ver por qué esto es cierto para los vectores en\(\mathbb{R}^2 \text{,}\) por el teorema de Pitágoras.
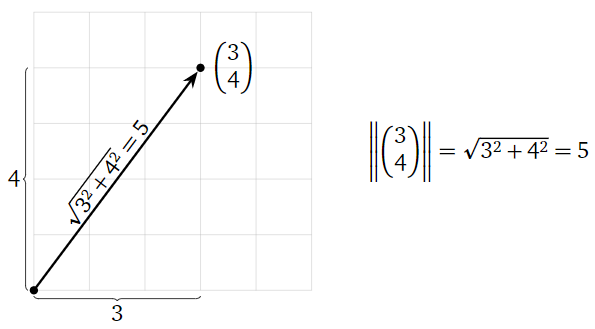
Figura\(\PageIndex{1}\)
Para vectores en\(\mathbb{R}^3 \text{,}\) uno se puede comprobar que\(\|x\|\) realmente es la longitud de\(x\text{,}\) aunque ahora esto requiere de dos aplicaciones del teorema de Pitágoras.
Tenga en cuenta que la longitud de un vector es la longitud de la flecha; si pensamos en términos de puntos, entonces la longitud es su distancia desde el origen.
Supongamos que\(\|x\| = 2,\;\|y\|=3,\) y\(x\cdot y = -4\). Qué es\(\|2x + 3y\|\text{?}\)
Solución
Nosotros computamos
\[ \begin{split} \|2x+3y\|^2 &= (2x+3y)\cdot(2x+3y) \\ &= 4x\cdot x + 6x\cdot y + 6x\cdot y + 9y\cdot y \\ &= 4\|x\|^2 + 9\|y\|^2 + 12x\cdot y \\ &= 4\cdot 4 + 9\cdot 9 - 12\cdot 4 = 49. \end{split} \nonumber \]
De ahí\(\|2x+3y\| = \sqrt{49} = 7.\)
Si\(x\) es un vector y\(c\) es un escalar, entonces\(\|cx\|=|c|\cdot\|x\|.\)
Esto dice que escalar un vector por\(c\) escala su longitud por\(|c|\). Por ejemplo,
\[ \left\|\left(\begin{array}{c}6\\8\end{array}\right)\right\| = \left\|2\left(\begin{array}{c}3\\4\end{array}\right)\right\| = 2\left\|\left(\begin{array}{c}3\\4\end{array}\right)\right\| = 10. \nonumber \]
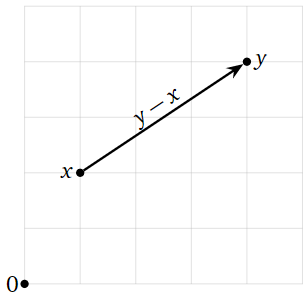
Ahora que tenemos una buena noción de longitud, podemos definir la distancia entre puntos en\(\mathbb{R}^n \). Recordemos que la diferencia entre dos puntos\(x,y\) es naturalmente un vector, es decir, el vector\(y-x\) que apunta de\(x\) a\(y\).
La distancia entre dos puntos\(x,y\) en\(\mathbb{R}^n \) es la longitud del vector desde, Nota 2.1.2 en la Sección 2.1,\(x\) a\(y\text{:}\)
\[ \text{dist}(x,y) = \|y-x\|. \nonumber \]
Encuentra la distancia de\((1,2)\) a\((4,4)\).
Solución
Dejar\(x=(1,2)\) y\(y=(4,4)\). Entonces
\[ \text{dist}(x,y) = \|y-x\| = \left\|\left(\begin{array}{c}3\\2\end{array}\right)\right\| = \sqrt{3^2+2^2} = \sqrt{13}. \nonumber \]
Figura\(\PageIndex{2}\)
Los vectores con longitud\(1\) son muy comunes en las aplicaciones, por lo que les damos un nombre.
Un vector unitario es un vector\(x\) con longitud\(\|x\| = \sqrt{x\cdot x} =1\).
Los vectores de coordenadas estándar, Nota 3.3.2 en la Sección 3.3,\(e_1,e_2,e_3,\ldots\) son vectores unitarios:
\[ \|e_1\| = \left\|\left(\begin{array}{c}1\\0\\0\end{array}\right)\right\| = \sqrt{1^2 + 0^2 + 0^2} = 1. \nonumber \]
Para cualquier vector distinto de cero\(x\text{,}\) hay un vector unitario único que apunta en la misma dirección. Se obtiene dividiendo por la longitud de\(x\).
Dejar\(x\) ser un vector distinto de cero en\(\mathbb{R}^n \). El vector unitario en la dirección de\(x\) es el vector\(x/\|x\|\).
Esto es de hecho un vector unitario (señalando que\(\|x\|\) es un número positivo, entonces\(\bigl|1/\|x\|\bigr| = 1/\|x\|\)):
\[ \left\|\frac{x}{\|x\|}\right\| = \frac 1{\|x\|}\|x\| = 1. \nonumber \]
¿Cuál es el vector unitario\(u\) en la dirección de\(x = \left(\begin{array}{c}3\\4\end{array}\right)\text{?}\)
Solución
Dividimos por la longitud de\(x\text{:}\)
\[ u = \frac{x}{\|x\|} = \frac 1{\sqrt{3^2+4^2}}\left(\begin{array}{c}3\\4\end{array}\right) = \frac{1}{5}\left(\begin{array}{c}3\\4\end{array}\right) = \left(\begin{array}{c}3/5\\4/5\end{array}\right). \nonumber \]
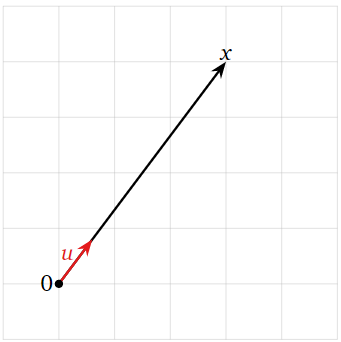
Figura\(\PageIndex{3}\)
Vectores ortogonales
En esta sección, mostramos cómo se puede utilizar el producto punto para definir la ortogonalidad, es decir, cuando dos vectores son perpendiculares entre sí.
Dos vectores\(x,y\) en\(\mathbb{R}^n \) son ortogonales o perpendiculares si\(x\cdot y = 0\).
Notación:\(x\perp y\) medias\(x\cdot y = 0\).
Dado que\(0 \cdot x = 0\) para cualquier vector\(x\text{,}\) el vector cero es ortogonal a cada vector en\(\mathbb{R}^n \).
Motivamos la definición anterior utilizando la ley de los cosenos en\(\mathbb{R}^2 \). En nuestro lenguaje, la ley de los cosenos afirma que si\(x,y\) son dos vectores distintos de cero, y si\(\alpha>0\) es el ángulo entre ellos, entonces
\[ \|y-x\|^2 = \|x\|^2 + \|y\|^2 - 2\|x\|\,\|y\|\cos\alpha. \nonumber \]
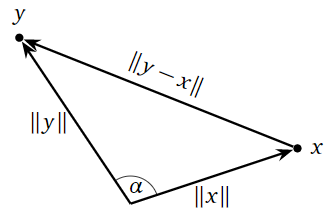
Figura\(\PageIndex{4}\)
En particular,\(\alpha=90^\circ\) si y sólo si\(\cos(\alpha)=0\text{,}\) que sucede si y sólo si\(\|y-x\|^2 = \|x\|^2+\|y\|^2\). Por lo tanto,
\[ \begin{split} \text{$x$ and $y$ are perpendicular} \amp\iff \|x\|^2 + \|y\|^2 = \|y-x\|^2 \\ \amp\iff x\cdot x + y\cdot y = (y-x)\cdot(y-x) \\ \amp\iff x\cdot x + y\cdot y = y\cdot y + x\cdot x -2x\cdot y \\ \amp\iff x\cdot y = 0. \end{split} \nonumber \]
Reiterar:
\[ x\perp y \quad\iff\quad x\cdot y = 0 \quad\iff\quad \|y-x\|^2 = \|x\|^2 + \|y\|^2. \nonumber \]
Encuentra todos los vectores ortogonal a\(v = \left(\begin{array}{c}1\\1\\-1\end{array}\right).\)
Solución
Tenemos que encontrar todos los vectores\(x\) tal que\(x\cdot v = 0\). Esto significa resolver la ecuación
\[ 0 = x\cdot v = \left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\-1\end{array}\right) = x_1 + x_2 - x_3. \nonumber \]
La forma paramétrica para el conjunto de soluciones es\(x_1 = -x_2 + x_3\text{,}\) así que la forma vectorial paramétrica de la solución general es
\[ x = \left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right) = x_2\left(\begin{array}{c}-1\\1\\0\end{array}\right) + x_3\left(\begin{array}{c}1\\0\\1\end{array}\right). \nonumber \]
Por lo tanto, la respuesta es el plano
\[ \text{Span}\left\{\left(\begin{array}{c}-1\\1\\0\end{array}\right),\;\left(\begin{array}{c}1\\0\\1\end{array}\right)\right\}. \nonumber \]
Por ejemplo,
\[\left(\begin{array}{c}-1\\1\\0\end{array}\right)\perp\left(\begin{array}{c}1\\1\\-1\end{array}\right)\quad\text{because}\quad \left(\begin{array}{c}-1\\1\\0\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\-1\end{array}\right) = 0\text{.} \nonumber \]
Encuentra todos los vectores ortogonales a ambos\(v = \left(\begin{array}{c}1\\1\\-1\end{array}\right)\) y\(w = \left(\begin{array}{c}1\\1\\1\end{array}\right)\).
Solución
Tenemos que resolver el sistema de dos ecuaciones homogéneas
\[\begin{aligned}0&=x\cdot v=\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\-1\end{array}\right)=x_1+x_2-x_3 \\ 0&=x\cdot w=\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\1\end{array}\right)=x_1+x_2+x_3.\end{aligned}\]
En forma de matriz:
\[ \left(\begin{array}{ccc}1&1&-1\\1&1&1\end{array}\right) \;\xrightarrow{\text{RREF}}\;\left(\begin{array}{ccc}1&1&0\\0&0&1\end{array}\right). \nonumber \]
La forma vectorial paramétrica del conjunto de soluciones es
\[ \left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right) = x_2\left(\begin{array}{c}-1\\1\\0\end{array}\right). \nonumber \]
Por lo tanto, la respuesta es la línea
\[ \text{Span}\left\{\left(\begin{array}{c}-1\\1\\0\end{array}\right)\right\}. \nonumber \]
Por ejemplo,
\[ \left(\begin{array}{c}-1\\1\\0\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\-1\end{array}\right) = 0 \quad\text{and}\quad \left(\begin{array}{c}-1\\1\\0\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\1\end{array}\right) = 0. \nonumber \]
De manera más general, la ley de los cosenos da una fórmula para el ángulo\(\alpha\) entre dos vectores distintos de cero:
\[ \begin{split} 2\|x\|\|y\|\cos(\alpha) \amp= \|x\|^2 + \|y\|^2 - \|y-x\|^2 \\ \amp= x\cdot x + y\cdot y - (y-x)\cdot (y-x) \\ \amp= x\cdot x + y\cdot y - y\cdot y - x\cdot x + 2x\cdot y \\ \amp= 2x\cdot y \\ \amp\quad\implies \alpha = \cos^{-1}\left(\frac{x\cdot y}{\|x\|\|y\|}\right). \end{split} \nonumber \]
En dimensiones superiores, tomamos esta como la definición del ángulo entre\(x\) y\(y\).


