5: Sistema de ecuaciones

Última actualización
Guardar como PDF

Page ID: 119376

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Después de leer este capítulo, deberías poder:

configurar ecuaciones lineales simultáneas en forma de matriz y viceversa,
entender el concepto de la inversa de una matriz,
conocer la diferencia entre un sistema consistente e inconsistente de ecuaciones lineales, y
aprender que un sistema de ecuaciones lineales puede tener una solución única, ninguna solución o infinitas soluciones.

El álgebra matricial se utiliza para resolver sistemas de ecuaciones. ¿Puedes ilustrar este concepto?

El álgebra matricial se utiliza para resolver un sistema de ecuaciones lineales simultáneas. De hecho, para muchos procedimientos matemáticos como la solución a un conjunto de ecuaciones no lineales, interpolación, integración y ecuaciones diferenciales, las soluciones se reducen a un conjunto de ecuaciones lineales simultáneas. Ilustremos con un ejemplo para la interpolación.

Ejemplo 1

La velocidad ascendente de un cohete se da en tres momentos diferentes en la siguiente tabla.

Cuadro 5.1. Datos de velocidad vs. tiempo para un cohete
Tiempo, t	Velocidad, v
(s)	(m/s)
5	106.8
8	177.2
12	279.2

Los datos de velocidad son aproximados por un polinomio como

\[v\left( t \right) = at^{2} + {bt} + c,5 \leq t \leq 12 \nonumber \]

Configure las ecuaciones en forma de matriz para encontrar los coeficientes$a,b,c$ del perfil de velocidad.

Solución

El polinomio está pasando por tres puntos de datos$\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),and\left( t_{3},v_{3} \right)$ donde de la tabla 5.1.

\[t_{1} = 5,\ v_{1} = 106.8 \nonumber \]

\[t_{2} = 8,\ v_{2} = 177.2 \nonumber \]

\[t_{3} = 12,\ v_{3} = 279.2 \nonumber \]

Requerir que$v\left( t \right) = at^{2} + {bt} + c$ pasa por los tres puntos de datos da

\[v\left( t_{1} \right) = v_{1} = at_{1}^{2} + bt_{1} + c \nonumber \]

\[v\left( t_{2} \right) = v_{2} = at_{2}^{2} + bt_{2} + c \nonumber \]

\[v\left( t_{3} \right) = v_{3} = at_{3}^{2} + bt_{3} + c \nonumber \]

Sustituir los datos$\left( t_{1},v_{1} \right),\left( t_{2},v_{2} \right),\ and\ \left( t_{3},v_{3} \right)$ da

\[a\left( 5^{2} \right) + b\left( 5 \right) + c = 106.8 \nonumber \]

\[a\left( 8^{2} \right) + b\left( 8 \right) + c = 177.2 \nonumber \]

\[a\left( 12^{2} \right) + b\left( 12 \right) + c = 279.2 \nonumber \]

\[25a + 5b + c = 106.8 \nonumber \]

\[64a + 8b + c = 177.2 \nonumber \]

\[144a + 12b + c = 279.2 \nonumber \]

Este conjunto de ecuaciones se puede reescribir en forma de matriz como

\[\begin{bmatrix} 25a + & 5b + & c \\ 64a + & 8b + & c \\ 144a + & 12b + & c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

La ecuación anterior se puede escribir como una combinación lineal de la siguiente manera

\[a\begin{bmatrix} 25 \\ 64 \\ 144 \\ \end{bmatrix} + b\begin{bmatrix} 5 \\ 8 \\ 12 \\ \end{bmatrix} + c\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

y además el uso de la multiplicación matricial da

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

Lo anterior es una ilustración de por qué se necesita álgebra matricial. La solución completa al conjunto de ecuaciones se da más adelante en este capítulo.

Un conjunto general de ecuaciones$m$ lineales e$n$ incógnitas,

\[a_{11}x_{1} + a_{12}x_{2} + \cdots\cdots + a_{1n}x_{n} = c_{1} \nonumber \]

\[a_{21}x_{1} + a_{22}x_{2} + \cdots\cdots + a_{2n}x_{n} = c_{2} \nonumber \]

\[ \text{..........................................} \nonumber \]

\[a_{m1}x_{1} + a_{m2}x_{2} + ........ + a_{mn}x_{n} = c_{m} \nonumber \]

se puede reescribir en forma de matriz como

\[\begin{bmatrix} a_{11} & a_{12} & . & . & a_{1n} \\ a_{21} & a_{22} & . & . & a_{2n} \\ \vdots & & & & \vdots \\ \vdots & & & & \vdots \\ a_{m1} & a_{m2} & . & . & a_{mn} \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ \cdot \\ \cdot \\ x_{n} \\ \end{bmatrix} = \begin{bmatrix} c_{1} \\ c_{2} \\ \cdot \\ \cdot \\ c_{m} \\ \end{bmatrix} \nonumber \]

Denotando las matrices por$\left\lbrack A \right\rbrack$$\left\lbrack X \right\rbrack$, y$\left\lbrack C \right\rbrack$, el sistema de ecuación es

$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$, donde$\left\lbrack A \right\rbrack$ se llama la matriz de coeficientes,$\left\lbrack C \right\rbrack$ se llama el vector del lado derecho y$\left\lbrack X \right\rbrack$ se llama el vector de solución.

A veces$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ los sistemas de ecuaciones se escriben en forma aumentada. Eso es

\[\left\lbrack A \ \vdots \ C \right\rbrack = \left\lbrack \begin{matrix} a_{11} & a_{12} & {......} & a_{1n} \\ a_{21} & a_{22} & {......} & a_{2n} \\ \begin{matrix} \vdots \\ \vdots \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} & \begin{matrix} \\ \\ \end{matrix} \\ a_{m1} & a_{m2} & {......} & a_{mn} \\ \end{matrix}\begin{matrix} \vdots \\ \vdots \\ \vdots \\ \vdots \\ \vdots \\ \end{matrix}\begin{matrix} c_{1} \\ c_{2} \\ \\ \\ c_{n} \\ \end{matrix} \right\rbrack \nonumber \]

Un sistema de ecuaciones puede ser consistente o inconsistente. ¿Qué significa eso?

Un sistema de ecuaciones$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ es consistente si hay una solución, y es inconsistente si no hay solución. Sin embargo, un sistema consistente de ecuaciones no significa una solución única, es decir, un sistema consistente de ecuaciones puede tener una solución única o soluciones infinitas (Figura 1).

Figura$\PageIndex{1}$: Diagrama de flujo del sistema consistente e inconsistente de ecuaciones.

Ejemplo 2

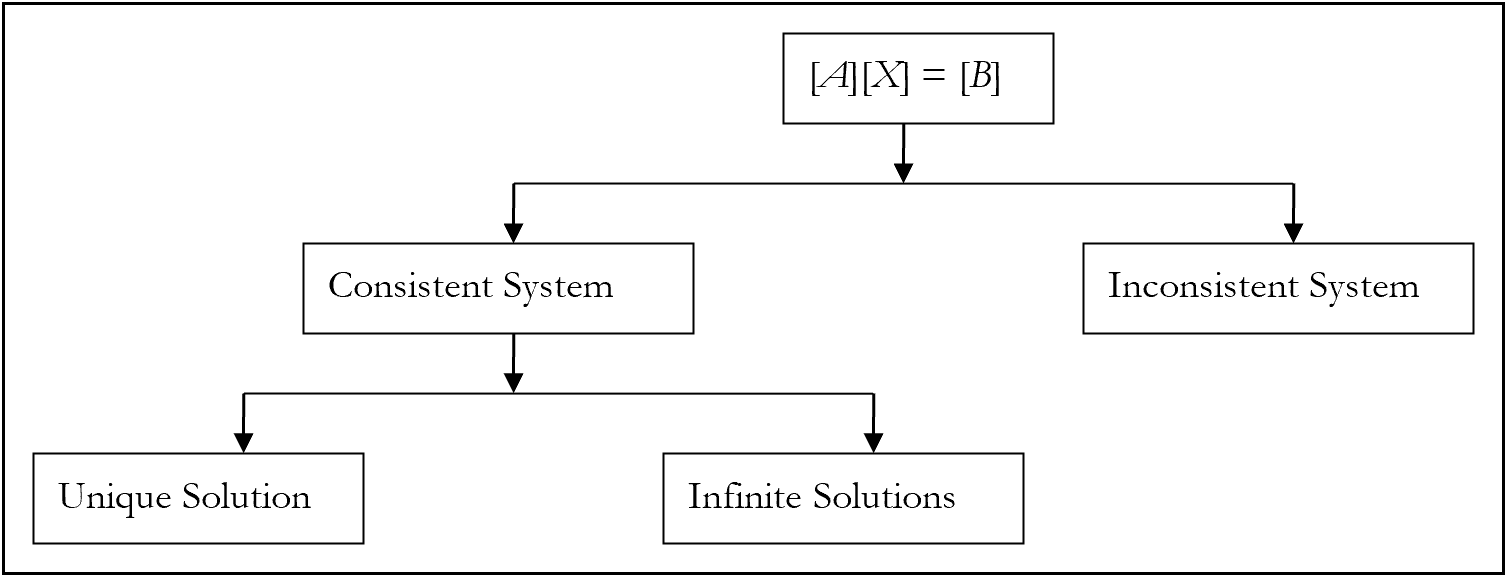
Dar ejemplos de sistema consistente e inconsistente de ecuaciones.

Solución

El sistema de ecuaciones

\[\begin{bmatrix} 2 & 4 \\ 1 & 3 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ \end{bmatrix} \nonumber \]

es un sistema consistente de ecuaciones ya que tiene una solución única, es decir,

\[\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ \end{bmatrix} \nonumber \]

El sistema de ecuaciones

\[\begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 3 \\ \end{bmatrix} \nonumber \]

es también un sistema consistente de ecuaciones pero tiene infinitas soluciones como se da de la siguiente manera.

Ampliando el conjunto de ecuaciones anterior,

\[2x + 4y = 6 \nonumber \]

\[x + 2y = 3 \nonumber \]

se puede ver que son la misma ecuación. Por lo tanto, cualquier combinación de$\left( x,y \right)$ eso satisface

\[2x + 4y = 6 \nonumber \]

es una solución. Por ejemplo$\left( x,y \right) = \left( 1,1 \right)$ es una solución. Otras soluciones incluyen$\left( x,y \right) = (0.5,1.25)$,$\left( x,y \right) = (0,1.5)$, y así sucesivamente.

El sistema de ecuaciones

\[\begin{bmatrix} 2 & 4 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 4 \\ \end{bmatrix} \nonumber \]

es inconsistente ya que no existe ninguna solución.

¿Cómo se puede distinguir entre un sistema consistente e inconsistente de ecuaciones?

Un sistema de ecuaciones$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ es consistente si el rango de$A$ es igual al rango de la matriz aumentada$\left\lbrack A \ \vdots \ C \right\rbrack$

Un sistema de ecuaciones$\left\lbrack A \right\rbrack\ \left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ es inconsistente si el rango de$A$ es menor que el rango de la matriz aumentada$\left\lbrack A \ \vdots \ C \right\rbrack$.

Pero, ¿qué quiere decir con rango de una matriz?

El rango de una matriz se define como el orden de la submatriz cuadrada más grande cuyo determinante no es cero.

Ejemplo 3

¿Cuál es el rango de

$\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 1 & 2 \\ 2 & 0 & 5 \\ 1 & 2 & 3 \\ \end{bmatrix}$?

Solución

La submatriz cuadrada más grande posible es del orden 3 y esa es$\lbrack A\rbrack$ en sí misma. Desde$det(A) = - 23 \neq 0,$ el rango de$\lbrack A\rbrack = 3.$

Ejemplo 4

¿Cuál es el rango de

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 1 & 2 \\ 2 & 0 & 5 \\ 5 & 1 & 7 \\ \end{bmatrix}? \nonumber \]

Solución

La submatriz cuadrada más grande de$\lbrack A\rbrack$ es del orden 3 y esa es$\lbrack A\rbrack$ en sí misma. Ya que$det(A) = 0$, el rango de$\lbrack A\rbrack$ es menor a 3. La siguiente submatriz cuadrada más grande sería una$2 \times2$ matriz. Una de las submatrices cuadradas de$\lbrack A\rbrack$ es

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 3 & 1 \\ 2 & 0 \\ \end{bmatrix} \nonumber \]

y$det(B) = - 2 \neq 0$. De ahí que el rango de$\lbrack A\rbrack$ sea 2. No hay necesidad de mirar otras$2 \times 2$ submatrices para establecer que el rango de$\lbrack A\rbrack$ es 2.

Ejemplo 5

¿Cómo utilizo ahora el concepto de rango para encontrar si

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

es un sistema consistente o inconsistente de ecuaciones?

Solución

La matriz de coeficientes es

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

y el vector del lado derecho es

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

La matriz aumentada es

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & \vdots & 106.8 \\ 64 & 8 & 1 & \vdots & 177.2 \\ 144 & 12 & 1 & \vdots & 279.2 \\ \end{bmatrix} \nonumber \]

Dado que no hay submatrices cuadradas de orden 4 como$\lbrack B\rbrack$ es una$3 \times 3$ matriz, el rango de$\lbrack B\rbrack$ es como máximo$3$. Entonces veamos las submatrices cuadradas$\lbrack B\rbrack$ de orden$3$; si alguna de estas submatrices cuadradas tiene determinante no igual a cero, entonces el rango es$3$. Por ejemplo, una submatriz de la matriz aumentada$\lbrack B\rbrack$ es

\[\lbrack D\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

tiene$det(D) = - 84 \neq 0$.

De ahí que el rango de la matriz aumentada$\lbrack B\rbrack$ sea 3. Ya que$\lbrack A\rbrack = \lbrack D\rbrack$, el rango de$\lbrack A\rbrack$ es 3. Dado que el rango de la matriz aumentada$\lbrack B\rbrack$ es igual al rango de la matriz de coeficientes$\lbrack A\rbrack$, el sistema de ecuaciones es consistente.

Ejemplo 6

Usa el concepto de rango de matriz para encontrar si

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 284.0 \\ \end{bmatrix} \nonumber \]

¿es consistente o inconsistente?

Solución

La matriz de coeficientes viene dada por

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

y el lado derecho

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 284.0 \\ \end{bmatrix} \nonumber \]

La matriz aumentada es

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & :106.8 \\ 64 & 8 & 1 & :177.2 \\ 89 & 13 & 2 & :284.0 \\ \end{bmatrix} \nonumber \]

Dado que no hay submatrices cuadradas de orden 4 como$\lbrack B\rbrack$ es una$4 \times 3$ matriz, el rango de los aumentados$\lbrack B\rbrack$ es como máximo 3. Entonces veamos las submatrices cuadradas de la matriz aumentada$\lbrack B\rbrack$ de orden$3$ y veamos si alguna de estas tiene determinantes no iguales a cero. Por ejemplo, una submatriz cuadrada de la matriz aumentada$\lbrack B\rbrack$ es

\[\left\lbrack D \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

tiene$det(D) = 0$. Esto significa que necesitamos explorar otras submatrices cuadradas de orden 3 de la matriz aumentada$\lbrack B\rbrack$ y encontrar sus determinantes.

Es decir,

\[\left\lbrack E \right\rbrack = \begin{bmatrix} 5 & 1 & 106.8 \\ 8 & 1 & 177.2 \\ 13 & 2 & 284.0 \\ \end{bmatrix} \nonumber \]

\[det(E) = 0 \nonumber \]

\[\left\lbrack F \right\rbrack = \begin{bmatrix} 25 & 5 & 106.8 \\ 64 & 8 & 177.2 \\ 89 & 13 & 284.0 \\ \end{bmatrix} \nonumber \]

\[det(F) = 0 \nonumber \]

\[\left\lbrack G \right\rbrack = \begin{bmatrix} 25 & 1 & 106.8 \\ 64 & 1 & 177.2 \\ 89 & 2 & 284.0 \\ \end{bmatrix} \nonumber \]

\[det(G) = 0 \nonumber \]

Todas las submatrices cuadradas de orden$3 \times 3$ de la matriz aumentada$\lbrack B\rbrack$ tienen un determinante cero. Entonces el rango de la matriz aumentada$\lbrack B\rbrack$ es menor a 3. ¿El rango de matriz aumentada es$\lbrack B\rbrack$ igual a 2?. Una de las$2 \times 2$ submatrices de la matriz aumentada$\lbrack B\rbrack$ es

\[\left\lbrack H \right\rbrack = \begin{bmatrix} 25 & 5 \\ 64 & 8 \\ \end{bmatrix} \nonumber \]

\[det(H) = - 120 \neq 0 \nonumber \]

Entonces, el rango de la matriz aumentada$\lbrack B\rbrack$ es 2.

Ahora necesitamos encontrar el rango de la matriz de coeficientes$\lbrack B\rbrack$.

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

\[det(A) = 0 \nonumber \]

Entonces, el rango de la matriz de coeficientes$\lbrack A\rbrack$ es menor a 3. Una submatriz cuadrada de la matriz de coeficientes$\lbrack A\rbrack$ es

\[\left\lbrack J \right\rbrack = \begin{bmatrix} 5 & 1 \\ 8 & 1 \\ \end{bmatrix} \nonumber \]

\[det(J) = - 3 \neq 0 \nonumber \]

Entonces, el rango de la matriz de coeficientes$\lbrack A\rbrack$ es 2.

De ahí que el rango de la matriz de coeficientes$\lbrack A\rbrack$ sea igual al rango de la matriz aumentada$[B]$. Entonces el sistema de ecuaciones$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ es consistente.

Ejemplo 7

Usa el concepto de rango para encontrar si

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 280.0 \\ \end{bmatrix} \nonumber \]

es consistente o inconsistente.

Solución

La matriz aumentada es

\[\left\lbrack B \right\rbrack = \begin{bmatrix} 25 & 5 & 1 & :106.8 \\ 64 & 8 & 1 & :177.2 \\ 89 & 13 & 2 & :280.0 \\ \end{bmatrix} \nonumber \]

Dado que no hay submatrices cuadradas de orden$4 \times 4$ ya que la matriz aumentada$\lbrack B\rbrack$ es una$4 \times 3$ matriz, el rango de la matriz aumentada$\lbrack B\rbrack$ es como máximo 3. Entonces veamos las submatrices cuadradas de la matriz aumentada$(B)$ de orden 3 y veamos si alguna de las$3 \times 3$ submatrices tiene un determinante no igual a cero. Por ejemplo, una submatriz cuadrada del orden$3 \times 3$ de$\lbrack B\rbrack$

\[\left\lbrack D \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix} \nonumber \]

\[\det(D)\ = \ 0 \nonumber \]

Entonces, significa, necesitamos explorar otras submatrices cuadradas de la matriz aumentada$\lbrack B\rbrack$

\[\left\lbrack E \right\rbrack = \begin{bmatrix} 5 & 1 & 106.8 \\ 8 & 1 & 177.2 \\ 13 & 2 & 280.0 \\ \end{bmatrix} \nonumber \]

$det(E) = 12.0 \neq 0$.

Entonces, el rango de la matriz aumentada$\lbrack B\rbrack$ es 3.

El rango de la matriz de coeficientes$\lbrack A\rbrack$ es 2 del ejemplo anterior.

Dado que el rango de la matriz de coeficientes$\lbrack A\rbrack$ es menor que el rango de la matriz aumentada$\lbrack B\rbrack$, el sistema de ecuaciones es inconsistente. De ahí que no exista solución para$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$.

Si existe una solución, ¿cómo sabemos si es única?

En un sistema de ecuaciones$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ que es consistente, el rango de la matriz de coeficientes$\lbrack A\rbrack$ es el mismo que el de la matriz aumentada$\lbrack A\left| C \right.\ \rbrack$. Si además, el rango de la matriz de coeficientes$\lbrack A\rbrack$ es el mismo que el número de incógnitas, entonces la solución es única; si el rango de la matriz de coeficientes$\lbrack A\rbrack$ es menor que el número de incógnitas, entonces existen infinitas soluciones.

Figura$\PageIndex{2}$: Diagrama de flujo de condiciones para un sistema consistente e inconsistente de ecuaciones.

Ejemplo 8

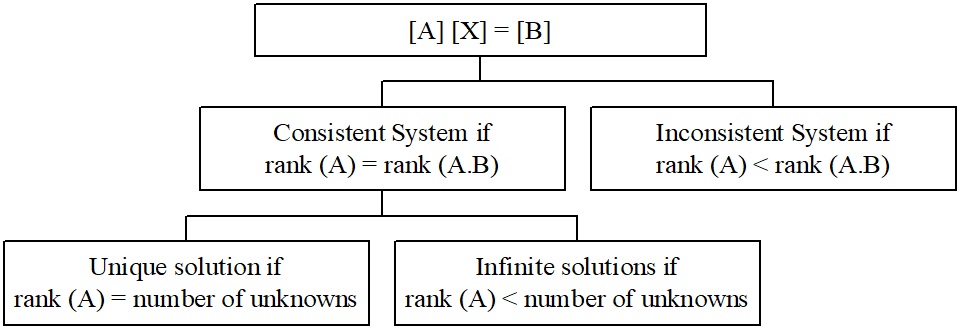
Encontramos que el siguiente sistema de ecuaciones

es un sistema consistente de ecuaciones. ¿El sistema de ecuaciones tiene una solución única o tiene infinitas soluciones?

Solución

La matriz de coeficientes es

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

y el lado derecho es

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

Si bien averiguamos si las ecuaciones anteriores eran consistentes en un ejemplo anterior, encontramos que el rango de la matriz de coeficientes (A) es igual al rango de la matriz aumentada$\left\lbrack A \ \vdots \ C \right\rbrack$ es igual a 3.

La solución es única ya que el número de incógnitas = 3 = rango de (A).

Ejemplo 9

Encontramos que el siguiente sistema de ecuaciones

es un sistema consistente de ecuaciones. Es la solución única o tiene infinitas soluciones.

Solución

Al tiempo que averiguamos si las ecuaciones anteriores eran consistentes, encontramos que el rango de la matriz de coeficientes$\lbrack A\rbrack$ es igual al rango de matriz aumentada$\left( A \ \vdots\ C \right)$ es igual a 2

Dado que el rango de$\lbrack A\rbrack = 2$ < número de incógnitas = 3, existen infinitas soluciones.

Si tenemos más ecuaciones que incógnitas en [A] [X] = [C], ¿significa que el sistema es inconsistente?

No, depende del rango de la matriz aumentada$\left\lbrack A\ \vdots \ C \right\rbrack$ y del rango de$\lbrack A\rbrack$.

Por ejemplo

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ 284.0 \\ \end{bmatrix} \nonumber \]

es consistente, ya que

rango de matriz aumentada = 3
rango de matriz de coeficientes = 3

Ahora como el rango de (A) = 3 = número de incógnitas, la solución no sólo es consistente sino también única.

Por ejemplo

es inconsistente, ya que

rango de matriz aumentada =$4$
rango de matriz de coeficientes =$3$

Por ejemplo

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 50 & 10 & 2 \\ 89 & 13 & 2 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 213.6 \\ 280.0 \\ \end{bmatrix} \nonumber \]

es consistente, ya que

rango de matriz aumentada = 2
rango de matriz de coeficientes = 2

Pero como el rango de$\lbrack A\rbrack$ = 2 < el número de incógnitas = 3, existen infinitas soluciones.

Los sistemas consistentes de ecuaciones solo pueden tener una solución única o soluciones infinitas. ¿Puede un sistema de ecuaciones tener más de una pero no un número infinito de soluciones?

No, solo puedes tener una solución única o soluciones infinitas. Supongamos que$\lbrack A\rbrack\lbrack X\rbrack = \lbrack C\rbrack$ tiene dos soluciones$\lbrack Y\rbrack$ y$\lbrack Z\rbrack$ para que

\[\lbrack A\rbrack\lbrack Y\rbrack = \lbrack C\rbrack \nonumber \]

\[\lbrack A\rbrack\lbrack Z\rbrack = \lbrack C\rbrack \nonumber \]

Si$r$ es una constante, entonces de las dos ecuaciones

\[r\left\lbrack A \right\rbrack\left\lbrack Y \right\rbrack = r\left\lbrack C \right\rbrack \nonumber \]

\[\left( 1 - r \right)\left\lbrack A \right\rbrack\left\lbrack Z \right\rbrack = \left( 1 - r \right)\left\lbrack C \right\rbrack \nonumber \]

Sumando las dos ecuaciones anteriores da

\[r\left\lbrack A \right\rbrack\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack A \right\rbrack\left\lbrack Z \right\rbrack = r\left\lbrack C \right\rbrack + \left( 1 - r \right)\left\lbrack C \right\rbrack \nonumber \]

\[\left\lbrack A \right\rbrack\left( r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \right) = \left\lbrack C \right\rbrack \nonumber \]

De ahí

\[r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \nonumber \]

es una solución para

\[\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack \nonumber \]

Como$r$ es cualquier escalar, hay infinitas soluciones para$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ de la forma

\[r\left\lbrack Y \right\rbrack + \left( 1 - r \right)\left\lbrack Z \right\rbrack \nonumber \]

¿Se pueden dividir dos matrices?

Si$\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack C\rbrack$ se define, puede parecer intuitivo eso$\lbrack A\rbrack = \frac{\left\lbrack C \right\rbrack}{\left\lbrack B \right\rbrack}$, pero la división matricial no se define así. Sin embargo, se puede definir una inversa de una matriz para ciertos tipos de matrices cuadradas. El inverso de una matriz cuadrada$\lbrack A\rbrack$, si existe, se denota por$\lbrack A\rbrack^{- 1}$ tal que

\[\lbrack A\rbrack\ \lbrack A\rbrack^{- 1} = \lbrack I\rbrack = \lbrack A\rbrack^{- 1}\lbrack A\rbrack \nonumber \]

Dónde$\lbrack I\rbrack$ está la matriz de identidad.

En otras palabras, deja$[A]$ ser una matriz cuadrada. Si$\lbrack B\rbrack$ es otra matriz cuadrada del mismo tamaño tal que$\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack$, entonces$\lbrack B\rbrack$ es la inversa de$\lbrack A\rbrack$. $\lbrack A\rbrack$se llama entonces a ser invertible o no singular. Si$\lbrack A\rbrack^{- 1}$ no existe,$\lbrack A\rbrack$ se llama no invertible o singular.

Si$\lbrack A\rbrack$ y$\lbrack B\rbrack$ son dos$n \times n$ matrices tales que$\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack$, entonces estas afirmaciones también son verdaderas

$[B]$es la inversa de$[A]$

$[A]$es la inversa de$[B]$

$[A]$y ambos$[B]$ son invertibles

$[A]$$[B]$=$[I]$.

$[A]$y$[B]$ ambos no singulares

todas las columnas de$[A]$ y$[B]$ son linealmente independientes

todas las filas de$[A]$ y$[B]$ son linealmente independientes.

Ejemplo 10

Determinar si

\[\lbrack B\rbrack = \begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\ \nonumber \]

es la inversa de

\[\lbrack A\rbrack = \begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix} \nonumber \]

Solución

\[\begin{split} \lbrack B\rbrack\lbrack A\rbrack &= \ \ \begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\\ &= \lbrack I\rbrack \end{split} \nonumber \]

Desde

\[\ \left\lbrack B \right\rbrack\left\lbrack A \right\rbrack = \left\lbrack I \right\rbrack, \nonumber \]

$\lbrack B\rbrack$es la inversa de$[A]$ y$\lbrack A\rbrack$ es la inversa de$\lbrack B\rbrack$.

Pero, también podemos demostrar que

\[\begin{split} \lbrack A\rbrack\lbrack B\rbrack &= \begin{bmatrix} - 3 & 2 \\ 5 & - 3 \\ \end{bmatrix}\begin{bmatrix} 3 & 2 \\ 5 & 3 \\ \end{bmatrix}\\ &= \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\\ &= \lbrack I\rbrack \end{split} \nonumber \]

para mostrar que$\lbrack A\rbrack$ es la inversa de$\lbrack B\rbrack$.

¿Puedo usar el concepto de la inversa de una matriz para encontrar la solución de un conjunto de ecuaciones [A] [X] = [C]?

Sí, si el número de ecuaciones es el mismo que el número de incógnitas, la matriz de coeficientes$\lbrack A\rbrack$ es una matriz cuadrada.

Dado

\[\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack \nonumber \]

Entonces, si$\lbrack A\rbrack^{- 1}$ existe, multiplicando ambos lados por$\lbrack A\rbrack^{- 1}$.

\[\lbrack A\rbrack^{- 1}\lbrack A\rbrack\lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber \]

\[\lbrack I\rbrack\ \lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber \]

\[\lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack C\rbrack \nonumber \]

Esto implica que si somos capaces de encontrar$\lbrack A\rbrack^{- 1}$, el vector de solución de$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ es simplemente una multiplicación de$\lbrack A\rbrack^{- 1}$ y el vector del lado derecho,$\lbrack C\rbrack$.

¿Cómo encuentro la inversa de una matriz?

Si$\lbrack A\rbrack$ es una$n \times n$ matriz, entonces$\lbrack A\rbrack^{- 1}$ es una$n \times n$ matriz y de acuerdo con la definición de inversa de una matriz

\[\lbrack A\rbrack\ \lbrack A\rbrack^{- 1} = \lbrack I\rbrack \nonumber \]

Denotando

\[\lbrack A\rbrack = \begin{bmatrix} a_{11} & a_{12} & \cdot & \cdot & a_{1n} \\ a_{21} & a_{22} & \cdot & \cdot & a_{2n} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1} & a_{n2} & \cdot & \cdot & a_{nn} \\ \end{bmatrix} \nonumber \]

\[\lbrack A\rbrack^{- 1} = \begin{bmatrix} a_{11}^{'} & a_{12}^{'} & \cdot & \cdot & a_{1n}^{'} \\ a_{21}^{'} & a_{22}^{'} & \cdot & \cdot & a_{2n}^{'} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1}^{'} & a_{n2}^{'} & \cdot & \cdot & a_{nn}^{'} \\ \end{bmatrix} \nonumber \]

\[\lbrack I\rbrack = \begin{bmatrix} 1 & 0 & \cdot & \cdot & \cdot & 0 \\ 0 & 1 & & & & 0 \\ 0 & & \cdot & & & \cdot \\ \cdot & & & 1 & & \cdot \\ \cdot & & & & \cdot & \cdot \\ 0 & \cdot & \cdot & \cdot & \cdot & 1 \\ \end{bmatrix} \nonumber \]

Usando la definición de multiplicación matricial, la primera columna de la$\lbrack A\rbrack^{- 1}$ matriz se puede encontrar resolviendo

\[\begin{bmatrix} a_{11} & a_{12} & \cdot & \cdot & a_{1n} \\ a_{21} & a_{22} & \cdot & \cdot & a_{2n} \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot \\ a_{n1} & a_{n2} & \cdot & \cdot & a_{nn} \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ \cdot \\ \cdot \\ a_{n1}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ \cdot \\ \cdot \\ 0 \\ \end{bmatrix} \nonumber \]

De igual manera, se pueden encontrar las otras columnas de la$\lbrack A\rbrack^{- 1}$ matriz cambiando el lado derecho en consecuencia.

Ejemplo 11

La velocidad ascendente del cohete viene dada por

Cuadro 5.2. Datos de velocidad vs tiempo para un cohete
Tiempo,$t$ (s)	Velocidad,$v$ (m/s)
\ (t\) (s) ">5	\ (v\) (m/s) ">106.8
\ (t\) (s) ">8	\ (v\) (m/s) ">177.2
\ (t\) (s) ">12	\ (v\) (m/s) ">279.2

En un ejemplo anterior, queríamos aproximar el perfil de velocidad por

\[v\left( t \right) = at^{2} + {bt} + c,5 \leq t \leq 12 \nonumber \]

Encontramos que los coeficientes$a,\ b,\ and\ c$ en$v\left( t \right)$ están dados por

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

Primero, encuentra la inversa de

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

y luego usar la definición de inverso para encontrar los coeficientes$a,\ b,\ and\ c.$

Solución

\[\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} a_{11}^{'} & a_{12}^{'} & a_{13}^{'} \\ a_{21}^{'} & a_{22}^{'} & a_{23}^{'} \\ a_{31}^{'} & a_{32}^{'} & a_{33}^{'} \\ \end{bmatrix} \nonumber \]

es la inversa de$\lbrack A\rbrack$, entonces

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} & a_{12}^{'} & a_{13}^{'} \\ a_{21}^{'} & a_{22}^{'} & a_{23}^{'} \\ a_{31}^{'} & a_{32}^{'} & a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \nonumber \]

da tres conjuntos de ecuaciones

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ a_{31}^{'} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix}\begin{bmatrix} a_{13}^{'} \\ a_{23}^{'} \\ a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} \nonumber \]

Resolver los tres conjuntos de ecuaciones anteriores por separado da

\[\begin{bmatrix} a_{11}^{'} \\ a_{21}^{'} \\ a_{31}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.04762 \\ - 0.9524 \\ 4.571 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} - 0.08333 \\ 1.417 \\ - 5.000 \\ \end{bmatrix} \nonumber \]

\[\begin{bmatrix} a_{13}^{'} \\ a_{23}^{'} \\ a_{33}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.03571 \\ - 0.4643 \\ 1.429 \\ \end{bmatrix} \nonumber \]

De ahí

\[\lbrack A\rbrack^{- 1} = \begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix} \nonumber \]

Ahora

\[\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack \nonumber \]

donde

\[\left\lbrack X \right\rbrack = \begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} \nonumber \]

\[\left\lbrack C \right\rbrack = \begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

Usando la definición de$\left\lbrack A \right\rbrack^{- 1},$

\[\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack \nonumber \]

\[\left\lbrack X \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack \nonumber \]

\[\begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix}\begin{bmatrix} 106.8 \\ 177.2 \\ 279.2 \\ \end{bmatrix} \nonumber \]

De ahí

\[\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 0.2905 \\ 19.69 \\ 1.086 \\ \end{bmatrix} \nonumber \]

Entonces

\[v\left( t \right) = 0.2905t^{2} + 19.69t + 1.086,5 \leq t \leq 12 \nonumber \]

¿Hay otra manera de encontrar la inversa de una matriz?

Para encontrar la inversa de matrices pequeñas, la inversa de una matriz invertible se puede encontrar mediante

\[\left\lbrack A \right\rbrack^{- 1} = \frac{1}{\det\left( A \right)}{adj}\left( A \right) \nonumber \]

donde

\[{adj}\left( A \right) = \begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ C_{21} & C_{22} & & C_{2n} \\ \vdots & & & \\ C_{n1} & C_{n2} & \cdots & C_{nn} \\ \end{bmatrix}^{T} \nonumber \]

donde$C_{ij}$ están los cofactores de$a_{ij}$. La matriz

\[\begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1n} \\ C_{21} & C_{22} & \cdots & C_{2n} \\ \vdots & & & \vdots \\ C_{n1} & \cdots & \cdots & C_{nn} \\ \end{bmatrix} \nonumber \]

sí mismo se llama la matriz de cofactores de$[A]$. Los cofactores se definen en el Capítulo 4.

Ejemplo 12

Encuentra la inversa de

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{bmatrix} \nonumber \]

Solución

Del Ejemplo 4.6 en el Capítulo 04.06, encontramos

\[\det\left( A \right) = - 84 \nonumber \]

A continuación tenemos que encontrar el colindante de$\lbrack A\rbrack$. Los cofactores de$A$ se encuentran de la siguiente manera.

El menor de entrada$a_{11}$ es

\[\begin{split} M_{11} &= \left| \begin{matrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{matrix} \right|\\ &= \left| \begin{matrix} 8 & 1 \\ 12 & 1 \\ \end{matrix} \right|\\ &= - 4 \end{split} \nonumber \]

Los cofactores de entrada$a_{11}$ son

\[\begin{split} C_{11} &= \left( - 1 \right)^{1 + 1}M_{11}\\ &= M_{11}\\ &= - 4 \end{split} \nonumber \]

El menor de entrada$a_{12}$ es

\[\begin{split} M_{12} &= \left| \begin{matrix} 25 & 5 & 1 \\ 64 & 8 & 1 \\ 144 & 12 & 1 \\ \end{matrix} \right|\\ &= \left| \begin{matrix} 64 & 1 \\ 144 & 1 \\ \end{matrix} \right|\\ &= - 80 \end{split} \nonumber \]

El cofactor de entrada$a_{12}$ es

\[\begin{split} C_{12} &= \left( - 1 \right)^{1 + 2}M_{12}\\ &= - M_{12}\\ &= - ( - 80)\\ &= 80 \end{split} \nonumber \]

Del mismo modo

\[C_{13} = - 384 \nonumber \]

\[C_{21} = 7 \nonumber \]

\[C_{22} = - 119 \nonumber \]

\[C_{23} = 420 \nonumber \]

\[C_{31} = - 3 \nonumber \]

\[C_{32} = 39 \nonumber \]

\[C_{33} = - 120 \nonumber \]

De ahí que la matriz de cofactores de$\lbrack A\rbrack$ es

\[\left\lbrack C \right\rbrack = \begin{bmatrix} - 4 & 80 & - 384 \\ 7 & - 119 & 420 \\ - 3 & 39 & - 120 \\ \end{bmatrix} \nonumber \]

La unión de la matriz$\lbrack A\rbrack$ es$\lbrack C\rbrack^{T}$,

\[\begin{split} {adj}\left( A \right) &= \left\lbrack C \right\rbrack^{T}\\ &= \begin{bmatrix} - 4 & 7 & - 3 \\ 80 & - 119 & 39 \\ - 384 & 420 & - 120 \\ \end{bmatrix} \end{split} \nonumber \]

De ahí

\[\begin{split} \left\lbrack A \right\rbrack^{- 1} &= \frac{1}{\det\left( A \right)}{adj}\left( A \right)\\ &= \frac{1}{- 84}\begin{bmatrix} - 4 & 7 & - 3 \\ 80 & - 119 & 39 \\ - 384 & 420 & - 120 \\ \end{bmatrix}\\ &= \begin{bmatrix} 0.04762 & - 0.08333 & 0.03571 \\ - 0.9524 & 1.417 & - 0.4643 \\ 4.571 & - 5.000 & 1.429 \\ \end{bmatrix} \end{split} \nonumber \]

Si existe la inversa de una matriz cuadrada [A], ¿es única?

Sí, la inversa de una matriz cuadrada es única, si existe. El comprobante es el siguiente. Supongamos que la inversa de$\lbrack A\rbrack$ es$\lbrack B\rbrack$ y si esta inversa no es única, entonces dejar que otra inversa de$\lbrack A\rbrack$ existir llamada$\lbrack C\rbrack$.

Si$\lbrack B\rbrack$ es la inversa de$\lbrack A\rbrack$, entonces

\[\lbrack B\rbrack\ \lbrack A\rbrack = \lbrack I\rbrack \nonumber \]

Multiplicar ambos lados por$\lbrack C\rbrack$,

\[\lbrack B\rbrack\ \lbrack A\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack\ \lbrack C\rbrack \nonumber \]

\[\lbrack B\rbrack\ \lbrack A\rbrack\ \lbrack C\rbrack = \lbrack C\rbrack \nonumber \]

Dado que$[C]$ es inverso de$\lbrack A\rbrack$,

\[\lbrack A\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack\ \nonumber \]

Multiplicar ambos lados por$\lbrack B\rbrack$,

\[\lbrack B\rbrack\ \lbrack I\rbrack\ = \lbrack C\rbrack \nonumber \]

\[\lbrack B\rbrack\ = \lbrack C\rbrack \nonumber \]

Esto demuestra eso$\lbrack B\rbrack$ y$\lbrack C\rbrack$ son lo mismo. Entonces el inverso de$\lbrack A\rbrack$ es único.

Quiz del Sistema de Ecuaciones

Quiz 1

Una$3 \times 4$ matriz puede tener un rango de como máximo

(A)$3$

(B)$4$

(C)$5$

(D)$12$

Quiz 2

Tres hijos — Jim, Corey y David reciben una herencia de$\text{\$} 2,253,453$. El dinero se pone en tres fideicomisos pero no se divide en partes iguales para empezar. Corey obtiene tres veces lo que recibe David porque Corey hizo una “A” en la clase del Dr. Kaw. Cada fideicomiso se pone en una inversión generadora de intereses. Los tres fideicomisos de Jim, Corey y David pagan intereses de$6\%$,$8\%$,$11\%$, respectivamente. El interés total de los tres fideicomisos combinados al cierre del primer año es$\text{\$}190,740.57$. ¿Cuánto dinero se invirtió en cada fideicomiso? Las ecuaciones en forma de matriz son

(A)$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(B)$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(C)$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ 6 & 8 & 11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

(D)$\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & - 3 \\ .06 & .08 & .11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2253543 \\ 0 \\ 190740.57 \\ \end{bmatrix}$

Quiz 3

¿Cuál de las siguientes matrices no tiene una inversa?

(A)$\begin{bmatrix} 5 & 6 \\ 7 & 8 \\ \end{bmatrix}$

(B)$\begin{bmatrix} 6 & 7 \\ 12 & 14 \\ \end{bmatrix}$

(C)$\begin{bmatrix} 6 & 0 \\ 0 & 7 \\ \end{bmatrix}$

(D)$\begin{bmatrix} 0 & 6 \\ 7 & 0 \\ \end{bmatrix}$

Quiz 4

El conjunto de ecuaciones

\[\begin{bmatrix} 1 & 2 & 5 \\ 2 & 3 & 7 \\ 5 & 8 & 19 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 18 \\ 26 \\ 70 \\ \end{bmatrix} \nonumber \]

tiene

(A) sin solución

(B) número finito de soluciones

(D) infinitas soluciones

Quiz 5

Dado un sistema de$\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \left\lbrack C \right\rbrack$ donde$\left\lbrack A \right\rbrack$ es$n \times n$ matriz y$\left\lbrack X \right\rbrack$ y$\left\lbrack C \right\rbrack$ son$n \times 1$ matrices,$\left\lbrack X \right\rbrack$ existe una solución única si

(A) rango de$\left\lbrack A \right\rbrack =$ rango de$\left\lbrack A \vdots C \right\rbrack$

(B) rango de$\left\lbrack A \right\rbrack =$ rango de$\left\lbrack A \vdots C \right\rbrack = n$

(D) rango de$\left\lbrack A \right\rbrack =$ rango de$\left\lbrack A \vdots C \right\rbrack < n$

Quiz 6

Si$\left\lbrack A \right\rbrack\left\lbrack X \right\rbrack = \begin{bmatrix} - 13 \\ 76 \\ 38 \\ \end{bmatrix}$ y$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} 1 & 2 & - 4 \\ - 8 & 2 & 16 \\ 2 & 4 & 8 \\ \end{bmatrix}$ entonces

(A)$\left\lbrack X \right\rbrack = \begin{bmatrix} -13.000 \\ 864.00 \\ 582.00 \\ \end{bmatrix}$

(B) uno no puede encontrar un único$\left\lbrack X \right\rbrack$.

(C)$\left\lbrack X \right\rbrack = \begin{bmatrix} -1.0000 \\ 2.0000 \\ 4.0000 \\ \end{bmatrix}$

(D) no$\left\lbrack X \right\rbrack$ son posibles soluciones de

Ejercicio de Sistema de Ecuaciones

Ejercicio 1

Para un conjunto de ecuaciones$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack B\rbrack$, existe una solución única si

rango (A) = rango$\left( A\ \vdots\ B \right)$
rango (A) = rango$\left( A\ \vdots\ B \right)$ y rango (A) = número de incógnitas
rango (A) = rango$\left( A\ \vdots\ B \right)$ y rango (A) = número de filas de (A).

Contestar: B

Ejercicio 2

El rango de la matriz

$A = \begin{bmatrix} 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 \\ \end{bmatrix}$es

$1$
$2$
$3$
$4$

Ejercicio 3

Una$3 \times 4$ matriz puede tener un rango de como máximo

$3$
$4$
$5$
$12$

Ejercicio 4

Si$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack C\rbrack$ tiene una solución única, donde el orden de$\lbrack A\rbrack$ es$3 \times 3$,$\lbrack X\rbrack$ es$3 \times 1$, entonces el rango de$\lbrack A\rbrack$ es

$2$
$3$
$4$
$5$

Ejercicio 5

Mostrar si el siguiente sistema de ecuaciones es consistente o inconsistente. Si son consistentes, determinar si la solución sería única o existen infinitas.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 27 \\ \end{bmatrix}$

Contestar: Consistente; Infinitas soluciones

Ejercicio 6

Mostrar si el siguiente sistema de ecuaciones es consistente o inconsistente. Si son consistentes, determinar si la solución sería única o existen infinitas.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 28 \\ \end{bmatrix}$

Contestar: Inconsistente

Ejercicio 7

Mostrar si el siguiente sistema de ecuaciones es consistente o inconsistente. Si son consistentes, determinar si la solución sería única o existen infinitas.

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 13 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 28 \\ \end{bmatrix}$

Contestar: Consistente; Único

Ejercicio 8

El conjunto de ecuaciones

$\begin{bmatrix} 1 & 2 & 5 \\ 7 & 3 & 9 \\ 8 & 5 & 14 \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \\ \end{bmatrix} = \begin{bmatrix} 8 \\ 19 \\ 27 \\ \end{bmatrix}$

tiene

Solución única
Sin solución
Soluciones infinitas

Contestar: C

Ejercicio 9

Para qué valores de$a$ voluntad tendrá la siguiente ecuación

$x_{1} + x_{2} + x_{3} = 4$

$x_{3} = 2$

$\left( a^{2} - 4 \right)x_{1} + x_{3} = a - 2$

Solución única
Sin solución
Soluciones infinitas

Contestar: Si$a \neq + 2 \ \text{or} -2,$ entonces habrá una solución única Si$a = + 2 \ or - 2,$ entonces no habrá solución.
La posibilidad de soluciones infinitas no existe.

Ejercicio 10

Encuentra si

\[\lbrack A\rbrack = \begin{bmatrix} 5 & - 2.5 \\ - 2 & 3 \\ \end{bmatrix} \nonumber \]

\[\lbrack B\rbrack = \begin{bmatrix} 0.3 & 0.25 \\ 0.2 & 0.5 \\ \end{bmatrix} \nonumber \]

son inversas entre sí.

Contestar: Sí

Ejercicio 11

Encuentra si

\[\lbrack A\rbrack = \begin{bmatrix} 5 & 2.5 \\ 2 & 3 \\ \end{bmatrix} \nonumber \]

\[lbrack B\rbrack = \begin{bmatrix} 0.3 & - 0.25 \\ 0.2 & 0.5 \\ \end{bmatrix} \nonumber \]

son inversas entre sí.

Contestar: No

Ejercicio 12

Encuentra el

matriz cofactorial
matriz colindante

\[\left\lbrack A \right\rbrack = \begin{bmatrix} 3 & 4 & 1 \\ 2 & - 7 & - 1 \\ 8 & 1 & 5 \\ \end{bmatrix} \nonumber \]

Contestar: $\begin{bmatrix} - 34 & - 18 & 58 \\ - 19 & 7 & 29 \\ 3 & 5 & - 29 \\ \end{bmatrix}\begin{bmatrix} - 34 & - 19 & 3 \\ - 18 & 7 & 5 \\ 58 & 29 & - 29 \\ \end{bmatrix}$

Ejercicio 13

Encuentra$\lbrack A\rbrack^{- 1}$ usando cualquier método para
$\lbrack A\rbrack = \begin{bmatrix} 3 & 4 & 1 \\ 2 & - 7 & - 1 \\ 8 & 1 & 5 \\ \end{bmatrix}$

Contestar: $\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} 2.931 \times 10^{- 1} & 1.638 \times 10^{- 1} & - 2.586 \times 10^{- 2} \\ 1.552 \times 10^{- 1} & - 6.034 \times 10^{- 2} & - 4.310 \times 10^{- 2} \\ - 5.000 \times 10^{- 1} & - 2.500 \times 10^{- 1} & 2.500 \times 10^{- 1} \\ \end{bmatrix}$

Ejercicio 14

Demostrar que si$\lbrack A\rbrack$ y$\lbrack B\rbrack$ son ambos invertibles y son matrices cuadradas del mismo orden, entonces

\[(\lbrack A\rbrack\lbrack B\rbrack)^{- 1} = \lbrack B\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1} \nonumber \]

Contestar

\[\left( \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \right)^{- 1} = \left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1} \nonumber \]

Let\[\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\begin{split} \left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1} &= \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\\ &= \left\lbrack A \right\rbrack\left\lbrack I \right\rbrack\\ &= \left\lbrack A \right\rbrack \end{split} \nonumber \]

Nuevamente

$\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack$

\[\begin{split} \left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack &= \left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\\ &= \left\lbrack I \right\rbrack\left\lbrack B \right\rbrack\\ &= \left\lbrack B \right\rbrack \end{split} \nonumber \]

Entonces

\[\left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1} = \left\lbrack A \right\rbrack ;\;\;\;\;\;\;\ (1) \nonumber \]

\[\left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack = \left\lbrack B \right\rbrack;\;\;\;\;\;\;\ (2) \nonumber \]

De (1) y (2)

\[\left\lbrack C \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack C \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack B \right\rbrack \nonumber \]

\[\left\lbrack B^{- 1} \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack B \right\rbrack^{- 1}\left\lbrack B \right\rbrack \nonumber \]\[\left\lbrack B \right\rbrack^{- 1}\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack I \right\rbrack. \nonumber \]

Ejercicio 15

¿Cuál es la inversa de una matriz diagonal cuadrada? ¿Siempre existe?

Contestar: Pista: Inverso de un cuadrado n$\times$ n diagonal matriz$\left\lbrack A \right\rbrack$ es$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} \frac{1}{a_{11}} & 0 & \cdots & 0 \\ 0 & \frac{1}{a_{22}} & \cdots & 0 \\ 0 & & & \vdots \\ \vdots & \cdots & \cdots & \frac{1}{a_{nn}} \\ \end{bmatrix}$
Así inversa existe sólo si$a_{ii} \neq 0$ para todos$i$.

Ejercicio 16

$\lbrack A\rbrack$y$\lbrack B\rbrack$ son matrices cuadradas. Si$\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack 0\rbrack$ y$\lbrack A\rbrack$ es invertible, mostrar$\lbrack B\rbrack = 0$.

Contestar: \[\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack 0 \right\rbrack \nonumber \]\[\left\lbrack A^{- 1} \right\rbrack\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack = \left\lbrack A \right\rbrack^{- 1}\left\lbrack 0 \right\rbrack \nonumber \]

Ejercicio 17

Si$\lbrack A\rbrack\ \lbrack B\rbrack\ \lbrack C\rbrack = \lbrack I\rbrack$, donde$\lbrack A\rbrack$,$\lbrack B\rbrack$ y$\lbrack C\rbrack$ son del mismo tamaño, muestran que$\lbrack B\rbrack$ es invertible.

Contestar: Pista:$det({AB}) = det(A)det(B)$

Ejercicio 18

Demostrar si$\lbrack B\rbrack$ es invertible,$\lbrack A\rbrack\ \lbrack B\rbrack^{- 1} = \lbrack B\rbrack^{- 1}\lbrack A\rbrack$ si y solo si$\lbrack A\rbrack\ \lbrack B\rbrack = \lbrack B\rbrack\lbrack A\rbrack$

Contestar: Pista: Multiplicar por$\left\lbrack B \right\rbrack^{- 1}$ en ambos lados,$\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack\left\lbrack B \right\rbrack^{- 1} = \left\lbrack B \right\rbrack^{- 1}\left\lbrack A \right\rbrack\left\lbrack B \right\rbrack^{- 1}$

Ejercicio 19

Para
$\left\lbrack A \right\rbrack = \begin{bmatrix} 10 & - 7 & 0 \\ - 3 & 2.099 & 6 \\ 5 & - 1 & 5 \\ \end{bmatrix}$
$\left\lbrack A \right\rbrack^{- 1} = \begin{bmatrix} - 0.1099 & - 0.2333 & 0.2799 \\ - 0.2999 & - 0.3332 & 0.3999 \\ 0.04995 & 0.1666 & 6.664 \times 10^{- 5} \\ \end{bmatrix}$
Show

\[{det }\left( A \right) = \frac{1}{{det}\left( A^{- 1} \right)}. \nonumber \]

Ejercicio 20

Para qué valores de$a$ tiene el sistema lineal

\[\begin{matrix} x + y = 2 \\ 6x + 6y = a \\ \end{matrix} \nonumber \]

infinitas soluciones
solución única

Contestar

A.$12$

B. no es posible

Ejercicio 21

Tres hijos - Jim, Corey y David reciben una herencia de$\$2,\$253,\$453$. El dinero se pone en tres fideicomisos pero no se divide en partes iguales para empezar. Corey obtiene tres veces más que David porque Corey hizo una “A” en la clase del Dr. Kaw. Cada fideicomiso se pone en una inversión generadora de intereses. Los tres fideicomisos de Jim, Corey y David pagan un interés de$6\%, 8\%, 11\%,$ respectivamente. El interés total de los tres fideicomisos combinados al cierre del primer año es$\$190,\$740.57$. ¿Cuánto dinero se invirtió en cada fideicomiso? Establezca lo siguiente como ecuaciones en forma de matriz. Identificar las incógnitas. No resuelvas por las incógnitas.

Contestar

$J + C + D = \$2,\$253,\$453$

\[C = 3D \nonumber \]

\[0.06J+0.08C+0.11D = \$190,740.57 \nonumber \]En forma de matriz

\[\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & - 3 \\ 0.06 & 0.08 & 0.11 \\ \end{bmatrix}\begin{bmatrix} J \\ C \\ D \\ \end{bmatrix} = \begin{bmatrix} 2,253,453 \\ 0 \\ 190,740.57 \\ \end{bmatrix} \nonumber \]

Ejercicio 22

¿Cuál es el rango de

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}? \nonumber \]

Justifica tu respuesta.

Contestar: En la matriz anterior, 2 (Fila 1) + Fila 2 = Fila 3. De ahí que el rango sea menor a 3. La fila 1 y la fila 2 son linealmente independientes. De ahí que el rango de la matriz sea 2.

Ejercicio 23

¿Cuál es el rango de

\[\begin{bmatrix} 1 & 2 & 3 & 6 \\ 4 & 6 & 7 & 17 \\ 6 & 10 & 13 & 29 \\ \end{bmatrix}? \nonumber \]

Justifica tu respuesta.

Contestar

El determinante de todas las$3 \times 3$ submatrices es cero. De ahí que el rango sea menor a 3. Determinante de

\[\begin{bmatrix} 2 & 3 \\ 6 & 7 \\ \end{bmatrix} = - 4 \neq 0. \nonumber \]

Ejercicio 24

¿Cuál es el rango de

\[\begin{bmatrix} 1 & 2 & 3 & 6 \\ 4 & 6 & 7 & 18 \\ 6 & 10 & 13 & 30 \\ \end{bmatrix}? \nonumber \]

Justifica tu respuesta.

Contestar

En la matriz anterior, 2 (Fila 1) + Fila 2 = Fila 3. Por lo tanto, el rango es menor a 3 ya que las 3 filas son linealmente dependientes. Determinante de

\[\begin{bmatrix} 2 & 3 \\ 6 & 7 \\ \end{bmatrix} = - 4 \neq 0. \nonumber \]

De ahí que el rango sea$2$.

Ejercicio 25

¿Cuántas soluciones tiene el siguiente sistema de ecuaciones?

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 17 \\ 29 \\ \end{bmatrix}? \nonumber \]

Justifica tu respuesta.

Contestar: Rango de $ A = 2$\ Rango de$A|C = 2$\ Número de incógnitas =$3.$\ Hay infinitas soluciones ya que el rango de A es menor que el número de incógnitas.

Ejercicio 26

¿Cuántas soluciones tiene el siguiente sistema de ecuaciones?

\[\begin{bmatrix} 1 & 2 & 3 \\ 4 & 6 & 7 \\ 6 & 10 & 13 \\ \end{bmatrix}\begin{bmatrix} a \\ b \\ c \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 18 \\ 30 \\ \end{bmatrix}? \nonumber \]

Justifica tu respuesta.

Contestar: Rango de$A = 2$\ Rango de$A|C = 2$\ Número de incógnitas =$3.$\ Hay infinitas soluciones ya que el rango de A es menor que el número de incógnitas.

Ejercicio 27

Por cualquier método científico, encuentra la segunda columna de la inversa de

\[\begin{bmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 0 & 0 & 13 \\ \end{bmatrix}. \nonumber \]

Contestar

$\begin{bmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 0 & 0 & 13 \\ \end{bmatrix}\begin{bmatrix} X & a_{12}^{'} & X \\ X & a_{22}^{'} & X \\ X & a_{32}^{'} & X \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$

\[\begin{matrix} a_{12}^{'} + 2a_{22}^{'} = 0 \\ 4a_{12}^{'} + 5a_{22}^{'} = 1 \\ 13a_{32}^{'} = 0 \\ \end{matrix} \nonumber \]

Simplificando,

\[\begin{bmatrix} a_{12}^{'} \\ a_{22}^{'} \\ a_{32}^{'} \\ \end{bmatrix} = \begin{bmatrix} 0.667 \\ - 0.333 \\ 0 \\ \end{bmatrix} \nonumber \]

Ejercicio 28

Simplemente escriba la inversa de (sin necesidad de mostrar ningún trabajo)

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 5 \\ \end{bmatrix} \nonumber \]

Contestar: $\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{1}{2} & 0 & 0 \\ 0 & 0 & \frac{1}{4} & 0 \\ 0 & 0 & 0 & \frac{1}{5} \\ \end{bmatrix}$

Ejercicio 29

Resolver$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack B\rbrack$ por$\lbrack X\rbrack\ $ si

\[\lbrack A\rbrack^{- 1} = \begin{bmatrix} 10 & - 7 & 0 \\ 2 & 2 & 5 \\ 2 & 0 & 6 \\ \end{bmatrix} \nonumber \]

\[\lbrack B\rbrack = \begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix} \nonumber \]

Contestar: \[\begin{split} \lbrack X\rbrack = \lbrack A\rbrack - 1\lbrack B\rbrack\ &= \begin{bmatrix} 10 & - 7 & 0 \\ 2 & 2 & 5 \\ 2 & 0 & 6 \\ \end{bmatrix}\begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix}\\ &=\begin{bmatrix} 52.5 \\ 49.06 \\ 50.072 \\ \end{bmatrix} \end{split} \nonumber \]

Ejercicio 30

$\lbrack A\rbrack\ $Déjese ser una$3 \times 3$ matriz. Supongamos

\[\lbrack X\rbrack = \begin{bmatrix} 7 \\ 2.5 \\ 6.012 \\ \end{bmatrix} \nonumber \]

es una solución al conjunto homogéneo de ecuaciones$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$ (el lado derecho es un vector de orden cero$3 \times 1$). ¿$\lbrack A\rbrack$Tiene un inverso? Justifica tu respuesta.

Contestar

Dado

$\lbrack A\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$
Si$\lbrack A\rbrack^{- 1}$ existe, entonces
$\lbrack A\rbrack^{- 1}\ \lbrack A\rbrack\ \lbrack X\rbrack = \lbrack A\rbrack^{- 1}\lbrack 0\rbrack$
$\lbrack I\rbrack\ \lbrack X\rbrack = \lbrack 0\rbrack$
$\lbrack X\rbrack = \lbrack 0\rbrack$
Esto contradice el valor dado de$\lbrack X\rbrack$. De ahí$\lbrack A\rbrack^{- 1}$ que no exista.

Ejercicio 31

Es el conjunto de vectores

\[\overrightarrow{A} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix},\overrightarrow{B} = \begin{bmatrix} 1 \\ 2 \\ 5 \\ \end{bmatrix},\overrightarrow{C} = \begin{bmatrix} 1 \\ 4 \\ 25 \\ \end{bmatrix} \nonumber \]

linealmente independiente? Justifica tu respuesta.

Contestar: El conjunto de vectores son linealmente independientes.

Ejercicio 32

Cuál es el rango del conjunto de vectores

Justifica tu respuesta.

Contestar: Dado que, los$3$ vectores son linealmente independientes como se demostró anteriormente, el rango de los 3 vectores es$3$.

Ejercicio 33

¿Cuál es el rango de

\[\overrightarrow{A} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix},\overrightarrow{B} = \begin{bmatrix} 2 \\ 2 \\ 4 \\ \end{bmatrix},\overrightarrow{C} = \begin{bmatrix} 3 \\ 3 \\ 5 \\ \end{bmatrix}? \nonumber \]

Justifica tu respuesta.

Contestar: Por inspección,$\overrightarrow{C} = \overrightarrow{A} + \overrightarrow{B}$. Por lo tanto, los 3 vectores son linealmente dependientes, y el rango es menor que 3. Combinación lineal de$\overrightarrow{A}\text{and}\ \overrightarrow{B}$, es decir,$K_{1}\overrightarrow{A} + K_{2}\overrightarrow{B} = 0$ tiene una sola solución K ₁ = K ₂ = 0. Por lo tanto, el rango es 2.