9.2: Normas

Última actualización
Guardar como PDF

Page ID: 115066

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

{{Template.dropdown {ruta:” /álgebra/linear_álgebra "}}}

La norma de un vector en un espacio de producto interno arbitrario es el análogo de la longitud o magnitud de un vector en\(\mathbb{R}^{n}\). Formalmente definimos este concepto de la siguiente manera.

Definición 9.2.1. Dejar\(V \) ser un espacio vectorial sobre\(\mathbb{F}\). Un mapa
\ begin {equation*}
\ begin {split}
\ norm {\ cdot}: V &\ to\ mathbb {R}\\
v &\ mapsto\ norm {v}
\ end {split}
\ end {equation*}
es una norma sobre\(V \) si los tres siguientes se satisfacen las condiciones.

Definición positiva:\(\norm{v}=0 \) si y solo si\(v=0\);
Homogeneidad Positiva:\(\norm{av}=|a|\,\norm{v} \) para todos\(a\in \mathbb{F} \) y\(v\in V\);
Desigualdad triangular:\(\norm{v+w}\le \norm{v}+\norm{w} \) para todos\(v,w\in V\).

Observación 9.2.2. Tenga en cuenta que, de hecho,\(\norm{v}\ge 0 \) para cada uno\(v\in V \) desde

\[ 0 = \norm{v-v} \le \norm{v} + \norm{-v} = 2\norm{v}. \]

A continuación queremos demostrar que una norma siempre se puede definir a partir de un producto interno\(\inner{\cdot}{\cdot} \) a través de la fórmula

\[ \norm{v} = \sqrt{\inner{v}{v}} ~\text{for all} ~ v \in V . \tag{9.2.1} \]

Propiedades 1 y 2 siguen fácilmente desde Condiciones~1 y 3 de Definición~9.1.1. La desigualdad triangular requiere pruebas más cuidadosas, sin embargo, que damos en Teoremo~9.3.4\ ref {thm:triángulo} en el siguiente capítulo.

Si tomamos\(V=\mathbb{R}^n\), entonces la norma definida por el producto puntual habitual se relaciona con la noción habitual de longitud de un vector. A saber, para\(v=(x_1,\ldots,x_n)\in \mathbb{R}^n\), tenemos
\ begin {ecuación}\ label {eqn:NorminRn}
\ norm {v} =\ sqrt {x_1^2+\ cdots + x_n^2}. \ tag {9.2.2}
\ fin {ecuación}

Esto lo ilustramos para el caso de\(\mathbb{R^3} \) la Figura 9.2.1.

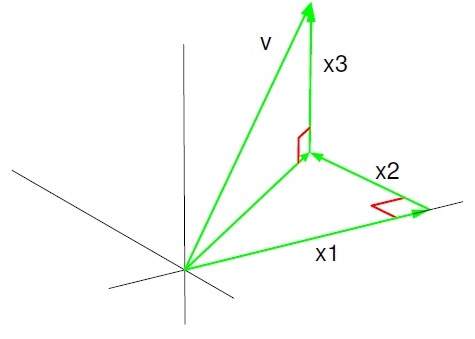
Figura 9.2.1: La longitud de un vector en la ecuación de\( \mathbb{R^3} \) vía 9.2.1.

Si bien siempre es posible comenzar con un producto interno y usarlo para definir una norma, lo contrario requiere más cuidado. En particular, se puede probar que una norma puede ser utilizada para definir un producto interno a través de la Ecuación 9.2.1 si y solo si la norma satisface la Ley del Paralelogramo (Teorema 9.3.6~\ ref {THM:ParallelogramLaw}).

Template:Shilling