9.3: Ortogonalidad

{{Template.dropdown {ruta:” /álgebra/linear_álgebra "}}}

Usando el producto interno, ahora podemos definir la noción de ortogonalidad, probar que el teorema de Pitágoras se mantiene en cualquier espacio interno del producto, y usar la desigualdad Cauchy-Schwarz para probar la desigualdad del triángulo. En particular, esto demostrará que\(\norm{v}=\sqrt{\inner{v}{v}}\) does indeed define a norm.

Definición 9.3.1. Dos vectores\(u,v\in V \) son ortogonales (denotados\(u\bot v\)) si\(\inner{u}{v}=0\).

Tenga en cuenta que el vector cero es el único vector que es ortogonal a sí mismo. De hecho, el vector cero es ortogonal a cada vector\(v\in V\).

Teorema 9.3.2. (Teorema de Pitágoras). Si\(u,v\in V\), un espacio interno del producto, con\(u\bot v\), entonces\(\norm{\cdot} \) definido por\(\norm{v}:=\sqrt{\inner{v}{v}} \) obedece

\[ \norm{u+v}^2 = \norm{u}^2 + \norm{v}^2. \]

Comprobante. Supongamos\(u,v\in V \) tal que\(u\bot v\). Entonces
\ comienza {ecuación*}
\ comenzar {dividir}
\ norma {u+v} ^2 &=\ interior {u+v} {u+v}
=\ norma {u} ^2 +\ norma {v} ^2 +\ interior {u} {v} +\ interior {v} {u} {u}\
&=\ norma {u} ^2 +\ norma {v} ^2.
\ end {split}
\ end {ecuación*}

Cabe destacar que lo contrario del Teorema de Pitágoras sostiene para espacios vectoriales reales ya que, en ese caso,\(\inner{u}{v}+\inner{v}{u}=2\mathrm{Re} \inner{u}{v} =0\).

Dados dos vectores\(u,v\in V \) con\(v\neq 0\), podemos descomponernos de manera única\(u \) en dos piezas: una pieza paralela a\(v \) y una pieza ortogonal a\(v\). A esto se le llama descomposición ortogonal. Más precisamente, tenemos
\ begin {equation*}
u=u_1+u_2,
\ end {equation*}
donde\(u_1=a v \) y\(u_2\bot v \) para algún escalar\(a \in \mathbb{F}\). Para obtener tal descomposición, escriba\(u_2=u-u_1=u-av\). Entonces, para\(u_2 \) ser
ortogonales a\(v\), necesitamos
\ comenzar {ecuación*}
0 =\ inner {u-av} {v} =\ inner {u} {v} - a\ norm {v} ^2.
\ end {ecuation*}
Resolviendo para\(a \) rendimientos para\(a=\inner{u}{v}/\norm{v}^2 \) que
\ begin {ecuación}\ label {eq:descomp ortogonal}
u=\ frac {\ inner {u} {v}} {\ norm {v} ^2} v +\ left (u-\ frac {\ inner {u} {v}} {\ norm {v} ^2} v\ right). \ tag {9.3.1}
\ fin {ecuación}

Esta descomposición es particularmente útil ya que nos permite proporcionar una prueba simple de la desigualdad Cauchy-Schwarz.

Teorema 9.3.3 (Desigualdad de Cauchy-Schwarz). Dado cualquiera\(u,v\in V\), tenemos

\[ |\inner{u}{v}| \le \norm{u} \norm{v}. \]

Además, la igualdad se mantiene si y solo si\(u \) y\(v \) son linealmente dependientes, es decir, son múltiplos escalares entre sí.

Comprobante. Si\(v=0\), entonces ambos lados de la desigualdad son cero. De ahí, supongamos que\(v\neq 0\), y consideremos la descomposición ortogonal
\ begin {equation*}
u =\ frac {\ inner {u} {v}} {\ norm {v} ^2} v + w
\ end {ecuación*}
donde\(w\bot v\). Por el teorema de Pitágoras, tenemos
\ begin {equation*}
\ norm {u} ^2 =\ left\ |\ frac {\ inner {u} {v}} {\ norm {v} ^2} v\ right\ |^2 +\ norm {w} ^2
=\ frac {|\ inner {u} {v} |^2} {\ norm {v} ^2} +\ norma {w} ^2\ ge\ frac {|\ interior {u} {v} |^2} {\ norma {v} ^2}.
\ end {equation*}
Multiplicar ambos lados por\(\norm{v}^2 \) y tomar la raíz cuadrada produce entonces la desigualdad Cauchy-Schwarz.
Tenga en cuenta que obtenemos igualdad en los argumentos anteriores si y solo si\(w=0\). Pero, por la Ecuación (9.3.1), esto significa eso\(u \) y\(v \) son linealmente dependientes.

La desigualdad Cauchy-Schwarz tiene muchas pruebas diferentes. Aquí hay otro.

Prueba Alterna del Teorema 9.3.3. Dado\(u,v\in V\), considera el cuadrado norma del vector\(u+r e^{i\theta}v:\)
\ begin {ecuación*}
0\ le\ norm {u+re^ {i\ theta} v} ^2
=\ norm {u} ^2 + r^2\ norm {v} ^2 + 2\ mathrm {Re} (r e^ {i\ theta}\ inner {u} {v}).
\ end {equation*}
Dado que\( \inner{u}{v} \) es un número complejo, uno puede elegir\(\theta \) para que\(e^{i \theta} \inner{u}{v} \) sea real. De ahí que el lado derecho sea una parábola\(a r^2 +b r +c \) con coeficientes reales. Estará por encima del eje real\(ar^2+br+c\ge 0\), es decir, si no tiene ninguna solución real para\(r\). Este es el caso cuando el discriminante satisface\(b^2-4ac\le 0\). En nuestro caso esto significa
\ comenzar {ecuación*}
4 |\ interior {u} {v} |^2 -4\ norma {u} ^2\ norma {v} ^2\ le 0.
\ end {ecuación*}

Además, la igualdad sólo se mantiene si se\(r \) puede elegir de tal manera que\(u+r e^{i\theta} v =0\), lo que significa que\(u \) y\(v \) son múltiplos escalares.

Ahora que hemos probado la desigualdad Cauchy-Schwarz, finalmente somos capaces de verificar la desigualdad triangular. Este es el último paso para demostrar que\(\norm{v}=\sqrt{\inner{v}{v}}\) sí define una norma. Ilustramos la desigualdad triangular en la Figura 9.3.1.

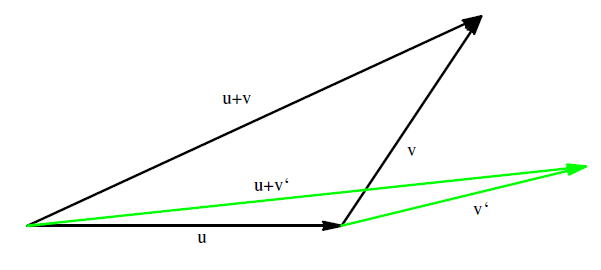
Figura 9.3.1: La desigualdad del triángulo en\( \mathbb{R^2} \)

Teorema 9.3.4. (Desigualdad triangular). Por todo\(u,v\in V \) lo que tenemos

\[ \norm{u+v} \le \norm{u} + \norm{v}. \]

Comprobante. Mediante un cálculo sencillo, obtenemos
\ begin {ecuación*}
\ begin {split}
\ norm {u+v} ^2 &=\ inner {u+v} {u+v} =\ inner {u} {u} +\ inner {v} {v} +\ inner {u} {v} +\
inner {v} {u} {u} {u} v} +\ interior {u} {v} +\ overline {\ interior {u} {v}}
=\ norma {u} ^2 +\ norma {v} ^2 +2\ mathrm {Re}\ interior {u} {v}.
\ end {split}
\ end {ecuación*}
Tenga en cuenta\(\mathrm{Re}\inner{u}{v}\le |\inner{u}{v}| \) que para que, usando la desigualdad Cauchy-Schwarz, obtengamos
\ begin {equation*}
\ norm {u+v} ^2\ le\ norm {u} ^2 +\ norm {v} ^2 + 2\ norm {u}\ norm {v} = (\ norm {u} +\ norm {v}) ^2.
\ end {equation*}
Tomar la raíz cuadrada de ambos lados ahora le da al triángulo desigualdad.

Observación 9.3.5. Obsérvese que la igualdad se mantiene para el triángulo desigualdad si y sólo si\(v=ru \) o\(u=rv \) para algunos\(r\ge 0\). Es decir, la igualdad en la prueba ocurre sólo si\(\inner{u}{v} =\norm{u}\norm{v}\), que es equivalente\(u \) y\(v \) siendo múltiplos escalares entre sí.

Teorema 9.3.6. (Ley de paralelogramo). Dado cualquiera\(u,v\in V\), tenemos
\[ \norm{u+v}^2 + \norm{u-v}^2 = 2(\norm{u}^2 + \norm{v}^2). \]

Comprobante. Por cálculo directo,
\ begin {ecuación*}
\ begin {split}
\ norm {u+v} ^2 +\ norm {u-v} ^2 &=\ inner {u+v} {u+v} +\ inner {u-v} {u-v} {u-v}\\
&=\ norm {u} ^2 +\ norm {v} ^2 +\ inner {u} {v} +\ inner {v} {u} +\ norma {u} ^2 +\ norma {v} ^2
-\ interior {u} {v} -\ interior {v} {u} \\
&=2 (\ norma {u} ^2 +\ norma {v} ^2).
\ end {split}
\ end {ecuación*}

Observación 9.3.7. Ilustramos la ley del paralelogramo en la Figura 9.3.2.

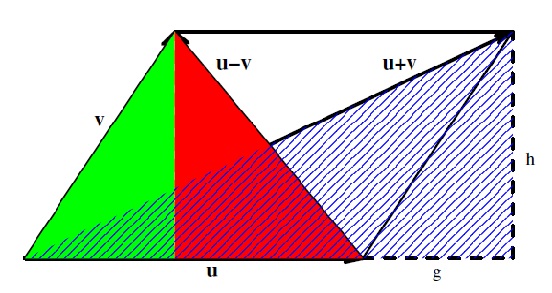
Figura 9.3.2: La ley del paralelogramo en\( \mathbb{R^2} \)

Template:Shilling