5.3: La Transformación Inversa de Laplace

Última actualización
Guardar como PDF

Page ID: 113006

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Por Venir

En La función de transferencia estableceremos que la transformada inversa de Laplace de una función\(h\) es

\[\mathscr{L}^{-1}(h)(t) = \frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{(c+yi)t} h((c+yi)t) dy \nonumber\]

donde\(i \equiv \sqrt{2-1}\) y\(c\) se elige el número real para que todas las singularidades de\(h\) mienten a la izquierda de la línea de integración.

Procediendo con la Transformada Inversa de Laplace

Con la transformada inversa de Laplace se puede expresar la solución de\(\textbf{x}' = B\textbf{x}+\textbf{g}\), como

\[x(t) = \mathscr{L}^{-1} ((sI-B)^{-1}) (\mathscr{L}(\textbf{g}+x(0)) \nonumber\]

Como ejemplo, tomemos el primer componente de\(\mathscr{L}(x)\), a saber

\[\mathscr{L}_{x_{1}} (s) = \frac{0.19(s^2+1.5s+0.27)}{(s+\frac{1}{6})^{4}(s^3+1.655s^2+0.4078s+0.0039)} \nonumber\]

Definimos:

Definición: Pole

También llamadas singularidades, estos son los puntos ss en\(\mathscr{L}_{x_{1}}⁢(s)\) los que estalla.

Estas son claramente las raíces de su denominador, a saber

\[\begin{array}{cccc} {-1/100}&{-329/400 \pm \frac{\sqrt{273}}{16}}&{and}&{-1/6} \end{array} \nonumber\]

Siendo los cuatro negativos, basta con tomar\(c = 0\) y así la integración en Ecuación avanza hacia arriba del eje imaginario. No suponemos que el lector ya se haya encontrado con la integración en el plano complejo pero esperamos que este ejemplo pueda proporcionar la motivación necesaria para una breve visión general de tal. Antes de eso sin embargo observamos que MATLAB ha digerido el cálculo que deseamos desarrollar. Refiriéndose de nuevo a fib3.m para más detalles notamos que el comando ilaplace produce

\[x_{1}(t) = 211.35e^{\frac{-t}{100}}-(0.0554t^3+4.5464t^2+1.085t+474.19)e^{\frac{-t}{6}}+e^{\frac{-(329t)}{400}}(262.842 \cosh (\frac{\sqrt{273}t}{16})) +262.836 \sinh (\frac{\sqrt{273}t}{16})) \nonumber\]

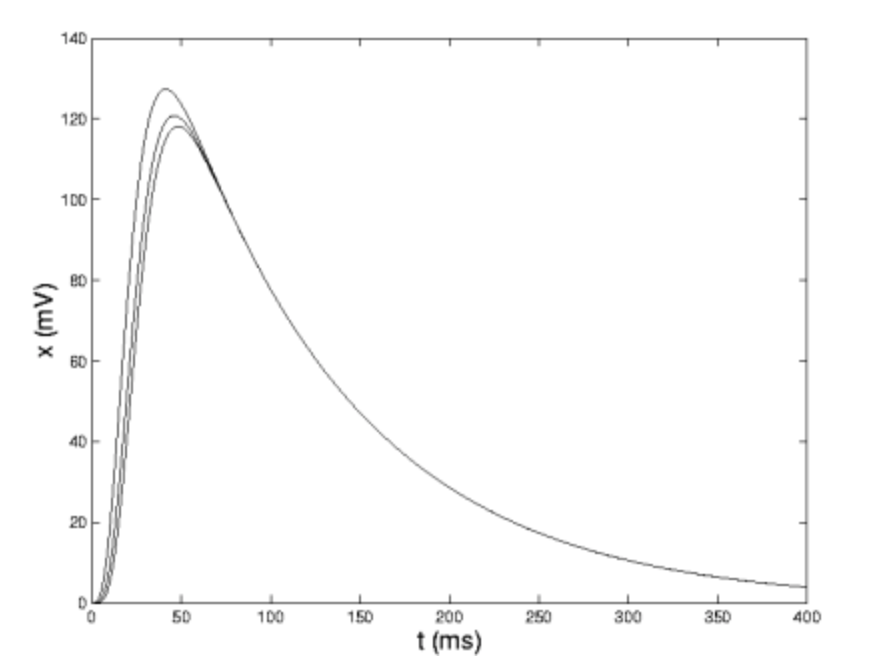
Captura de pantalla 2020-10-04 a las 4.27.22 PM.png — Figura 1. Los 3 potenciales asociados con la figura del modelo de circuito RC.

Los otros potenciales, ver la figura anterior, poseen expresiones similares. Tenga en cuenta que cada uno de los polos de\(\mathscr{L}(⁢x_{1})\) aparecen como exponentes en\(x_{1}\) y que los coeficientes de los exponenciales son polinomios cuyos grados están determinados por el orden del polo respectivo.