7.2: Fórmula Integral de Cauchy

El teorema del residuo

Después del teorema de Cauchy quizás la consecuencia más útil del teorema de Cauchy es el lema de reemplazo de La curva

Supongamos que\(C_{2}\) es una curva cerrada que se encuentra dentro de la región cercada por la curva cerrada\(C_{1}\). Si\(f\) es diferenciable en la región anular exterior\(C_{2}\) e interior\(C_{1}\) entonces

\[\int f(z) dz = \int f(z) dz \nonumber\]

Con referencia a la Figura 1, introducimos dos segmentos verticales y definimos las curvas cerradas\(C_{3} = abcda\) (donde el\(bc\) arco está en el sentido de las agujas del reloj y el\(da\) arco es antihorario) y\(C_{4} = adcba\) (donde el\(ad\) arco es antihorario y el\(cb\) arco es en sentido horario). Por el mero hecho de seguir las flechas aprendemos que

\[\int f(z)dz = \int f(z)dz+\int f(z)dz+\int f(z)dz \nonumber\]

Como el teorema de Cauchy implica que las integrales sobre\(C_{3}\) y\(C_{4}\) cada una desaparecen, tenemos nuestro resultado.

Figura de reemplazo de curva

Figura 1. El lema de reemplazo de la curva

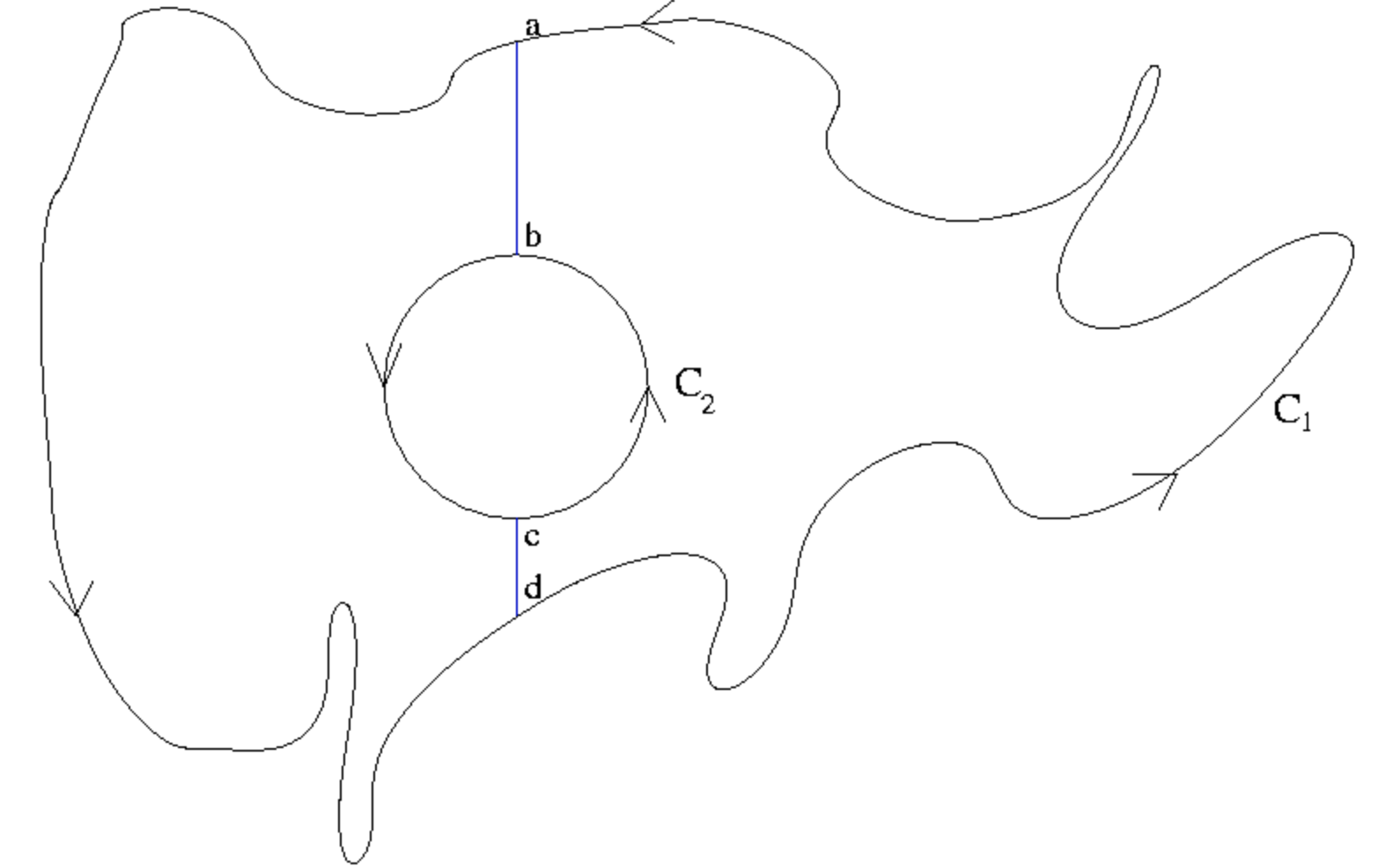
Este lema dice que para integrar una función basta con integrarla sobre regiones donde es singular, es decir, no diferenciable.

Apliquemos este razonamiento a la integral

\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz \nonumber\]

donde\(C\) circunda ambos\(\lambda_{1}\) y\(\lambda_{2}\) como se representa en la Figura. Encontramos que

\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz = \int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz+\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz \nonumber\]

Desarrollando el integrando en fracciones parciales encontramos

\[\begin{align*} \int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz &= \int \frac{\lambda_{1}}{\lambda_{1}-\lambda_{2}}\int \frac{1}{(z-\lambda_{1})} dz+\int \frac{\lambda_{2}}{\lambda_{2}-\lambda_{1}}\int \frac{1}{(z-\lambda_{2})} dz \\[4pt] &= \frac{2\pi i \lambda_{1}}{\lambda_{1}-\lambda_{2}} \end{align*}\]

Del mismo modo,

\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz = \frac{2\pi i \lambda_{1}}{\lambda_{1}-\lambda_{2}} \nonumber\]

Poner las cosas de nuevo juntos encontramos

\[\int \frac{z}{(z-\lambda_{1})(z-\lambda_{2})} dz = 2\pi i \left(\frac{\lambda_{1}}{\lambda_{1}-\lambda_{2}}-\frac{\lambda_{2}}{\lambda_{2}-\lambda_{1}} \right) \nonumber\]

\[= 2 \pi i \nonumber\]

Figura 2. Concentrándose en los postes.

Podemos ver a Ecuación como una instancia especial de integrar una función racional alrededor de una curva que rodea todos los ceros de su denominador. En particular, recordando que el Teorema de Cauchy, encontramos

\[\int q(z) dz = \sum_{j = 1}^{h} \sum_{k = 1}^{m_{j}} \int \frac{q_{j,k}}{(z-\lambda_{j})^k} dz = 2\pi i \sum_{j = 1}^{h} q_{j,1} \nonumber\]

Para tomar un ejemplo un poco más complicado vamos a integrar\(\frac{f(z)}{z-a}\) sobre alguna curva cerrada\(C\) dentro de la cual\(f\) es diferenciable y\(a\) reside. Nuestro lema de reemplazo de curva ahora nos permite afirmar que

\[\int \frac{f(z)}{z-a} dz = \int \frac{f(z)}{z-a} dz \nonumber\]

Parece que no se puede ir más lejos sin especificar\(f\). El lector alerta sin embargo reconoce que en la integral sobre\(C(a,r)\) es independiente de rr y así procede a dejar\(r \rightarrow 0\), en cuyo caso\(z \rightarrow a\) y\(f(z) \rightarrow f(a)\). Computando la integral de en el\(\frac{1}{z-a}\) camino nos lleva a la esperanza de que

\[\int \frac{f(z)}{z-a} dz = f(a) 2 \pi i \nonumber\]

En apoyo de esta conclusión observamos que

\[\int \frac{f(z)}{z-a} dz = \int \frac{f(z)}{z-a} dz+\int \frac{f(a)}{z-a} dz-\int \frac{f(a)}{z-a} dz f(a) = f(a) \int \frac{1}{z-a} dz+\int \frac{f(z)-f(a)}{z-a} dz \nonumber\]

Ahora el primer término es\(f(a) 2\pi i\) independientemente de\(r\) mientras, a medida que se acerca\(r \rightarrow 0\) el integrando del segundo término\(\frac{d}{da}f(a)\) y la región de integración se acerca al punto\(a\). Respecto a este segundo término, como el integrando permanece acotado a medida que el perímetro de\(C(a,r)\) se aproxima a cero el valor de la integral debe ser en sí mismo cero. Este resultado se conoce normalmente como

Ecuación Integral de Cauchy

Si\(f\) es diferenciable en y en la curva cerrada\(C\) entonces

\[f(a) = \frac{1}{2\pi i} \int \frac{f(z)}{z-a} dz \nonumber\]

para cada uno un acostado dentro\(C\).

Las consecuencias de tal fórmula van lejos y profundas. Vamos a ahondar en sólo uno o dos. En primer lugar, observamos que, como un no se acuesta\(C\), el lado derecho es una función perfectamente suave de\(a\). De ahí, diferenciando cada lado, encontramos

\[\frac{d}{da} f(a) = \frac{1}{2\pi i} \int \frac{f(z)}{(z-a)^2} dz \nonumber\]

para cada uno un acostado dentro\(C\). Aplicando este razonamiento nn veces llegamos a una fórmula para la n-ésima derivada de\(f\) at\(a\)

\[\frac{d^n}{da^n} f(a) = \frac{n!}{2\pi i} \int \frac{f(z)}{(z-a)^{1+n}} dz \nonumber\]

para cada uno un acostado dentro\(C\). El resultado es que una vez que\(f\) se demuestra que es diferenciable, de hecho debe ser infinitamente diferenciable. Como una simple extensión consideremos

\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz \nonumber\]

donde todavía\(f\) se asume diferenciable en y en\(C\) y que\(C\) rodea a ambos\(\lambda_{1}\) y\(\lambda_{2}\). Por el lema de reemplazo de curva esta integral es la suma

\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz+\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} \nonumber\]

donde\(\lambda_{j}\) ahora yace solo\(C_{j}\). Como\(\frac{f(z)}{z-\lambda_{2}}\) se comporta bien en\(C_{1}\) podemos usar Ecuación para concluir que

\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz = \frac{f(\lambda_{1})}{(\lambda_{1}-\lambda_{2})^2} \nonumber\]

Del mismo modo, como\(\frac{f(z)}{z-\lambda_{1}}\) se comporta bien en\(C_{2}\) podemos usar Ecuación para concluir que

\[\frac{1}{2\pi i} \int \frac{f(z)}{(z-\lambda_{1})(z-\lambda_{2})^2} dz = \frac{d}{da} (\frac{f(a)}{a-\lambda_{1}}) |_{a=\lambda_{2}} \nonumber\]

Estos cálculos se pueden leer como una instancia concreta de

El teorema del residuo

Si\(g\) es un polinomio con raíces\(\{\lambda_{j} | j = \{1, \cdots, h\}\}\) de grado\(\{d_{j} | j = \{1, \cdots, h\}\}\) y\(C\) es una curva cerrada que rodea cada uno de los\(\lambda_{j}\) y\(f\) es diferenciable en y\(C\) entonces

\[\int \frac{f(z)}{g(z)} dz = 2 \pi i \sum_{j = 1}^{h} res(\lambda_{j}) \nonumber\]

donde

\[res(\lambda_{j}) = lim_{z\rightarrow \lambda_{j}} \frac{1}{(d_{j}-1)!} \frac{d^{d_{j}-1} (z-\lambda_{j})^{d_{j}} \frac{f(z)}{g(z)}}{dz^{d_{j}-1}} \nonumber\]

se llama el residuo de\(\frac{f}{g}\) at\(\lambda_{j}\).

Una de las instancias más importantes de este teorema es la fórmula para la Transformada Inversa de Laplace.