1.1: Sistemas de Ecuaciones, Geometría
- Page ID
- 114667
Sistemas de Ecuaciones, Geometría
- Relacionar los tipos de conjuntos de soluciones de un sistema de dos (tres) variables con las intersecciones de líneas en un plano (la intersección de planos en tres espacios)
Como recordarás, ecuaciones lineales como\(2x+3y=6\) pueden ser gráficas como líneas rectas en el plano de coordenadas. Decimos que esta ecuación se encuentra en dos variables, en este caso\(x\) y\(y\). Supongamos que tiene dos ecuaciones de este tipo, cada una de las cuales se puede graficar como una línea recta, y considere la gráfica resultante de dos líneas. ¿Qué significaría si existe un punto de intersección entre las dos líneas? Este punto, que se encuentra en ambas gráficas, da\(x\) y\(y\) valores para los que ambas ecuaciones son verdaderas. En otras palabras, este punto da el par ordenado (\(x,y\)) que satisface ambas ecuaciones. Si el punto\(\left( x, y \right)\) es un punto de intersección, decimos que\(\left( x, y \right)\) es una solución a las dos ecuaciones. En álgebra lineal, a menudo nos preocupa encontrar la (s) solución (s) a un sistema de ecuaciones, si tales soluciones existen. Primero, consideramos representaciones gráficas de soluciones y posteriormente consideraremos los métodos algebraicos para encontrar soluciones.
Al buscar la intersección de dos líneas en una gráfica, pueden surgir varias situaciones. El siguiente cuadro demuestra las posibles situaciones al considerar dos ecuaciones (dos líneas en la gráfica) que involucran dos variables.
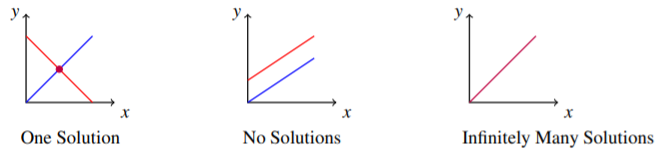
En el primer diagrama, hay un punto de intersección único, lo que significa que solo hay una solución (única) para las dos ecuaciones. En el segundo, no hay puntos de intersección y ninguna solución. Cuando no existe solución, esto significa que las dos líneas son paralelas y nunca se cruzan. La tercera situación que puede ocurrir, como se demuestra en el diagrama tres, es que las dos líneas son realmente la misma línea. Por ejemplo,\(x+y=1\) y\(2x+2y=2\) son ecuaciones que cuando se grafican producen la misma línea. En este caso hay infinitamente muchos puntos que son soluciones de estas dos ecuaciones, ya que cada par ordenado que está en la gráfica de la línea satisface ambas ecuaciones. Al considerar sistemas lineales de ecuaciones, siempre hay tres tipos de soluciones posibles; exactamente una solución (única), infinitamente muchas soluciones, o ninguna solución.
Usa una gráfica para encontrar la solución al siguiente sistema de ecuaciones\[\begin{array}{c} x+y=3 \\ y-x=5 \end{array}\nonumber \]
Solución
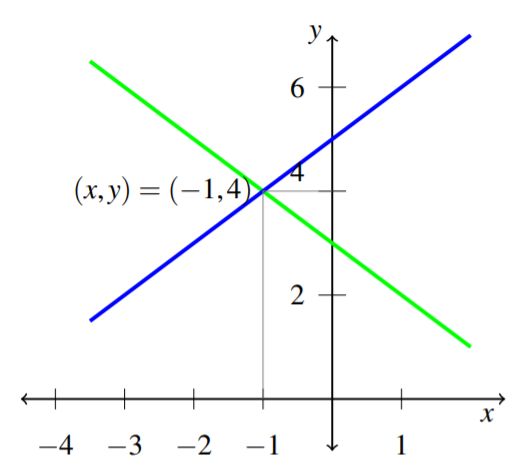
A través de graficar las ecuaciones anteriores e identificar el punto de intersección, podemos encontrar la (s) solución (s). Recuerda que debemos tener o una solución, infinitamente muchas, o ninguna solución en absoluto. En la siguiente gráfica se muestran las dos ecuaciones, así como la intersección. Recuerde, el punto de intersección representa la solución de las dos ecuaciones, o la\(\left( x,y\right)\) que satisface ambas ecuaciones. En este caso, hay un punto de intersección en el\(\left( -1, 4 \right)\) que significa que tenemos una solución única,\(x = -1, y = 4\).
En el ejemplo anterior, investigamos el punto de intersección de dos ecuaciones en dos variables,\(x\) y\(y\). Ahora consideraremos las soluciones gráficas de tres ecuaciones en dos variables.
Considerar un sistema de tres ecuaciones en dos variables. Nuevamente, estas ecuaciones se pueden graficar como líneas rectas en el plano, de manera que la gráfica resultante contenga tres líneas rectas. Recordemos los tres posibles tipos de soluciones; ninguna solución, una solución e infinitamente muchas soluciones. Ahora hay formas más complejas de lograr estas situaciones, debido a la presencia de la tercera línea. Por ejemplo, se puede imaginar el caso de tres líneas de intersección que no tienen un punto de intersección común. Quizás también puedas imaginar tres líneas que se cruzan que sí se cruzan en un solo punto. Estas dos situaciones se ilustran a continuación.
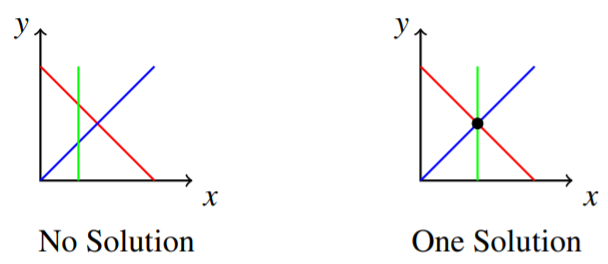
Considera la primera imagen de arriba. Si bien las tres líneas se cruzan entre sí, no hay un punto común de intersección donde las tres líneas se encuentran en un punto. De ahí que no haya solución a las tres ecuaciones. Recuerde, una solución es un punto\(\left( x, y \right)\) que satisface las tres ecuaciones. En el caso de la segunda imagen, las líneas se cruzan en un punto común. Esto significa que hay una solución a las tres ecuaciones cuyas gráficas son las líneas dadas. Deberías tomarte un momento para dibujar la gráfica de un sistema que da como resultado tres líneas paralelas. A continuación, prueba la gráfica de tres líneas idénticas. ¿Qué tipo de solución se representa en cada una de estas gráficas?
Ahora hemos considerado las soluciones gráficas de sistemas de dos ecuaciones en dos variables, así como tres ecuaciones en dos variables. Sin embargo, no hay razón para limitar nuestra investigación a ecuaciones en dos variables. Ahora consideraremos ecuaciones en tres variables.
Tal vez recuerdes que las ecuaciones en tres variables, como\(2x+4y-5z=8\), forman un plano. Arriba, buscábamos intersecciones de líneas con el fin de identificar cualquier solución posible. Al resolver gráficamente sistemas de ecuaciones en tres variables, buscamos intersecciones de planos. Estos puntos de intersección dan los\(\left( x, y, z \right)\) que satisfacen todas las ecuaciones del sistema. ¿Qué tipos de soluciones son posibles cuando se trabaja con tres variables? Considera la siguiente imagen que involucra dos planos, los cuales están dados por dos ecuaciones en tres variables.
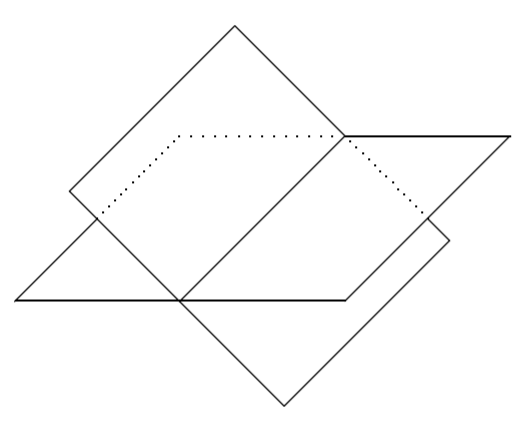
Observe cómo estos dos planos se cruzan en una línea. Esto significa que los puntos\(\left( x,y,z\right)\) en esta línea satisfacen ambas ecuaciones en el sistema. Dado que la línea contiene infinitamente muchos puntos, este sistema tiene infinitamente muchas soluciones.
También podría suceder que los dos planos no se crucen. No obstante, ¿es posible que dos planos se crucen en un solo punto? Tómate un momento para intentar dibujar esta situación, ¡y convencerte de que no es posible! Esto significa que cuando solo tenemos dos ecuaciones en tres variables, ¡no hay manera de tener una solución única! De ahí que los tipos de soluciones posibles para dos ecuaciones en tres variables no sean solución o infinitamente muchas soluciones.
Ahora imagina agregar un tercer plano. Es decir, considerar tres ecuaciones en tres variables. ¿Qué tipos de soluciones son ahora posibles? Considera el siguiente diagrama.
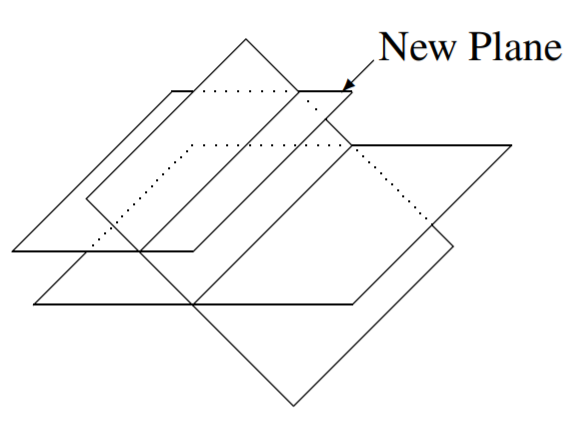
En este diagrama, no hay ningún punto que yace en los tres planos. No hay intersección entre todos los planos así que no hay solución. La imagen ilustra la situación en la que la línea de intersección del nuevo plano con uno de los planos originales forma una línea paralela a la línea de intersección de los dos primeros planos. Sin embargo, en tres dimensiones, es posible que dos líneas no se crucen aunque no sean paralelas. Tales líneas se llaman líneas sesgadas.
Recordemos que al trabajar con dos ecuaciones en tres variables, no fue posible tener una solución única. ¿Es posible al considerar tres ecuaciones en tres variables? De hecho, es posible, y demostramos esta situación en el siguiente cuadro.
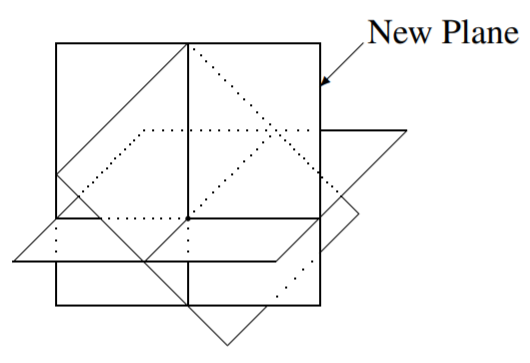
En este caso, los tres planos tienen un único punto de intersección. ¿Se te ocurren otros tipos de soluciones posibles? Otra es que los tres planos podrían cruzarse en una línea, dando como resultado infinitamente muchas soluciones, como en el siguiente diagrama.
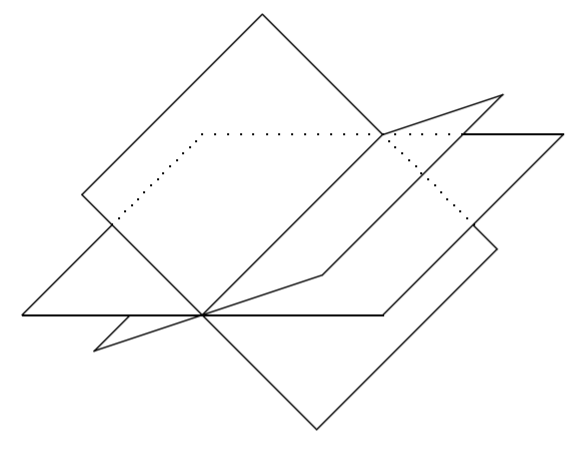
Ahora hemos visto cómo tres ecuaciones en tres variables no pueden tener solución, una solución única, o cruzarse en una línea dando como resultado infinitamente muchas soluciones. También es posible que las tres ecuaciones grafiquen el mismo plano, lo que también lleva a infinitamente muchas soluciones.
Se puede ver que al trabajar con ecuaciones en tres variables, hay muchas más formas de lograr los diferentes tipos de soluciones que cuando se trabaja con dos variables. Puede resultar esclarecedor pasar tiempo imaginando (y dibujando) muchos escenarios posibles, y deberías tomarte un tiempo para probar algunos.
También deberías tomarte un tiempo para imaginar (y dibujar) gráficas de sistemas en más de tres variables. Ecuaciones como\(x+y-2z+4w=8\) con más de tres variables a menudo se denominan hiperplanos. ¡Pronto te darás cuenta de que es complicado dibujar las gráficas de los hiperplanos! A través de las herramientas del álgebra lineal, podemos examinar algebraicamente este tipo de sistemas que son difíciles de graficar. En la siguiente sección, consideraremos estas herramientas algebraicas.
Gráficamente, encontrar el punto\((x_1,y_1)\) que se encuentra en ambas líneas,\(x+3y=1\) y\(4x-y=3\). Es decir, graficar cada línea y ver dónde se cruzan.
Gráficamente, encontrar el punto de intersección de las dos líneas,\(3x+y=3\) y\(x+2y=1\). Es decir, graficar cada línea y ver dónde se cruzan
Tienes un sistema de\(k\) ecuaciones en dos variables,\(k ≥ 2\). Explicar el significado geométrico de
- Sin solución.
- Una solución única.
- Un número infinito de soluciones.