1.7: Variables adimensionales
- Page ID
- 114655
En esta sección se muestra cómo se pueden utilizar sistemas de resolución de ecuaciones para determinar las variables adimensionales apropiadas. Es solo una introducción a este tema y considera un ejemplo específico de un ala de avión simple que se muestra a continuación. Asumimos por simplicidad que se trata de un plano plano en ángulo con el viento que sopla contra él con velocidad\(V\) como se muestra.
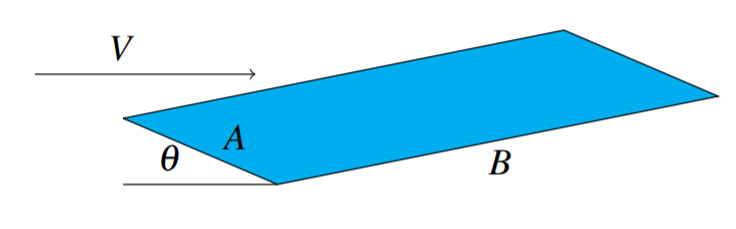
El ángulo\(\theta\) se llama el ángulo de incidencia,\(B\) es la envergadura del ala y\(A\) se llama la cuerda. Denote por\(l\) el ascensor. Entonces esto debería depender de diversas cantidades como\(\theta ,V,B,A\) y así sucesivamente. Aquí hay una tabla en la que se indican diversas cantidades de las que es razonable\(l\) esperar depender.
| Variable | Símbolo | Unidades |
|---|---|---|
| acorde | \(A\) | \(m\) |
| span | \(B\) | \(m\) |
| ángulo de incidencia | \(\theta\) | \(m^0kg^0sec^0\) |
| velocidad del viento | \(V\) | \(m sec^{-1}\) |
| velocidad del sonido | \(V_0\) | \(m sec^{-1}\) |
| densidad del aire | \(\rho\) | \(kgm^{-3}\) |
| viscosidad | \(\mu\) | \(kg sec^{-1}m^{-1}\) |
| ascensor | \(l\) | \(kg sec^{-2}m\) |
Aquí\(m\) denota metros,\(\sec\) se refiere a segundos y\(kg\) se refiere a kilogramos. Todos estos probablemente sean familiares excepto por\(\mu\), que discutiremos con más detalle ahora.
La viscosidad es una medida de la fricción interna que se experimenta cuando el fluido se mueve. Es más o menos una medida de lo “pegajoso” que es el fluido. Considera un pedazo de área paralela a la dirección de movimiento del fluido. Decir que la viscosidad es grande es decir que la fuerza tangencial aplicada a esta zona debe ser grande para lograr un cambio dado de velocidad del fluido en una dirección normal a la fuerza tangencial. Así De\[\mu \left( \text{area}\right) \left( \text{velocity gradient}\right) =\text{ tangential force}\nonumber \] ahí\[\left( \text{units on }\mu \right) m^{2}\left( \frac{m}{\sec m}\right) =kg\sec ^{-2}m\nonumber \] Así las unidades encendidas\(\mu\) son\[kg\sec ^{-1}m^{-1}\nonumber \] como se ha reivindicado anteriormente.
Volviendo a nuestra discusión original, puede pensar que nos gustaría\[l=f\left( A,B,\theta ,V,V_{0},\rho ,\mu \right)\nonumber \] Esto es muy engorroso porque depende de siete variables. Además, es probable que sin mucho cuidado, un cambio en las unidades como pasar de metros a pies resultaría en un valor incorrecto para\(l\). La manera de sortear este problema es buscar\(l\) en función de variables adimensionales multiplicadas por algo que tenga unidades de fuerza. Es útil porque antes que nada, probablemente tendrás menos variables independientes y en segundo lugar, podrías esperar que la fórmula se mantenga independiente de la forma de especificar longitud, masa y así sucesivamente. Se busca\[l=f\left( g_{1},\cdots ,g_{k}\right) \rho V^{2}AB\nonumber \] dónde están las unidades en\(\rho V^{2}AB\) las\[\frac{kg}{m^{3}}\left( \frac{m}{\sec }\right) ^{2}m^{2}=\frac{kg\times m}{ \sec ^{2}}\nonumber \] cuales son las unidades de fuerza. Cada uno de estos\(g_{i}\) es de la forma\[A^{x_{1}}B^{x_{2}}\theta ^{x_{3}}V^{x_{4}}V_{0}^{x_{5}}\rho ^{x_{6}}\mu ^{x_{7}} \label{11julye1f}\] y cada uno\(g_{i}\) es independiente de las dimensiones. Es decir, esta expresión no debe depender de metros, kilogramos, segundos, etc. así, colocando en las unidades para cada una de estas cantidades, se necesita\[m^{x_{1}}m^{x_{2}}\left( m^{x_{4}}\sec ^{-x_{4}}\right) \left( m^{x_{5}}\sec ^{-x_{5}}\right) \left( kgm^{-3}\right) ^{x_{6}}\left( kg\sec ^{-1}m^{-1}\right) ^{x_{7}}=m^{0}kg^{0}\sec ^{0}\nonumber \] Notar que no hay unidades\(\theta\) encendidas porque es solo la medida radián de un ángulo. De ahí que sus dimensiones consisten en longitud dividida por longitud, por lo que es adimensional. Entonces esto lleva a las siguientes ecuaciones para el\(x_{i}.\)
\[\begin{array}{cc} m: & x_{1}+x_{2}+x_{4}+x_{5}-3x_{6}-x_{7}=0 \\ \sec :\ & -x_{4}-x_{5}-x_{7}=0 \\ kg: & x_{6}+x_{7}=0 \end{array}\nonumber \]
La matriz aumentada para este sistema es
\[\left[ \begin{array}{rrrrrrr|r} 1 & 1 & 0 & 1 & 1 & -3 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \end{array} \right]\nonumber \]La forma reducida de fila-escalón viene dada por
\[\left[ \begin{array}{rrrrrrr|r} 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \end{array} \right]\nonumber \]y así las soluciones son de la forma\[\begin{aligned} x_{1} &= -x_{2}-x_{7} \\ x_{3} &= x_{3} \\ x_{4} &= -x_{5}-x_{7} \\ x_{6} &= -x_{7}\end{aligned}\] Así, en términos de vectores, la solución es\[\left[ \begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \\ x_{6} \\ x_{7} \end{array} \right] =\left[ \begin{array}{c} -x_{2}-x_{7} \\ x_{2} \\ x_{3} \\ -x_{5}-x_{7} \\ x_{5} \\ -x_{7} \\ x_{7} \end{array} \right]\nonumber \] Así las variables libres son\(x_{2},x_{3},x_{5},x_{7}.\) Al asignar valores a estas, podemos obtener variables adimensionales colocando los valores obtenidos para el\(x_{i}\) en la fórmula\(\eqref{11julye1f}\). Por ejemplo, let\(x_{2}=1\) y todo el resto de las variables libres son 0. Esto\[x_{1}=-1,x_{2}=1,x_{3}=0,x_{4}=0,x_{5}=0,x_{6}=0,x_{7}=0\nonumber \] rinde La variable adimensional es entonces\(A^{-1}B^{1}\). Esta es la relación entre el span y el acorde. Se llama la relación de aspecto, denotada como\(AR\). Siguiente vamos\(x_{3}=1\) y todos los demás iguales a cero. Esto da para una cantidad adimensional el ángulo\(\theta\). Siguiente vamos\(x_{5}=1\) y todos los demás iguales a cero. Esto da\[x_{1}=0,x_{2}=0,x_{3}=0,x_{4}=-1,x_{5}=1,x_{6}=0,x_{7}=0\nonumber \] Entonces la variable adimensional es\(V^{-1}V_{0}^{1}.\) Sin embargo, se escribe como\(V/V_{0}\). A esto se le llama el número Mach\(\mathcal{M}\). Por último, vamos\(x_{7}=1\) y todas las demás variables libres iguales 0. Entonces\[x_{1}=-1,x_{2}=0,x_{3}=0,x_{4}=-1,x_{5}=0,x_{6}=-1,x_{7}=1\nonumber \] entonces la variable adimensional que resulta de esto es\(A^{-1}V^{-1}\rho ^{-1}\mu .\) Es costumbre escribirla como\(Re=\left( AV\rho \right) /\mu\). A éste se le llama el número de Reynold. Es el que implica viscosidad. Así lo buscaríamos\[l=f\left(Re,AR,\theta ,\mathcal{M}\right) kg\times m/\sec ^{2}\nonumber \] Esto es bastante interesante porque es fácil variar\(Re\) simplemente ajustando la velocidad o\(A\) pero es difícil variar cosas como\(\mu\) o\( \rho\). Tenga en cuenta que todas las cantidades son fáciles de ajustar. Ahora bien, esto podría usarse, junto con experimentos de túnel de viento para obtener una fórmula para el ascensor que sería razonable. También podrías considerar más variables y situaciones más complicadas de la misma manera.


