1.8: Una aplicación a redes de resistencias
- Page ID
- 114668
Las herramientas de álgebra lineal pueden ser utilizadas para estudiar la aplicación de redes de resistencias. A continuación se muestra un ejemplo de circuito eléctrico.
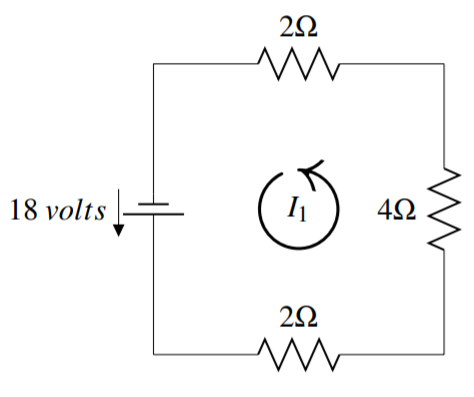
Las líneas dentadas (
) denotan resistencias y los números a su lado dan su resistencia en ohmios, escritos como\(\Omega\). La fuente de voltaje (
) hace que la corriente fluya en la dirección desde la más corta de las dos líneas hacia la más larga (como lo indica la flecha). La corriente para un circuito está etiquetada\(I_k\).
En la figura anterior, la corriente\(I_1\) ha sido etiquetada con una flecha en sentido contrario a las agujas del reloj. Esta es una decisión totalmente arbitraria y podríamos haber optado por etiquetar la corriente en el sentido de las agujas del reloj. Con nuestra elección de dirección aquí, definimos una corriente positiva para fluir en sentido contrario a las agujas del reloj y una corriente negativa para fluir en el sentido de las agujas del reloj.
El objetivo de esta sección es utilizar los valores de resistencias y fuentes de voltaje en un circuito para determinar la corriente. Un teorema esencial para esta aplicación es la ley de Kirchhoff.
La suma de la resistencia (\(R\)) por los amperios (\(I\)) en el sentido contrario a las agujas del reloj alrededor de un bucle es igual a la suma de las fuentes de voltaje (\(V\)) en la misma dirección alrededor del bucle.
La ley de Kirchhoff nos permite establecer un sistema de ecuaciones lineales y resolver cualquier variable desconocida. Al configurar este sistema, es importante rastrear el circuito en sentido contrario a las agujas del reloj. Si se cruza una resistencia o fuente de voltaje contra esta dirección, el término relacionado debe recibir un signo negativo.
Exploraremos esto en el siguiente ejemplo donde determinaremos el valor de la corriente en el diagrama inicial.
Aplicando la Ley de Kirchhoff al diagrama a continuación, determinar el valor para\(I_1\).
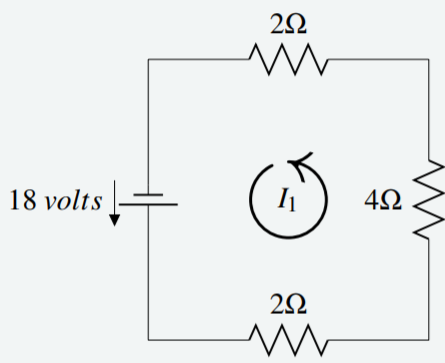
Solución
Comience en la esquina inferior izquierda y trace el circuito en sentido contrario a las agujas del reloj. En la primera resistencia, multiplicando la resistencia y la corriente da\(2I_1\). Continuando de esta manera a través de las tres resistencias da\(2I_1 + 4I_1 + 2 I_1\). Esto debe igualar la fuente de voltaje en la misma dirección. Observe que la dirección de la fuente de voltaje coincide con la dirección contraria a las agujas del reloj especificada, por lo que la tensión es positiva.
Por lo tanto, la ecuación y la solución están dadas por\[\begin{aligned} 2I_1 + 4I_1 + 2 I_1 &= 18 \\ 8I_1 &= 18 \\ I_1 &= \frac{9}{4} A\end{aligned}\]
Dado que la respuesta es positiva, esto confirma que la corriente fluye en sentido contrario a las agujas del reloj.
Aplicando la Ley de Kirchhoff al diagrama a continuación, determinar el valor para\(I_1\).
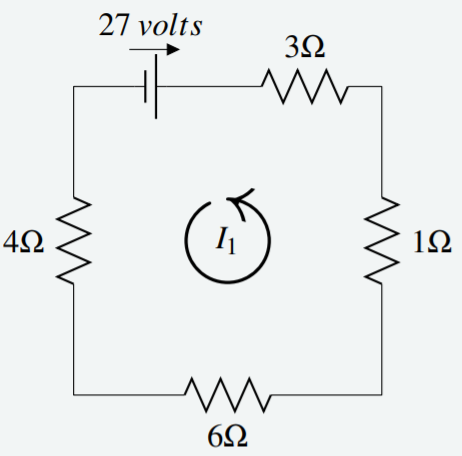
Solución
Comienza en la esquina superior izquierda esta vez, y traza el circuito en sentido contrario a las agujas del reloj. En la primera resistencia, multiplicando la resistencia y la corriente da\(4I_1\). Continuando de esta manera a través de las cuatro resistencias da\(4I_1 + 6I_1 + 1 I_1 + 3I_1\). Esto debe igualar la fuente de voltaje en la misma dirección. Observe que la dirección de la fuente de voltaje es opuesta a la dirección contraria a las agujas del reloj, por lo que la tensión es negativa.
Por lo tanto, la ecuación y la solución están dadas por\[\begin{aligned} 4I_1 + 6I_1 + 1 I_1 + 3I_1&= -27 \\ 14I_1 &= -27 \\ I_1 &= -\frac{27}{14} A\end{aligned}\]
Dado que la respuesta es negativa, esto nos dice que la corriente fluye en sentido horario.
Sigue un ejemplo más complicado. Dos de los circuitos siguientes pueden ser familiares; fueron examinados en los ejemplos anteriores. Sin embargo, como ahora forman parte de un sistema de circuitos más amplio, las respuestas diferirán.
El siguiente diagrama consta de cuatro circuitos. La corriente (\(I_k\)) en los cuatro circuitos se denota por\(I_{1},I_{2},I_{3},I_{4}\). Usando la Ley de Kirchhoff, escribe una ecuación para cada circuito y resuelve para cada corriente.
Solución
Los circuitos se dan en el siguiente diagrama.
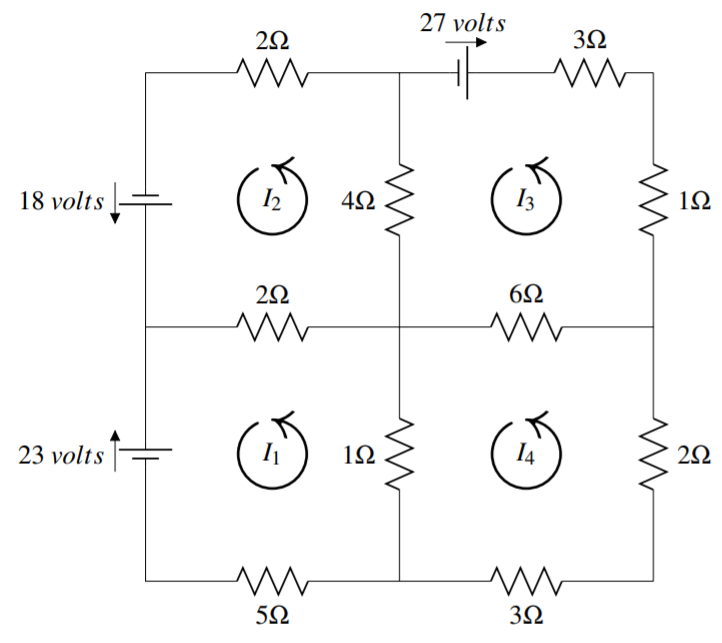
Comenzando por el circuito superior izquierdo, multiplique la resistencia por los amperios y sume los productos resultantes. Específicamente, considere la resistencia etiquetada\(2 \Omega\) que forma parte de los circuitos de\(I_1\) y\(I_2\). Observe que la corriente\(I_2\) corre a través de esto en una dirección positiva (en sentido contrario a las agujas del reloj), y\(I_1\) corre en la dirección opuesta (negativa). El producto de resistencia y amperios es entonces\(2 (I_2 - I_1) = 2I_2 - 2I_1\). Continuar de esta manera para cada resistor, y establecer la suma de los productos igual a la fuente de voltaje para escribir la ecuación:\[2I_{2}-2I_{1}+4I_{2}-4I_{3}+2I_{2}=18\nonumber \] El proceso anterior se utiliza en cada uno de los otros tres circuitos, y las ecuaciones resultantes son:
Circuito superior derecho: Circuito\[4I_{3} - 4I_{2} + 6I_{3} - 6I_{4} + I_{3} + 3I_{3} = -27\nonumber \] inferior derecho: Circuito\[3I_{4} + 2I_{4} + 6I_{4} - 6I_{3} + I_{4} - I_{1} = 0\nonumber \] inferior izquierdo:\[5I_{1}+I_{1}-I_{4}+2I_{1}-2I_{2}=-23\nonumber \]
Observe que el voltaje para los circuitos superior derecho e inferior izquierdo son negativos debido a la dirección de las agujas del reloj que indican.
El sistema resultante de cuatro ecuaciones en cuatro incógnitas es\[\begin{aligned} 2I_{2}-2I_{1}+4I_{2}-4I_{3}+2I_{2}&=18 \\ 4I_{3} - 4I_{2} + 6I_{3} - 6I_{4} + I_{3} + I_{3} &= -27 \\ 2I_{4} + 3I_{4} + 6I_{4} - 6I_{3} + I_{4} - I_{1} &= 0 \\ 5I_{1}+I_{1}-I_{4}+2I_{1}-2I_{2}&= -23\end{aligned}\] Simplificando y reordenando con variables en orden, tenemos:\[\begin{aligned} -2I_{1}+8I_{2}-4I_{3}&=18 \\ - 4I_{2} + 14I_{3} - 6I_{4} &= -27 \\ -I_{1} - 6I_{3} + 12I_{4} &= 0 \\ 8I_{1}-2I_{2} - I_{4} &= -23\end{aligned}\] La matriz aumentada es\[\left[ \begin{array}{rrrr|r} -2 & 8 & -4 & 0 & 18 \\ 0 & -4 & 14 & -6 & -27 \\ -1 & 0 & -6 & 12 & 0 \\ 8 & -2 & 0 & -1 & -23 \end{array} \right]\nonumber \]
La solución a esta matriz es\[\begin{aligned} I_{1} &= -3 A\\ I_{2} &= \frac{1}{4} A\\ I_{3} &= -\frac{5}{2} A\\ I_{4} &= -\frac{3}{2} A\end{aligned}\]
Esto nos dice que las corrientes\(I_1, I_3,\) y\(I_4\) viajan en sentido horario mientras\(I_2\) viaja en sentido antihorario.