1.9: Ejercicios
- Page ID
- 114695
Ejercicios
Gráficamente, encuentra el punto\(\left( x_{1},y_{1}\right)\) que se encuentra en ambas líneas,\(x+3y=1\) y es\(4x-y=3.\) decir, grafica cada línea y mira dónde se cruzan.
- Responder
-
\(\begin{array}{c} x+3y=1 \\ 4x-y=3 \end{array}\), La solución es:\(\left[ x=\frac{10}{13},y=\frac{1}{13}\right]\).
Gráficamente, encuentra el punto de intersección de las dos líneas\(3x+y=3\) y es\(x+2y=1.\) decir, grafica cada línea y mira dónde se cruzan.
- Responder
-
\(\begin{array}{c} 3x+y=3 \\ x+2y=1 \end{array}\), La solución es:\(\left[ x=1,y=0\right]\)
¿Las tres líneas,\(x + 2y = 1\),\(2x − y = 1\), y\(4x + 3y = 3\) tienen un punto común de intersección? Si es así, encuentra el punto y si no, diga por qué no tienen un punto de intersección tan común.
- Responder
-
\(\begin{array}{c}x+2y=1 \\ 2x-y=1\\4x+3y=3\end{array}\), La solución es:\(\left[ x=\frac{3}{5},y=\frac{1}{5}\right]\)
¿Los tres planos,\(x+y−3z = 2\),\(2x+y+z = 1\), y\(3x+2y−2z = 0\) tienen un punto común de intersección? Si es así, encuentra uno y si no, diga por qué no hay tal punto.
- Responder
-
No existe solución. Esto se puede ver escribiendo la matriz aumentada y haciendo operaciones de fila. \(\left[\begin{array}{cccc}1&1&-3&2 \\ 2&1&1&1 \\ 3&2&-2&0\end{array}\right]\), forma de escalón de fila:\(\left[\begin{array}{cccc}1&0&4&0 \\ 0&1&-7&0 \\ 0&0&0&1\end{array}\right]\). Así una de las ecuaciones dice\(0=1\) en un sistema equivalente de ecuaciones.
Cuatro veces el peso de Gastón es\(150\) libras más que el peso de Icabod. Cuatro veces el peso de Icabod es\(660\) libras menos de diecisiete veces el peso de Gastón. Cuatro veces el peso de Gastón más el peso de Siegfried equivale a\(290\) libras. Brunhilde equilibraría a los otros tres. Encuentra los pesos de las cuatro personas.
- Responder
-
\(\begin{array}{c}4g-I=150 \\ 4I-17g=-660 \\ 4g+s=290 \\ g+I+s-b=0\end{array}\), La solución es:\(\left\{ g=60, I=90, b=200, s=50\right\}\)
Considera la siguiente matriz aumentada en la que\(\ast\) denota un número arbitrario y\(\blacksquare\) denota un número distinto de cero. Determinar si la matriz aumentada dada es consistente. Si es consistente, ¿la solución es única? \[\left[ \begin{array}{ccccc|c} \blacksquare & \ast & \ast & \ast & \ast & \ast \\ 0 & \blacksquare & \ast & \ast & 0 & \ast \\ 0 & 0 & \blacksquare & \ast & \ast & \ast \\ 0 & 0 & 0 & 0 & \blacksquare & \ast \end{array} \right]\nonumber \]
- Responder
-
La solución existe pero no es única.
Considera la siguiente matriz aumentada en la que\(\ast\) denota un número arbitrario y\(\blacksquare\) denota un número distinto de cero. Determinar si la matriz aumentada dada es consistente. Si es consistente, ¿la solución es única? \[\left[ \begin{array}{ccc|c} \blacksquare & \ast & \ast & \ast \\ 0 & \blacksquare & \ast & \ast \\ 0 & 0 & \blacksquare & \ast \end{array} \right]\nonumber \]
- Responder
-
Una solución existe y es única.
Considera la siguiente matriz aumentada en la que\(\ast\) denota un número arbitrario y\(\blacksquare\) denota un número distinto de cero. Determinar si la matriz aumentada dada es consistente. Si es consistente, ¿la solución es única? \[\left[ \begin{array}{ccccc|c} \blacksquare & \ast & \ast & \ast & \ast & \ast \\ 0 & \blacksquare & 0 & \ast & 0 & \ast \\ 0 & 0 & 0 & \blacksquare & \ast & \ast \\ 0 & 0 & 0 & 0 & \blacksquare & \ast \end{array} \right]\nonumber \]
Considera la siguiente matriz aumentada en la que\(\ast\) denota un número arbitrario y\(\blacksquare\) denota un número distinto de cero. Determinar si la matriz aumentada dada es consistente. Si es consistente, ¿la solución es única? \[\left[ \begin{array}{ccccc|c} \blacksquare & \ast & \ast & \ast & \ast & \ast \\ 0 & \blacksquare & \ast & \ast & 0 & \ast \\ 0 & 0 & 0 & 0 & \blacksquare & 0 \\ 0 & 0 & 0 & 0 & \ast & \blacksquare \end{array} \right]\nonumber \]
- Responder
-
Podría haber una solución. Si es así, hay infinitamente muchos.
Supongamos que un sistema de ecuaciones tiene menos ecuaciones que variables. ¿Será un sistema así necesariamente consistente? Si es así, explique por qué y si no, dé un ejemplo que no sea consistente.
- Responder
-
No. Considerar\(x+y+z=2\) y\(x+y+z=1.\)
Si un sistema de ecuaciones tiene más ecuaciones que variables, ¿puede tener una solución? Si es así, da un ejemplo y si no, diga por qué no.
- Responder
-
Estos pueden tener una solución. Por ejemplo,\(x+y=1,2x+2y=2,3x+3y=3\) incluso tiene un conjunto infinito de soluciones.
Encontrar\(h\) tal que\[\left[ \begin{array}{rr|r} 2 & h & 4 \\ 3 & 6 & 7 \end{array} \right]\nonumber \] sea la matriz aumentada de un sistema inconsistente.
- Responder
-
\(h=4\)
Encuentra\(h\) tal que\[\left[ \begin{array}{rr|r} 1 & h & 3 \\ 2 & 4 & 6 \end{array} \right]\nonumber \] sea la matriz aumentada de un sistema consistente.
- Responder
-
Cualquiera\(h\) funcionará.
Encuentra\(h\) tal que\[\left[ \begin{array}{rr|r} 1 & 1 & 4 \\ 3 & h & 12 \end{array} \right]\nonumber \] sea la matriz aumentada de un sistema consistente.
- Responder
-
Cualquiera\(h\) funcionará.
Elija\(h\) y\(k\) tal que la matriz aumentada mostrada tenga cada una de las siguientes:
- una solución
- sin solución
- infinitamente muchas soluciones
\[\left[ \begin{array}{rr|r} 1 & h & 2 \\ 2 & 4 & k \end{array} \right]\nonumber \]
- Responder
-
Si\(h\neq 2\) habrá una solución única para alguna\(k\). Si\(h=2\) y no\(k\neq 4,\) hay soluciones. Si\(h=2\) y\(k=4,\) entonces hay infinitamente muchas soluciones.
Elija\(h\) y\(k\) tal que la matriz aumentada mostrada tenga cada una de las siguientes:
- una solución
- sin solución
- infinitamente muchas soluciones
\[\left[ \begin{array}{rr|r} 1 & 2 & 2 \\ 2 & h & k \end{array} \right]\nonumber \]
- Responder
-
Si\(h\neq 4,\) entonces hay exactamente una solución. Si\(h=4\) y\(k\neq 4,\) entonces no hay soluciones. Si\(h=4\) y\(k=4,\) entonces hay infinitamente muchas soluciones.
Determinar si el sistema es consistente. Si es así, ¿la solución es única? \[\begin{array}{c} x+2y+z-w=2 \\ x-y+z+w=1 \\ 2x+y-z=1 \\ 4x+2y+z=5 \end{array}\nonumber \]
- Contestar
-
No hay solución. El sistema es inconsistente. Esto se puede ver desde la matriz aumentada. \(\left[ \begin{array}{rrrrr} 1 & 2 & 1 & -1 & 2 \\ 1 & -1 & 1 & 1 & 1 \\ 2 & 1 & -1 & 0 & 1 \\ 4 & 2 & 1 & 0 & 5 \end{array} \right]\), forma reducida de fila-escalón:\(\left[ \begin{array}{rrrrr} 1 & 0 & 0 & \frac{1}{3} & 0 \\ 0 & 1 & 0 & -\frac{2}{3} & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \right] .\)
Determinar si el sistema es consistente. Si es así, ¿la solución es única? \[\begin{array}{c} x+2y+z-w=2 \\ x-y+z+w=0 \\ 2x+y-z=1 \\ 4x+2y+z=3 \end{array}\nonumber \]
- Contestar
-
La solución es:\(\left[ w=\frac{3}{2}y-1,x=\frac{2}{3}-\frac{1}{2}y,z=\frac{1}{3 }\right]\)
Determinar qué matrices están en forma de fila reducida.
- \(\left[ \begin{array}{rrr} 1 & 2 & 0 \\ 0 & 1 & 7 \end{array} \right]\)
- \(\left[ \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{array} \right]\)
- \(\left[ \begin{array}{rrrrrr} 1 & 1 & 0 & 0 & 0 & 5 \\ 0 & 0 & 1 & 2 & 0 & 4 \\ 0 & 0 & 0 & 0 & 1 & 3 \end{array} \right]\)
- Contestar
-
- Este no lo es.
- Éste es.
- Éste es.
Fila reduce la siguiente matriz para obtener la forma fila-escalón. Después continuar obteniendo la forma de fila-escalón reducida. \[\left[ \begin{array}{rrrr} 2 & -1 & 3 & -1 \\ 1 & 0 & 2 & 1 \\ 1 & -1 & 1 & -2 \end{array} \right]\nonumber \]
Fila reduce la siguiente matriz para obtener la forma fila-escalón. Después continuar obteniendo la forma de fila-escalón reducida. \[\left[ \begin{array}{rrrr} 0 & 0 & -1 & -1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & -1 \end{array} \right]\nonumber \]
Fila reduce la siguiente matriz para obtener la forma fila-escalón. Después continuar obteniendo la forma de fila-escalón reducida. \[\left[ \begin{array}{rrrr} 3 & -6 & -7 & -8 \\ 1 & -2 & -2 & -2 \\ 1 & -2 & -3 & -4 \end{array} \right]\nonumber \]
Fila reduce la siguiente matriz para obtener la forma fila-escalón. Después continuar obteniendo la forma de fila-escalón reducida. \[\left[ \begin{array}{rrrr} 2 & 4 & 5 & 15 \\ 1 & 2 & 3 & 9 \\ 1 & 2 & 2 & 6 \end{array} \right]\nonumber \]
Fila reduce la siguiente matriz para obtener la forma fila-escalón. Después continuar obteniendo la forma de fila-escalón reducida. \[\left[ \begin{array}{rrrr} 4 & -1 & 7 & 10 \\ 1 & 0 & 3 & 3 \\ 1 & -1 & -2 & 1 \end{array} \right]\nonumber \]
Fila reduce la siguiente matriz para obtener la forma fila-escalón. Después continuar obteniendo la forma de fila-escalón reducida. \[\left[ \begin{array}{rrrr} 3 & 5 & -4 & 2 \\ 1 & 2 & -1 & 1 \\ 1 & 1 & -2 & 0 \end{array} \right]\nonumber \]
Fila reduce la siguiente matriz para obtener la forma fila-escalón. Después continuar obteniendo la forma de fila-escalón reducida. \[\left[ \begin{array}{rrrr} -2 & 3 & -8 & 7 \\ 1 & -2 & 5 & -5 \\ 1 & -3 & 7 & -8 \end{array} \right]\nonumber \]
Encuentre la solución del sistema cuya matriz aumentada es\[\left[ \begin{array}{rrr|r} 1 & 2 & 0 & 2 \\ 1 & 3 & 4 & 2 \\ 1 & 0 & 2 & 1 \end{array} \right]\nonumber \]
Encuentre la solución del sistema cuya matriz aumentada es\[\left[ \begin{array}{rrr|r} 1 & 2 & 0 & 2 \\ 2 & 0 & 1 & 1 \\ 3 & 2 & 1 & 3 \end{array} \right]\nonumber \]
- Contestar
-
La forma reducida fila-escalón es\(\left[ \begin{array}{rrr|r} 1 & 0 & \frac{1}{2} & \frac{1}{2} \\ 0 & 1 & -\frac{1}{4} &\frac{3}{4} \\ 0 & 0 & 0 & 0 \end{array} \right] .\) Por lo tanto, la solución es de la forma\(z=t,y=\frac{3}{4}+t\left( \frac{1}{4}\right) ,x=\frac{1}{2}-\frac{1}{2}t\) donde\(t\in \mathbb{R}\).
Encuentre la solución del sistema cuya matriz aumentada es\[\left[ \begin{array}{rrr|r} 1 & 1 & 0 & 1 \\ 1 & 0 & 4 & 2 \end{array} \right]\nonumber \]
- Contestar
-
La forma reducida de fila-escalón es\(\left[ \begin{array}{rrr|r} 1 & 0 & 4 & 2 \\ 0 & 1 & -4 & -1 \end{array} \right]\) y así la solución es\(z=t,y=4t,x=2-4t.\)
Encuentre la solución del sistema cuya matriz aumentada es\[\left[ \begin{array}{rrrrr|r} 1 & 0 & 2 & 1 & 1 & 2 \\ 0 & 1 & 0 & 1 & 2 & 1 \\ 1 & 2 & 0 & 0 & 1 & 3 \\ 1 & 0 & 1 & 0 & 2 & 2 \end{array} \right]\nonumber \]
- Contestar
-
La forma reducida de fila-escalón es\(\left[ \begin{array}{rrrrr|r} 1 & 0 & 0 & 0 & 9 & 3 \\ 0 & 1 & 0 & 0 & -4 & 0 \\ 0 & 0 & 1 & 0 & -7 & -1 \\ 0 & 0 & 0 & 1 & 6 & 1 \end{array} \right]\) y así\(x_{5}=t,x_{4}=1-6t,x_{3}=-1+7t,x_{2}=4t,x_{1}=3-9t\).
Encuentre la solución del sistema cuya matriz aumentada es\[\left[ \begin{array}{rrrrr|r} 1 & 0 & 2 & 1 & 1 & 2 \\ 0 & 1 & 0 & 1 & 2 & 1 \\ 0 & 2 & 0 & 0 & 1 & 3 \\ 1 & -1 & 2 & 2 & 2 & 0 \end{array} \right]\nonumber \]
- Contestar
-
La forma reducida de fila-escalón es\(\left[ \begin{array}{rrrrr|r} 1 & 0 & 2 & 0 & -\frac{1}{2} & \frac{5}{2} \\ 0 & 1 & 0 & 0 & \frac{1}{2} & \frac{3}{2} \\ 0 & 0 & 0 & 1 & \frac{3}{2} & -\frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right]\). Por lo tanto, vamos\(x_{5}=t,x_{3}=s.\) Entonces las otras variables son dadas por\(x_{4}=-\frac{1}{2}-\frac{3}{2}t,x_{2}=\frac{3}{2}-t\frac{1}{2} ,,x_{1}=\frac{5}{2}+\frac{1}{2}t-2s.\)
Encuentre la solución al sistema de ecuaciones,\(7x+14y+15z=22,\)\(2x+4y+3z=5,\) y\(3x+6y+10z=13.\)
- Contestar
-
La solución es:\(\left[ x=1-2t,z=1,y=t\right]\)
Encuentre la solución al sistema de ecuaciones,\(3x-y+4z=6,\)\(y+8z=0,\) y\(-2x+y=-4.\)
- Contestar
-
La solución es:\(\left[ x=2-4t,y=-8t,z=t\right]\)
Encuentre la solución al sistema de ecuaciones,\(9x-2y+4z=-17,\)\(13x-3y+6z=-25,\) y\(-2x-z=3.\)
- Contestar
-
La solución es:\(\left[x=-1,y=2,z=-1\right]\)
Encuentre la solución al sistema de ecuaciones,\(65x+84y+16z=546,\)\(81x+105y+20z=682,\) y\(84x+110y+21z=713.\)
- Contestar
-
La solución es:\(\left[ x=2,y=4,z=5\right]\)
Encuentre la solución al sistema de ecuaciones,\(8x+2y+3z=-3,8x+3y+3z=-1,\) y\(4x+y+3z=-9.\)
- Contestar
-
La solución es:\(\left[ x=1,y=2,z=-5\right]\)
Encuentre la solución al sistema de ecuaciones,\(-8x+2y+5z=18,-8x+3y+5z=13,\) y\(-4x+y+5z=19.\)
- Contestar
-
La solución es:\(\left[x=-1,y=-5,z=4\right]\)
Encuentre la solución al sistema de ecuaciones,\(3x-y-2z=3,\)\(y-4z=0,\) y\(-2x+y=-2.\)
- Contestar
-
La solución es:\(\left[ x=2t+1,y=4t,z=t\right]\)
Encuentre la solución al sistema de ecuaciones,\(-9x+15y=66,-11x+18y=79\),\(-x+y=4\), y\(z=3\).
- Contestar
-
La solución es:\(\left[x=1,y=5,z=3\right]\)
Encontrar la solución al sistema de ecuaciones,\(-19x+8y=-108,\)\(-71x+30y=-404,\)\(-2x+y=-12,\)\(4x+z=14.\)
- Contestar
-
La solución es:\(\left[ x=4,y=-4,z=-2\right]\)
Supongamos que un sistema de ecuaciones tiene menos ecuaciones que variables y ha encontrado una solución a este sistema de ecuaciones. ¿Es posible que tu solución sea la única? Explicar.
- Contestar
-
No. Considerar\(x+y+z=2\) y\(x+y+z=1.\)
Supongamos que un sistema de ecuaciones lineales tiene una matriz\(2\times 4\) aumentada y la última columna es una columna pivote. ¿Podría ser consistente el sistema de ecuaciones lineales? Explicar.
- Contestar
-
No. Esto conduciría a\(0=1.\)
Supongamos que la matriz de coeficientes de un sistema de\(n\) ecuaciones con\(n\) variables tiene la propiedad de que cada columna es una columna pivote. ¿De ello se deduce que el sistema de ecuaciones debe tener una solución? Si es así, ¿la solución debe ser única? Explicar.
- Contestar
-
Sí. Cuenta con una solución única.
Supongamos que hay una solución única a un sistema de ecuaciones lineales. ¿Qué debe ser cierto de las columnas pivotes en la matriz aumentada?
- Contestar
-
La última columna no debe ser una columna pivote. Las columnas restantes deben ser columnas pivotantes.
La temperatura de estado estacionario\(u\),, de una placa resuelve la ecuación de Laplace,\(\Delta u=0.\) Una forma de aproximar la solución es dividir la placa en una malla cuadrada y requerir la temperatura en cada nodo para igualar el promedio de la temperatura en los cuatro nodos adyacentes. En la siguiente imagen, los números representan la temperatura observada en los nodos indicados. Encuentra la temperatura en los nodos interiores, indicados por\(x,y,z,\) y\(w\). Una de las ecuaciones es\(z={0.05in}\frac{1}{4}\left( 10+0+w+x\right)\).
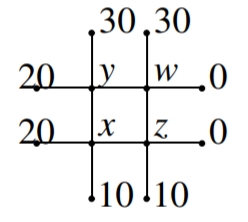
- Contestar
-
Necesitas\(\begin{array}{c} \frac{1}{4}\left( 20+30+w+x\right) -y=0 \\ \frac{1}{4}\left( y+30+0+z\right) -w=0 \\ \frac{1}{4}\left( 20+y+z+10\right) -x=0 \\ \frac{1}{4}\left( x+w+0+10\right) -z=0 \end{array}\), la solución es:\(\left[ w=15,x=15,y=20,z=10\right] .\)
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrr} 4 & -16 & -1 & -5 \\ 1 & -4 & 0 & -1 \\ 1 & -4 & -1 & -2 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrr} 3 & 6 & 5 & 12 \\ 1 & 2 & 2 & 5 \\ 1 & 2 & 1 & 2 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrrr} 0 & 0 & -1 & 0 & 3 \\ 1 & 4 & 1 & 0 & -8 \\ 1 & 4 & 0 & 1 & 2 \\ -1 & -4 & 0 & -1 & -2 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrr} 4 & -4 & 3 & -9 \\ 1 & -1 & 1 & -2 \\ 1 & -1 & 0 & -3 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrrr} 2 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 7 \\ 1 & 0 & 0 & 1 & 7 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrr} 4 & 15 & 29 \\ 1 & 4 & 8 \\ 1 & 3 & 5 \\ 3 & 9 & 15 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrrr} 0 & 0 & -1 & 0 & 1 \\ 1 & 2 & 3 & -2 & -18 \\ 1 & 2 & 2 & -1 & -11 \\ -1 & -2 & -2 & 1 & 11 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrrr} 1 & -2 & 0 & 3 & 11 \\ 1 & -2 & 0 & 4 & 15 \\ 1 & -2 & 0 & 3 & 11 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrr} -2 & -3 & -2 \\ 1 & 1 & 1 \\ 1 & 0 & 1 \\ -3 & 0 & -3 \end{array} \right]\nonumber \]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrrr} 4 & 4 & 20 & -1 & 17 \\ 1 & 1 & 5 & 0 & 5 \\ 1 & 1 & 5 & -1 & 2 \\ 3 & 3 & 15 & -3 & 6 \end{array} \right]\nonumber\]
Encuentra el rango de la siguiente matriz. \[\left[ \begin{array}{rrrrr} -1 & 3 & 4 & -3 & 8 \\ 1 & -3 & -4 & 2 & -5 \\ 1 & -3 & -4 & 1 & -2 \\ -2 & 6 & 8 & -2 & 4 \end{array} \right]\nonumber\]
Supongamos que\(A\) es una\(m\times n\) matriz. Explique por qué el rango de no\(A\) es siempre mayor que\(\min \left( m,n\right) .\)
- Contestar
-
Es porque no se pueden tener más de filas distintas de\(\min \left( m,n\right)\) cero en la forma de fila-escalón reducido. Recordemos que el número de columnas pivotantes es el mismo que el número de filas distintas de cero a partir de la descripción de esta forma reducida de fila-escalón.
Indique si cada uno de los siguientes conjuntos de datos son posibles para la ecuación matricial\(AX=B\). Si es posible, describa el conjunto de soluciones. Es decir, decir si existe una solución única, ninguna solución o infinitamente muchas soluciones. Aquí,\(\left[ A |B \right]\) denota la matriz aumentada.
- \(A\)es una\(5\times 6\) matriz,\(rank\left( A\right) =4\) y\(rank\left[ A|B \right] =4.\)
- \(A\)es una\(3\times 4\) matriz,\(rank\left( A\right) =3\) y\(rank\left[ A|B\right] =2.\)
- \(A\)es una\(4\times 2\) matriz,\(rank\left( A\right) =4\) y\(rank\left[ A|B \right] =4.\)
- \(A\)es una\(5\times 5\) matriz,\(rank\left( A\right) =4\) y\(rank\left[ A|B \right] =5.\)
- \(A\)es una\(4\times 2\) matriz,\(rank\left( A\right) =2\) y\(rank\left[ A|B \right] =2\).
- Contestar
-
- Esto dice que\(B\) está en el lapso de cuatro de las columnas. Por lo tanto, las columnas no son independientes. Set de soluciones infinitas.
- Esto seguramente no puede suceder. Si agregas en otra columna, el rango no se hace menor.
- Esto dice que\(B\) está en el lapso de las columnas y las columnas deben ser independientes. No puedes tener el rango igual a 4 si solo tienes dos columnas.
- Esto dice que no\(B\) está en el lapso de las columnas. En este caso, no hay solución al sistema de ecuaciones representado por la matriz aumentada.
- En este caso, existe una solución única ya que las columnas de\(A\) son independientes.
Considera el sistema\(-5x+2y-z=0\) y\(-5x-2y-z=0.\) Ambas ecuaciones son iguales a cero y entonces\(-5x+2y-z=-5x-2y-z\) cual es equivalente a\(y=0.\) ¿Sigue eso\(x\) y\(z\) puede igualar a cualquier cosa? Observe que cuando\(x=1\),\(z=-4,\) y\(y=0\) están enchufados a las ecuaciones, las ecuaciones no son iguales\(0\). ¿Por qué?
- Contestar
-
Estas no son operaciones de fila legítimas. No conservan el conjunto de soluciones del sistema.
Equilibrar las siguientes reacciones químicas.
- \(KNO_{3}+H_{2}CO_{3}\rightarrow K_{2}CO_{3}+HNO_{3}\)
- \(AgI+Na_{2}S\rightarrow Ag_{2}S+NaI\)
- \(Ba_{3}N_{2}+H_{2}O\rightarrow Ba\left( OH\right) _{2}+NH_{3}\)
- \(CaCl_{2}+Na_{3}PO_{4}\rightarrow Ca_{3}\left( PO_{4}\right) _{2}+NaCl\)
En el apartado sobre variables adimensionales se observó que\(\rho V^{2}AB\) tiene las unidades de fuerza. Describir una manera sistemática de obtener tales combinaciones de las variables que produzcan algo que tenga las unidades de fuerza.
Considera el siguiente diagrama de cuatro circuitos.
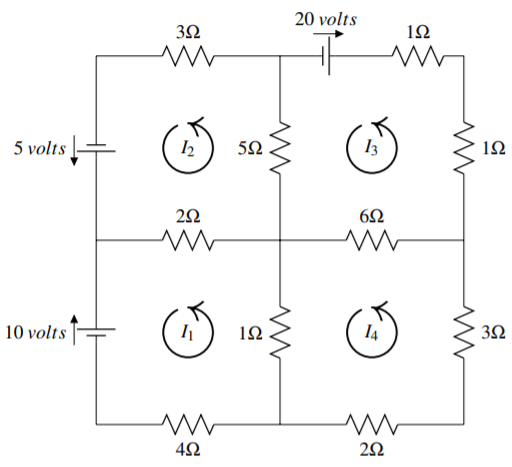
La corriente en amperios en los cuatro circuitos se denota por\(I_{1},I_{2},I_{3},I_{4}\) y se entiende que el movimiento es en sentido contrario a las agujas del reloj. Si\(I_{k}\) termina siendo negativo, entonces solo significa que la corriente fluye en el sentido de las agujas del reloj.
En el diagrama anterior, el circuito superior izquierdo debería dar la ecuación\[2I_{2}-2I_{1}+5I_{2}-5I_{3}+3I_{2}=5\nonumber \] Para el circuito de la parte inferior izquierda, deberías tener\[4I_{1}+I_{1}-I_{4}+2I_{1}-2I_{2}=-10\nonumber \] Escribir ecuaciones para cada uno de los otros dos circuitos y luego dar una solución al sistema de ecuaciones resultante.
- Contestar
-
Las otras dos ecuaciones son\[\begin{aligned} 6I_{3}-6I_{4}+I_{3}+I_{3}+5I_{3}-5I_{2} &=-20 \\ 2I_{4}+3I_{4}+6I_{4}-6I_{3}+I_{4}-I_{1} &=0\end{aligned}\] Entonces el sistema es\[\begin{array}{c} 2I_{2}-2I_{1}+5I_{2}-5I_{3}+3I_{2}=5 \\ 4I_{1}+I_{1}-I_{4}+2I_{1}-2I_{2}=-10 \\ 6I_{3}-6I_{4}+I_{3}+I_{3}+5I_{3}-5I_{2}=-20 \\ 2I_{4}+3I_{4}+6I_{4}-6I_{3}+I_{4}-I_{1}=0 \end{array}\nonumber \] La solución es:\[\begin{aligned} I_{1}&= -\frac{750}{373} \\ I_{2}&= -\frac{1421}{1119} \\ I_{3}&= -\frac{3061}{1119} \\ I_{4}&= -\frac{1718}{1119}\end{aligned}\]
Considera el siguiente diagrama de tres circuitos.
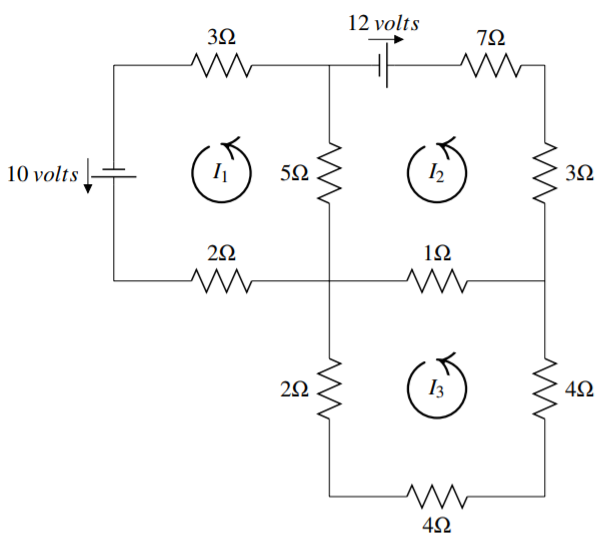
La corriente en amperios en los cuatro circuitos se denota por\(I_{1},I_{2},I_{3}\) y se entiende que el movimiento es en sentido contrario a las agujas del reloj. Si\(I_{k}\) termina siendo negativo, entonces solo significa que la corriente fluye en el sentido de las agujas del reloj.
Encuentra\(I_{1},I_{2},I_{3}\).
- Contestar
-
Tienes\[\begin{aligned} 2I_{1}+5I_{1}+3I_{1}-5I_{2} &= 10 \\ I_{2}- I_{3} +3I_{2}+7I_{2}+5I_{2}-5I_{1} &=-12 \\ 2I_{3}+4I_{3}+4I_{3}+I_{3}-I_{2} &= 0\end{aligned}\] Simplificando estos rendimientos\[\begin{aligned} 10I_{1}-5I_{2} &= 10 \\ -5I_{1} + 16I_{2}- I_{3} &=-12 \\ -I_{2} + 11I_{3} &=0\end{aligned}\] La solución viene dada por\[I_{1}=\frac{218}{295},I_{2}=-\frac{154}{295},I_{3}=-\frac{14}{295}\nonumber \]