4.3: Significado geométrico de la adición de vectores

Última actualización
Guardar como PDF

Page ID: 114515

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Entender la adición de vectores, geométricamente.

Recordemos que un elemento de\(\mathbb{R}^{n}\) es una lista ordenada de números. Para el caso específico de\(n=2,3\) esto se puede utilizar para determinar un punto en el espacio bidimensional o tridimensional. Este punto se especifica en relación con algunos ejes de coordenadas.

Considera el caso\(n=3\). Recordemos que tomar un vector y moverlo sin cambiar su longitud o dirección no cambia el vector. Esto es importante en la representación geométrica de la adición de vectores.

Supongamos que tenemos dos vectores,\(\vec{u}\) y\(\vec{v}\) en\(\mathbb{R}^{3}\). Cada uno de estos se puede dibujar geométricamente colocando la cola de cada vector en\(0\) y su punto en\(\left( u_{1}, u_{2}, u_{3}\right)\) y\(\left( v_{1}, v_{2}, v_{3}\right)\) respectivamente. Supongamos que deslizamos el vector\(\vec{v}\) para que su cola se asiente en el punto de\(\vec{u}\). Sabemos que esto no cambia el vector\(\vec{v}\). Ahora, dibuja un nuevo vector desde la cola de\(\vec{u}\) hasta el punto de\(\vec{v}\). Este vector es\(\vec{u}+\vec{v}\).

La significación geométrica de la adición de vectores en\(\mathbb{R}^n\) para cualquiera\(n\) se da en la siguiente definición.

Definición\(\PageIndex{1}\): Geometry of Vector Addition

Dejar\(\vec{u}\) y\(\vec{v}\) ser dos vectores. Deslízate\(\vec{v}\) para que la cola de\(\vec{v}\) esté en el punto de\(\vec{u}\). Después dibuja la flecha que va desde la cola de\(\vec{u}\) hasta el punto de\(\vec{v}\). Esta flecha representa el vector\(\vec{u}+\vec{v}\).

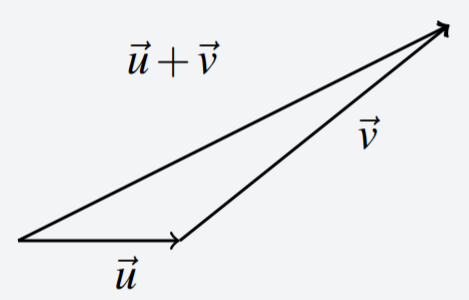
Esta definición se ilustra en la siguiente imagen en la que\(\vec{u}+\vec{v}\) se muestra para el caso especial\(n=3\).

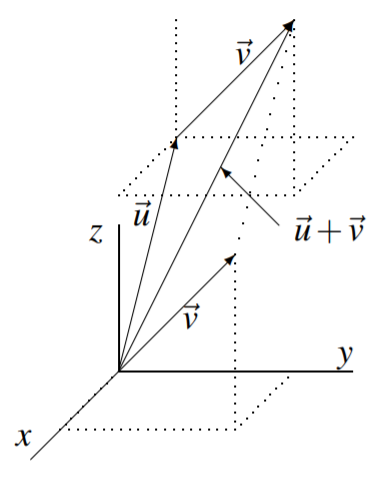
Observe el paralelogramo creado por\(\vec{u}\) y\(\vec{v}\) en el diagrama anterior. Entonces\(\vec{u} + \vec{v}\) es la diagonal dirigida del paralelogramo determinada por los dos vectores\(\vec{u}\) y\(\vec{v}\).

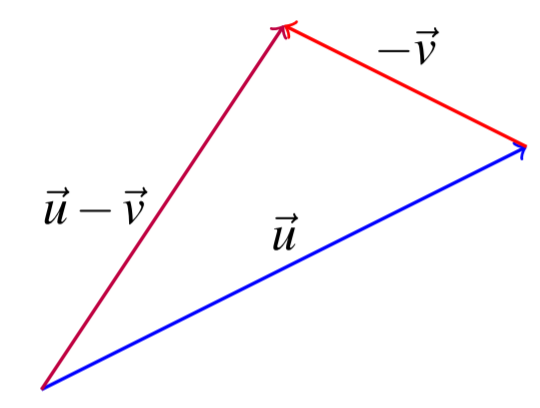
Cuando se tiene un vector\(\vec{v}\), su inversa aditiva\(-\vec{v}\) será el vector que tiene la misma magnitud\(\vec{v}\) pero la dirección opuesta. Cuando uno escribe\(\vec{u}-\vec{v,}\) el significado es\(\vec{u} + \left( -\vec{v}\right)\) como con los números reales. El siguiente ejemplo ilustra estas definiciones y convenciones.

Ejemplo\(\PageIndex{1}\): Graphing Vector Addition

Considere la siguiente imagen de vectores\(\vec{u}\) y\(\vec{v}\).

Esbozar una imagen de\(\vec{u}+\vec{v},\vec{u}-\vec{v}.\)

Solución

Primero haremos bosquejo\(\vec{u}+\vec{v}.\) Empezaremos por dibujar\(\vec{u}\) y luego en el punto de\(\vec{u}\), colocaremos la cola de\(\vec{v}\) como se muestra. Entonces\(\vec{u}+\vec{v}\) es el vector que resulta de dibujar un vector desde la cola de\(\vec{u}\) hasta la punta de\(\vec{v}\).

Siguiente considerar\(\vec{u}-\vec{v}.\) Esto significa A\(\vec{u}+\left( -\vec{v} \right) .\) partir de la descripción geométrica anterior de la adición de vectores,\(-\vec{v}\) es el vector que tiene la misma longitud pero que apunta en la dirección opuesta a\(\vec{v}\). Aquí hay una foto.