4.4: Longitud de un Vector
- Page ID
- 114561
- Encuentra la longitud de un vector y la distancia entre dos puntos en\(\mathbb{R}^n\).
- Encuentra el vector de unidad correspondiente a un vector en\(\mathbb{R}^n\).
En esta sección, exploramos lo que se entiende por la longitud de un vector en\(\mathbb{R}^n\). Desarrollamos este concepto mirando primero la distancia entre dos puntos en\(\mathbb{R}^n\).
Primero, consideraremos el concepto de distancia para\(\mathbb{R}\), es decir, para puntos adentro\(\mathbb{R}^1\). Aquí, la distancia entre dos puntos\(P\) y\(Q\) viene dada por el valor absoluto de su diferencia. Denotamos la distancia entre\(P\) y\(Q\) por la\(d(P,Q)\) cual se define como\[d(P,Q) = \sqrt{ \left( P-Q\right) ^{2}} \label{distance1}\]
Consideremos ahora el caso para\(n=2\), demostrado por el siguiente cuadro.
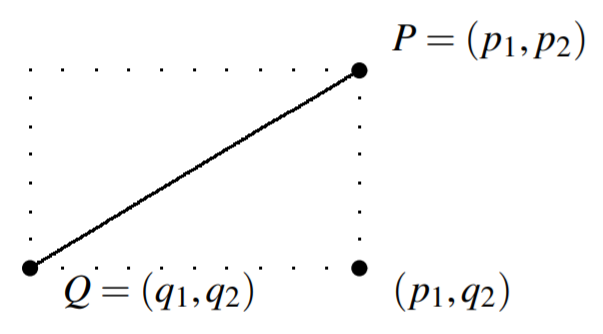
Hay dos puntos\(P =\left( p_{1},p_{2}\right)\) y\(Q = \left(q_{1},q_{2}\right)\) en el plano. La distancia entre estos puntos se muestra en la imagen como una línea continua. Observe que esta línea es la hipotenusa de un triángulo rectángulo que es la mitad del rectángulo que se muestra en líneas punteadas. Queremos encontrar la longitud de esta hipotenusa que dará la distancia entre los dos puntos. Obsérvese que las longitudes de los lados de este triángulo son\(\left| p_{1}-q_{1}\right|\) y\(\left| p_{2}-q_{2}\right|\), el valor absoluto de la diferencia en estos valores. Por lo tanto, el Teorema de Pitágoras implica que la longitud de la hipotenusa (y por lo tanto la distancia entre\(P\) y\(Q\)) es igual\[\left( \left| p_{1}-q_{1}\right| ^{2}+\left| p_{2}-q_{2}\right| ^{2}\right) ^{1/2}=\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2} \label{distance2}\]
Ahora supongamos\(n=3\) y vamos\(P = \left( p_{1},p_{2},p_{3}\right)\) y\(Q = \left( q_{1},q_{2},q_{3}\right)\) sean dos puntos en\(\mathbb{R}^{3}.\) Considera la siguiente imagen en la que la línea sólida une los dos puntos y una línea punteada une los puntos\(\left( q_{1},q_{2},q_{3}\right)\) y\(\left( p_{1},p_{2},q_{3}\right) .\)
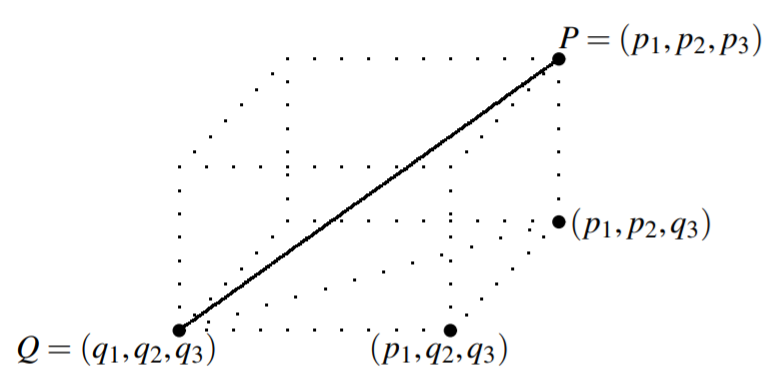
Aquí, necesitamos usar el Teorema de Pitágoras dos veces para encontrar la longitud de la línea sólida. Primero, por el Teorema de Pitágoras, la longitud de la línea punteada que une\(\left( q_{1},q_{2},q_{3}\right)\) e\(\left( p_{1},p_{2},q_{3}\right)\) iguala\[\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2}\nonumber \] mientras que la longitud de la línea que se une\(\left( p_{1},p_{2},q_{3}\right)\) a\(\left( p_{1},p_{2},p_{3}\right)\) es justo\(\left| p_{3}-q_{3}\right| .\) Por lo tanto, por el Teorema de Pitágoras nuevamente, la longitud de la línea que une los puntos\(P = \left( p_{1},p_{2},p_{3}\right)\) y \(Q = \left( q_{1},q_{2},q_{3}\right)\)es igual\[\left( \left( \left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}\right) ^{1/2}\right) ^{2}+\left( p_{3}-q_{3}\right) ^{2}\right) ^{1/2}\nonumber \]\[=\left( \left( p_{1}-q_{1}\right) ^{2}+\left( p_{2}-q_{2}\right) ^{2}+\left( p_{3}-q_{3}\right) ^{2}\right) ^{1/2} \label{distance3}\]
Esta discusión motiva la siguiente definición para la distancia entre puntos en\(\mathbb{R}^n\).
Dejar\(P=\left( p_{1},\cdots ,p_{n}\right)\) y\(Q=\left( q_{1},\cdots ,q_{n}\right)\) ser dos puntos adentro\(\mathbb{R}^{n}\). Entonces la distancia entre estos puntos se define como\[\text{ distance between }P\text{ and } Q\text{ } = d( P, Q ) = \left( \sum_{k=1}^{n}\left\vert p_{k}-q_{k}\right\vert ^{2}\right) ^{1/2}\nonumber \] Esto se llama la fórmula de distancia. También podemos escribir\(\left\vert P - Q \right\vert\) como la distancia entre\(P\) y\(Q\).
De la discusión anterior, se puede ver que Definición\(\PageIndex{1}\) sostiene para los casos especiales\(n=1,2,3\), como en Ecuaciones\(\eqref{distance1}\),\(\eqref{distance2}\),\(\eqref{distance3}\). En el siguiente ejemplo, usamos Definición\(\PageIndex{1}\) para encontrar la distancia entre dos puntos en\(\mathbb{R}^4\).
Encuentra la distancia entre los puntos\(P\) y\(Q\) en\(\mathbb{R}^{4}\), donde\(P\) y\(Q\) están dadas por\[P=\left( 1,2,-4,6\right)\nonumber \] y\[Q=\left( 2,3,-1,0\right)\nonumber \]
Solución
Usaremos la fórmula dada en Definición \(\PageIndex{1}\)para encontrar la distancia entre\(P\) y\(Q\). Usa la fórmula de distancia y escribe\[d(P,Q)= \left( \left( 1-2\right) ^{2}+\left( 2-3\right) ^{2}+\left( -4-\left( -1\right) \right) ^{2}+\left( 6-0\right)^{2}\right) ^{\frac{1}{2}} = 47\nonumber \]
Por lo tanto,\(d( P,Q) = \sqrt{47}.\)
Existen ciertas propiedades de la distancia entre puntos que son importantes en nuestro estudio. Estos se describen en el siguiente teorema.
Dejar\(P\) y\(Q\) ser puntos adentro\(\mathbb{R}^n\), y dejar que la distancia entre ellos,\(d( P, Q)\), se dé como en Definición\(\PageIndex{1}\). Entonces, se mantienen las siguientes propiedades.
- \(d( P, Q) = d( Q, P)\)
- \(d( P, Q) \geq 0\), y es igual a 0 exactamente cuando\(P = Q.\)
Existen muchas aplicaciones del concepto de distancia. Por ejemplo, dados dos puntos, podemos preguntar qué colección de puntos son todos la misma distancia entre los puntos dados. Esto se explora en el siguiente ejemplo.
Describir los puntos en los\(\mathbb{R}^3\) que se encuentran a la misma distancia entre\(\left( 1,2,3\right)\) y\(\left( 0,1,2\right) .\)
Solución
Que\(P = \left( p_1 , p_2, p_3\right)\) sea tal punto. Por lo tanto,\(P\) es la misma distancia de\(\left( 1,2,3\right)\) y\(\left( 0,1,2\right) .\) Entonces por Definición \(\PageIndex{1}\),\[\sqrt{\left( p_1 -1\right) ^{2}+\left( p_2 -2\right) ^{2}+\left( p_3-3\right) ^{2}}= \sqrt{\left( p_1 - 0 \right)^{2}+\left( p_2-1\right) ^{2}+\left( p_3-2\right) ^{2}}\nonumber \] Cuadrando ambos lados obtenemos\[\left( p_1 -1\right) ^{2}+\left( p_2 -2\right) ^{2}+\left( p_3 -3\right) ^{2}=p_1^{2}+\left( p_2-1\right) ^{2}+\left( p_3 -2\right) ^{2}\nonumber \] y así\[ \ p_1^{2}-2p_1+14+p_2^{2}-4p_2+p_3^{2}-6p_3=p_1^{2}+p_2^{2}-2p_2+5+p_3^{2}-4p_3\nonumber \] Simplificando, esto se convierte en lo\[-2p_1+14-4p_2-6p_3=-2p_2+5-4p_3\nonumber \] que se puede escribir como\[2p_1+2p_2+2p_3=-9 \label{distanceplane}\] Por lo tanto, los puntos \(P = \left( p_1,p_2,p_3\right)\)que están a la misma distancia de cada uno de los puntos dados forman un plano cuya ecuación viene dada por\(\eqref{distanceplane}\).
Ahora podemos usar nuestra comprensión de la distancia entre dos puntos para definir lo que se entiende por la longitud de un vector. Considera la siguiente definición.
Dejar\(\vec{u} = \left[ u_{1} \cdots u_{n} \right]^T\) ser un vector en\(\mathbb{R}^n\). Entonces, la longitud de\(\vec{u}\), escrito\(\| \vec{u} \|\) viene dada por\[\| \vec{u} \| = \sqrt{ u_{1}^2 + \cdots + u_{n}^2}\nonumber \]
Esta definición corresponde a Definición\(\PageIndex{1}\), si se considera que el vector\(\vec{u}\) tiene su cola en el punto\(0 = \left( 0, \cdots ,0 \right)\) y su punta en el punto\(U = \left(u_1, \cdots, u_n \right)\). Entonces la longitud de\(\vec{u}\) es igual a la distancia entre\(0\) y\(U\),\(d(0,U)\). En general,\(d(P,Q)=||\vec{PQ}||\).
Considera Ejemplo \(\PageIndex{1}\). Por Definición \(\PageIndex{2}\), también podríamos encontrar la distancia entre\(P\) y\(Q\) como la longitud del vector que los conecta. De ahí que si tuviéramos que dibujar un vector\(\overrightarrow{PQ}\) con su cola en\(P\) y su punto en\(Q\), este vector tendría longitud igual a\(\sqrt{47}\).
Concluimos esta sección con una nueva definición para el caso especial de vectores de longitud\(1\).
Dejar\(\vec{u}\) ser un vector en\(\mathbb{R}^{n}\). Entonces, llamamos a\(\vec{u}\) un vector unitario si tiene longitud 1, es decir, si\[\| \vec{u} \| = 1\nonumber \]
Dejar\(\vec{v}\) ser un vector en\(\mathbb{R}^{n}\). Entonces, el vector\(\vec{u}\) que tiene la misma dirección que\(\vec{v}\) pero longitud igual a\(1\) es el vector unitario correspondiente de\(\vec{v}\). Este vector viene dado por\[\vec{u} = \frac{1}{\| \vec{v} \|} \vec{v}\nonumber \]
A menudo usamos el término normalizar para referirnos a este proceso. Cuando normalizamos un vector, encontramos el vector unitario correspondiente de longitud\(1\). Considera el siguiente ejemplo.
Dejar\(\vec{v}\) ser dado por\[\vec{v} = \left[ \begin{array}{rrr} 1 & -3 & 4 \end{array} \right]^T\nonumber \] Encuentra el vector de unidad\(\vec{u}\) que tiene la misma dirección que\(\vec{v}\).
Solución
Usaremos Definición\(\PageIndex{3}\) para resolver esto. Por lo tanto, necesitamos encontrar la longitud de la\(\vec{v}\) cual, por Definición\(\PageIndex{2}\) se da por\[\| \vec{v} \| = \sqrt{ v_{1}^2 + v_{2}^2+ v_{3}^2}\nonumber \] Usando los valores correspondientes encontramos que\[\begin{aligned} \| \vec{v} \| &= \sqrt{ 1^2 + \left(-3 \right)^2 + 4^2} \\ &= \sqrt{ 1 + 9 + 16} \\ &= \sqrt{26} \end{aligned}\] Para encontrar\(\vec{u}\), dividimos\(\vec{v}\) por\(\sqrt{26}\). El resultado es\[\begin{aligned} \vec{u} &= \frac{1}{\| \vec{v} \|} \vec{v} \\ &= \frac{1}{\sqrt{26}} \left[ \begin{array}{rrr} 1 & -3 & 4 \end{array} \right]^T \\ &= \left[ \begin{array}{rrr} \frac{1}{\sqrt{26}} & -\frac{3}{\sqrt{26}} & \frac{4}{\sqrt{26}} \end{array} \right]^T\end{aligned}\]
Puedes verificar usando la Definición\(\PageIndex{1}\) que\(\| \vec{u} \| = 1\).


