4.6: Líneas paramétricas
- Page ID
- 114507
- Encuentra el vector y las ecuaciones paramétricas de una línea.
Podemos utilizar el concepto de vectores y puntos para encontrar ecuaciones para líneas arbitrarias en\(\mathbb{R}^n\), aunque en esta sección el foco estará en las líneas en\(\mathbb{R}^3\).
Para comenzar, considere el caso\(n=1\) así que tenemos\(\mathbb{R}^{1}=\mathbb{R}\). Aquí sólo hay una línea que es la línea numérica familiar, que es\(\mathbb{R}\) en sí misma. Por lo tanto, no es necesario explorar el caso de\(n=1\) más.
Ahora consideremos el caso donde\(n=2\), en otras palabras\(\mathbb{R}^2\). Dejar\(P\) y\(P_0\) ser dos puntos diferentes en los\(\mathbb{R}^{2}\) que están contenidos en una línea\(L\). Dejar\(\vec{p}\) y\(\vec{p_0}\) ser los vectores de posición para los puntos\(P\) y\(P_0\) respectivamente. Supongamos que\(Q\) es un punto arbitrario sobre\(L\). Considera el siguiente diagrama.
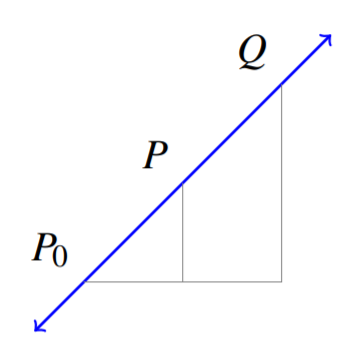
Nuestro objetivo es poder definir\(Q\) en términos de\(P\) y\(P_0\). Considere el vector\(\overrightarrow{P_0P} = \vec{p} - \vec{p_0}\) que tiene su cola en\(P_0\) y punto en\(P\). Si agregamos\(\vec{p} - \vec{p_0}\) al vector de posición\(\vec{p_0}\) para\(P_0\), la suma sería un vector con su punto en\(P\). En otras palabras,\[\vec{p} = \vec{p_0} + (\vec{p} - \vec{p_0})\nonumber \]
Ahora supongamos que íbamos\(t(\vec{p} - \vec{p_0})\) a agregar a\(\vec{p}\) donde\(t\) hay algún escalar. Se puede ver que al hacerlo, podríamos encontrar un vector con su punto en\(Q\). En otras palabras, podemos encontrar\(t\) tal que\[\vec{q} = \vec{p_0} + t \left( \vec{p}- \vec{p_0}\right)\nonumber \]
Esta ecuación determina la línea\(L\) en\(\mathbb{R}^2\). De hecho, determina una línea\(L\) en\(\mathbb{R}^n\). Considera la siguiente definición.
Supongamos que una línea\(L\) en\(\mathbb{R}^{n}\) contiene los dos puntos diferentes\(P\) y\(P_0\). Dejar\(\vec{p}\) y\(\vec{p_0}\) ser los vectores de posición de estos dos puntos, respectivamente. Entonces,\(L\) es la colección de puntos\(Q\) que tienen el vector de posición\(\vec{q}\) dado por\[\vec{q}=\vec{p_0}+t\left( \vec{p}-\vec{p_0}\right)\nonumber \] donde\(t\in \mathbb{R}\).
Vamos\(\vec{d} = \vec{p} - \vec{p_0}\). Entonces\(\vec{d}\) es el vector de dirección para\(L\) y la ecuación vectorial para\(L\) viene dada por\[\vec{p}=\vec{p_0}+t\vec{d}, t\in\mathbb{R}\nonumber \]
Obsérvese que esta definición concuerda con la noción habitual de una línea en dos dimensiones y por lo que esta es congruente con conceptos anteriores. Considerar ahora puntos en\(\mathbb{R}^3\). Si un punto\(P \in \mathbb{R}^3\) viene dado por\(P = \left( x,y,z \right)\),\(P_0 \in \mathbb{R}^3\) por\(P_0 = \left( x_0, y_0, z_0 \right)\), entonces podemos escribir\[\left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{c} x_0 \\ y_0 \\ z_0 \end{array} \right] + t \left[ \begin{array}{c} a \\ b \\ c \end{array} \right] \nonumber \] donde\(\vec{d} = \left[ \begin{array}{c} a \\ b \\ c \end{array} \right]\). Esta es la ecuación vectorial de\(L\) escrito en forma de componente.
El siguiente teorema afirma que tal ecuación es de hecho una línea.
Déjalo\(\vec{a},\vec{b}\in \mathbb{R}^{n}\) con\(\vec{b}\neq \vec{0}\). Entonces\(\vec{x}=\vec{a}+t\vec{b},\; t\in \mathbb{R}\), es una línea.
- Prueba
-
Vamos\(\vec{x_{1}}, \vec{x_{2}} \in \mathbb{R}^n\). Definir\(\vec{x_{1}}=\vec{a}\) y dejar\(\vec{x_{2}}-\vec{x_{1}}=\vec{b}\). Ya que\(\vec{b} \neq \vec{0}\), se deduce que\(\vec{x_{2}}\neq \vec{x_{1}}.\) Entonces\(\vec{a}+t\vec{b}=\vec{x_{1}} + t\left( \vec{x_{2}}-\vec{x_{1}}\right)\). De ello se deduce que\(\vec{x}=\vec{a}+t\vec{b}\) es una línea que contiene los dos puntos diferentes\(X_1\) y\(X_2\) cuyos vectores de posición están dados por\(\vec{x}_1\) y\(\vec{x}_2\) respectivamente.
Podemos usar la discusión anterior para encontrar la ecuación de una línea cuando se le dan dos puntos distintos. Considera el siguiente ejemplo.
Encuentra una ecuación vectorial para la línea a través de los puntos\(P_0 = \left( 1,2,0\right)\) y\(P = \left( 2,-4,6\right).\)
Solución
Usaremos la definición de una línea dada anteriormente en Definición \(\PageIndex{1}\)para escribir esta línea en la forma
\[\vec{q}=\vec{p_0}+t\left( \vec{p}-\vec{p_0}\right)\nonumber \]
Vamos\(\vec{q} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B\). Entonces, podemos encontrar\(\vec{p}\) y\(\vec{p_0}\) tomando los vectores de posición de puntos\(P\) y\(P_0\) respectivamente. Entonces,
\[\vec{q}=\vec{p_0}+t\left( \vec{p}-\vec{p_0}\right)\nonumber \]se puede escribir como
\[\left[ \begin{array}{c} x \\ y \\ z \\ \end{array} \right]B = \left[ \begin{array}{c} 1 \\ 2 \\ 0 \end{array} \right]B + t \left[ \begin{array}{r} 1 \\ -6 \\ 6 \end{array} \right]B, \;t\in \mathbb{R}\nonumber \]
Aquí, el vector de dirección\(\left[ \begin{array}{r} 1 \\ -6 \\ 6 \end{array} \right]B\) se obtiene por\(\vec{p} - \vec{p_0} = \left[ \begin{array}{r} 2 \\ -4 \\ 6 \end{array} \right]B - \left[ \begin{array}{r} 1 \\ 2 \\ 0 \end{array} \right]B\) como se indicó anteriormente en Definición\(\PageIndex{1}\).
Observe que en el ejemplo anterior dijimos que encontramos “una” ecuación vectorial para la línea, no “la” ecuación. La razón de esta terminología es que hay infinitamente muchas ecuaciones vectoriales diferentes para una misma línea. Para ver esto, reemplace\(t\) por otro parámetro, digamos\(3s.\) Luego se obtiene una ecuación vectorial diferente para la misma línea porque se obtiene el mismo conjunto de puntos.
En Ejemplo\(\PageIndex{1}\), el vector dado por\(\left[ \begin{array}{r} 1 \\ -6 \\ 6 \end{array} \right]B\) es el vector de dirección definido en Definición\(\PageIndex{1}\). Si conocemos el vector de dirección de una línea, así como un punto en la línea, podemos encontrar la ecuación vectorial.
Considera el siguiente ejemplo.
Encontrar una ecuación vectorial para la línea que contiene el punto\(P_0 = \left( 1,2,0\right)\) y tiene vector de dirección\(\vec{d} = \left[ \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right]B\)
Solución
Usaremos Definición\(\PageIndex{1}\) para escribir esta línea en el formulario\(\vec{p}=\vec{p_0}+t\vec{d},\; t\in \mathbb{R}\). Se nos da el vector de dirección\(\vec{d}\). Para encontrar\(\vec{p_0}\), podemos usar el vector de posición del punto\(P_0\). Esto viene dado por\(\left[ \begin{array}{c} 1 \\ 2 \\ 0 \end{array} \right]B.\) Dejar\(\vec{p} = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B\), la ecuación para la línea viene dada por\[\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B = \left[ \begin{array}{c} 1 \\ 2 \\ 0 \end{array} \right]B + t \left[ \begin{array}{c} 1 \\ 2 \\ 1 \end{array} \right]B, \;t\in \mathbb{R} \label{vectoreqn}\]
A veces elegimos escribir una línea como la que se da\(\eqref{vectoreqn}\) en la forma\[\begin{array}{ll} \left. \begin{array}{l} x=1+t \\ y=2+2t \\ z=t \end{array} \right\} & \mbox{where} \; t\in \mathbb{R} \end{array} \label{parameqn}\] Este conjunto de ecuaciones dan la misma información que\(\eqref{vectoreqn}\), y se llama la ecuación paramétrica de la línea.
Considera la siguiente definición.
Dejar\(L\) ser una línea en la\(\mathbb{R}^3\) que tiene vector de dirección\(\vec{d} = \left[ \begin{array}{c} a \\ b \\ c \end{array} \right]B\) y pasa por el punto\(P_0 = \left( x_0, y_0, z_0 \right)\). Entonces, dejando\(t\) ser un parámetro, podemos escribir\(L\) como\[\begin{array}{ll} \left. \begin{array}{c} x = x_0 + ta \\ y = y_0 + tb \\ z = z_0 + tc \end{array} \right\} & \mbox{where} \; t\in \mathbb{R} \end{array}\nonumber \] Esto se llama una ecuación paramétrica de la línea\(L\).
Se puede verificar que la forma discutida a continuación Ejemplo\(\PageIndex{2}\) en ecuación\(\eqref{parameqn}\) es de la forma dada en Definición\(\PageIndex{2}\).
Hay otra forma para una línea que es útil, que es la forma simétrica. Considera la línea dada por\(\eqref{parameqn}\). Se puede resolver para que el parámetro\(t\) escriba\[\begin{array}{l} t=x-1 \\ t=\frac{y-2}{2} \\ t=z \end{array}\nonumber \] Por lo tanto,\[x-1=\frac{y-2}{2}=z\nonumber \] Esta es la forma simétrica de la línea.
En el siguiente ejemplo, observamos cómo tomar la ecuación de una línea de forma simétrica a forma paramétrica.
Supongamos que la forma simétrica de una línea es\[\frac{x-2}{3}=\frac{y-1}{2}=z+3\nonumber \] Escribir la línea en forma paramétrica así como en forma vectorial.
Solución
Queremos escribir esta línea en la forma que nos da Definición\(\PageIndex{2}\). Esto es de la forma\[\begin{array}{ll} \left. \begin{array}{c} x = x_0 + ta \\ y = y_0 + tb \\ z = z_0 + tc \end{array} \right\} & \mbox{where} \; t\in \mathbb{R} \end{array}\nonumber \]
Dejar\(t=\frac{x-2}{3},t=\frac{y-1}{2}\) y\(t=z+3\), como se da en la forma simétrica de la línea. Luego resolviendo\(x,y,z,\) rendimientos\[\begin{array}{ll} \left. \begin{array}{c} x=2 + 3t \\ y=1 + 2t \\ z=-3 + t \end{array} \right\} & \mbox{with} \;t\in \mathbb{R} \end{array}\nonumber \]
Esta es la ecuación paramétrica para esta línea.
Ahora, queremos escribir esta línea en la forma que nos da Definición\(\PageIndex{1}\). Esta es la forma\[\vec{p}=\vec{p_0}+t\vec{d}\nonumber\] donde\(t\in \mathbb{R}\). Esta ecuación se convierte\[\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]B = \left[ \begin{array}{r} 2 \\ 1 \\ -3 \end{array} \right]B + t \left[ \begin{array}{r} 3 \\ 2 \\ 1 \end{array} \right]B, \;t\in \mathbb{R}\nonumber \]


