4.7: El producto Dot

Resultados

1. Calcular el producto punto de vectores, y utilizar esto para calcular proyecciones vectoriales.

El producto Dot

Hay dos formas de multiplicar vectores que son de gran importancia en las aplicaciones. El primero de ellos se llama el producto punto. Cuando tomamos el punto producto de vectores, el resultado es un escalar. Por esta razón, el producto punto también se llama el producto escalar y en ocasiones el producto interno. La definición es la siguiente.

Definición\(\PageIndex{1}\): Dot Product

\(\vec{u},\vec{v}\)Dejen ser dos vectores en\(\mathbb{R}^{n}\). Luego definimos el producto punto\(\vec{u}\bullet \vec{v}\) como\[\vec{u}\bullet \vec{v} = \sum_{k=1}^{n}u_{k}v_{k}\nonumber \]

El producto punto a veces\(\vec{u}\bullet \vec{v}\) se denota como\((\vec{u},\vec{v})\) donde reemplaza una coma\(\bullet\). También se puede escribir como\(\left\langle \vec{u},\vec{v}\right\rangle\). Si escribimos los vectores como matrices de columna o fila, es igual al producto de la matriz\(\vec{v}\vec{w}^{T}\).

Considera el siguiente ejemplo.

Ejemplo\(\PageIndex{1}\): Compute a Dot Product

Buscar\(\vec{u} \bullet \vec{v}\) para\[\vec{u} = \left[ \begin{array}{r} 1 \\ 2 \\ 0 \\ -1 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 0 \\ 1 \\ 2 \\ 3 \end{array} \right]\nonumber \]

Solución

Por Definición\(\PageIndex{1}\), debemos computar\[\vec{u}\bullet \vec{v} = \sum_{k=1}^{4}u_{k}v_{k}\nonumber \]

Esto viene dado por\[\begin{aligned} \vec{u} \bullet \vec{v} &= (1)(0) + (2)(1) + (0)(2) + (-1)(3) \\ &= 0 + 2 + 0 + -3 \\ &= -1\end{aligned}\]

Con esta definición, hay varias propiedades importantes satisfechas por el producto dot.

Proposición\(\PageIndex{1}\): Properties of the Dot Product

Dejar\(k\) y\(p\) denotar escalares y\(\vec{u},\vec{v},\vec{w}\) denotar vectores. Entonces el producto dot\(\vec{u} \bullet \vec{v}\) satisface las siguientes propiedades.

• \(\vec{u}\bullet \vec{v}= \vec{v}\bullet \vec{u}\)
• \(\vec{u}\bullet \vec{u}\geq 0 \text{ and equals zero if and only if }\vec{u}=\vec{0}\)
• \(\left( k\vec{u}+p\vec{v}\right) \bullet \vec{w}=k\left( \vec{u}\bullet \vec{w}\right) +p\left( \vec{v}\bullet \vec{w}\right)\)
• \(\vec{u}\bullet\left( k\vec{v}+p\vec{w}\right) =k\left( \vec{u}\bullet \vec{v}\right) +p\left( \vec{u}\bullet \vec{w}\right)\)
• \(\| \vec{u}\| ^{2}=\vec{u}\bullet \vec{u}\)

Prueba

La prueba se deja como ejercicio.

Esta proposición nos dice que también podemos usar el producto punto para encontrar la longitud de un vector.

Ejemplo\(\PageIndex{2}\): Length of a Vector

Encuentra la longitud de Es\[\vec{u} = \left[ \begin{array}{r} 2 \\ 1 \\ 4 \\ 2 \end{array} \right]\nonumber \] decir, encuentra\(\| \vec{u} \| .\)

Solución

Por Proposición\(\PageIndex{1}\),\(\| \vec{u} \| ^{2} = \vec{u} \bullet \vec{u}\). Por lo tanto,\(\| \vec{u} \| = \sqrt {\vec{u} \bullet \vec{u}}\). Primero, computar\(\vec{u} \bullet \vec{u}\).

Esto viene dado por\[\begin{aligned} \vec{u} \bullet \vec{u} &= (2)(2) + (1)(1) + (4)(4) + (2)(2) \\ &= 4 + 1 + 16 + 4 \\ &= 25\end{aligned}\]

Entonces,\[\begin{aligned} \| \vec{u} \| &= \sqrt {\vec{u} \bullet \vec{u}} \\ &= \sqrt{25} \\ &= 5\end{aligned}\]

Tal vez desee comparar esto con nuestra definición anterior de longitud, dada en la Definición 4.4.2.

La desigualdad de Cauchy Schwarz es una desigualdad fundamental satisfecha por el producto punto. Se da en el siguiente teorema.

Teorema\(\PageIndex{1}\): Cauchy Schwarz Inequality

El producto punto satisface la desigualdad\[\left\vert \vec{u}\bullet \vec{v}\right\vert \leq \| \vec{u}\| \| \vec{v}\| \label{cauchy}\] Además se obtiene la igualdad si y solo si uno de\(\vec{u}\) o\(\vec{v}\) es un múltiplo escalar del otro.

Prueba

Primero señalar que si\(\vec{v}=\vec{0}\) ambos lados de\(\eqref{cauchy}\) igual cero y así la desigualdad se mantiene en este caso. Por lo tanto, se asumirá en lo que sigue a eso\(\vec{v}\neq \vec{0}\).

Definir una función de\(t\in \mathbb{R}\) por\[f\left( t\right) =\left( \vec{u}+t\vec{v}\right) \bullet \left( \vec{u}+ t\vec{v}\right)\nonumber \] Entonces por Proposición\(\PageIndex{1}\),\(f\left( t\right) \geq 0\) para todos\(t\in \mathbb{R}\). También de Proposición\(\PageIndex{1}\)\[\begin{aligned} f\left( t\right) &=\vec{u}\bullet \left( \vec{u}+t\vec{v}\right) + t\vec{v}\bullet \left( \vec{u}+t\vec{v}\right) \\ &=\vec{u}\bullet \vec{u}+t\left( \vec{u}\bullet \vec{v}\right) + t \vec{v}\bullet \vec{u}+ t^{2}\vec{v}\bullet \vec{v} \\ &=\| \vec{u}\| ^{2}+2t\left( \vec{u}\bullet \vec{v}\right) +\| \vec{v}\| ^{2}t^{2}\end{aligned}\]

Ahora bien, esto significa que la gráfica de\(y=f\left( t\right)\) es una parábola que se abre y o bien su vértice toca el\(t\) eje o bien toda la gráfica está por encima del\(t\) eje. En el primer caso, existe algún\(t\) lugar\(f\left( t\right) =0\) y esto requiere\(\vec{u}+t\vec{v}=\vec{0}\) por lo que un vector es un múltiplo del otro. Entonces claramente se sostiene la igualdad\(\eqref{cauchy}\). En el caso donde no\(\vec{v}\) es un múltiplo de\(\vec{u}\), se sigue\(f\left( t\right) >0\) para todo lo\(t\) que dice no\(f\left( t\right)\) tiene ceros reales y así a partir de la fórmula cuadrática,\[\left( 2\left( \vec{u}\bullet \vec{v}\right) \right) ^{2}-4\| \vec{u} \| ^{2}\| \vec{v}\| ^{2}<0\nonumber \] que es equivalente a\(\left\vert \vec{u}\bullet \vec{v} \right\vert <\| \vec{u}\| \| \vec{v}\|\).

Observe que esta prueba se basó únicamente en las propiedades del producto punto listado en la Proposición\(\PageIndex{1}\). Esto significa que cada vez que una operación satisface estas propiedades, se mantiene la desigualdad de Cauchy Schwarz. Hay muchas otras instancias de estas propiedades además de los vectores en\(\mathbb{R}^{n}\).

La desigualdad de Cauchy Schwarz proporciona otra prueba de la desigualdad triangular para las distancias en\(\mathbb{R}^{n}\).

Teorema\(\PageIndex{2}\): Triangle Inequality

For\(\vec{u},\vec{v}\in \mathbb{R}^{n}\)\[\| \vec{u}+\vec{v}\| \leq \| \vec{u}\| +\| \vec{v} \| \label{triangleineq1}\] y la igualdad se mantiene si y solo si uno de los vectores es un múltiplo escalar no negativo del otro.

También\[\| \| \vec{u}\| -\| \vec{v}\| \| \leq \| \vec{u}-\vec{v}\| \label{triangleineq2}\]

Prueba

Por propiedades del producto punto y la desigualdad Cauchy Schwarz,\[\begin{aligned} \| \vec{u}+\vec{v}\| ^{2} &= \left( \vec{u}+\vec{v}\right) \bullet \left( \vec{u}+\vec{v}\right) \\ & =\left( \vec{u}\bullet \vec{u}\right) +\left( \vec{u}\bullet \vec{v}\right) +\left(\vec{v}\bullet \vec{u}\right) +\left( \vec{v}\bullet \vec{v}\right) \\ &=\| \vec{u}\| ^{2}+2\left( \vec{u}\bullet \vec{v}\right)+\| \vec{v}\| ^{2} \\ &\leq \| \vec{u}\| ^{2}+2\left\vert \vec{u}\bullet \vec{v}\right\vert +\| \vec{v}\| ^{2} \\ &\leq \| \vec{u}\| ^{2}+2\| \vec{u}\| \| \vec{v}\| +\| \vec{v}\| ^{2} =\left( \| \vec{u}\| +\| \vec{v}\|\right) ^{2}\end{aligned}\] De ahí,\[\| \vec{u}+\vec{v}\| ^{2} \leq \left( \| \vec{u}\| +\| \vec{v}\| \right) ^{2}\nonumber \] Tomando raíces cuadradas de ambos lados se obtiene\(\eqref{triangleineq1}\).

Queda por considerar cuándo ocurre la igualdad. Supongamos\(\vec{u} = \vec{0}\). Entonces,\(\vec{u} = 0 \vec{v}\) y se verifica la afirmación sobre cuándo ocurre la igualdad. El mismo argumento sostiene si\(\vec{v} = \vec{0}\). Por lo tanto, se puede suponer que ambos vectores son distintos de cero. Para obtener la igualdad en lo\(\eqref{triangleineq1}\) anterior, Teorema\(\PageIndex{1}\) implica que uno de los vectores debe ser un múltiplo del otro. Diga\(\vec{v}= k \vec{u}\). Si\(k <0\) entonces la igualdad no puede darse en\(\eqref{triangleineq1}\) porque en este caso\[\vec{u}\bullet \vec{v} =k \| \vec{u}\| ^{2}<0<\left| k \right| \| \vec{u}\| ^{2}=\left| \vec{u}\bullet \vec{v}\right|\nonumber \] Por lo tanto,\(k \geq 0.\)

Para obtener la otra forma del triángulo la desigualdad escribe\[\vec{u}=\vec{u}-\vec{v}+\vec{v}\nonumber \] así\[\begin{aligned} \| \vec{u}\| & =\| \vec{u}-\vec{v}+\vec{v}\| \\ & \leq \| \vec{u}-\vec{v}\| +\| \vec{v}\| \end{aligned}\] Por lo tanto,\[\| \vec{u}\| -\| \vec{v}\| \leq \| \vec{u}-\vec{v} \| \label{triangleineq3}\] Del mismo modo,\[\| \vec{v}\| -\| \vec{u}\| \leq \| \vec{v}-\vec{u} \| =\| \vec{u}-\vec{v}\| \label{triangleineq4}\] se deduce de\(\eqref{triangleineq3}\) y\(\eqref{triangleineq4}\) eso\(\eqref{triangleineq2}\) sostiene. Esto se debe\(\left| \| \vec{u}\| -\| \vec{v}\| \right|\) a que es igual al lado izquierdo de cualquiera\(\eqref{triangleineq3}\) o\(\eqref{triangleineq4}\) y de cualquier manera,\(\left| \| \vec{u}\| -\| \vec{v}\| \right| \leq \| \vec{u}-\vec{v}\|\).

La significación geométrica del producto de punto

Dados dos vectores,\(\vec{u}\) y\(\vec{v}\), el ángulo incluido es el ángulo entre estos dos vectores el cual viene dado por\(\theta\) tal que\(0 \leq \theta \leq \pi\). El producto de punto se puede utilizar para determinar el ángulo incluido entre dos vectores. Considera la siguiente imagen donde\(\theta\) da el ángulo incluido.

Figura\(\PageIndex{1}\)

Proposición\(\PageIndex{2}\): The Dot Product and the Included Angle

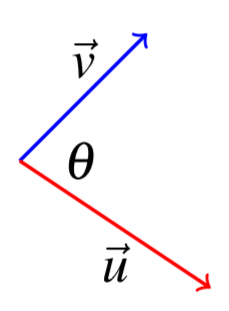
Dejar\(\vec{u}\) y\(\vec{v}\) ser dos vectores adentro\(\mathbb{R}^n\), y dejar\(\theta\) ser el ángulo incluido. Entonces se mantiene la siguiente ecuación. \[\vec{u}\bullet \vec{v}=\| \vec{u}\| \| \vec{v} \| \cos \theta\nonumber \]

En palabras, el producto punto de dos vectores es igual al producto de la magnitud (o longitud) de los dos vectores multiplicado por el coseno del ángulo incluido. Tenga en cuenta que esto da una descripción geométrica del producto punto que no depende explícitamente de las coordenadas de los vectores.

Considera el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\): Find the Angle Between Two Vectors

Encuentra el ángulo entre los vectores dados por\[\vec{u} = \left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ 4 \\ 1 \end{array} \right]\nonumber \]

Solución

Por Proposición\(\PageIndex{2}\),\[\vec{u}\bullet \vec{v}=\| \vec{u}\| \| \vec{v} \| \cos \theta\nonumber \] Por lo tanto,\[\cos \theta =\frac{\vec{u}\bullet \vec{v}}{\| \vec{u}\| \| \vec{v} \|}\nonumber \]

Primero, podemos calcular\(\vec{u}\bullet \vec{v}\). Por definición\(\PageIndex{1}\), esto equivale\[\vec{u}\bullet \vec{v} = (2)(3) + (1)(4)+(-1)(1) = 9\nonumber \]

Entonces,\[\begin{array}{c} \| \vec{u} \| = \sqrt{(2)(2)+(1)(1)+(1)(1)}=\sqrt{6}\\ \| \vec{v} \| = \sqrt{(3)(3)+(4)(4)+(1)(1)}=\sqrt{26} \end{array}\nonumber \] Por lo tanto, el coseno del ángulo incluido es igual\[\cos \theta =\frac{9}{\sqrt{26}\sqrt{6}}=0.7205766...\nonumber \]

Con el coseno conocido, el ángulo se puede determinar calculando el coseno inverso de ese ángulo, dando aproximadamente\(\theta =0.76616\) radianes.

Otra aplicación de la descripción geométrica del producto punto es encontrar el ángulo entre dos líneas. Normalmente se asumiría que las líneas se cruzan. En algunas situaciones, sin embargo, puede tener sentido hacer esta pregunta cuando las líneas no se cruzan, como el ángulo entre dos trayectorias de objetos. En cualquier caso entendemos que significa el ángulo más pequeño entre (cualquiera de) sus vectores de dirección. La única sutileza aquí es que si\(\vec{u}\) es un vector de dirección para una línea, entonces también lo es cualquier múltiplo\(k\vec{u}\), y así encontraremos ángulos complementarios entre todos los ángulos entre vectores de dirección para dos líneas, y simplemente tomamos la más pequeña de las dos.

Ejemplo\(\PageIndex{4}\): Find the Angle Between Two Lines

Encuentra el ángulo entre las dos líneas\[L_1: \; \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} 1 \\ 2 \\ 0 \end{array} \right] +t\left[ \begin{array}{r} -1 \\ 1 \\ 2 \end{array} \right]\nonumber \] y\[L_2: \; \left[ \begin{array}{r} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{r} 0 \\ 4 \\ -3 \end{array} \right] +s\left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right]\nonumber \]

Solución

Se puede verificar que estas líneas no se cruzan, pero como se discutió anteriormente esto no importa y simplemente encontramos el ángulo más pequeño entre cualquier vector de direcciones para estas líneas.

Para ello, primero encontramos el ángulo entre los vectores de dirección dados anteriormente:\[\vec{u}=\left[ \begin{array}{r} -1 \\ 1 \\ 2 \end{array} \right],\; \vec{v}=\left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right]\nonumber \]

Para encontrar el ángulo, resolvemos la siguiente ecuación\(\theta\)\[\vec{u}\bullet \vec{v}=\| \vec{u}\| \| \vec{v} \| \cos \theta\nonumber \] para obtener\(\cos \theta = -\frac{1}{2}\) y ya que elegimos ángulos incluidos entre\(0\) y\(\pi\) obtenemos\(\theta = \frac{2 \pi}{3}\).

Ahora los ángulos entre dos vectores de dirección cualesquiera para estas líneas serán\(\frac{2 \pi}{3}\) o su complemento\(\phi = \pi - \frac{2 \pi}{3} = \frac{\pi}{3}\). Elegimos el ángulo más pequeño, y por lo tanto concluimos que el ángulo entre las dos líneas es\(\frac{\pi}{3}\).

También podemos usar Proposición\(\PageIndex{2}\) para calcular el producto punto de dos vectores.

Ejemplo\(\PageIndex{5}\): Using Geometric Description to Find a Dot Product

Dejar\(\vec{u},\vec{v}\) ser vectores con\(\| \vec{u} \| = 3\) y\(\| \vec{v} \| = 4\). Supongamos que el ángulo entre\(\vec{u}\) y\(\vec{v}\) es\(\pi / 3\). Encuentra\(\vec{u}\bullet \vec{v}\).

Solución

A partir de la descripción geométrica del producto punto en Proposición\(\PageIndex{2}\)\[\vec{u}\bullet \vec{v}=(3)(4) \cos \left( \pi / 3\right) =3\times 4\times 1/2=6\nonumber \]

Se dice que dos vectores distintos de cero son perpendiculares, a veces también llamados ortogonales, si el ángulo incluido es\(\pi /2\) radianes (\(90^{\circ }).\)

Considera la siguiente proposición.

Proposición\(\PageIndex{3}\): Perpendicular Vectors

Dejar\(\vec{u}\) y\(\vec{v}\) ser vectores distintos de cero en\(\mathbb{R}^n\). Entonces,\(\vec{u}\) y\(\vec{v}\) se dice que son perpendiculares exactamente cuando\[\vec{u} \bullet \vec{v} = 0\nonumber \]

Prueba

Esto se desprende directamente de la Proposición\(\PageIndex{2}\). Primero si el producto punto de dos vectores distintos de cero es igual a\(0\), esto nos dice que\(\cos \theta =0\) (aquí es donde necesitamos vectores distintos de cero). Así\(\theta = \pi /2\) y los vectores son perpendiculares.

Si por otro lado\(\vec{v}\) es perpendicular a\(\vec{u}\), entonces el ángulo incluido son\(\pi /2\) radianes. De ahí\(\cos \theta =0\) y\(\vec{u} \bullet \vec{v} = 0\).

Considera el siguiente ejemplo.

Ejemplo\(\PageIndex{6}\): Determine if Two Vectors are Perpendicular

Determinar si los dos vectores,\[\vec{u}= \left[ \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 1 \\ 3 \\ 5 \end{array} \right]\nonumber \] son perpendiculares.

Solución

Para determinar si estos dos vectores son perpendiculares, calculamos el producto punto. Esto viene dado por\[\vec{u} \bullet \vec{v} = (2)(1) + (1)(3) + (-1)(5) = 0\nonumber \] Por lo tanto, por Proposición\(\PageIndex{3}\) estos dos vectores son perpendiculares.

Proyecciones

En algunas aplicaciones, deseamos escribir un vector como una suma de dos vectores relacionados. A través del concepto de proyecciones, podemos encontrar estos dos vectores. Primero, exploramos un teorema importante. El resultado de este teorema aportará nuestra definición de proyección vectorial.

Teorema\(\PageIndex{3}\): Vector Projections

Dejar\(\vec{v}\) y\(\vec{u}\) ser vectores distintos de cero. Entonces existen vectores únicos\(\vec{v}_{||}\) y\(\vec{v}_{\bot }\) tales que\[\vec{v}=\vec{v}_{||}+\vec{v}_{\bot } \label{projection}\] donde\(\vec{v}_{||}\) es un múltiplo escalar de\(\vec{u}\), y\(\vec{v}_{\bot}\) es perpendicular a\(\vec{u}\).

Prueba

Supongamos que\(\eqref{projection}\) sostiene y\(\vec{v}_{||}= k \vec{u}\). Tomando el producto punteado de ambos lados de\(\eqref{projection}\) con\(\vec{u}\) y usando\(\vec{v}_{\bot }\bullet \vec{u}=0,\) esto rinde lo\[\begin{array}{ll} \vec{v}\bullet \vec{u} & = ( \vec{v}_{||}+\vec{v}_{\bot }) \bullet \vec{u} \\ & = k\vec{u} \bullet \vec{u} + \vec{v}_{\bot} \bullet \vec{u} \\ & = k \| \vec{u}\| ^{2} \end{array}\nonumber \] que requiere\(k =\vec{v}\bullet \vec{u} / \| \vec{u}\| ^{2}.\) Así no puede haber más de un vector\(\vec{v}_{||}\). Se deduce\(\vec{v}_{\bot }\) debe igualar\(\vec{v}-\vec{v}_{||}.\) Esto verifica que no pueda haber más de una opción para ambos\(\vec{v}_{||}\) y\(\vec{v}_{\bot }\) y demuestra su singularidad.

Ahora vamos\[\vec{v}_{||} = \frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\vec{u}\nonumber \] y vamos\[\vec{v}_{\bot }=\vec{v}-\vec{v}_{||}=\vec{v}-\frac{\vec{v}\bullet \vec{u}} {\| \vec{u}\| ^{2}}\vec{u}\nonumber \] Entonces\(\vec{v}_{||}= k\vec{u}\) dónde\(k =\frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\). Sólo queda por verificar\(\vec{v}_{\bot }\bullet \vec{u}=0.\) Pero\[\begin{aligned} \vec{v}_{\bot }\bullet \vec{u} &= \vec{v}\bullet \vec{u}-\frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\vec{u}\bullet \vec{u} \\ &= \vec{v}\bullet\vec{u}-\vec{v}\bullet \vec{u}\\ &= 0 \end{aligned}\]

El vector\(\vec{v}_{||}\) en Teorema\(\PageIndex{3}\) se llama la proyección de\(\vec{v}\) sobre\(\vec{u}\) y se denota por\[\vec{v}_{||} = \mathrm{proj}_{\vec{u}}\left( \vec{v}\right)\nonumber \]

Ahora hacemos una definición formal de la proyección vectorial.

Definición\(\PageIndex{2}\): Vector Projection

Dejar\(\vec{u}\) y\(\vec{v}\) ser vectores. Entonces, la proyección de\(\vec{v}\) onto\(\vec{u}\) viene dada por\[\mathrm{proj}_{\vec{u}}\left( \vec{v}\right) =\left( \frac{\vec{v}\bullet \vec{u}}{\vec{u}\bullet \vec{u}}\right) \vec{u} = \frac{\vec{v}\bullet \vec{u}}{\| \vec{u}\| ^{2}}\vec{u}\nonumber \]

Considera el siguiente ejemplo de una proyección.

Ejemplo\(\PageIndex{7}\): Find the Projection of One Vector Onto Another

Encuentra\(\mathrm{proj}_{\vec{u}}\left( \vec{v}\right)\) si\[\vec{u}= \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right], \vec{v}= \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right]\nonumber \]

Solución

Podemos usar la fórmula proporcionada en Definición\(\PageIndex{2}\) para encontrar\(\mathrm{proj}_{\vec{u}}\left( \vec{v}\right)\). Primero, computar\(\vec{v} \bullet \vec{u}\). Esto viene dado por\[\begin{aligned} \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right] \bullet \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] &= (2)(1) + (3)(-2) + (-4)(1) \\ &= 2 - 6 - 4 \\ &= -8\end{aligned}\] Similarmente,\(\vec{u} \bullet \vec{u}\) viene dado por\[\begin{aligned} \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] \bullet \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] &= (2)(2) + (3)(3) + (-4)(-4) \\ &= 4 + 9 + 16 \\ &= 29\end{aligned}\]

Por lo tanto, la proyección es igual a\[\begin{aligned} \mathrm{proj}_{\vec{u}}\left( \vec{v}\right) &=-\frac{8}{29} \left[ \begin{array}{r} 2 \\ 3 \\ -4 \end{array} \right] \\ &= \left[ \begin{array}{r} - \frac{16}{29} \\ - \frac{24}{29} \\ \frac{32}{29} \end{array} \right]\end{aligned}\]

Concluiremos esta sección con una importante aplicación de proyecciones. Supongamos que\(P\) se les da una línea\(L\) y un punto tal que no\(P\) esté contenido en\(L\). Mediante el uso de proyecciones, podemos determinar la distancia más corta de\(P\) a\(L\).

Ejemplo\(\PageIndex{8}\): Shortest Distance from a Point to a Line

Dejar\(P = (1,3,5)\) ser un punto adentro\(\mathbb{R}^3\), y dejar\(L\) ser la línea que pasa por el punto\(P_0 = (0,4,-2)\) con vector de dirección\(\vec{d} = \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right]\). Encuentra la distancia más corta desde\(P\) la línea\(L\), y encuentra el punto\(Q\) en el\(L\) que está más cerca\(P\).

Solución

Para determinar la distancia más corta de\(P\) a\(L\), primero encontraremos el vector\(\overrightarrow{P_0P}\) y luego encontraremos la proyección de este vector sobre\(L\). El vector\(\overrightarrow{P_0P}\) viene dado por\[\left[ \begin{array}{r} 1 \\ 3 \\ 5 \end{array} \right] - \left[ \begin{array}{r} 0 \\ 4 \\ -2 \end{array} \right] = \left[ \begin{array}{r} 1 \\ -1 \\ 7 \end{array} \right]\nonumber \]

Entonces, si\(Q\) es el punto\(L\) más cercano a\(P\), se deduce que\[\begin{aligned} \overrightarrow{P_0Q} &= \mathrm{proj}_{\vec{d}}\overrightarrow{P_0P} \\ &= \left( \frac{ \overrightarrow{P_0P}\bullet \vec{d}}{\|\vec{d}\|^2}\right) \vec{d} \\ &= \frac{15}{9} \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right] \\ &= \frac{5}{3} \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right]\end{aligned}\]

Ahora, la distancia de\(P\) a\(L\) viene dada por\[\| \overrightarrow{QP} \| = \| \overrightarrow{P_0P} - \overrightarrow{P_0Q}\| = \sqrt{26}\nonumber \]

El punto\(Q\) se encuentra sumando el vector\(\overrightarrow{P_0Q}\) al vector de posición\(\overrightarrow{0P_0}\) para\(P_0\) lo siguiente\[\begin{aligned} \left[ \begin{array}{r} 0 \\ 4 \\ -2 \end{array} \right] + \frac{5}{3} \left[ \begin{array}{r} 2 \\ 1 \\ 2 \end{array} \right] &= \left[ \begin{array}{r} \frac{10}{3} \\ \frac{17}{3} \\ \frac{4}{3} \end{array} \right]\end{aligned}\]

Por lo tanto,\(Q = (\frac{10}{3}, \frac{17}{3}, \frac{4}{3})\).