7.3: Aplicaciones de la Teoría Espectral

Resultados

1. Utilice la diagonalización para encontrar una alta potencia de una matriz.
2. Utilice la diagonalización para resolver sistemas dinámicos.

Elevación de una matriz a una alta potencia

Supongamos que tenemos una matriz\(A\) y queremos encontrar\(A^{50}\). Uno podría intentar multiplicarse\(A\) consigo mismo 50 veces, pero esto es computacionalmente extremadamente intensivo (¡pruébalo!). Sin embargo, la diagonalización nos permite calcular altas potencias de una matriz con relativa facilidad. Supongamos que\(A\) es diagonalizable, así que eso\(P^{-1}AP=D\). Podemos reorganizar esta ecuación para escribir\(A=PDP^{-1}\).

Ahora, considere\(A^{2}\). Ya que\(A=PDP^{-1}\), de ello se deduce que\[A^{2} = \left( PDP^{-1}\right) ^{2}=PDP^{-1}PDP^{-1}=PD^{2}P^{-1}\nonumber\]

Del mismo modo,\[A^3 = \left( PDP^{-1}\right) ^{3}=PDP^{-1}PDP^{-1}PDP^{-1}=PD^{3}P^{-1}\nonumber\]

En general,\[A^n = \left( PDP^{-1}\right) ^{n}=PD^{n}P^{-1}\nonumber\]

Por lo tanto, hemos reducido el problema a encontrar\(D^{n}\). Para poder computar\(D^{n}\), entonces porque\(D\) es diagonal solo necesitamos elevar cada entrada en la diagonal principal de\(D\) a la potencia de\(n\).

A través de este método, podemos calcular grandes potencias de matrices. Considera el siguiente ejemplo.

Ejemplo\(\PageIndex{1}\): Raising a Matrix to a High Power

Let\(A=\left [ \begin{array}{rrr} 2 & 1 & 0 \\ 0 & 1 & 0 \\ -1 & -1 & 1 \end{array} \right ].\) Find\(A^{50}.\)

Solución

Primero diagonalizaremos\(A\). Los pasos se dejan como ejercicio y es posible que desee verificar que los valores propios de\(A\) son\(\lambda_1 =1, \lambda_2=1\), y\(\lambda_3=2\).

Los vectores propios básicos correspondientes a\(\lambda_1, \lambda_2 = 1\) son\[X_1 = \left [ \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right ] , X_2 = \left [ \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \right ]\nonumber\]

El autovector básico correspondiente a\(\lambda_3 = 2\) es\[X_3 = \left [ \begin{array}{r} -1 \\ 0 \\ 1 \end{array} \right ]\nonumber\]

Ahora construimos\(P\) usando los vectores propios básicos de\(A\) como las columnas de\(P\). Así\[P= \left [ \begin{array}{rrr} X_1 & X_2 & X_3 \end{array} \right ] = \left [ \begin{array}{rrr} 0 & -1 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right ]\nonumber\] Entonces también\[P^{-1}=\left [ \begin{array}{rrr} 1 & 1 & 1 \\ 0 & 1 & 0 \\ -1 & -1 & 0 \end{array} \right ]\nonumber\] que tal vez quieras verificar.

Entonces,\[\begin{aligned} P^{-1}AP &=\left [ \begin{array}{rrr} 1 & 1 & 1 \\ 0 & 1 & 0 \\ -1 & -1 & 0 \end{array} \right ] \left [ \begin{array}{rrr} 2 & 1 & 0 \\ 0 & 1 & 0 \\ -1 & -1 & 1 \end{array} \right ] \left [ \begin{array}{rrr} 0 & -1 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right ] \\ &=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right ] \\ &= D\end{aligned}\]

Ahora se sigue reordenando la ecuación que\[A=PDP^{-1}=\left [ \begin{array}{rrr} 0 & -1 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right ] \left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right ] \left [ \begin{array}{rrr} 1 & 1 & 1 \\ 0 & 1 & 0 \\ -1 & -1 & 0 \end{array} \right ]\nonumber\]

Por lo tanto,\[\begin{aligned} A^{50} &=PD^{50}P^{-1} \\ &=\left [ \begin{array}{rrr} 0 & -1 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right ] \left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right ] ^{50}\left [ \begin{array}{rrr} 1 & 1 & 1 \\ 0 & 1 & 0 \\ -1 & -1 & 0 \end{array} \right ] \end{aligned}\]

Por nuestra discusión anterior,\(D^{50}\) se encuentra de la siguiente manera. \[\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right ] ^{50}=\left [ \begin{array}{rrr} 1^{50} & 0 & 0 \\ 0 & 1^{50} & 0 \\ 0 & 0 & 2^{50} \end{array} \right ]\nonumber\]

De ello se deduce que\[\begin{aligned} A^{50} &=\left [ \begin{array}{rrr} 0 & -1 & -1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right ] \left [ \begin{array}{rrr} 1^{50} & 0 & 0 \\ 0 & 1^{50} & 0 \\ 0 & 0 & 2^{50} \end{array} \right ] \left [ \begin{array}{rrr} 1 & 1 & 1 \\ 0 & 1 & 0 \\ -1 & -1 & 0 \end{array} \right ] \\ &=\left [ \begin{array}{ccc} 2^{50} & -1+2^{50} & 0 \\ 0 & 1 & 0 \\ 1-2^{50} & 1-2^{50} & 1 \end{array} \right ] \end{aligned}\]

A través de la diagonalización, podemos calcular eficientemente una alta potencia de\(A\). Sin esto, ¡nos veríamos obligados a multiplicar esto a mano!

En la siguiente sección se explora otra interesante aplicación de la diagonalización.

Elevación de una matriz simétrica a una alta potencia

Ya hemos visto cómo usar la diagonalización matricial para computar potencias de matrices. Esto requiere calcular los valores propios de la matriz\(A\), y encontrar una matriz invertible de vectores propios\(P\) tal que\(P^{-1}AP\) sea diagonal. En esta sección veremos que si la matriz\(A\) es simétrica (ver Definición 2.5.2), entonces en realidad podemos encontrar tal matriz\(P\) que es una matriz ortogonal de vectores propios. Así\(P^{-1}\) es simplemente su transposición\(P^T\), y\(P^TAP\) es diagonal. Cuando esto sucede decimos que\(A\) es ortogonalmente diagonalizable

De hecho esto sucede si y sólo si\(A\) es una matriz simétrica como se muestra en el siguiente teorema importante.

Teorema\(\PageIndex{1}\): Principal Axis Theorem

Las siguientes condiciones son equivalentes para una\(n \times n\) matriz\(A\):

1. \(A\)es simétrico.
2. \(A\)tiene un conjunto ortonormal de vectores propios.
3. \(A\)es ortogonalmente diagonalizable.

Prueba

La prueba completa está más allá de este curso, pero para dar una idea supongamos que\(A\) tiene un conjunto ortonormal de vectores propios, y dejar\(P\) consistir en estos vectores propios como columnas. Entonces\(P^{-1}=P^T\), y\(P^TAP=D\) una matriz diagonal. Pero entonces\(A=PDP^T\), y\[A^T=(PDP^T)^T = (P^T)^TD^TP^T=PDP^T=A\nonumber\] así\(A\) es simétrico.

Ahora dada una matriz simétrica\(A\), se muestra que los vectores propios correspondientes a diferentes valores propios son siempre ortogonales. Por lo que basta aplicar el proceso Gram-Schmidt sobre el conjunto de vectores propios básicos de cada autovalor para obtener un conjunto ortonormal de vectores propios.

Esto lo demostramos en el siguiente ejemplo.

Ejemplo\(\PageIndex{2}\): Orthogonal Diagonalization of a Symmetric Matrix

Vamos\(A=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{3}{2} \end{array} \right ] .\) Encuentra una matriz ortogonal\(P\) tal que\(P^{T}AP\) sea una matriz diagonal.

Solución

En este caso, verificar que los valores propios son 2 y 1. Primero encontraremos un vector propio para el valor propio\(2\). Esto implica reducir la fila de la siguiente matriz aumentada. \[\left [ \begin{array}{ccc|c} 2 - 1 & 0 & 0 & 0 \\ 0 & 2- \frac{3}{2} & - \frac{1}{2} & 0 \\ 0 & - \frac{1}{2} & 2- \frac{3}{2} & 0 \end{array} \right ]\nonumber\]La forma reducida de fila-escalón es\[\left [ \begin{array}{rrr|r} 1 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right ]\nonumber\] y así un autovector es\[\left [ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right ]\nonumber\] Finalmente para obtener un autovector de longitud uno (unidad de vector propio) simplemente dividimos este vector por su longitud para producir:\[\left [ \begin{array}{c} 0 \\ \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right ]\nonumber\]

A continuación considere el caso del valor propio\(1\). Para obtener vectores propios básicos, la matriz que necesita ser reducida de fila en este caso es\[\left [ \begin{array}{ccc|c} 1-1 & 0 & 0 & 0 \\ 0 & 1- \frac{3}{2} & - \frac{1}{2} & 0 \\ 0 & - \frac{1}{2} & 1- \frac{3}{2} & 0 \end{array} \right ]\nonumber\] La forma de escalón de fila reducida es\[\left [ \begin{array}{rrr|r} 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right ]\nonumber\] Por lo tanto, los vectores propios son de la forma\[\left [ \begin{array}{c} s \\ -t \\ t \end{array} \right ]\nonumber\] Tenga en cuenta que todos estos vectores son automáticamente ortogonales a vectores propios correspondientes al primer valor propio. Esto se desprende del hecho de que\(A\) es simétrico, como se mencionó anteriormente.

Obtenemos vectores propios básicos\[\left [ \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \right ] \text{ and }\left [ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right ]\nonumber\] Ya que ellos mismos son ortogonales (por suerte aquí) no necesitamos usar el proceso Gram-Schmidt y en su lugar simplemente normalizar estos vectores para obtener\[\left [ \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \right ] \text{ and }\left [ \begin{array}{c} 0 \\ -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right ]\nonumber\] Una matriz ortogonal\(P\) para diagonalizar ortogonalmente\(A\) se obtiene luego dejando que estos vectores básicos sean las columnas. \[P= \left [ \begin{array}{ccc} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right ]\nonumber\]Verificamos que esto funcione. \(P^{T}AP\)es de la forma\[\left [ \begin{array}{ccc} 0 & - \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right ] \left [ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{3}{2} \end{array} \right ] \left [ \begin{array}{ccc} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right ]\nonumber\]\[= \left [ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right ]\nonumber\] que es la matriz diagonal deseada.

Ahora podemos aplicar esta técnica para calcular eficientemente altas potencias de una matriz simétrica.

Ejemplo\(\PageIndex{3}\): Powers of a Symmetric Matrix

Vamos a\(A=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{3}{2} \end{array} \right ] .\) Calcular\(A^7\).

Solución

Encontramos en Ejemplo\(\PageIndex{2}\) que\(P^TAP=D\) es diagonal, donde

\[P= \left [ \begin{array}{ccc} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right ] \text{ and } D = \left [ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right ]\nonumber \]

Así\(A=PDP^T\) y\(A^7=PDP^T \; PDP^T \; \cdots PDP^T = PD^7P^T\) que da:

\[\begin{array}{rr} A^7 & = \left [ \begin{array}{ccc} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right ] \left [ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right ] ^7 \left [ \begin{array}{ccc} 0 & - \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right ] \\ & = \left [ \begin{array}{ccc} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right ] \left [ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2^7 \end{array} \right ] \left [ \begin{array}{ccc} 0 & - \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right ] \\ & = \left [ \begin{array}{ccc} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right ] \left [ \begin{array}{ccc} 0 & - \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ 1 & 0 & 0 \\ 0 & \frac{2^7}{\sqrt{2}} & \frac{2^7}{\sqrt{2}} \end{array} \right ] \\ & = \left [ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \frac{2^7+1}{2} & \frac{2^7-1}{2}\\ 0 & \frac{2^7-1}{2} & \frac{2^7+1}{2} \end{array} \right ] \\ \end{array}\nonumber\]

Matrices de Markov

Existen aplicaciones de gran importancia las cuales cuentan con un tipo especial de matriz. Las matrices cuyas columnas constan de números no negativos que suman a uno se llaman matrices de Markov. Una aplicación importante de las matrices de Markov es en la migración poblacional, como se ilustra en la siguiente definición.

Definición\(\PageIndex{1}\): Migration Matrices

Dejar que\(m\) las ubicaciones sean denotadas por los números\(1,2,\cdots ,m.\) Supongamos que es el caso que cada año la proporción de residentes en ubicación\(j\) que se mueven a ubicación\(i\) es\(a_{ij}\). También supongamos que nadie escapa o emigra de sin estas\(m\) ubicaciones. Esta última suposición requiere\(\sum_{i}a_{ij}=1\), y significa que la matriz\(A\), tal que\(A = \left [ a_{ij} \right ]\), es una matriz de Markov. En este contexto, también\(A\) se denomina matriz migratoria.

Consideremos el siguiente ejemplo que demuestra esta situación.

Ejemplo\(\PageIndex{4}\): Migration Matrix

Dejar\(A\) ser una matriz de Markov dada por\[A = \left [ \begin{array}{rr} .4 & .2 \\ .6 & .8 \end{array} \right ]\nonumber\] Verify que\(A\) es una matriz de Markov y describir las entradas de\(A\) en términos de migración poblacional.

Solución

Las columnas de\(A\) están compuestas por números no negativos que suman a\(1\). De ahí,\(A\) es una matriz de Markov.

Ahora, considere las entradas\(a_{ij}\) de\(A\) en términos de población. El ingreso\(a_{11} = .4\) es la proporción de residentes en la ubicación uno que permanecen en el lugar uno en un período de tiempo determinado. La entrada\(a_{21} = .6\) es la proporción de residentes en la ubicación 1 que se trasladan a la ubicación 2 en el mismo periodo de tiempo. La entrada\(a_{12} = .2\) es la proporción de residentes en la ubicación 2 que se trasladan a la ubicación 1. Finalmente, la entrada\(a_{22} = .8\) es la proporción de residentes en la ubicación 2 que permanecen en la ubicación 2 en este periodo de tiempo.

Considerada como una matriz de Markov, estos números suelen identificarse con probabilidades. De ahí que podamos decir que la probabilidad de que un residente de ubicación uno se quede en la ubicación uno en el periodo de tiempo es\(.4\).

Observe que en Ejemplo\(\PageIndex{4}\) si inicialmente había decir 15 mil personas en la ubicación 1 y 10 miles en la ubicación 2, entonces después de un año habría\(.4 \times 15 + .2 \times 10 = 8\) miles de personas en la ubicación 1 al año siguiente, y de igual manera habría\(.6 \times 15 + .8 \times 10 = 17\) miles de personas en la ubicación 2 el año siguiente.

Más generalmente deja\(X_n=\left [ x_{1n} \cdots x_{mn}\right ] ^{T}\) donde\(x_{in}\) está la población de ubicación\(i\) en periodo de tiempo\(n\). Llamamos\(X_n\) al vector de estado en periodo\(n\). En particular, llamamos\(X_0\) al vector de estado inicial. Dejando\(A\) ser la matriz de migración, calculamos la población en cada ubicación\(i\) un periodo de tiempo después por\(AX_n\). Con el fin de encontrar la población de ubicación\(i\) después de\(k\) años, calculamos el\(i^{th}\) componente de\(A^{k}X.\) Esta discusión se resume en el siguiente teorema.

Teorema\(\PageIndex{2}\): State Vector

Dejar\(A\) ser la matriz migratoria de una población y dejar\(X_n\) ser el vector cuyas entradas dan a la población de cada ubicación en periodo de tiempo\(n\). Entonces\(X_n\) es el vector de estado en periodo\(n\) y de ello se deduce que\[X_{n+1} = A X_n\nonumber\]

La suma de las entradas de\(X_n\) será igual a la suma de las entradas del vector inicial\(X_{0}\). Desde las columnas de\(A\) suma a\(1\), esta suma se conserva para cada multiplicación por\(A\) como se demuestra a continuación. \[\sum_{i}\sum_{j}a_{ij}x_{j}=\sum_{j}x_{j}\left( \sum_{i}a_{ij}\right) =\sum_{j}x_{j}\nonumber\]

Considera el siguiente ejemplo.

Ejemplo\(\PageIndex{5}\): Using a Migration Matrix

Considere la matriz de migración\[A = \left [ \begin{array}{rrr} .6 & 0 & .1 \\ .2 & .8 & 0 \\ .2 & .2 & .9 \end{array} \right ]\nonumber\] para las ubicaciones\(1,2,\) y\(3.\) Supongamos que inicialmente hay\(100\) residentes en ubicación\(1\),\(200\) en ubicación\(2\) y\(400\) en ubicación\(3\). Encuentra la población en las tres localidades posteriores\(1,2,\) y\(10\) unidades de tiempo.

Solución

Usando el Teorema\(\PageIndex{2}\) podemos encontrar la población en cada ubicación usando la ecuación\(X_{n+1} = AX_n\). Para la población tras\(1\) unidad, calculamos de la\(X_1 = AX_0\) siguiente manera. \[\begin{aligned} X_1 &= AX_0 \\ \left [ \begin{array}{r} x_{11} \\ x_{21} \\ x_{31} \end{array}\right ] &= \left [ \begin{array}{rrr} .6 & 0 & .1 \\ .2 & .8 & 0 \\ .2 & .2 & .9 \end{array} \right ] \left [ \begin{array}{r} 100 \\ 200 \\ 400 \end{array} \right ] \\ &= \left [ \begin{array}{r} 100 \\ 180 \\ 420 \end{array}\right ]\end{aligned}\]Por lo tanto, después de un período de tiempo, la ubicación\(1\) tiene\(100\) residentes, la ubicación\(2\) tiene\(180\) y la ubicación\(3\) tiene\(420\). Observe que la población total se encuentra sin cambios, simplemente migra dentro de las ubicaciones dadas. Encontramos las ubicaciones después de dos periodos de tiempo de la misma manera. \[\begin{aligned} X_2 &= AX_1 \\ \left [ \begin{array}{r} x_{12} \\ x_{22} \\ x_{32} \end{array}\right ] &= \left [ \begin{array}{rrr} .6 & 0 & .1 \\ .2 & .8 & 0 \\ .2 & .2 & .9 \end{array} \right ] \left [ \begin{array}{r} 100 \\ 180 \\ 420 \end{array} \right ] \\ &= \left [ \begin{array}{r} 102 \\ 164 \\ 434 \end{array}\right ]\end{aligned}\]

Podríamos avanzar de esta manera para encontrar las poblaciones después de periodos de\(10\) tiempo. Sin embargo a partir de nuestra discusión anterior, podemos simplemente calcular\(\left( A^{n}X_0\right) _{i}\), donde\(n\) denota el número de periodos de tiempo que han pasado. Por lo tanto, calculamos las poblaciones en cada ubicación después de\(10\) unidades de tiempo de la siguiente manera. \[\begin{aligned} X_{10} &= A^{10}X_0 \\ \left [ \begin{array}{r} x_{1 10} \\ x_{2 10} \\ x_{3 10} \end{array} \right ] &= \left [ \begin{array}{rrr} .6 & 0 & .1 \\ .2 & .8 & 0 \\ .2 & .2 & .9 \end{array} \right ] ^{10}\left [ \begin{array}{r} 100 \\ 200 \\ 400 \end{array} \right ] \\ &= \left [ \begin{array}{c} 115.\, 085\,829\,22 \\ 120.\, 130\,672\,44 \\ 464.\, 783\,498\,34 \end{array} \right ]\end{aligned}\]Ya que estamos hablando de poblaciones, necesitaríamos redondear estos números para dar una respuesta lógica. Por lo tanto, podemos decir que después de\(10\) unidades de tiempo, habrá\(115\) residentes en la ubicación uno,\(120\) en la ubicación dos, y\(465\) en la ubicación tres.

Una segunda aplicación importante de las matrices de Markov es el concepto de caminatas aleatorias. Supongamos que un andador tiene\(m\) ubicaciones para elegir, denotadas\(1, 2, \cdots, m\). Vamos a\(a_{ij}\) referir a la probabilidad de que la persona viajará a la ubicación\(i\) desde la ubicación\(j\). Nuevamente, esto requiere que\[\sum_{i=1}^{k}a_{ij}=1\nonumber\] En este contexto, el vector\(X_n=\left [ x_{1n} \cdots x_{mn}\right ] ^{T}\) contenga las probabilidades de que\(x_{in}\) el caminante termine en ubicación en\(i, 1\leq i \leq m\) el momento\(n\).

Ejemplo\(\PageIndex{6}\): Random Walks

Supongamos que existen tres ubicaciones, referidas como ubicaciones\(1, 2\) y\(3\). La matriz de probabilidades de Markov\(A = [a_{ij}]\) viene dada por\[\left [ \begin{array}{rrr} 0.4 & 0.1 & 0.5 \\ 0.4 & 0.6 & 0.1 \\ 0.2 & 0.3 & 0.4 \end{array} \right ]\nonumber\] Si el andador comienza en ubicación\(1\), calcule la probabilidad de que termine en ubicación en\(3\) el momento\(n = 2\).

Solución

Desde que el andador comienza en ubicación\(1\), tenemos\[X_{0} = \left [ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right ]\nonumber\] El objetivo es calcular\(x_{32}\). Para ello calculamos\(X_{2}\), utilizando\(X_{n+1} = AX_{n}\). \[\begin{aligned} X_{1} &= A X_{0} \\ &= \left [ \begin{array}{rrr} 0.4 & 0.1 & 0.5 \\ 0.4 & 0.6 & 0.1 \\ 0.2 & 0.3 & 0.4 \end{array} \right ] \left [ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right ] \\ &= \left [ \begin{array}{r} 0.4 \\ 0.4 \\ 0.2 \end{array} \right ] \\\end{aligned}\]\[\begin{aligned} X_{2} &= A X_{1} \\ &= \left [ \begin{array}{rrr} 0.4 & 0.1 & 0.5 \\ 0.4 & 0.6 & 0.1 \\ 0.2 & 0.3 & 0.4 \end{array} \right ] \left [ \begin{array}{c} 0.4 \\ 0.4 \\ 0.2 \end{array} \right ] \\ &= \left [ \begin{array}{r} 0.3 \\ 0.42 \\ 0.28 \end{array} \right ] \\\end{aligned}\]Esto da las probabilidades de que nuestro andador termine en las ubicaciones 1, 2 y 3. Para este ejemplo nos interesa la ubicación 3, con una probabilidad encendida\(0.28\).

Volviendo al contexto de migración, supongamos que deseamos saber cuántos residentes estarán en un lugar determinado después de mucho tiempo. Resulta que si algún poder de la matriz migratoria tiene todas las entradas positivas, entonces hay un vector\(X_s\) tal que se\(A^{n}X_{0}\) acerca\(X_s\) como\(n\) se vuelve muy grande. De ahí que a medida que pase más tiempo y\(n\) aumente,\(A^{n}X_{0}\) se acercará más al vector\(X_s\).

Considerar el teorema\(\PageIndex{2}\). Vamos a\(n\) aumentar para que se\(X_n\) acerque\(X_s\). A\(X_n\) medida que se acerca\(X_s\), también lo hace\(X_{n+1}\). Para suficientemente grande\(n\), la declaración\(X_{n+1} = AX_n\) puede escribirse como\(X_s = AX_s\).

Esta discusión motiva el siguiente teorema.

Teorema\(\PageIndex{3}\): Steady State Vector

Dejar\(A\) ser una matriz de migración. Entonces existe un vector de estado estacionario escrito de\(X_s\) tal manera que\[X_s = AX_s\nonumber \] donde\(X_s\) tiene entradas positivas que tienen la misma suma que las entradas de\(X_0\).

A medida que\(n\) aumenta, los vectores de estado\(X_n\) se acercarán\(X_s\).

Obsérvese que la condición en Teorema se\(\PageIndex{3}\) puede escribir como\((I - A)X_s=0\), representando un sistema homogéneo de ecuaciones.

Considera el siguiente ejemplo. Observe que es el mismo ejemplo que el Ejemplo\(\PageIndex{5}\) pero aquí implicará un marco de tiempo más largo.

Ejemplo\(\PageIndex{7}\): Populations over the Long Run

Considerar la matriz de migración\[A = \left [ \begin{array}{rrr} .6 & 0 & .1 \\ .2 & .8 & 0 \\ .2 & .2 & .9 \end{array} \right ]\nonumber \] para ubicaciones\(1,2,\) y\(3.\) Supongamos inicialmente hay 100 residentes en la ubicación 1, 200 en la ubicación 2 y 400 en la ubicación 4. Encuentra la población en las tres localidades después de mucho tiempo.

Solución

Por teorema\(\PageIndex{3}\) el vector de estado estacionario se\(X_s\) puede encontrar resolviendo el sistema\((I-A)X_s = 0\).

Por lo tanto, necesitamos encontrar una solución a\[\left( \left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right ] -\left [ \begin{array}{rrr} .6 & 0 & .1 \\ .2 & .8 & 0 \\ .2 & .2 & .9 \end{array} \right ] \right) \left [ \begin{array}{c} x_{1s} \\ x_{2s}\\ x_{3s} \end{array} \right ] =\left [ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right ]\nonumber \] La matriz aumentada y la forma de escalón de fila-escalón reducida resultante están dadas por\[\left [ \begin{array}{rrr|r} 0.4 & 0 & -0.1 & 0 \\ -0.2 & 0.2 & 0 & 0 \\ -0.2 & -0.2 & 0.1 & 0 \end{array} \right ] \rightarrow \cdots \rightarrow \left [ \begin{array}{rrr|r} 1 & 0 & -0.25 & 0 \\ 0 & 1 & -0.25 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right ]\nonumber\] Por lo tanto, los vectores propios son\[t\left [ \begin{array}{c} 0.25 \\ 0.25 \\ 1 \end{array} \right ]\nonumber\]

El vector inicial\(X_0\) viene dado por\[\left [ \begin{array}{r} 100 \\ 200 \\ 400 \end{array} \right ]\nonumber\]

Ahora todo lo que queda es elegir el valor de\(t\) tal que\[0.25t+0.25t+t=100+200+400\nonumber\] Resolver esta ecuación para\(t\) rendimientos\(t= \ \frac{1400}{3}\). Por lo tanto, la población a la larga viene dada por\[ \ \frac{1400}{3}\left [ \begin{array}{c} 0.25 \\ 0.25 \\ 1 \end{array} \right ] = \left [ \begin{array}{c} 116. 666\,666\,666\, 666\,7 \\ 116. 666\,666\,666\, 666\,7 \\ 466. 666\,666\,666\, 666\,7 \end{array} \right ]\nonumber\]

Nuevamente, debido a que estamos trabajando con poblaciones, estos valores necesitan ser redondeados. El vector de estado estacionario\(X_s\) viene dado por\[\left [ \begin{array}{c} 117 \\ 117 \\ 466 \end{array} \right ]\nonumber\]

Podemos ver que los números que calculamos en Ejemplo\(\PageIndex{5}\) para las poblaciones después de la\(10^{th}\) unidad de tiempo no están lejos de los valores a largo plazo.

Considera otro ejemplo.

Ejemplo\(\PageIndex{8}\): Populations After a Long Time

Supongamos que una matriz de migración viene dada por\[A = \left [ \begin{array}{ccc} \ \frac{1}{5} & \ \frac{1}{2} & \ \frac{1}{5} \\ \ \frac{1}{4} & \ \frac{1}{4} & \ \frac{1}{2} \\ \ \frac{11}{20} & \ \frac{1}{4} & \ \frac{3}{10} \end{array} \right ]\nonumber\] Encontrar la comparación entre las poblaciones en las tres localidades después de un largo tiempo.

Solución

Para comparar las poblaciones a largo plazo, queremos encontrar el vector de estado estacionario\(X_s\). Resolver\[\left( \left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right ] -\left [ \begin{array}{ccc} \ \frac{1}{5} & \ \frac{1}{2} & \ \frac{1}{5} \\ \ \frac{1}{4} & \ \frac{1}{4} & \ \frac{1}{2} \\ \ \frac{11}{20} & \ \frac{1}{4} & \ \frac{3}{10} \end{array} \right ] \right) \left [ \begin{array}{c} x_{1s} \\ x_{2s} \\ x_{3s} \end{array} \right ] =\left [ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right ]\nonumber\] La matriz aumentada y la forma de escalón de fila-escalón reducida resultante están dadas por\[\left [ \begin{array}{rrr|r} \ \frac{4}{5} & - \ \frac{1}{2} & - \ \frac{1}{5} & 0 \\ - \ \frac{1}{4} & \ \frac{3}{4} & - \ \frac{1}{2} & 0 \\ - \ \frac{11}{20} & - \ \frac{1}{4} & \ \frac{7}{10} & 0 \end{array} \right ] \rightarrow \cdots \rightarrow \left [ \begin{array}{rrr|r} 1 & 0 & - \ \frac{16}{19} & 0 \\ 0 & 1 & - \ \frac{18}{19} & 0 \\ 0 & 0 & 0 & 0 \end{array} \right ]\nonumber\] y así un vector propio es\[\left [ \begin{array}{c} 16 \\ 18 \\ 19 \end{array} \right ]\nonumber\]

Por lo tanto, la proporción de población en la ubicación 2 a la ubicación 1 viene dada por\( \ \frac{18}{16}\). La proporción de población 3 a ubicación 2 viene dada por\( \ \frac{19}{18}\).

Valores propios de Matrices de Markov

La siguiente es una proposición importante.

Proposición\(\PageIndex{1}\): Eigenvalues of a Migration Matrix

Dejar\(A=\left [ a_{ij}\right ]\) ser una matriz de migración. Entonces siempre\(1\) es un valor propio para\(A.\)

Prueba

Recuerde que el determinante de una matriz siempre es igual al de su transposición. Por lo tanto,\[\det \left( \lambda I - A\right) =\det \left( \left( \lambda I - A\right) ^{T}\right) =\det \left( \lambda I - A^T\right)\nonumber\] porque\(I^{T}=I.\) Así la ecuación característica para\(A\) es la misma que la ecuación característica para\(A^{T}\). En consecuencia,\(A\) y\(A^{T}\) tienen los mismos valores propios. Mostraremos que\(1\) es un valor propio para\(A^{T}\) y luego seguirá que\(1\) es un valor propio para\(A\).

Recuerda que para una matriz de migración,\(\sum_{i}a_{ij}=1.\) Por lo tanto, si\(A^{T}=\left [ b_{ij}\right ]\) con\(b_{ij}=a_{ji},\) ello se deduce que\[\sum_{j}b_{ij}=\sum_{j}a_{ji}=1\nonumber\]

Por lo tanto, de la multiplicación matricial,\[A^{T}\left [ \begin{array}{r} 1 \\ \vdots \\ 1 \end{array} \right ] =\left [ \begin{array}{c} \sum_{j}b_{ij} \\ \vdots \\ \sum_{j}b_{ij} \end{array} \right ] =\left [ \begin{array}{r} 1 \\ \vdots \\ 1 \end{array} \right ]\nonumber\]

Observe que esto demuestra que\(\left [ \begin{array}{r} 1 \\ \vdots \\ 1 \end{array} \right ]\) es un autovector para\(A^{T}\) corresponder al autovalor,\(\lambda =1.\) Como se explicó anteriormente, esto muestra que\(\lambda =1\) es un valor propio para\(A\) porque\(A\) y\(A^{T}\) tienen los mismos valores propios.

Sistemas Dinámicos

Las matrices de migración discutidas anteriormente dan un ejemplo de un sistema dinámico discreto. Los llamamos discretos porque involucran valores discretos tomados en una secuencia de puntos en lugar de en un intervalo de tiempo continuo.

Un ejemplo de una situación que se puede estudiar de esta manera es un modelo de presa depredadora. Considera el siguiente modelo donde\(x\) está el número de presas y\(y\) el número de depredadores en un área determinada en un momento determinado. Estas son funciones de\(n\in \mathbb{N}\) dónde\(n=1,2,\cdots\) están los fines de intervalos de tiempo que pueden ser de interés en el problema. En otras palabras,\(x \left( n \right)\) es el número de presas al final del\(n^{th}\) intervalo de tiempo. Un ejemplo de esta situación puede ser modelado por la siguiente ecuación\[\left [ \begin{array}{c} x\left( n+1\right) \\ y\left( n+1\right) \end{array} \right ] =\left [ \begin{array}{rr} 2 & -3 \\ 1 & 4 \end{array} \right ] \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\nonumber\] Esto dice que de periodo de tiempo\(n\) a\(n+1\),\(x\) aumenta si hay más\(x\) y disminuye a medida que hay más\(y\). En el contexto de este ejemplo, esto significa que a medida que aumenta el número de depredadores, el número de presas disminuye. En cuanto\(y,\) a que aumenta si hay más\(y\) y también si hay más\(x\).

Este es un ejemplo de una recurrencia matricial que definimos ahora.

Definición\(\PageIndex{2}\): Matrix Recurrence

Supongamos que un sistema dinámico viene dado por\[\begin{aligned} x_{n+1} &= a x_n + b y_n \\ y_{n+1} &= c x_n + d y_n\end{aligned}\]

Este sistema se puede expresar como\(V_{n+1} = A V_{n}\) dónde\(V_{n} = \left [ \begin{array}{r} x_n \\ y_n \end{array} \right ]\) y\(A = \left [ \begin{array}{rr} a & b \\ c & d \end{array} \right ]\).

En esta sección, examinaremos cómo encontrar soluciones a un sistema dinámico dadas ciertas condiciones iniciales. Este proceso involucra varios conceptos previamente estudiados, entre ellos la diagonalización matricial y las matrices de Markov. El procedimiento se da de la siguiente manera. Recordemos que cuando se diagonaliza, podemos escribir\(A^{n} = PD^{n}P^{-1}\).

Procedimiento\(\PageIndex{1}\): Solving a Dynamical System

Supongamos que un sistema dinámico viene dado por\[\begin{aligned} x_{n+1} &= a x_n + b y_n \\ y_{n+1} &= c x_n + d y_n\end{aligned}\]

Dadas las condiciones iniciales\(x_0\) y\(y_0\), las soluciones al sistema se encuentran de la siguiente manera:

1. Exprese el sistema dinámico en la forma\(V_{n+1} = AV_n\).
2. Diagonalizar\(A\) para ser escrito como\(A = PDP^{-1}\).
3. Entonces\(V_{n} = PD^{n} P^{-1} V_{0}\) donde\(V_{0}\) esta el vector que contiene las condiciones iniciales.
4. Si se le dan valores específicos para\(n\), sustituya en esta ecuación. De lo contrario, encuentre una solución general para\(n\).

Consideraremos ahora un ejemplo en detalle.

Ejemplo\(\PageIndex{9}\): Solutions of a Discrete Dynamical System

Supongamos que un sistema dinámico viene dado por\[\begin{aligned} x_{n+1} &= 1.5 x_n - 0.5y_n\\ y_{n+1} &= 1.0 x_n\end{aligned}\]

Expresar este sistema como una recurrencia matricial y encontrar soluciones al sistema dinámico para las condiciones iniciales\(x_0=20, y_0=10\).

Solución

Primero, expresamos el sistema como una recurrencia matricial. \[\begin{aligned} V_{n+1} &= AV_{n}\\ \left [ \begin{array}{c} x\left( n+1\right) \\ y\left( n+1\right) \end{array} \right ] &=\left [ \begin{array}{rr} 1.5 & -0.5 \\ 1.0 & 0 \end{array} \right ] \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\end{aligned}\]

Entonces\[A = \left [ \begin{array}{rr} 1.5 & -0.5 \\ 1.0 & 0 \end{array} \right ]\nonumber \] podrás verificar que los valores propios de\(A\) son\(1\) y\(.5\). Al diagonalizar, podemos escribir\(A\) en el formulario\[P^{-1} D P = \left [ \begin{array}{rr} 1 & 1 \\ 1 & 2 \end{array} \right ] \left [ \begin{array}{rr} 1 & 0 \\ 0 & .5 \end{array} \right ] \left [ \begin{array}{rr} 2 & -1 \\ -1 & 1 \end{array} \right ]\nonumber\]

Ahora dada una condición inicial,\[V_0 = \left [ \begin{array}{c} x_{0} \\ y_{0} \end{array} \right ]\nonumber\] la solución al sistema dinámico viene dada por\[\begin{aligned} V_n &= P D^n P^{-1} V_0\\ \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ] &=\left [ \begin{array}{rr} 1 & 1 \\ 1 & 2 \end{array} \right ] \left [ \begin{array}{rr} 1 & 0 \\ 0 & .5 \end{array} \right ] ^{n}\left [ \begin{array}{rr} 2 & -1 \\ -1 & 1 \end{array} \right ] \left [ \begin{array}{c} x_{0} \\ y_{0} \end{array} \right ] \\ &=\left [ \begin{array}{rr} 1 & 1 \\ 1 & 2 \end{array} \right ] \left [ \begin{array}{rr} 1 & 0 \\ 0 & \left( .5\right) ^{n} \end{array} \right ] \left [ \begin{array}{rr} 2 & -1 \\ -1 & 1 \end{array} \right ] \left [ \begin{array}{c} x_{0} \\ y_{0} \end{array} \right ] \\ &=\left [ \begin{array}{c} y_{0}\left( \left( .5\right) ^{n}-1\right) -x_{0}\left( \left( .5\right) ^{n}-2\right) \\ y_{0}\left( 2\left( .5\right) ^{n}-1\right) -x_{0}\left( 2\left( .5\right) ^{n}-2\right) \end{array} \right ] \end{aligned}\]

Si dejamos que\(n\) se vuelvan arbitrariamente grandes, este vector se acerca\[\left [ \begin{array}{c} 2x_{0}-y_{0} \\ 2x_{0}-y_{0} \end{array} \right ]\nonumber\]

Por lo tanto, para grandes\(n,\)\[\left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ] \approx \left [ \begin{array}{c} 2x_{0}-y_{0} \\ 2x_{0}-y_{0} \end{array} \right ]\nonumber\]

Ahora supongamos que la condición inicial viene dada por\[\left [ \begin{array}{c} x_{0} \\ y_{0} \end{array} \right ] = \left [ \begin{array}{r} 20 \\ 10 \end{array} \right ]\nonumber\]

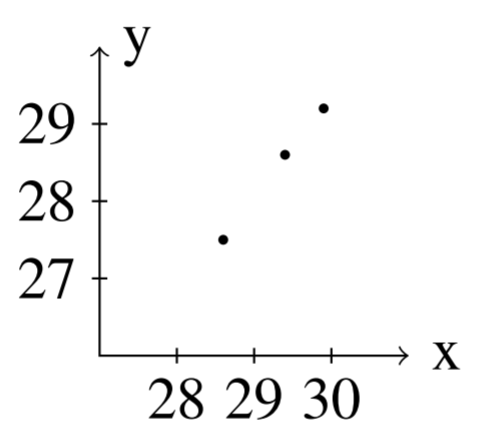
Entonces, podemos encontrar soluciones para diversos valores de\(n\). Aquí están las soluciones para valores de\(n\) entre\(1\) y\(5\)\[n=1: \left [ \begin{array}{r} 25.0 \\ 20.0 \end{array} \right ], n=2: \left [ \begin{array}{r} 27.5 \\ 25.0 \end{array} \right ], n=3: \left [ \begin{array}{r} 28.75 \\ 27.5 \end{array} \right ]\nonumber\]\[n=4: \left [ \begin{array}{r} 29.375 \\ 28.75 \end{array} \right ], n=5: \left [ \begin{array}{r} 29.688 \\ 29.375 \end{array} \right ]\nonumber\]

Observe que a medida que\(n\) aumenta, nos acercamos al vector dado por\[\left [ \begin{array}{c} 2x_{0}-y_{0} \\ 2x_{0}-y_{0} \end{array} \right ] = \left [ \begin{array}{r} 2\left(20\right)- 10\\ 2\left( 20 \right)-10 \end{array} \right ] = \left [ \begin{array}{r} 30\\ 30 \end{array} \right ]\nonumber\]

Estas soluciones se grafican en la siguiente figura.

Figura\(\PageIndex{1}\)

El siguiente ejemplo demuestra otro sistema que exhibe algún comportamiento interesante. Cuando graficamos las soluciones, es posible que los pares ordenados se desplieguen en espiral alrededor del origen.

Ejemplo\(\PageIndex{10}\): Finding Solutions to a Dynamical System

Supongamos que un sistema dinámico es de la forma\[\left [ \begin{array}{c} x\left( n+1\right) \\ y\left( n+1\right) \end{array} \right ] =\left [ \begin{array}{rr} 0.7 & 0.7 \\ -0.7 & 0.7 \end{array} \right ] \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\nonumber \] Encontrar soluciones al sistema dinámico para condiciones iniciales dadas.

Solución

Dejar\[A = \left [ \begin{array}{rr} 0.7 & 0.7 \\ -0.7 & 0.7 \end{array} \right ]\nonumber\] Para encontrar soluciones, debemos diagonalizar\(A\). Se puede verificar que los valores propios de\(A\) son complejos y están dados por\(\lambda_1 = .7+.7i\) y\(\lambda_2 = .7-.7i\). El vector propio para\(\lambda_1 = .7+.7i\) es\[\left [ \begin{array}{r} 1 \\ i \end{array} \right ]\nonumber\] y para el que el vector propio\(\lambda_2 = .7-.7i\) es\[\left [ \begin{array}{r} 1 \\ -i \end{array} \right ]\nonumber\]

Así la matriz se\(A\) puede escribir en la forma\[\left [ \begin{array}{rr} 1 & 1 \\ i & -i \end{array} \right ] \left [ \begin{array}{cc} .7+.7i & 0 \\ 0 & .7-.7i \end{array} \right ] \left [ \begin{array}{rr} \frac{1}{2} & - \frac{1}{2}i \\ \frac{1}{2} & \frac{1}{2}i \end{array} \right ]\nonumber\] y así,\[\begin{aligned} V_n &= PD^nP^{-1}V_0 \\ \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ] &=\left [ \begin{array}{rr} 1 & 1 \\ i & -i \end{array} \right ] \left [ \begin{array}{cc} \left( .7+.7i\right) ^{n} & 0 \\ 0 & \left( .7-.7i\right) ^{n} \end{array} \right ] \left [ \begin{array}{rr} \frac{1}{2} & - \frac{1}{2}i \\ \frac{1}{2} & \frac{1}{2}i \end{array} \right ] \left [ \begin{array}{c} x_{0} \\ y_{0} \end{array} \right ]\end{aligned}\]

La solución explícita viene dada por\[\left [ \begin{array}{c} x_{0}\left( \frac{1}{2}\left( 0.7-0.7i \right) ^{n}+ \frac{1}{2} \left( 0.7+0.7i\right) ^{n}\right) + y_{0}\left( \frac{1}{2} i\left( 0.7-0.7i\right) ^{n}-\frac{1}{2}i \left( 0.7+0.7i\right) ^{n}\right) \\ y_{0}\left( \frac{1}{2} \left( 0.7-0.7i \right) ^{n}+ \frac{1}{2} \left( 0.7+0.7i\right) ^{n}\right) - x_{0}\left( \frac{1}{2} i\left( 0.7-0.7i\right) ^{n}- \frac{1}{2}i\left( 0.7+0.7i\right) ^{n}\right) \end{array} \right ]\nonumber\]

Supongamos que la condición inicial es\[\left [ \begin{array}{c} x_{0} \\ y_{0} \end{array} \right ] =\left [ \begin{array}{r} 10 \\ 10 \end{array} \right ]\nonumber\] Entonces se obtiene la siguiente secuencia de valores que se grafican a continuación dejando\(n=1,2,\cdots ,20\)

Figura\(\PageIndex{2}\)

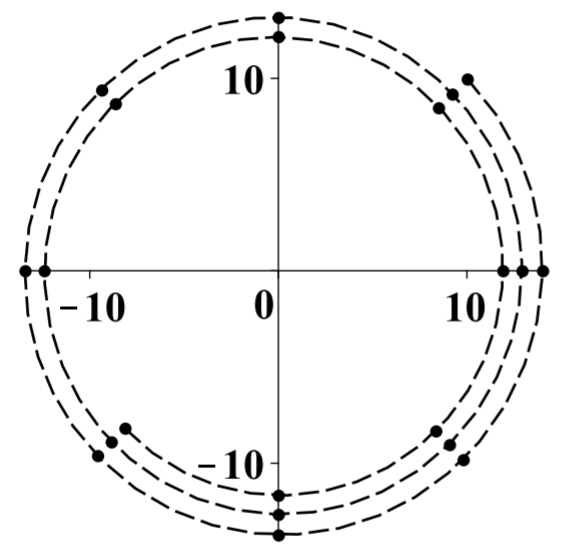
En esta imagen, los puntos son los valores y la línea discontinua es para ayudar a imaginar lo que está sucediendo.

Estos puntos se van acercando poco a poco al origen, pero van dando vueltas al origen en el sentido de las agujas del reloj a medida que lo hacen. A medida\(n\) que aumenta, el vector\(\left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\) se acerca\(\left [ \begin{array}{r} 0 \\ 0 \end{array} \right ]\)

Este tipo de comportamiento junto con valores propios complejos es típico de las desviaciones de un punto de equilibrio en el sistema Lotka Volterra de ecuaciones diferenciales que es un modelo famoso para las interacciones depredador-presa. Estas ecuaciones diferenciales vienen dadas por\[\begin{aligned} x^{\prime } &=x\left( a-by\right) \\ y^{\prime } &=-y\left( c-dx\right)\end{aligned}\] donde\(a,b,c,d\) están las constantes positivas. Por ejemplo, podrías\(X\) haber sido la población de alces y\(Y\) la población de lobos en una isla.

Tenga en cuenta que estas ecuaciones tienen sentido lógico. El tope dice que la tasa a la que aumenta la población de alces sería\(aX\) si no hubiera depredadores\(Y\). Sin embargo, esto se modifica multiplicando en su lugar por\(\left( a-bY\right)\) porque si hay depredadores, estos militarán contra la población de alces. Cuantos más depredadores haya, más pronunciado es este efecto. En cuanto a la ecuación del depredador, se puede ver que las ecuaciones predicen que si hay muchas presas alrededor, entonces la tasa de crecimiento de los depredadores parecería ser alta. Sin embargo, esto se ve modificado por el término\(-cY\) porque si hay muchos depredadores, habría competencia por el suministro de alimentos disponible y esto tendería a disminuir\(Y^{\prime }.\)

El comportamiento cerca de un punto de equilibrio, que es un punto donde el lado derecho de las ecuaciones diferenciales es igual a cero, es de gran interés. En este caso, el punto de equilibrio es\[x=\frac{c}{d}, y=\frac{a}{b}\nonumber\] Entonces se definen nuevas variables según la fórmula\[x+\frac{c}{d}=x,\ y=y+\frac{a}{b}\nonumber\] En términos de estas nuevas variables, las ecuaciones diferenciales se vuelven\[\begin{aligned} x^{\prime } &=\left( x+\frac{c}{d}\right) \left( a-b\left( y+\frac{a}{b} \right) \right) \\ y^{\prime } &=-\left( y+\frac{a}{b}\right) \left( c-d\left( x+\frac{c}{d} \right) \right)\end{aligned}\] Multiplicando los rendimientos de los lados derechos\[\begin{aligned} x^{\prime } &=-bxy-b\frac{c}{d}y \\ y^{\prime } &=dxy+\frac{a}{b}dx\end{aligned}\] El interés es para\(x,y\) pequeños y así estas ecuaciones son esencialmente igual a\[x^{\prime }=-b\frac{c}{d}y,\ y^{\prime }=\frac{a}{b}dx\nonumber\]

Reemplazar\(x^{\prime }\) con el cociente de diferencia\(\frac{x\left( t+h\right) -x\left( t\right) }{h}\) donde\(h\) es un número positivo pequeño y\(y^{\prime }\) con un cociente de diferencia similar. Por ejemplo uno podría haber\(h\) correspondido a un día o incluso a una hora. Así, para lo suficientemente\(h\) pequeño, la siguiente parecería ser una buena aproximación a las ecuaciones diferenciales. \[\begin{aligned} x\left( t+h\right) &=x\left( t\right) -hb\frac{c}{d}y \\ y\left( t+h\right) &=y\left( t\right) +h\frac{a}{b}dx\end{aligned}\]Dejar\(1,2,3,\cdots\) denotar los extremos de intervalos discretos de tiempo teniendo duración\(h\) elegida anteriormente. Entonces las ecuaciones anteriores toman la forma\[\left [ \begin{array}{c} x\left( n+1\right) \\ y\left( n+1\right) \end{array} \right ] =\left [ \begin{array}{cc} 1 & - \frac{hbc}{d} \\ \frac{had}{b} & 1 \end{array} \right ] \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\nonumber\] Tenga en cuenta que los valores propios de esta matriz son siempre complejos.

No nos interesan los intervalos de tiempo de duración\(h\) para\(h\) muy pequeños. En cambio, estamos interesados en periodos de tiempo mucho más largos. De esta manera, reemplazando el intervalo de tiempo por\(mh,\)\[\left [ \begin{array}{c} x\left( n+m\right) \\ y\left( n+m\right) \end{array} \right ] =\left [ \begin{array}{cc} 1 & - \frac{hbc}{d} \\ \frac{had}{b} & 1 \end{array} \right ] ^{m}\left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\nonumber\] Por ejemplo, si\(m=2,\) tendrías en\[\left [ \begin{array}{c} x\left( n+2\right) \\ y\left( n+2\right) \end{array} \right ] =\left [ \begin{array}{cc} 1-ach^{2} & -2b \frac{c}{d}h \\ 2 \frac{a}{b}dh & 1-ach^{2} \end{array} \right ] \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\nonumber\] cuenta que la mayor parte del tiempo, los valores propios de la nueva matriz serán complejos.

También puedes notar que la esquina superior derecha será negativa al considerar potencias superiores de la matriz. Así, dejando\(1,2,3,\cdots\) denotar los extremos de intervalos discretos de tiempo, el sistema dinámico discreto deseado es de la forma\[\left [ \begin{array}{c} x\left( n+1\right) \\ y\left( n+1\right) \end{array} \right ] =\left [ \begin{array}{rr} a & -b \\ c & d \end{array} \right ] \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ]\nonumber\] donde\(a,b,c,d\) están constantes positivas y la matriz probablemente tendrá valores propios complejos porque es una potencia de una matriz que tiene valores propios complejos.

Se puede ver de la discusión anterior que si los valores propios de la matriz utilizada para definir el sistema dinámico son menores de 1 en valor absoluto, entonces el origen es estable en el sentido de que a medida que\(n\rightarrow \infty ,\) la solución converge con el origen. Si cualquiera de los valores propios es mayor que 1 en valor absoluto, entonces las soluciones al sistema dinámico generalmente estarán sin límites, a menos que la condición inicial se elija con mucho cuidado. El siguiente ejemplo muestra el caso en el que un valor propio es mayor que 1 y el otro es menor que 1.

El siguiente ejemplo demuestra un concepto familiar como sistema dinámico.

Ejemplo\(\PageIndex{11}\): The Fibonacci Sequence

La secuencia de Fibonacci es la secuencia dada por la\[1, 1, 2, 3, 5, \cdots\nonumber\] cual se define recursivamente en la forma\[x\left( 0\right) =1=x\left( 1\right) ,\ x\left( n+2\right) =x\left( n+1\right) +x\left( n\right)\nonumber\] Mostrar cómo la Secuencia de Fibonacci puede considerarse un sistema dinámico.

Solución

Esta secuencia es sumamente importante en el estudio de los conejos reproductores. Se puede considerar como un sistema dinámico de la siguiente manera. Let\(y\left( n\right) =x\left( n+1\right) .\) Entonces la relación de recurrencia anterior se puede escribir como\[\left [ \begin{array}{c} x\left( n+1\right) \\ y\left( n+1\right) \end{array} \right ] =\left [ \begin{array}{rr} 0 & 1 \\ 1 & 1 \end{array} \right ] \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ] ,\ \left [ \begin{array}{c} x\left( 0\right) \\ y\left( 0\right) \end{array} \right ] =\left [ \begin{array}{r} 1 \\ 1 \end{array} \right ]\nonumber \]

Let\[A = \left [ \begin{array}{rr} 0 & 1 \\ 1 & 1 \end{array} \right ]\nonumber \]

Los valores propios de la matriz\(A\) son\(\lambda_1 = \frac{1}{2}-\frac{1}{2}\sqrt{5}\) y\(\lambda_2 = \frac{1}{2}\sqrt{5}+\frac{1}{2}\). Los vectores propios correspondientes son, respectivamente,\[X_1 = \left [ \begin{array}{c} - \frac{1}{2}\sqrt{5}- \frac{1}{2} \\ 1 \end{array} \right ] , X_2 = \left [ \begin{array}{c} \frac{1}{2}\sqrt{5}- \frac{1}{2} \\ 1 \end{array} \right ]\nonumber \]

Se puede ver a partir de un cálculo corto que uno de los valores propios es menor que 1 en valor absoluto mientras que el otro es mayor que 1 en valor absoluto. Ahora, la diagonalización nos\(A\) da\[\left [ \begin{array}{cc} \frac{1}{2}\sqrt{5}- \frac{1}{2} & - \frac{1}{2}\sqrt{5}- \frac{1}{2} \\ 1 & 1 \end{array} \right ] ^{-1}\left [ \begin{array}{rr} 0 & 1 \\ 1 & 1 \end{array} \right ] \left [ \begin{array}{cc} \frac{1}{2}\sqrt{5}- \frac{1}{2} & - \frac{1}{2}\sqrt{5}- \frac{1}{2} \\ 1 & 1 \end{array} \right ]\nonumber \]\[=\left [ \begin{array}{cc} \frac{1}{2}\sqrt{5}+ \frac{1}{2} & 0 \\ 0 & \frac{1}{2}- \frac{1}{2}\sqrt{5} \end{array} \right ]\nonumber \]

Entonces se deduce que para una condición inicial dada, la solución a este sistema dinámico es de la forma\[\begin{aligned} \left [ \begin{array}{c} x\left( n\right) \\ y\left( n\right) \end{array} \right ] &=\left [ \begin{array}{cc} \frac{1}{2}\sqrt{5}- \frac{1}{2} & - \frac{1}{2}\sqrt{5}- \frac{1}{2} \\ 1 & 1 \end{array} \right ] \left [ \begin{array}{cc} \left( \frac{1}{2}\sqrt{5}+ \frac{1}{2}\right) ^{n} & 0 \\ 0 & \left( \frac{1}{2}- \frac{1}{2}\sqrt{5}\right) ^{n} \end{array} \right ] \cdot \\ &\left [ \begin{array}{cc} \frac{1}{5}\sqrt{5} & \frac{1}{10}\sqrt{5}+ \frac{1}{2} \\ - \frac{1}{5}\sqrt{5} & \frac{1}{5}\sqrt{5}\left( \frac{1}{2}\sqrt{5}- \frac{1 }{2}\right) \end{array} \right ] \left [ \begin{array}{r} 1 \\ 1 \end{array} \right ]\end{aligned}\] Se deduce que\[x\left( n\right) =\left( \frac{1}{2}\sqrt{5}+\frac{1}{2}\right) ^{n}\left( \frac{1}{10}\sqrt{5}+\frac{1}{2}\right) +\left( \frac{1}{2}-\frac{1}{2}\sqrt{5}\right) ^{n}\left( \frac{1}{2}-\frac{1}{10}\sqrt{5}\right)\nonumber \]

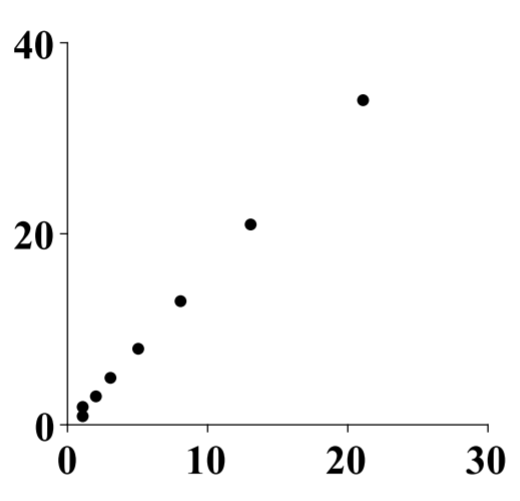
Aquí hay una imagen de los pares ordenados\(\left( x\left( n\right) ,y\left( n\right) \right)\) para\(n=0,1,\cdots ,n\).

Figura\(\PageIndex{3}\)

Hay mucho más de lo que se puede decir sobre los sistemas dinámicos. Es un tema importante de estudio en ecuaciones diferenciales y lo que se da anteriormente es solo una introducción.

La Matriz Exponencial

El objetivo de esta sección es utilizar el concepto de la matriz exponencial para resolver ecuaciones diferenciales lineales de primer orden. Comenzamos por probar la matriz exponencial.

Supongamos que\(A\) es una matriz diagonalizable. Entonces la matriz exponencial, escrita\(e^{A}\), se puede definir fácilmente. Recordemos que si\(D\) es una matriz diagonal, entonces\[P^{-1}AP=D\nonumber \]\(D\) es de la forma\[\left [ \begin{array}{ccc} \lambda _{1} & & 0 \\ & \ddots & \\ 0 & & \lambda _{n} \end{array} \right ] \label{diagonalmatrix}\] y se deduce que\[D^{m}=\left [ \begin{array}{ccc} \lambda _{1}^{m} & & 0 \\ & \ddots & \\ 0 & & \lambda _{n}^{m} \end{array} \right ]\nonumber \]

Dado que\(A\) es diagonalizable,\[A=PDP^{-1}\nonumber \] y\[A^{m}=PD^{m}P^{-1}\nonumber \]

Recordemos por qué esto es cierto. \[A=PDP^{-1}\nonumber \]y así\[\begin{aligned} A^{m} &=\overset{ \text{m times}}{\overbrace{PDP^{-1}PDP^{-1}PDP^{-1}\cdots PDP^{-1}}} \\ &=PD^{m}P^{-1}\end{aligned}\]

Ahora vamos a examinar qué se entiende por la matriz exponental\(e^{A}\). Comience por escribir formalmente la siguiente serie de poder para\(e^{A}\):\[e^{A} = \sum_{k=0}^{\infty }\frac{A^{k}}{k!}=\sum_{k=0}^{\infty }\frac{PD^{k}P^{-1}}{k!}=P \left( \sum_{k=0}^{\infty }\frac{D^{k}}{k!} \right)P^{-1}\nonumber \] Si\(D\) se da arriba en\(\eqref{diagonalmatrix}\), la suma anterior es de la forma\[P \left( \sum_{k=0}^{\infty }\left [ \begin{array}{ccc} \frac{1}{k!}\lambda _{1}^{k} & & 0 \\ & \ddots & \\ 0 & & \frac{1}{k!}\lambda _{n}^{k} \end{array} \right ] \right) P^{-1}\nonumber \] Esto se puede reorganizar de la siguiente manera:\[e^{A}=P\left [ \begin{array}{ccc} \sum_{k=0}^{\infty }\frac{1}{k!}\lambda _{1}^{k} & & 0 \\ & \ddots & \\ 0 & & \sum_{k=0}^{\infty }\frac{1}{k!}\lambda _{n}^{k} \end{array} \right ] P^{-1}\nonumber \]\[=P\left [ \begin{array}{ccc} e^{\lambda _{1}} & & 0 \\ & \ddots & \\ 0 & & e^{\lambda _{n}} \end{array} \right ] P^{-1}\nonumber \]

Esto justifica el siguiente teorema.

Teorema\(\PageIndex{4}\): The Matrix Exponential

Dejar\(A\) ser una matriz diagonalizable, con valores propios\(\lambda_1, ..., \lambda_n\) y matriz correspondiente de vectores propios\(P\). Entonces la matriz exponencial,\(e^{A}\), viene dada por\[e^{A} = P\left [ \begin{array}{ccc} e^{\lambda _{1}} & & 0 \\ & \ddots & \\ 0 & & e^{\lambda _{n}} \end{array} \right ] P^{-1}\nonumber \]

Ejemplo\(\PageIndex{12}\): Compute \(e^A\) for a Matrix \(A\)

Vamos a\[A=\left [ \begin{array}{rrr} 2 & -1 & -1 \\ 1 & 2 & 1 \\ -1 & 1 & 2 \end{array} \right ]\nonumber \] encontrar\(e^{A}\).

Solución

Los valores propios funcionan para ser\(1,2,3\) y los vectores propios asociados con estos valores propios son\[\left [ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right ] \leftrightarrow 1, \left [ \begin{array}{r} -1 \\ -1 \\ 1 \end{array} \right ] \leftrightarrow 2,\left [ \begin{array}{r} -1 \\ 0 \\ 1 \end{array} \right ] \leftrightarrow 3\nonumber \] Entonces let\[D=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{array} \right ], P=\left [ \begin{array}{rrr} 0 & -1 & -1 \\ -1 & -1 & 0 \\ 1 & 1 & 1 \end{array} \right ]\nonumber \] y así\[P^{-1}=\left [ \begin{array}{rrr} 1 & 0 & 1 \\ -1 & -1 & -1 \\ 0 & 1 & 1 \end{array} \right ]\nonumber \]

Entonces la matriz exponencial es\[e^{At} = \left [ \begin{array}{rrr} 0 & -1 & -1 \\ -1 & -1 & 0 \\ 1 & 1 & 1 \end{array} \right ] \left [ \begin{array}{ccc} e^{1} & 0 & 0 \\ 0 & e^{2} & 0 \\ 0 & 0 & e^{3} \end{array} \right ] \left [ \begin{array}{rrr} 1 & 0 & 1 \\ -1 & -1 & -1 \\ 0 & 1 & 1 \end{array} \right ]\nonumber \]\[\left [ \begin{array}{ccc} e^{2} & e^{2}-e^{3} & e^{2}-e^{3} \\ e^{2}-e & e^{2} & e^{2}-e \\ -e^{2}+e & -e^{2}+e^{3} & -e^{2}+e+e^{3} \end{array} \right ]\nonumber \]

La matriz exponencial es una herramienta útil para resolver sistemas autónomos de ecuaciones diferenciales lineales de primer orden. Estas son ecuaciones que son de la forma\[X^{\prime }=AX, X(0) = C\nonumber \] donde\(A\) es una\(n\times n\) matriz diagonalizable y\(C\) es un vector constante. \(X\)es un vector de funciones en una variable,\(t\):\[X = X(t) = \left [ \begin{array}{c} x_1(t) \\ x_2(t) \\ \vdots \\ x_n(t) \end{array} \right ]\nonumber \] Luego\(X^{\prime }\) se refiere a la primera derivada de\(X\) y está dada por\[X^{\prime} = X^{\prime}(t) = \left [ \begin{array}{c} x_1^{\prime}(t) \\ x_2^{\prime}(t) \\ \vdots \\ x_n^{\prime}(t) \end{array} \right ], \; x_i^{\prime}(t) = \text{the derivative of}\; x_i(t)\nonumber \]

Entonces resulta que la solución al anterior sistema de ecuaciones es\(X\left( t\right) =e^{At}C\). Para ver esto, supongamos que\(A\) es diagonalizable para que\[A=P\left [ \begin{array}{ccc} \lambda _{1} & & \\ & \ddots & \\ & & \lambda _{n} \end{array} \right ] P^{-1}\nonumber \] Entonces\[e^{At}=P\left [ \begin{array}{ccc} e^{\lambda _{1}t} & & \\ & \ddots & \\ & & e^{\lambda _{n}t} \end{array} \right ] P^{-1}\nonumber \]\[e^{At}C=P\left [ \begin{array}{ccc} e^{\lambda _{1}t} & & \\ & \ddots & \\ & & e^{\lambda _{n}t} \end{array} \right ] P^{-1}C\nonumber \]

Diferenciar\(e^{At}C\) rendimientos\[X^{\prime} = \left( e^{At}C\right) ^{\prime }=P\left [ \begin{array}{ccc} \lambda _{1}e^{\lambda _{1}t} & & \\ & \ddots & \\ & & \lambda _{n}e^{\lambda _{n}t} \end{array} \right ] P^{-1}C\nonumber \]\[=P\left [ \begin{array}{ccc} \lambda _{1} & & \\ & \ddots & \\ & & \lambda _{n} \end{array} \right ] \left [ \begin{array}{ccc} e^{\lambda _{1}t} & & \\ & \ddots & \\ & & e^{\lambda _{n}t} \end{array} \right ] P^{-1}C\nonumber \]\[\begin{aligned} &=P\left [ \begin{array}{ccc} \lambda _{1} & & \\ & \ddots & \\ & & \lambda _{n} \end{array} \right ] P^{-1}P\left [ \begin{array}{ccc} e^{\lambda _{1}t} & & \\ & \ddots & \\ & & e^{\lambda _{n}t} \end{array} \right ] P^{-1}C \\ &=A\left( e^{At}C\right) = AX\end{aligned}\] Por lo tanto,\(X = X(t) = e^{At}C\) es una solución a\(X^{\prime }=AX\).

Para probar que\(X(0) = C\) si\(X(t) = e^{At}C\):\[X(0) = e^{A0}C=P\left [ \begin{array}{ccc} 1 & & \\ & \ddots & \\ & & 1 \end{array} \right ] P^{-1}C=C\nonumber \]

Ejemplo\(\PageIndex{13}\): Solving an Initial Value Problem

Resolver el problema de valor inicial\[\left [ \begin{array}{c} x \\ y \end{array} \right ] ^{\prime }=\left [ \begin{array}{rr} 0 & -2 \\ 1 & 3 \end{array} \right ] \left [ \begin{array}{c} x \\ y \end{array} \right ] ,\ \left [ \begin{array}{c} x(0)\\ y(0) \end{array} \right ] =\left [ \begin{array}{c} 1 \\ 1 \end{array} \right ]\nonumber \]

Solución

La matriz es diagonalizable y se puede escribir como\[\begin{aligned} A &= PDP^{-1} \\ \left [ \begin{array}{rr} 0 & -2 \\ 1 & 3 \end{array} \right ] &=\left [ \begin{array}{rr} 1 & 1 \\ -\frac{1}{2} & -1 \end{array} \right ] \left [ \begin{array}{rr} 1 & 0 \\ 0 & 2 \end{array} \right ] \left [ \begin{array}{rr} 2 & 2 \\ -1 & -2 \end{array} \right ]\end{aligned}\] Por lo tanto, la matriz exponencial es de la forma\[e^{At} = \left [ \begin{array}{rr} 1 & 1 \\ -\frac{1}{2} & -1 \end{array} \right ] \left [ \begin{array}{cc} e^{t} & 0 \\ 0 & e^{2t} \end{array} \right ] \left [ \begin{array}{rr} 2 & 2 \\ -1 & -2 \end{array} \right ]\nonumber \] La solución al problema de valor inicial es\[\begin{aligned} X(t) &= e^{At}C \\ \left [ \begin{array}{c} x\left( t\right) \\ y\left( t\right) \end{array} \right ] &= \left [ \begin{array}{rr} 1 & 1 \\ -\frac{1}{2} & -1 \end{array} \right ] \left [ \begin{array}{cc} e^{t} & 0 \\ 0 & e^{2t} \end{array} \right ] \left [ \begin{array}{rr} 2 & 2 \\ -1 & -2 \end{array} \right ] \left [ \begin{array}{c} 1 \\ 1 \end{array} \right ] \\ &=\left [ \begin{array}{c} 4e^{t}-3e^{2t} \\ 3e^{2t}-2e^{t} \end{array} \right ]\end{aligned}\] Podemos comprobar que esto funciona:\[\begin{aligned} \left [ \begin{array}{c} x\left( 0\right) \\ y\left( 0\right) \end{array} \right ] &= \left [ \begin{array}{c} 4e^{0}-3e^{2(0)} \\ 3e^{2(0)}-2e^{0} \end{array} \right ] \\ &= \left [ \begin{array}{c} 1 \\ 1 \end{array} \right ]\end{aligned}\]

Por último,\[X^{\prime} = \left [ \begin{array}{c} 4e^{t}-3e^{2t} \\ 3e^{2t}-2e^{t} \end{array} \right ] ^{\prime }=\left [ \begin{array}{c} 4e^{t}-6e^{2t} \\ 6e^{2t}-2e^{t} \end{array} \right ]\nonumber \] y\[AX = \left [ \begin{array}{rr} 0 & -2 \\ 1 & 3 \end{array} \right ] \left [ \begin{array}{c} 4e^{t}-3e^{2t} \\ 3e^{2t}-2e^{t} \end{array} \right ] =\left [ \begin{array}{c} 4e^{t}-6e^{2t} \\ 6e^{2t}-2e^{t} \end{array} \right ]\nonumber \] que es lo mismo. Así esta es la solución al problema del valor inicial.