7.4: Ortogonalidad
- Page ID
- 114831
Diagonalización ortogonal
Comenzamos esta sección recordando algunas definiciones importantes. Recordemos de la Definición 4.11.4 que los vectores distintos de cero se denominan ortogonales si su producto de punto es igual\(0\). Un conjunto es ortonormal si es ortogonal y cada vector es un vector unitario.
Una matriz ortogonal\(U\), de la Definición 4.11.7, es aquella en la que\(UU^{T} = I\). En otras palabras, la transposición de una matriz ortogonal es igual a su inversa. Una característica clave de las matrices ortogonales, que será esencial en esta sección, es que las columnas de una matriz ortogonal forman un conjunto ortonormal.
Ahora recordamos otra definición importante.
Una\(n\times n\) matriz real\(A,\) es simétrica\(A^{T}=A.\) si\( A=-A^{T},\) entonces\(A\) se llama simétrica sesgada.
Antes de probar un teorema esencial, primero examinamos el siguiente lema que se utilizará a continuación.
Dejemos\(A=\left ( a_{ij} \right )\) ser una verdadera\(n \times n\) matriz simétrica, y dejar\(\vec{x}, \vec{y} \in \mathbb{R}^n\). Entonces\[A\vec{x} \cdot \vec{y} = \vec{x} \cdot A \vec{y}\nonumber\]
- Prueba
-
Este resultado se desprende de la definición del producto punto junto con las propiedades de multiplicación matricial, de la siguiente manera:\[\begin{aligned} A\vec{x} \cdot \vec{y} &= \sum_{k,l}a_{kl}x_{l}y_{k} \\ &=\sum_{k,l} (a_{lk})^Tx_{l}y_{k} \\ &= \vec{x}\cdot A^{T}\vec{y} \\ &= \vec{x}\cdot A \vec{y}\end{aligned}\]
El último paso se desprende de\(A^T = A\), ya que\(A\) es simétrico.
Ahora podemos probar que los valores propios de una matriz simétrica real son números reales. Considera el siguiente teorema importante.
\(A\)Sea una verdadera matriz simétrica. Entonces los valores propios de\(A\) son números reales y los vectores propios correspondientes a valores propios distintos son ortogonales.
- Prueba
-
Recordemos que para un número complejo\(a+ib,\) el conjugado complejo, denotado por\(\overline{a+ib}\) está dado por\(\overline{a+ib}=a-ib.\) La notación,\(\overline{\vec{x}}\) denotará el vector que tiene cada entrada reemplazada por su conjugado complejo.
Supongamos que\(A\) es una matriz simétrica real y\(A\vec{x}=\lambda \vec{x}\). Entonces\[\overline{\lambda \vec{x}}^{T}\vec{x}=\left( \overline{A \vec{x}}\right) ^{T}\vec{x}=\overline{\vec{x}}^{T}A^{T}\vec{x}= \overline{\vec{x}}^{T}A\vec{x}=\lambda \overline{\vec{x}}^{T} \vec{x}\nonumber \] Dividir por ambos\(\overline{\vec{x}}^{T}\vec{x}\) lados rinde\(\overline{\lambda }=\lambda\) lo que dice\(\lambda\) es real. Para ello, tenemos que asegurarnos de eso\(\overline{\vec{x}}^{T}\vec{x} \neq 0\). Observe que\(\overline{\vec{x}}^{T}\vec{x} = 0\) si y solo si\(\vec{x} = \vec{0}\). Ya que elegimos\(\vec{x}\) tal que\(A\vec{x} = \lambda \vec{x}\),\(\vec{x}\) es un vector propio y por lo tanto debe ser distinto de cero.
Ahora supongamos que\(A\) es real simétrico y\(A\vec{x}=\lambda \vec{x}\),\(A \vec{y}=\mu \vec{y}\) dónde\(\mu \neq \lambda\). Entonces como\(A\) es simétrico, se deduce de Lemma\(\PageIndex{1}\) sobre el producto punto que\[\lambda \vec{x}\cdot \vec{y}=A\vec{x}\cdot \vec{y}=\vec{x}\cdot A\vec{y}=\vec{x}\cdot \mu \vec{y}=\mu \vec{x}\cdot \vec{y}\nonumber \] De ahí\(\left( \lambda -\mu \right) \vec{x}\cdot \vec{y}=0.\) se deduce que,\(\lambda -\mu \neq 0,\) ya que debe ser eso\(\vec{x}\cdot \vec{y}=0\). Por lo tanto, los vectores propios forman un conjunto ortogonal.
El siguiente teorema se demuestra de manera similar.
Los valores propios de una matriz simétrica de sesgo real son iguales\(0\) o son números imaginarios puros.
- Prueba
-
Primero, tenga en cuenta que si\(A=0\) es la matriz cero, entonces\(A\) es simétrica sesgada y tiene valores propios iguales a\(0\).
Supongamos\(A=-A^{T}\) que así\(A\) es sesgar simétrico y\(A\vec{x}=\lambda \vec{x}\). Entonces\[\overline{\lambda \vec{x}}^{T}\vec{x}=\left( \overline{A \vec{x}}\right) ^{T}\vec{x}=\overline{\vec{x}}^{T}A^{T}\vec{x}=- \overline{\vec{x}}^{T}A\vec{x}=-\lambda \overline{\vec{x}}^{T} \vec{x}\nonumber \] y así, dividiendo por\(\overline{\vec{x}}^{T}\vec{x}\) como antes,\(\overline{\lambda }=-\lambda .\) Dejar que\(\lambda =a+ib,\) esto significa\(a-ib=-a-ib\) y así\(a=0.\) Así\(\lambda\) es puro imaginario.
Considera el siguiente ejemplo.
Vamos\(A=\left[ \begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array} \right] .\) a encontrar sus valores propios.
Solución
Primer aviso que\(A\) es simétrico sesgado. Por teorema\(\PageIndex{2}\), los valores propios serán iguales\(0\) o serán puros imaginarios. Los valores propios de\(A\) se obtienen resolviendo la ecuación habitual\[\det (\lambda I - A ) = \det \left[ \begin{array}{rr} \lambda & 1 \\ -1 & \lambda \end{array} \right] =\lambda ^{2}+1=0\nonumber \]
De ahí que los valores propios sean\(\pm i,\) puros imaginarios.
Considera el siguiente ejemplo.
Vamos\(A=\left[ \begin{array}{rr} 1 & 2 \\ 2 & 3 \end{array} \right] .\) a encontrar sus valores propios.
Solución
Primero, fíjate que\(A\) es simétrico. Por teorema\(\PageIndex{1}\), los valores propios serán todos reales. Los valores propios de\(A\) se obtienen resolviendo la ecuación\[\det (\lambda I - A) = \det \left[ \begin{array}{rr} \lambda - 1 & -2 \\ -2 & \lambda - 3 \end{array} \right] = \lambda^2 -4\lambda -1=0\nonumber \] habitual Los valores propios están dados por\(\lambda_1 =2+ \sqrt{5}\) y\(\lambda_2 =2-\sqrt{5}\) que son ambos reales.
Recordemos que una matriz diagonal\(D=\left ( d_{ij} \right )\) es aquella en la que\(d_{ij} = 0\) siempre\(i \neq j\). En otras palabras, todos los números que no están en la diagonal principal son iguales a cero.
Considera el siguiente teorema importante.
\(A\)Sea una verdadera matriz simétrica. Entonces existe una matriz ortogonal\(U\) tal que\[U^{T}AU = D\nonumber \] donde\(D\) es una matriz diagonal. Además, las entradas diagonales de\(D\) son los valores propios de\(A\).
Podemos usar este teorema para diagonalizar una matriz simétrica, utilizando matrices ortogonales. Considera el siguiente corolario.
Si\(A\) es una matriz\(n\times n\) simétrica real, entonces existe un conjunto ortonormal de vectores propios,\(\left\{ \vec{u}_{1},\cdots ,\vec{u} _{n}\right\} .\)
- Prueba
-
Ya que\(A\) es simétrica, entonces por Teorema\(\PageIndex{3}\), existe una matriz ortogonal\(U\) tal que\(U^{T}AU=D,\) una matriz diagonal cuyas entradas diagonales son los valores propios de\(A.\) Por lo tanto, ya que\(A\) es simétrica y todas las matrices son reales,\[\overline{D}=\overline{D^{T}}=\overline{U^{T}A^{T}U}=U^{T}A^{T}U=U^{T}AU=D\nonumber \] mostrando \(D\)es real porque cada entrada de\(D\) equivale a su complejo conjugado.
Ahora vamos\[U=\left[ \begin{array}{cccc} \vec{u}_{1} & \vec{u}_{2} & \cdots & \vec{u}_{n} \end{array} \right]\nonumber \] donde\(\vec{u}_{i}\) denotan las columnas de\(U\) y\[D=\left[ \begin{array}{ccc} \lambda _{1} & & 0 \\ & \ddots & \\ 0 & & \lambda _{n} \end{array} \right]\nonumber \] La ecuación,\(U^{T}AU=D\) implica\(AU = UD\) y\[\begin{aligned} AU &=\left[ \begin{array}{cccc} A\vec{u}_{1} & A\vec{u}_{2} & \cdots & A\vec{u}_{n} \end{array} \right] \\ &=\left[ \begin{array}{cccc} \lambda _{1}\vec{u}_{1} & \lambda _{2}\vec{u}_{2} & \cdots & \lambda _{n}\vec{u}_{n} \end{array} \right] \\ &= UD\end{aligned}\] donde las entradas denotan las columnas de\(AU\) y\(UD\) respectivamente. Por lo tanto,\(A\vec{u}_{i}=\lambda _{i}\vec{u}_{i}\). Dado que la matriz\(U\) es ortogonal, la\(ij^{th}\) entrada de\(U^{T}U\) iguales\(\delta _{ij}\) y así\[\delta _{ij}=\vec{u}_{i}^{T}\vec{u}_{j}=\vec{u}_{i}\cdot \vec{u} _{j}\nonumber \] Esto prueba el corolario porque muestra que los vectores\(\left\{ \vec{u} _{i}\right\}\) forman un conjunto ortonormal.
\(A\)Déjese ser una\(n \times n\) matriz. Entonces los ejes principales de\(A\) es un conjunto de vectores propios ortonormales de\(A\).
En el siguiente ejemplo, examinamos cómo encontrar tal conjunto de vectores propios ortonormales.
Buscar un conjunto ortonormal de vectores propios para la matriz simétrica\[A = \left[ \begin{array}{rrr} 17 & -2 & -2 \\ -2 & 6 & 4 \\ -2 & 4 & 6 \end{array} \right]\nonumber \]
Solución
Recordar Procedimiento 7.1.1 para encontrar los valores propios y vectores propios de una matriz. Puedes verificar que los valores propios son\(18,9,2.\) Primero encuentra el vector propio para\(18\) resolviendo la ecuación\((18I-A)X = 0\). La matriz aumentada apropiada viene dada por\[\left[ \begin{array}{ccc|c} 18-17 & 2 & 2 & 0 \\ 2 & 18-6 & -4 & 0 \\ 2 & -4 & 18-6 & 0 \end{array} \right]\nonumber \] La forma reducida de fila-escalón es\[\left[ \begin{array}{rrr|r} 1 & 0 & 4 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] Por lo tanto, un vector propio es\[\left[ \begin{array}{r} -4 \\ 1 \\ 1 \end{array} \right]\nonumber \] Siguiente encontrar el vector propio para\(\lambda =9.\) La matriz aumentada y la forma de escalón de fila reducida resultante son\[\left[ \begin{array}{ccc|c} 9-17 & 2 & 2 & 0 \\ 2 & 9-6 & -4 & 0 \\ 2 & -4 & 9-6 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & - \frac{1}{2} & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] Así, un vector propio para\(\lambda =9\) es\[\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right]\nonumber \] Finalmente encuentra un vector propio para\(\lambda =2.\) La matriz aumentada apropiada y la forma de escalón de fila reducida son\[\left[ \begin{array}{ccc|c} 2-17 & 2 & 2 & 0 \\ 2 & 2-6 & -4 & 0 \\ 2 & -4 & 2-6 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] Así, un vector propio para\(\lambda =2\) es\[\left[ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right]\nonumber \]
El conjunto de vectores propios para\(A\) viene dado por\[\left\{ \left[ \begin{array}{r} -4 \\ 1 \\ 1 \end{array} \right], \left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right], \left[ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right] \right\}\nonumber \] Puede verificar que estos vectores propios forman un conjunto ortogonal. Al dividir cada vector propio por su magnitud, obtenemos un conjunto ortonormal:\[\left\{ \frac{1}{\sqrt{18}}\left[ \begin{array}{r} -4 \\ 1 \\ 1 \end{array} \right] ,\frac{1}{3}\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right] ,\frac{1}{\sqrt{2}}\left[ \begin{array}{r} 0 \\ -1 \\ 1 \end{array} \right] \right\}\nonumber \]
Considera el siguiente ejemplo.
Encontrar un conjunto ortonormal de tres vectores propios para la matriz\[A = \left[ \begin{array}{rrr} 10 & 2 & 2 \\ 2 & 13 & 4 \\ 2 & 4 & 13 \end{array} \right]\nonumber \]
Solución
Se puede verificar que los valores propios de\(A\) son\(9\) (con multiplicidad dos) y\(18\) (con multiplicidad uno). Considera los vectores propios correspondientes a\(\lambda =9\). La matriz aumentada apropiada y la forma fila-escalón reducida están dadas por\[\left[ \begin{array}{ccc|c} 9-10 & -2 & -2 & 0 \\ -2 & 9-13 & -4 & 0 \\ -2 & -4 & 9-13 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 2 & 2 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] y así los vectores propios son de la forma\[\left[ \begin{array}{c} -2y-2z \\ y \\ z \end{array} \right]\nonumber \] Necesitamos encontrar dos de estos que son ortogonales. Que se dé uno por el ajuste\(z=0\) y\(y=1\), dando\(\left[ \begin{array}{r} -2 \\ 1 \\ 0 \end{array} \right]\).
Para encontrar un autovector ortogonal a éste, necesitamos satisfacer\[\left[ \begin{array}{r} -2 \\ 1 \\ 0 \end{array} \right] \cdot \left[ \begin{array}{c} -2y-2z \\ y \\ z \end{array} \right] =5y+4z=0\nonumber \] Los valores\(y=-4\) y\(z=5\) satisfacer esta ecuación, dando otro vector propio correspondiente a\(\lambda=9\) como\[\left[ \begin{array}{c} -2\left( -4\right) -2\left( 5\right) \\ \left( -4\right) \\ 5 \end{array} \right] =\left[ \begin{array}{r} -2 \\ -4 \\ 5 \end{array} \right]\nonumber \] Siguiente encontrar el vector propio para\(\lambda =18.\) La matriz aumentada y la fila reducida resultante- forma escalón son dados por\[\left[ \begin{array}{ccc|c} 18-10 & -2 & -2 & 0 \\ -2 & 18-13 & -4 & 0 \\ -2 & -4 & 18-13 & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & - \frac{1}{2} & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] y así un vector propio es\[\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right]\nonumber \]
Dividiendo cada vector propio por su longitud, el conjunto ortonormal es\[\left\{ \frac{1}{\sqrt{5}} \left[ \begin{array}{r} -2\\ 1 \\ 0 \end{array} \right] , \frac{\sqrt{5}}{15} \left[ \begin{array}{r} -2 \\ -4 \\ 5 \end{array} \right] , \frac{1}{3}\left[ \begin{array}{r} 1 \\ 2 \\ 2 \end{array} \right] \right\}\nonumber \]
En la solución anterior, el valor propio repetido implica que habría habido muchas otras bases ortonormales que podrían haberse obtenido. Si bien elegimos tomar\(z=0, y=1\), podríamos haber tomado con la misma facilidad\(y=0\) o incluso\(y=z=1.\) Cualquier cambio de este tipo habría resultado en un conjunto ortonormal diferente.
Recordemos la siguiente definición.
Se dice que una\(n\times n\) matriz no\(A\) es defectuosa o diagonalizable si existe una matriz invertible\(P\) tal que\(P^{-1}AP=D\) donde\(D\) está una matriz diagonal.
Como se indica en Teorema\(\PageIndex{3}\) si\(A\) es una matriz simétrica real, existe una matriz ortogonal\(U\) tal que\(U^{T}AU=D\) donde\(D\) es una matriz diagonal. Por lo tanto, toda matriz simétrica es diagonalizable porque si\(U\) es una matriz ortogonal, es invertible y su inversa es\(U^{T}\). En este caso, decimos que\(A\) es ortogonalmente diagonalizable. Por lo tanto, cada matriz simétrica es de hecho ortogonalmente diagonalizable. El siguiente teorema proporciona otra forma de determinar si una matriz es ortogonalmente diagonalizable.
\(A\)Déjese ser una\(n \times n\) matriz. Entonces\(A\) es ortogonalmente diagonalizable si y solo si\(A\) tiene un conjunto ortonormal de vectores propios.
Recordemos de Corolario\(\PageIndex{1}\) que cada matriz simétrica tiene un conjunto ortonormal de vectores propios. De hecho estas tres condiciones son equivalentes.
En el siguiente ejemplo, se\(U\) encontrará que la matriz ortogonal diagonaliza ortogonalmente una matriz.
Vamos\(A=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{3}{2} \end{array} \right] .\) Encuentra una matriz ortogonal\(U\) tal que\(U^{T}AU\) sea una matriz diagonal.
Solución
En este caso, los valores propios son\(2\) (con multiplicidad uno) y\(1\) (con multiplicidad dos). Primero encontraremos un vector propio para el valor propio\(2\). La matriz aumentada apropiada y la forma de escalón de fila reducida resultante están dadas por\[\left[ \begin{array}{ccc|c} 2-1 & 0 & 0 & 0 \\ 0 & 2- \frac{3}{2} & - \frac{1}{2} & 0 \\ 0 & - \frac{1}{2} & 2- \frac{3}{2} & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 1 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] y así un autovector es\[\left[ \begin{array}{r} 0 \\ 1 \\ 1 \end{array} \right]\nonumber \] Sin embargo, se desea que los vectores propios sean vectores unitarios y así dividir este vector por su longitud da\[\left[ \begin{array}{c} 0 \\ \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right]\nonumber \] Siguiente encontrar los vectores propios correspondientes al valor propio igual a\(1\). La matriz aumentada apropiada y la forma de escalón reducida resultante están dadas por:\[\left[ \begin{array}{ccc|c} 1-1 & 0 & 0 & 0 \\ 0 & 1- \frac{3}{2} & - \frac{1}{2} & 0 \\ 0 & - \frac{1}{2} & 1- \frac{3}{2} & 0 \end{array} \right] \rightarrow \cdots \rightarrow \left[ \begin{array}{rrr|r} 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right]\nonumber \] Por lo tanto, los vectores propios son de la forma\[\left[ \begin{array}{r} s \\ -t \\ t \end{array} \right]\nonumber \] Dos de estos que son ortonormales son\(\left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right]\), eligiendo\(s=1\) y\(t=0\), y\(\left[ \begin{array}{c} 0 \\ - \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \right]\), dejando\(s=0\),\(t= 1\) y normalizando el vector resultante.
Para obtener la matriz ortogonal deseada, dejamos que los autovectores ortonormales calculados anteriormente sean las columnas. \[\left[ \begin{array}{rrr} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right]\nonumber \]
Para verificar, computar de la\(U^{T}AU\) siguiente manera:\[U^{T}AU = \left[ \begin{array}{rrr} 0 & - \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ 1 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array} \right] \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{3}{2} \end{array} \right] \left[ \begin{array}{rrr} 0 & 1 & 0 \\ -\frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array} \right]\nonumber \]\[=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right] = D\nonumber \] la matriz diagonal deseada. Observe que los vectores propios, que construyen las columnas de\(U\), están en el mismo orden que los autovalores en\(D\).
Concluimos esta sección con un Teorema que generaliza resultados anteriores.
\(A\)Déjese ser una\(n \times n\) matriz. Si\(A\) tiene valores propios\(n\) reales, entonces se\(U\) puede encontrar una matriz ortogonal para dar como resultado la matriz triangular superior\(U^T A U\).
triangulación
Este Teorema proporciona un Corolario útil.
Dejar\(A\) ser una\(n \times n\) matriz con valores propios\(\lambda_1, \cdots, \lambda_n\). Entonces se deduce que\(\det(A)\) es igual al producto de la\(\lambda_i\), mientras que\(trace(A)\) es igual a la suma de la\(\lambda_i\).
- Prueba
-
Por Teorema\(\PageIndex{5}\), existe una matriz ortogonal\(U\) tal que\(U^TAU=P\), donde\(P\) se encuentra una matriz triangular superior. Dado que\(P\) es similar a\(A\), los valores propios de\(P\) son\(\lambda_1, \lambda_2, \ldots, \lambda_n\). Además, dado que\(P\) es triangular (superior), las entradas en la diagonal principal de\(P\) son sus valores propios, así\(\det(P)=\lambda_1 \lambda_2 \cdots \lambda_n\) y\(trace(P)=\lambda_1 + \lambda_2 + \cdots + \lambda_n\). Ya que\(P\) y\(A\) son similares,\(\det(A)=\det(P)\) y\(trace(A)=trace(P)\), y por lo tanto siguen los resultados.
La descomposición del valor singular
Comenzamos esta sección con una definición importante.
\(A\)Déjese ser una\(m\times n\) matriz. Los valores singulares de\(A\) son las raíces cuadradas de los valores propios positivos de\(A^TA.\)
La descomposición de valores singulares (SVD) puede considerarse como una generalización de la diagonalización ortogonal de una matriz simétrica a una\(m\times n\) matriz arbitraria. Esta descomposición es el foco de esta sección.
El siguiente es un resultado útil que ayudará a la hora de calcular la SVD de matrices.
\(A\)Déjese ser una\(m \times n\) matriz. Entonces\(A^TA\) y\(AA^T\) tener los mismos valores propios distintos de cero.
- Prueba
-
Supongamos que\(A\) es una\(m\times n\) matriz, y supongamos que\(\lambda\) es un valor propio distinto de cero de\(A^TA\). Entonces existe un vector distinto de cero\(X\in \mathbb{R}^n\) tal que\[\label{nonzero} (A^TA)X=\lambda X.\]
Multiplicar ambos lados de esta ecuación por\(A\) rendimientos:\[\begin{aligned} A(A^TA)X & = A\lambda X\\ (AA^T)(AX) & = \lambda (AX).\end{aligned}\] Desde\(\lambda\neq 0\) y\(X\neq 0_n\),\(\lambda X\neq 0_n\), y por lo tanto por ecuación\(\eqref{nonzero}\),\((A^TA)X\neq 0_m\); así\(A^T(AX)\neq 0_m\), implicando eso\(AX\neq 0_m\).
Por lo tanto,\(AX\) es un vector propio de\(AA^T\) correspondiente al valor propio\(\lambda\). Se puede utilizar un argumento análogo para mostrar que cada valor propio distinto de cero de\(AA^T\) es un valor propio de\(A^TA\), completando así la prueba.
Dada una\(m\times n\) matriz\(A\), veremos cómo expresar\(A\) como un producto\[A=U\Sigma V^T\nonumber \] donde
- \(U\)es una matriz\(m\times m\) ortogonal cuyas columnas son vectores propios de\(AA^T\).
- \(V\)es una matriz\(n\times n\) ortogonal cuyas columnas son vectores propios de\(A^TA\).
- \(\Sigma\)es una\(m\times n\) matriz cuyos únicos valores distintos de cero se encuentran en su diagonal principal, y son los valores singulares de\(A\).
¿Cómo podemos encontrar tal descomposición? Nuestro objetivo es descomponerse\(A\) de la siguiente forma:
\[A=U\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] V^T\nonumber \]donde\(\sigma\) esta de la forma\[\sigma =\left[ \begin{array}{ccc} \sigma _{1} & & 0 \\ & \ddots & \\ 0 & & \sigma _{k} \end{array} \right]\nonumber \]
Así\(A^T=V\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] U^T\) y se deduce que\[A^TA=V\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] U^TU\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right] V^T=V\left[ \begin{array}{cc} \sigma ^{2} & 0 \\ 0 & 0 \end{array} \right] V^T\nonumber \] y así\(A^TAV=V\left[ \begin{array}{cc} \sigma ^{2} & 0 \\ 0 & 0 \end{array} \right] .\) Del mismo modo,\(AA^TU=U\left[ \begin{array}{cc} \sigma ^{2} & 0 \\ 0 & 0 \end{array} \right] .\) por lo tanto, encontrarías una base ortonormal de vectores propios para\(AA^T\) hacerlos las columnas de una matriz tal que los valores propios correspondientes estén disminuyendo. Esto da\(U.\) Podrías entonces hacer lo mismo\(A^TA\) para conseguir\(V\).
Formalizamos esta discusión en el siguiente teorema.
\(A\)Déjese ser una\(m\times n\) matriz. Luego existen matrices ortogonales\(U\) y\(V\) del tamaño apropiado tal que\(A= U \Sigma V^T\) donde\(\Sigma\) es de la forma\[\Sigma = \left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right]\nonumber \] y\(\sigma\) es de la forma\[\sigma =\left[ \begin{array}{ccc} \sigma _{1} & & 0 \\ & \ddots & \\ 0 & & \sigma _{k} \end{array} \right]\nonumber \] para\(\sigma _{i}\) los valores singulares de\(A.\)
- Prueba
-
Existe una base ortonormal,\(\left\{ \vec{v}_{i}\right\} _{i=1}^{n}\) tal que\(A^TA\vec{v}_{i}=\sigma _{i}^{2}\vec{v}_{i}\) donde\(\sigma _{i}^{2}>0\) para\(i=1,\cdots ,k,\left( \sigma _{i}>0\right)\) y es igual a cero si\(i>k.\) Así para\(i>k,\)\(A\vec{v}_{i}=\vec{0}\) porque\[A\vec{v}_{i}\cdot A\vec{v}_{i} = A^TA\vec{v}_{i} \cdot \vec{v}_{i} = \vec{0} \cdot \vec{v}_{i} =0.\nonumber \] Para\(i=1,\cdots ,k,\) definir\(\vec{u}_{i}\in \mathbb{R}^{m}\) por\[\vec{u}_{i}= \sigma _{i}^{-1}A\vec{v}_{i}.\nonumber \]
Así\(A\vec{v}_{i}=\sigma _{i}\vec{u}_{i}.\) Ahora\[\begin{aligned} \vec{u}_{i} \cdot \vec{u}_{j} &= \sigma _{i}^{-1}A \vec{v}_{i} \cdot \sigma _{j}^{-1}A\vec{v}_{j} = \sigma_{i}^{-1}\vec{v}_{i} \cdot \sigma _{j}^{-1}A^TA\vec{v}_{j} \\ &= \sigma _{i}^{-1}\vec{v}_{i} \cdot \sigma _{j}^{-1}\sigma _{j}^{2} \vec{v}_{j} = \frac{\sigma _{j}}{\sigma _{i}}\left( \vec{v}_{i} \cdot \vec{v}_{j}\right) =\delta _{ij}.\end{aligned}\] Así\(\left\{ \vec{u}_{i}\right\} _{i=1}^{k}\) es un conjunto ortonormal de vectores en\(\mathbb{R}^{m}.\) También,\[AA^T\vec{u}_{i}=AA^T\sigma _{i}^{-1}A\vec{v}_{i}=\sigma _{i}^{-1}AA^TA\vec{v}_{i}=\sigma _{i}^{-1}A\sigma _{i}^{2}\vec{v} _{i}=\sigma _{i}^{2}\vec{u}_{i}.\nonumber \] Ahora extender\(\left\{ \vec{u}_{i}\right\} _{i=1}^{k}\) a una base ortonormal para todos\(\mathbb{R}^{m},\left\{ \vec{u}_{i}\right\} _{i=1}^{m}\) y dejar\[U= \left[ \begin{array}{ccc} \vec{u}_{1} & \cdots & \vec{u}_{m} \end{array} \right ]\nonumber \] mientras\(V= \left( \vec{v}_{1}\cdots \vec{v}_{n}\right) .\) Así\(U\) es la matriz que tiene las columnas\(\vec{u}_{i}\) as y\(V\) es definido como la matriz que tiene las columnas\(\vec{v}_{i}\) as. Entonces\[U^TAV=\left[ \begin{array}{c} \vec{u}_{1}^T \\ \vdots \\ \vec{u}_{k}^T \\ \vdots \\ \vec{u}_{m}^T \end{array} \right] A\left[ \vec{v}_{1}\cdots \vec{v}_{n}\right]\nonumber \]\[=\left[ \begin{array}{c} \vec{u}_{1}^T \\ \vdots \\ \vec{u}_{k}^T \\ \vdots \\ \vec{u}_{m}^T \end{array} \right] \left[ \begin{array}{cccccc} \sigma _{1}\vec{u}_{1} & \cdots & \sigma _{k}\vec{u}_{k} & \vec{0} & \cdots & \vec{0} \end{array} \right] =\left[ \begin{array}{cc} \sigma & 0 \\ 0 & 0 \end{array} \right]\nonumber \] donde\(\sigma\) se da en el enunciado del teorema.
El valor singular de descomposición tiene como corolario inmediato el cual se da en el siguiente resultado interesante.
\(A\)Déjese ser una\(m\times n\) matriz. Entonces el rango de\(A\) y\(A^T\) es igual al número de valores singulares.
Calculemos la descomposición del valor singular de una matriz simple.
Vamos\(A=\left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right]\). Encuentra la Descomposición del Valor Singular (SVD) de\(A\).
Solución
Para comenzar, calculamos\(AA^T\) y\(A^TA\). \[AA^T = \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] \left[\begin{array}{rr} 1 & 3 \\ -1 & 1 \\ 3 & 1 \end{array}\right] = \left[\begin{array}{rr} 11 & 5 \\ 5 & 11 \end{array}\right].\nonumber \]
\[A^TA = \left[\begin{array}{rr} 1 & 3 \\ -1 & 1 \\ 3 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] = \left[\begin{array}{rrr} 10 & 2 & 6 \\ 2 & 2 & -2\\ 6 & -2 & 10 \end{array}\right].\nonumber \]
Dado que\(AA^T\)\(A^T A\) es\(2\times 2\) while es\(3\times 3\),\(AA^T\) y y\(A^TA\) tienen los mismos valores propios distintos de cero (por Proposición\(\PageIndex{1}\)), calculamos el polinomio característico\(c_{AA^T}(x)\) (porque es más fácil de calcular que\(c_{A^TA}(x)\)).
\[\begin{aligned} c_{AA^T}(x)& = \det(xI-AA^T)= \left|\begin{array}{cc} x-11 & -5 \\ -5 & x-11 \end{array}\right|\\ & = (x-11)^2 - 25 \\ & = x^2-22x+121-25\\ & = x^2-22x+96\\ & = (x-16)(x-6)\end{aligned}\]
Por lo tanto, los valores propios de\(AA^T\) son\(\lambda_1=16\) y\(\lambda_2=6\).
Los valores propios de\(A^TA\) son\(\lambda_1=16\),\(\lambda_2=6\), y\(\lambda_3=0\), y los valores singulares de\(A\) son\(\sigma_1=\sqrt{16}=4\) y\(\sigma_2=\sqrt{6}\). Por convención, enumeramos los valores propios (y los valores singulares correspondientes) en orden no creciente (es decir, de mayor a menor).
Para encontrar la matriz\(V\):
Para construir la matriz\(V\) necesitamos encontrar vectores propios para\(A^TA\). Dado que los valores propios de\(AA^T\) son distintos, los vectores propios correspondientes son ortogonales, y solo necesitamos normalizarlos.
\(\lambda_1=16\): resolver\((16I-A^TA)Y= 0\). \[\left[\begin{array}{rrr|r} 6 & -2 & -6 & 0 \\ -2 & 14 & 2 & 0 \\ -6 & 2 & 6 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], \mbox{ so } Y=\left[\begin{array}{r} t \\ 0 \\ t \end{array}\right] =t\left[\begin{array}{r} 1 \\ 0 \\ 1 \end{array}\right], t\in \mathbb{R}.\nonumber \]
\(\lambda_2=6\): resolver\((6I-A^TA)Y= 0\). \[\left[\begin{array}{rrr|r} -4 & -2 & -6 & 0 \\ -2 & 4 & 2 & 0 \\ -6 & 2 & -4 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], \mbox{ so } Y=\left[\begin{array}{r} -s \\ -s \\ s \end{array}\right] =s\left[\begin{array}{r} -1 \\ -1 \\ 1 \end{array}\right], s\in \mathbb{R}.\nonumber \]
\(\lambda_3=0\): resolver\((-A^TA)Y= 0\). \[\left[\begin{array}{rrr|r} -10 & -2 & -6 & 0 \\ -2 & -2 & 2 & 0 \\ -6 & 2 & -10 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & 0 & 1 & 0 \\ 0 & 1 & -2 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right], \mbox{ so } Y=\left[\begin{array}{r} -r \\ 2r \\ r \end{array}\right] =r\left[\begin{array}{r} -1 \\ 2 \\ 1 \end{array}\right], r\in \mathbb{R}.\nonumber \]
Vamos\[V_1=\frac{1}{\sqrt{2}}\left[\begin{array}{r} 1\\ 0\\ 1 \end{array}\right], V_2=\frac{1}{\sqrt{3}}\left[\begin{array}{r} -1\\ -1\\ 1 \end{array}\right], V_3=\frac{1}{\sqrt{6}}\left[\begin{array}{r} -1\\ 2\\ 1 \end{array}\right].\nonumber \]
Entonces\[V=\frac{1}{\sqrt{6}}\left[\begin{array}{rrr} \sqrt 3 & -\sqrt 2 & -1 \\ 0 & -\sqrt 2 & 2 \\ \sqrt 3 & \sqrt 2 & 1 \end{array}\right].\nonumber \]
También,\[\Sigma = \left[\begin{array}{rrr} 4 & 0 & 0 \\ 0 & \sqrt 6 & 0 \end{array}\right],\nonumber \] y usamos\(A\),\(V^T\), y\(\Sigma\) para encontrar\(U\).
Ya que\(V\) es ortogonal y\(A=U\Sigma V^T\), de ello se deduce que\(AV=U\Sigma\). Dejar\(V=\left[\begin{array}{ccc} V_1 & V_2 & V_3 \end{array}\right]\), y dejar\(U=\left[\begin{array}{cc} U_1 & U_2 \end{array}\right]\), dónde\(U_1\) y\(U_2\) son las dos columnas de\(U\).
Entonces tenemos\[\begin{aligned} A\left[\begin{array}{ccc} V_1 & V_2 & V_3 \end{array}\right] &= \left[\begin{array}{cc} U_1 & U_2 \end{array}\right]\Sigma\\ \left[\begin{array}{ccc} AV_1 & AV_2 & AV_3 \end{array}\right] &= \left[\begin{array}{ccc} \sigma_1U_1 + 0U_2 & 0U_1 + \sigma_2 U_2 & 0 U_1 + 0 U_2 \end{array}\right] \\ &= \left[\begin{array}{ccc} \sigma_1U_1 & \sigma_2 U_2 & 0 \end{array}\right]\end{aligned}\] lo que implica eso\(AV_1=\sigma_1U_1 = 4U_1\) y\(AV_2=\sigma_2U_2 = \sqrt 6 U_2\).
Así,\[U_1 = \frac{1}{4}AV_1 = \frac{1}{4} \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] \frac{1}{\sqrt{2}}\left[\begin{array}{r} 1\\ 0\\ 1 \end{array}\right] = \frac{1}{4\sqrt 2}\left[\begin{array}{r} 4\\ 4 \end{array}\right] = \frac{1}{\sqrt 2}\left[\begin{array}{r} 1\\ 1 \end{array}\right],\nonumber \] y\[U_2 = \frac{1}{\sqrt 6}AV_2 = \frac{1}{\sqrt 6} \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right] \frac{1}{\sqrt{3}}\left[\begin{array}{r} -1\\ -1\\ 1 \end{array}\right] =\frac{1}{3\sqrt 2}\left[\begin{array}{r} 3\\ -3 \end{array}\right] =\frac{1}{\sqrt 2}\left[\begin{array}{r} 1\\ -1 \end{array}\right].\nonumber \] Por lo tanto,\[U=\frac{1}{\sqrt{2}}\left[\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right],\nonumber \] y\[\begin{aligned} A & = \left[\begin{array}{rrr} 1 & -1 & 3 \\ 3 & 1 & 1 \end{array}\right]\\ & = \left(\frac{1}{\sqrt{2}}\left[\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right]\right) \left[\begin{array}{rrr} 4 & 0 & 0 \\ 0 & \sqrt 6 & 0 \end{array}\right] \left(\frac{1}{\sqrt{6}}\left[\begin{array}{rrr} \sqrt 3 & 0 & \sqrt 3 \\ -\sqrt 2 & -\sqrt 2 & \sqrt2 \\ -1 & 2 & 1 \end{array}\right]\right).\end{aligned}\]
Aquí hay otro ejemplo.
Encuentra un SVD para\(A=\left[\begin{array}{r} -1 \\ 2\\ 2 \end{array}\right]\).
Solución
Dado que\(A\)\(A^T A\) es\(3\times 1\), es una\(1\times 1\) matriz cuyos valores propios son más fáciles de encontrar que los valores propios de la\(3\times 3\) matriz\(AA^T\).
\[A^TA=\left[\begin{array}{ccc} -1 & 2 & 2 \end{array}\right] \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right] =\left[\begin{array}{r} 9 \end{array}\right].\nonumber \]
Así\(A^TA\) tiene el valor propio\(\lambda_1=9\), y los valores propios de\(AA^T\) son\(\lambda_1=9\),\(\lambda_2=0\), y\(\lambda_3=0\). Además,\(A\) tiene sólo un valor singular,\(\sigma_1=3\).
Para encontrar la matriz\(V\): Para ello encontramos un vector propio para\(A^TA\) y normalizarlo. En este caso, encontrar un vector propio unitario es trivial:\(V_1=\left[\begin{array}{r} 1 \end{array}\right]\), y\[V=\left[\begin{array}{r} 1 \end{array}\right].\nonumber \]
También,\(\Sigma =\left[\begin{array}{r} 3 \\ 0\\ 0 \end{array}\right]\), y usamos\(A\),\(V^T\), y\(\Sigma\) para encontrar\(U\).
Ahora\(AV=U\Sigma\), con\(V=\left[\begin{array}{r} V_1 \end{array}\right]\), y\(U=\left[\begin{array}{rrr} U_1 & U_2 & U_3 \end{array}\right]\), donde\(U_1\),\(U_2\), y\(U_3\) son las columnas de\(U\). Así\[\begin{aligned} A\left[\begin{array}{r} V_1 \end{array}\right] &= \left[\begin{array}{rrr} U_1 & U_2 & U_3 \end{array}\right]\Sigma\\ \left[\begin{array}{r} AV_1 \end{array}\right] &= \left[\begin{array}{r} \sigma_1 U_1+0U_2+0U_3 \end{array}\right]\\ &= \left[\begin{array}{r} \sigma_1 U_1 \end{array}\right]\end{aligned}\] Esto nos da\(AV_1=\sigma_1 U_1= 3U_1\), por lo\[U_1 = \frac{1}{3}AV_1 = \frac{1}{3} \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right] \left[\begin{array}{r} 1 \end{array}\right] = \frac{1}{3} \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right].\nonumber \]
Los vectores\(U_2\) y\(U_3\) son vectores propios de\(AA^T\) correspondientes al valor propio\(\lambda_2=\lambda_3=0\). En lugar de resolver el sistema\((0I-AA^T)X= 0\) y luego usar el proceso Gram-Schmidt en el conjunto resultante de dos vectores propios básicos, se puede usar el siguiente enfoque.
Encontrar vectores\(U_2\) y\(U_3\) extendiendo primero\(\{ U_1\}\) a una base de\(\mathbb{R}^3\), luego usando el algoritmo Gram-Schmidt para ortogonalizar la base, y finalmente normalizar los vectores.
Empezar con\(\{ 3U_1 \}\) en lugar de\(\{ U_1 \}\) hace la aritmética un poco más fácil. Es fácil verificar que\[\left\{ \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right], \left[\begin{array}{r} 1 \\ 0 \\ 0 \end{array}\right], \left[\begin{array}{r} 0 \\ 1 \\ 0 \end{array}\right]\right\}\nonumber \] es una base de\(\mathbb{R}^3\). Establecer\[E_1 = \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right], X_2 = \left[\begin{array}{r} 1 \\ 0 \\ 0 \end{array}\right], X_3 =\left[\begin{array}{r} 0 \\ 1 \\ 0 \end{array}\right],\nonumber \] y aplicar el algoritmo Gram-Schmidt a\(\{ E_1, X_2, X_3\}\).
Esto nos da\[E_2 = \left[\begin{array}{r} 4 \\ 1 \\ 1 \end{array}\right] \mbox{ and } E_3 = \left[\begin{array}{r} 0 \\ 1 \\ -1 \end{array}\right].\nonumber \]
Por lo tanto,\[U_2 = \frac{1}{\sqrt{18}} \left[\begin{array}{r} 4 \\ 1 \\ 1 \end{array}\right], U_3 = \frac{1}{\sqrt 2} \left[\begin{array}{r} 0 \\ 1 \\ -1 \end{array}\right],\nonumber \] y\[U = \left[\begin{array}{rrr} -\frac{1}{3} & \frac{4}{\sqrt{18}} & 0 \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & \frac{1}{\sqrt 2} \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & -\frac{1}{\sqrt 2} \end{array}\right].\nonumber \]
Por último,\[A = \left[\begin{array}{r} -1 \\ 2 \\ 2 \end{array}\right] = \left[\begin{array}{rrr} -\frac{1}{3} & \frac{4}{\sqrt{18}} & 0 \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & \frac{1}{\sqrt 2} \\ \frac{2}{3} & \frac{1}{\sqrt{18}} & -\frac{1}{\sqrt 2} \end{array}\right] \left[\begin{array}{r} 3 \\ 0 \\ 0 \end{array}\right] \left[\begin{array}{r} 1 \end{array}\right].\nonumber \]
Considera otro ejemplo.
Encontrar una descomposición de valores singulares para la matriz\[A= \left[ \begin{array}{ccc} \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \end{array} \right]\nonumber \]
Solución
Primero considere\(A^TA\)\[\left[ \begin{array}{ccc} \frac{16}{5} & \frac{32}{5} & 0 \\ \frac{32}{5} & \frac{64}{5} & 0 \\ 0 & 0 & 0 \end{array} \right]\nonumber \] ¿Cuáles son algunos autovalores y vectores propios? Algunos programas de computación estos son\[\left\{ \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] ,\left[ \begin{array}{c} -\frac{2}{5}\sqrt{5} \\ \frac{1}{5}\sqrt{5} \\ 0 \end{array} \right] \right\} \leftrightarrow 0,\left\{ \left[ \begin{array}{c} \frac{1}{5}\sqrt{5} \\ \frac{2}{5}\sqrt{5} \\ 0 \end{array} \right] \right\} \leftrightarrow 16\nonumber \] Así la matriz\(V\) viene dada por\[V=\left[ \begin{array}{ccc} \frac{1}{5}\sqrt{5} & -\frac{2}{5}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{5} & \frac{1}{5}\sqrt{5} & 0 \\ 0 & 0 & 1 \end{array} \right]\nonumber \] Siguiente considerar los\(AA^T\)\[\left[ \begin{array}{cc} 8 & 8 \\ 8 & 8 \end{array} \right]\nonumber \] vectores propios y los valores propios son\[\left\{ \left[ \begin{array}{c} -\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} \end{array} \right] \right\} \leftrightarrow 0,\left\{ \left[ \begin{array}{c} \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} \end{array} \right] \right\} \leftrightarrow 16\nonumber \] Así puedes dejar\(U\) que te den\[U=\left[ \begin{array}{cc} \frac{1}{2}\sqrt{2} & -\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{array} \right]\nonumber \] Vamos a verificar esto. \(U^TAV=\)\[\left[ \begin{array}{cc} \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{array} \right] \left[ \begin{array}{ccc} \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{2}\sqrt{5} & \frac{4}{5}\sqrt{2}\sqrt{5} & 0 \end{array} \right] \left[ \begin{array}{ccc} \frac{1}{5}\sqrt{5} & -\frac{2}{5}\sqrt{5} & 0 \\ \frac{2}{5}\sqrt{5} & \frac{1}{5}\sqrt{5} & 0 \\ 0 & 0 & 1 \end{array} \right]\nonumber \]\[=\left[ \begin{array}{ccc} 4 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right]\nonumber \]
Esto ilustra que si tienes una buena manera de encontrar los vectores propios y los valores propios para una matriz hermitiana que tiene valores propios no negativos, entonces también tienes una buena manera de encontrar la descomposición de valores singulares de una matriz arbitraria.
Matrices Definitivas Positivas
Las matrices definidas positivas a menudo se encuentran en aplicaciones tales como mecánicas y estadísticas.
Comenzamos con una definición.
Dejar\(A\) ser una matriz\(n \times n\) simétrica. Entonces\(A\) es positivo definido si todos sus valores propios son positivos.
La relación entre una matriz definida negativa y una matriz definida positiva es la siguiente.
Una\(n\times n\) matriz\(A\) es negativa definida si y solo si\(-A\) es positiva definida
Considera el siguiente lema.
Si\(A\) es positivo definido, entonces es invertible.
- Prueba
-
Si\(A\vec{v}=\vec{0},\) entonces\(0\) es un valor propio si\(\vec{v}\) es distinto de cero, lo que no sucede para una matriz definida positiva. De ahí\(\vec{v}=\vec{0}\) y así\(A\) es uno a uno. Esto es suficiente para concluir que es invertible.
Observe que este lema implica que si una matriz\(A\) es positiva definitiva, entonces\(\det(A) > 0\).
El siguiente teorema proporciona otra caracterización de matrices definidas positivas. Da una prueba útil para verificar si una matriz es positiva definitiva.
Dejar\(A\) ser una matriz simétrica. Entonces\(A\) es positivo definido si y solo si\(\vec{x}^T A \vec{x}\) es positivo para todos los distintos de cero\(\vec{x} \in \mathbb{R}^n\).
- Prueba
-
Dado que\(A\) es simétrico, existe una matriz ortogonal de\(U\) manera que\[U^{T}AU=diag(\lambda_1,\lambda_2,\ldots,\lambda_n)=D,\nonumber \] donde\(\lambda_1,\lambda_2,\ldots,\lambda_n\) están los valores propios (no necesariamente distintos) de\(A\). Dejar\(\vec{x}\in\mathbb{R}^n\),\(\vec{x}\neq \vec{0}\), y definir\(\vec{y}=U^T\vec{x}\). Entonces\[\vec{x}^TA\vec{x}=\vec{x}^T(UDU^T)\vec{x} = (\vec{x}^TU)D(U^T\vec{x}) =\vec{y}^TD\vec{y}.\nonumber \]
Redacción\(\vec{y}^T=\left[\begin{array}{cccc} y_1 & y_2 & \cdots & y_n\end{array}\right]\),\[\begin{aligned} \vec{x}^TA\vec{x} & = \left[\begin{array}{cccc} y_1 & y_2 & \cdots & y_n\end{array}\right] diag(\lambda_1,\lambda_2,\ldots,\lambda_n) \left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n\end{array}\right]\\ & = \lambda_1 y_1^2 + \lambda_2 y_2^2 + \cdots \lambda_n y_n^2.\end{aligned}\]
\((\Rightarrow)\)Primero asumiremos que\(A\) es positivo definido y demostraremos que\(\vec{x}^T A \vec{x}\) es positivo.
Supongamos que\(A\) es positivo definido, y\(\vec{x}\in\mathbb{R}^n\),\(\vec{x}\neq\vec{0}\). Ya que\(U^T\) es invertible\(\vec{y}=U^T\vec{x}\neq \vec{0}\),, y así\(y_j\neq 0\) para algunos\(j\), implicando\(y_j^2>0\) para algunos\(j\). Además, ya que todos los valores propios de\(A\) son positivos,\(\lambda_i y_i^2\geq 0\) para todos\(i\) y\(\lambda_jy_j^2>0\). Por lo tanto,\(\vec{x}^TA\vec{x}>0\).
\((\Leftarrow)\)Ahora vamos a suponer que\(\vec{x}^T A \vec{x}\) es positivo y demostraremos que\(A\) es positivo definitivo.
Si\(\vec{x}^TA\vec{x}>0\) cuando sea\(\vec{x}\neq \vec{0}\), elija\(\vec{x}=U\vec{e}_j\), donde\(\vec{e}_j\) esta la\(j^{\mbox{th}}\) columna de\(I_n\). Ya que\(U\) es invertible,\(\vec{x}\neq\vec{0}\), y por lo\[\vec{y}=U^T\vec{x}=U^T(U\vec{e}_j) =\vec{e}_j.\nonumber \] tanto Así\(y_j=1\) y\(y_i=0\) cuándo\(i\neq j\), así\[\lambda_1 y_1^2 + \lambda_2 y_2^2 + \cdots \lambda_n y_n^2 =\lambda_j,\nonumber \] es decir,\(\lambda_j=\vec{x}^TA\vec{x}>0\). Por lo tanto,\(A\) es positivo definido.
Hay algunas otras consecuencias muy interesantes que resultan de que una matriz sea positiva y definitiva. Primero se puede observar que la propiedad de ser positivo definido se transfiere a cada una de las submatrices principales que ahora definiremos.
\(A\)Déjese ser una\(n\times n\) matriz. Denote por\(A_{k}\) la\(k\times k\) matriz obtenida al eliminar las\(k+1,\cdots ,n\) columnas y las\(k+1,\cdots ,n\) filas de\(A.\) Así\(A_{n}=A\) y\(A_{k}\) es la\(k\times k\) submatriz de la\(A\) cual ocupa la esquina superior izquierda de\(A.\)
Dejar\(A\) ser una matriz definitiva\(n\times n\) positiva. Entonces cada submatriz también\(A_{k}\) es positiva definida.
- Prueba
-
Esto se desprende enseguida de la definición anterior. Dejemos\(\vec{x}\in \mathbb{R}^{k}\) ser distinto de cero. Entonces\[\vec{x}^{T}A_{k}\vec{x}=\left[ \begin{array}{cc} \vec{x}^{T} & 0 \end{array} \right] A\left[ \begin{array}{c} \vec{x} \\ 0 \end{array} \right] > 0\nonumber \] por la suposición que\(A\) es positiva definitiva.
Hay otra manera de reconocer si una matriz es positiva definida que se describe en términos de estas submatrices. Declaramos el resultado, cuya prueba se puede encontrar en textos más avanzados.
Dejar\(A\) ser una matriz simétrica. Entonces\(A\) es positivo definido si y sólo si\(\det \left( A_{k}\right)\) es mayor que\(0\) para cada submatriz\(A_{k}\),\(k=1,\cdots ,n\).
- Prueba
-
Demostramos este teorema por inducción sobre\(n.\) Es claramente cierto si\(n=1.\) Supongamos entonces que es cierto para\(n-1\) dónde\(n\geq 2\). Ya\(\det \left( A\right) =\det \left( A_{n}\right) >0,\) que se deduce que todos los valores propios son distintos de cero. Tenemos que demostrar que todos son positivos. Supongamos que no. Entonces hay algún número par de ellos que son negativos, incluso porque se sabe que el producto de todos los valores propios es positivo, igualando\(\det \left( A\right)\). Escoge dos,\(\lambda _{1}\)\(\lambda _{2}\) y deja\(A \vec{u}_{i}=\lambda _{i}\vec{u}_{i}\) donde\(\vec{u}_{i}\neq \vec{0}\) para\(i=1,2\) y\(\vec{u}_{1}\cdot \vec{u}_{2}=0.\) ahora si\(\vec{y}\equiv \alpha _{1}\vec{u}_{1}+\alpha _{2}\vec{u}_{2}\) es un elemento de\(span\left\{ \vec{u}_{1},\vec{u}_{2}\right\} ,\) entonces ya que estos son valores propios y\(\ \vec{u}_{1}\cdot \vec{u}_{2}=0,\) un breve cálculo muestra\[\left( \alpha _{1}\vec{u}_{1}+\alpha _{2}\vec{u}_{2}\right) ^{T}A\left( \alpha _{1}\vec{u}_{1}+\alpha _{2}\vec{u}_{2}\right)\nonumber \]\[=\left\vert \alpha _{1}\right\vert ^{2}\lambda _{1} \vec{u} _{1} ^{2}+\left\vert \alpha _{2}\right\vert ^{2}\lambda _{2}\vec{u}_{2}^{2}<0.\nonumber \] ahora dejando que\(\vec{x}\in \mathbb{R}^{n-1},\) podamos usar la inducción hipótesis para escribir\[\left[ \begin{array}{cc} x^{T} & 0 \end{array} \right] A\left[ \begin{array}{c} \vec{x} \\ 0 \end{array} \right] =\vec{x}^{T}A_{n-1}\vec{x}>0.\nonumber \] Ahora la dimensión de\(\left\{ \vec{z}\in \mathbb{R}^{n}:z_{n}=0\right\}\) es\(n-1\) y la dimensión de\(span\left\{ \vec{u}_{1},\vec{u} _{2}\right\} =2\) y así debe haber algún distinto de cero\(\vec{x}\in \mathbb{R} ^{n}\) que esté en ambos de estos subespacios de\(\mathbb{R}^{n}\). No obstante, el primer cómputo requeriría que\(\vec{x}^{T}A\vec{x}<0\) mientras que el segundo requeriría que\(\vec{x}^{T}A\vec{x}>0.\) esta contradicción demuestre que todos los valores propios deben ser positivos. Esto prueba la parte if del teorema. También se puede demostrar que lo contrario es correcto, pero es la dirección que se acaba de mostrar la que es de mayor interés.
Que\(A\) sean simétricos. Entonces\(A\) es negativo definitivo si y sólo si\[\left( -1\right) ^{k} \det \left( A_{k}\right) >0\nonumber \] por cada\(k=1,\cdots ,n\).
- Prueba
-
Esto es inmediato del teorema anterior cuando notamos, eso\(A\) es negativo definido si y sólo si\(-A\) es positivo definido. Por lo tanto, si\(\det \left( -A_{k}\right) >0\) por todos\(k=1,\cdots ,n,\) se deduce que\(A\) es negativo definitivo. Sin embargo,\(\det \left( -A_{k}\right) =\left( -1\right) ^{k}\det \left( A_{k}\right) .\)
La factorización de Cholesky
Otro teorema importante es la existencia de una factorización específica de matrices definidas positivas. Se llama Factorización Cholesky y factoriza la matriz en el producto de una matriz triangular superior y su transposición.
\(A\)Sea una matriz definitiva positiva. Entonces existe una matriz triangular superior\(U\) cuyas entradas diagonales principales son positivas, tal que se\(A\) puede escribir\[A= U^TU\nonumber \] Esta factorización es única.
El proceso para encontrar una matriz de este tipo\(U\) se basa en operaciones simples de fila.
\(A\)Sea una matriz definitiva positiva. La matriz\(U\) que crea la Factorización Cholesky se puede encontrar a través de dos pasos.
- Usando solo tipo operaciones de fila\(3\) elemental (múltiplos de filas agregadas a otras filas) poner\(A\) en forma triangular superior. Llama a esta matriz\(\hat{U}\). Después\(\hat{U}\) tiene entradas positivas en la diagonal principal.
- Divida cada fila de\(\hat{U}\) por la raíz cuadrada de la entrada diagonal en esa fila. El resultado es la matriz\(U\).
Por supuesto siempre puedes verificar que tu factorización es correcta multiplicando\(U\) y\(U^T\) para asegurar que el resultado sea la matriz original\(A\).
Considera el siguiente ejemplo.
Demostrar que\(A=\left[\begin{array}{rrr} 9 & -6 & 3 \\ -6 & 5 & -3 \\ 3 & -3 & 6 \end{array}\right]\) es positivo definitivo, y encontrar la factorización Cholesky de\(A\).
Solución
Primero demostramos que\(A\) es positivo definido. Por Teorema\(\PageIndex{8}\) basta con mostrar que el determinante de cada submatriz es positivo. \[A_{1}=\left[\begin{array}{c} 9 \end{array}\right] \mbox{ and } A_{2}=\left[\begin{array}{rr} 9 & -6 \\ -6 & 5 \end{array}\right],\nonumber \]así\(\det(A_{1})=9\) y\(\det(A_{2})=9\). Ya que\(\det(A)=36\), de ello se deduce que\(A\) es positivo definitivo.
Ahora usamos Procedimiento\(\PageIndex{1}\) para encontrar la Factorización Cholesky. Reducción de filas (usando solo operaciones de\(3\) fila tipo) hasta obtener una matriz triangular superior. \[\left[\begin{array}{rrr} 9 & -6 & 3 \\ -6 & 5 & -3 \\ 3 & -3 & 6 \end{array}\right] \rightarrow \left[\begin{array}{rrr} 9 & -6 & 3 \\ 0 & 1 & -1 \\ 0 & -1 & 5 \end{array}\right] \rightarrow \left[\begin{array}{rrr} 9 & -6 & 3 \\ 0 & 1 & -1 \\ 0 & 0 & 4 \end{array}\right]\nonumber \]
Ahora divide las entradas en cada fila por la raíz cuadrada de la entrada diagonal en esa fila, para dar\[U=\left[\begin{array}{rrr} 3 & -2 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 2 \end{array}\right]\nonumber \]
Eso se puede verificar\(U^TU = A\).
Dejar\(A\) ser una matriz definitiva positiva dada por\[\left[ \begin{array}{ccc} 3 & 1 & 1 \\ 1 & 4 & 2 \\ 1 & 2 & 5 \end{array} \right]\nonumber \] Determinar su factorización Cholesky.
Solución
Se puede verificar que de hecho\(A\) es positivo definitivo.
Para encontrar la factorización de Cholesky primero la fila reducimos a una matriz triangular superior. \[\left[ \begin{array}{ccc} 3 & 1 & 1 \\ 1 & 4 & 2 \\ 1 & 2 & 5 \end{array} \right] \rightarrow \left[ \begin{array}{ccc} 3 & 1 & 1 \\ 0 & \frac{11}{3} & \frac{5}{3} \\ 0 & \frac{5}{3} & \frac{14}{5} \end{array} \right] \rightarrow \left[ \begin{array}{ccc} 3 & 1 & 1 \\ 0 & \frac{11}{3} & \frac{5}{3} \\ 0 & 0 & \frac{43}{11} \end{array} \right]\nonumber \]
Ahora divida las entradas en cada fila por la raíz cuadrada de la entrada diagonal en esa fila y simplifique. \[U = \left[ \begin{array}{ccc} \sqrt{3} & \frac{1}{3}\sqrt{3} & \frac{1}{3}\sqrt{3} \\ 0 & \frac{1}{3}\sqrt{3}\sqrt{11} & \frac{5}{33}\sqrt{3}\sqrt{11} \\ 0 & 0 & \frac{1}{11}\sqrt{11}\sqrt{43} \end{array} \right]\nonumber \]
Factorización QR
En esta sección se estudia una factorización confiable de matrices. Llamada la\(QR\) factorización de una matriz, siempre existe. Si bien se puede decir mucho sobre la\(QR\) factorización, esta sección se limitará a matrices reales. Por lo tanto, asumimos que el producto punto utilizado a continuación es el producto punto habitual. Comenzamos con una definición.
\(A\)Déjese ser una\(m\times n\) matriz real. Entonces una\(QR\) factorización de\(A\) consiste en dos matrices,\(Q\) ortogonales y triangulares\(R\) superiores, de tal manera que\(A=QR.\)
qrfactorización
El siguiente teorema afirma que tal factorización existe.
Dejar\(A\) ser cualquier\(m\times n\) matriz real con columnas linealmente independientes. Luego existe una matriz ortogonal\(Q\) y una matriz triangular superior\(R\) que tiene entradas no negativas en la diagonal principal de tal manera que\[A=QR\nonumber\]
El procedimiento para obtener la\(QR\) factorización para cualquier matriz\(A\) es el siguiente.
Dejar\(A\) ser una\(m \times n\) matriz dada por\(A = \left[ \begin{array}{cccc} A_1 & A_2 & \cdots & A_n \end{array} \right]\) donde las\(A_i\) son las columnas linealmente independientes de\(A\).
- Aplicar el Proceso Gram-Schmidt 4.11.1 a las columnas de\(A\), escribiendo\(B_i\) para las columnas resultantes.
- Normalizar el\(B_i\), para encontrar\(C_i = \frac{1}{ B_i } B_i\).
- Construir la matriz ortogonal\(Q\) como\(Q=\left[ \begin{array}{cccc} C_1 & C_2 & \cdots & C_n \end{array} \right]\).
- Construir la matriz triangular superior\(R\) como\[R = \left[ \begin{array}{ccccc} B_1 & A_2 \cdot C_1 & A_3 \cdot C_1 & \cdots & A_n \cdot C_1 \\ 0 & B_2 & A_3 \cdot C_2 & \cdots & A_n \cdot C_2 \\ 0 & 0 & B_3 & \cdots & A_n \cdot C_3 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & B_n \end{array} \right]\nonumber \]
- Finalmente, escribe\(A=QR\) donde\(Q\) está la matriz ortogonal y\(R\) es la matriz triangular superior obtenida anteriormente.
Observe que\(Q\) es una matriz ortogonal como la\(C_i\) forma un conjunto ortonormal. Ya que\( B_i > 0\) para todos\(i\) (ya que la longitud de un vector es siempre positiva), se deduce que\(R\) es una matriz triangular superior con entradas positivas en la diagonal principal.
Considera el siguiente ejemplo.
Vamos\[A = \left[ \begin{array}{rr} 1 & 2 \\ 0 & 1 \\ 1 & 0 \end{array} \right]\nonumber \] Encuentra una matriz ortogonal\(Q\) y una matriz triangular superior\(R\) tal que\(A=QR\).
Solución
Primero, observar que\(A_1\),\(A_2\), las columnas de\(A\), son linealmente independientes. Por lo tanto, podemos usar el Proceso Gram-Schmidt para crear un conjunto ortogonal correspondiente de la\(\left\{ B_1, B_2 \right\}\) siguiente manera:\[\begin{aligned} B_1 &= A_1 = \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] \\ B_2 &= A_2 - \frac{A_2 \cdot B_1}{ B_1 ^2} B_1 \\ &= \left[ \begin{array}{r} 2 \\ 1 \\ 0 \end{array} \right] - \frac{2}{2} \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \right]\end{aligned}\]
Normaliza cada vector para crear el conjunto de la\(\left\{ C_1, C_2 \right\}\) siguiente manera:\[\begin{aligned} C_1 &= \frac{1}{ B_1 } B_1 = \frac{1}{\sqrt{2}} \left[ \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right] \\ C_2 &= \frac{1}{ B_2 } B_2 = \frac{1}{\sqrt{3}} \left[ \begin{array}{r} 1 \\ 1 \\ -1 \end{array}\right]\end{aligned}\]
Ahora construye la matriz ortogonal\(Q\) como\[\begin{aligned} Q &= \left[ \begin{array}{cccc} C_1 & C_2 & \cdots & C_n \end{array} \right] \\ &= \left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ 0 & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{2}} & - \frac{1}{\sqrt{3}} \end{array} \right]\end{aligned}\]
Finalmente, construir la matriz triangular superior\(R\) como\[\begin{aligned} R &= \left[ \begin{array}{cc} B_1 & A_2 \cdot C_1 \\ 0 & B_2 \end{array} \right] \\ &= \left[ \begin{array}{cc} \sqrt{2} & \sqrt{2} \\ 0 & \sqrt{3} \\ \end{array} \right]\end{aligned}\]
Se deja al lector verificar eso\(A=QR\).
La\(QR\) factorización y los valores propios
La\(QR\) factorización de una matriz tiene una aplicación muy útil. Resulta que se puede utilizar repetidamente para estimar los valores propios de una matriz. Considera el siguiente procedimiento.
Dejar\(A\) ser una matriz invertible. Defina las matrices de\(A_1, A_2, \cdots\) la siguiente manera:
- \(A_1 = A\)factorizado como\(A_1 = Q_1R_1\)
- \(A_2 = R_1Q_1\)factorizado como\(A_2 = Q_2R_2\)
- \(A_3 = R_2Q_2\)factorizado como\(A_3 = Q_3R_3\)
Continuar de esta manera, donde en general\(A_k = Q_kR_k\) y\(A_{k+1} = R_kQ_k\).
Entonces se deduce que esta secuencia de\(A_i\) converge a una matriz triangular superior que es similar a\(A\). Por lo tanto, los valores propios de\(A\) pueden ser aproximados por las entradas en la diagonal principal de esta matriz triangular superior.
Métodos de Poder
Si bien el\(QR\) algoritmo se puede usar para calcular valores propios, existe una técnica útil y bastante elemental para encontrar el autovector y el valor propio asociado más cercano a un número complejo dado que se llama el método de potencia inversa desplazada. Tiende a funcionar extremadamente bien siempre que comiences con algo que esté bastante cerca de un valor propio.
Los métodos de poder se basan en la consideración de poderes de una matriz dada. Dejar\(\left\{ \vec{x}_{1},\cdots ,\vec{x}_{n}\right\}\) ser una base de vectores propios para\(\mathbb{C}^{n}\) tal que\(A\vec{x}_{n}=\lambda _{n}\vec{x}_{n}.\) Ahora vamos a\(\vec{u}_{1}\) ser algún vector distinto de cero. Ya que\(\left\{ \vec{x}_{1},\cdots ,\vec{x}_{n}\right\}\) es una base, existen escalares únicos,\(c_{i}\) tales que\[\vec{u}_{1}=\sum_{k=1}^{n}c_{k}\vec{x}_{k}\nonumber \] Supongamos que no has sido tan desafortunado como para escoger de tal\(\vec{u}_{1}\) manera que\(c_{n}=0.\)\(A\vec{u}_{k}=\vec{u}_{k+1}\) Entonces deja\[\vec{u}_{m}=A^{m}\vec{u}_{1}=\sum_{k=1}^{n-1}c_{k}\lambda _{k}^{m}\vec{x} _{k}+\lambda _{n}^{m}c_{n}\vec{x}_{n}. \label{20maye1}\] para que Para grandes\(m\) el último término,\(\lambda _{n}^{m}c_{n}\vec{x}_{n},\) determina bastante bien la dirección del vector a la derecha. Esto se debe a que\(\left\vert \lambda _{n}\right\vert\) es mayor que\(\left\vert \lambda _{k}\right\vert\) para\(k<n\) y así para un grande\(m,\) la suma,\(\sum_{k=1}^{n-1}c_{k}\lambda _{k}^{m}\vec{x}_{k},\) a la derecha es bastante insignificante. Por lo tanto, para grandes\(m,\)\(\vec{u}_{m}\) es esencialmente un múltiplo del vector propio\(\vec{x}_{n},\) el que va con\(\lambda _{n}.\) El único problema es que no hay control del tamaño de los vectores\(\vec{u}_{m}.\) Puedes arreglar esto escalando. Dejar\(S_{2}\) denotar la entrada de la\(A\vec{u}_{1}\) cual es mayor en valor absoluto. A esto lo llamamos factor de escalamiento. Entonces no\(\vec{u}_{2}\) será solo\(A\vec{u}_{1}\) sino\(A\vec{u}_{1}/S_{2}.\) Siguiente vamos a\(S_{3}\) denotar la entrada de la\(A\vec{u}_{2}\) cual tiene mayor valor absoluto y definir\(\vec{u}_{3}\equiv A\vec{u}_{2}/S_{3}.\) Continuar de esta manera. El escalado que se acaba de describir no destruye la relativa insignificancia del término que implica una suma en\(\eqref{20maye1}\). Efectivamente no equivale más que cambiar las unidades de longitud. También tenga en cuenta que a partir de este procedimiento de escalado, el valor absoluto del elemento más grande de siempre\(\vec{u}_{k}\) es igual a 1. Por lo tanto, para grandes\(m,\)\[\vec{u}_{m}= \frac{\lambda _{n}^{m}c_{n}\vec{x}_{n}}{S_{2}S_{3}\cdots S_{m}}+\left( \text{relatively insignificant term}\right) .\nonumber \] Por lo tanto, la entrada de la\(A\vec{u}_{m}\) cual tiene el mayor valor absoluto es esencialmente igual a la entrada que tiene mayor valor absoluto de\[A\left( \frac{\lambda _{n}^{m}c_{n}\vec{x}_{n}}{S_{2}S_{3}\cdots S_{m}}\right) = \frac{\lambda _{n}^{m+1}c_{n} \vec{x}_{n}}{S_{2}S_{3}\cdots S_{m}}\approx \lambda _{n}\vec{u}_{m}\nonumber \] y así para grande debe\(m,\) darse el caso que\(\lambda _{n}\approx S_{m+1}.\) Esto sugiere el siguiente procedimiento.
- Comienza con un vector\(\vec{u}_{1}\) que esperas que tenga un componente en la dirección de\(\vec{x}_{n}.\) El vector\(\left( 1,\cdots ,1\right) ^{T}\) suele ser una opción bastante buena.
- Si\(\vec{u}_{k}\) se conoce,\[\vec{u}_{k+1}=\frac{A\vec{u}_{k}}{S_{k+1}}\nonumber \] dónde\(S_{k+1}\) está la entrada de la\(A\vec{u}_{k}\) cual tiene mayor valor absoluto.
- Cuando los factores de escalado, no\(S_{k}\) están cambiando mucho,\(S_{k+1}\) estarán cerca del valor propio y\(\vec{u}_{k+1}\) estarán cerca de un vector propio.
- Consulta tu respuesta para ver si funcionó bien.
El método de potencia inversa desplazada implica encontrar el valor propio más cercano a un número complejo dado junto con el valor propio asociado. Si\(\mu\) es un número complejo y desea encontrar\(\lambda\) cuál es el más cercano a\(\mu ,\) usted podría considerar los valores propios y los vectores propios de\(\left( A-\mu I\right) ^{-1}\). Entonces\(A\vec{x}=\lambda \vec{x}\) si y solo si\[\left( A-\mu I\right) \vec{x}=\left( \lambda -\mu \right) \vec{x}\nonumber \] Si y solo si\[\frac{1}{\lambda -\mu }\vec{x}=\left( A-\mu I\right) ^{-1}\vec{x}\nonumber \] Así, si\(\lambda\) es el valor propio más cercano de\(A\) a\(\mu\) entonces de todos los valores propios de\(\left( A-\mu I\right) ^{-1},\) ustedes\(\frac{1}{ \lambda -\mu }\) tendría sería el mayor. Así, todo lo que tienes que hacer es aplicar el método power\(\left( A-\mu I\right) ^{-1}\) y el autovector que obtengas será el vector propio que corresponde a\(\lambda\) donde\(\lambda\) está el más cercano a\(\mu\) de todos los autovalores de\(A\). Podría usar el vector propio para determinar esto directamente.
Encuentra el valor propio y el vector propio para el\[\left[ \begin{array}{rrr} 3 & 2 & 1 \\ -2 & 0 & -1 \\ -2 & -2 & 0 \end{array} \right]\nonumber \] que está más cerca\(.9+.9i\).
Solución
\[\left ( \left[ \begin{array}{rrr} 3 & 2 & 1 \\ -2 & 0 & -1 \\ -2 & -2 & 0 \end{array} \right] - (.9+.9i)\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] \right )^{-1}\nonumber \]
\[= \left[ \begin{array}{ccc} -0.619\,19-10.\, 545i & -5.\, 524\,9-4.\, 972\,4i & -0.370\,57-5.\, 821\,3i \\ 5.\, 524\,9+4.\, 972\,4i & 5.\, 276\,2+0.248\,62i & 2.\, 762\,4+2.\, 486\,2i \\ 0.741\,14+11.\, 643i & 5.\, 524\,9+4.\, 972\,4i & 0.492\,52+6.\, 918\,9i \end{array} \right]\nonumber \]
Entonces escoge una conjetura inicial y multiplicar por esta matriz elevada a una gran potencia. \[= \left[ \begin{array}{ccc} -0.619\,19-10.\, 545i & -5.\, 524\,9-4.\, 972\,4i & -0.370\,57-5.\, 821\,3i \\ 5.\, 524\,9+4.\, 972\,4i & 5.\, 276\,2+0.248\,62i & 2.\, 762\,4+2.\, 486\,2i \\ 0.741\,14+11.\, 643i & 5.\, 524\,9+4.\, 972\,4i & 0.492\,52+6.\, 918\,9i \end{array} \right]^{15}\left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right]\nonumber \]
Esto es igual a\[\left[ \begin{array}{c} 1.\, 562\,9\times 10^{13}-3.\, 899\,3\times 10^{12}i \\ -5.\, 864\,5\times 10^{12}+9.\, 764\,2\times 10^{12}i \\ -1.\, 562\,9\times 10^{13}+3.\, 899\,9\times 10^{12}i \end{array} \right]\nonumber \] Ahora divide por una entrada para hacer que el vector tenga un tamaño razonable. Esto rinde\[\left[ \begin{array}{c} -0.999\,99-3.\, 614\,0\times 10^{-5}i \\ 0.499\,99-0.499\,99i \\ 1.0 \end{array} \right]\nonumber\] lo que está cerca de\[\left[ \begin{array}{c} -1 \\ 0.5-0.5i \\ 1.0 \end{array} \right]\nonumber\] Entonces\[\left[ \begin{array}{rrr} 3 & 2 & 1 \\ -2 & 0 & -1 \\ -2 & -2 & 0 \end{array} \right] \left[ \begin{array}{c} -1 \\ 0.5-0.5i \\ 1.0 \end{array} \right] =\left[ \begin{array}{c} -1.0-1.0i \\ 1.0 \\ 1.0+1.0i \end{array} \right]\nonumber \] Ahora para determinar el valor propio, se podría simplemente tomar la relación de entradas correspondientes. Elija las dos entradas correspondientes que tengan los valores absolutos más grandes. En este caso, se obtendría el valor propio es el\(1+i\) que pasa a ser el valor propio exacto. Por lo tanto, un vector propio y un valor propio son\[\left[ \begin{array}{c} -1 \\ 0.5-0.5i \\ 1.0 \end{array} \right], 1+i\nonumber \]
Por lo general no va a funcionar tan bien pero aún puedes encontrar lo que se desea. Por lo tanto, una vez que haya obtenido valores propios aproximados usando el\(QR\) algoritmo, puede encontrar el valor propio más exactamente junto con un vector propio asociado con él utilizando el método de potencia inversa desplazada.
Formas cuadráticas
Una de las aplicaciones de la diagonalización ortogonal es la de formas cuadráticas y gráficas de curvas de nivel de una forma cuadrática. Esta sección tiene que ver con la rotación de ejes para que con respecto a los nuevos ejes, la gráfica de la curva de nivel de una forma cuadrática se oriente paralela a los ejes de coordenadas. Esto hace que sea mucho más fácil de entender. Por ejemplo, todos sabemos que\(x_1^2 + x_2^2=1\) representa la ecuación en dos variables cuya gráfica en\(\mathbb{R}^2\) es un círculo de radio\(1\). Pero, ¿cómo sabemos lo que\(5x_1^2 + 4x_1x_2 + 3x_2^2=1\) representa la gráfica de la ecuación?
Primero definimos formalmente lo que se entiende por una forma cuadrática. En esta sección trabajaremos únicamente con formas cuadráticas reales, lo que significa que los coeficientes serán todos números reales.
Una forma cuadrática es un polinomio de grado dos en\(n\) variables\(x_1, x_2, \cdots, x_n\), escrito como una combinación lineal de\(x_i^{2}\) términos y\(x_ix_j\) términos.
Considera la forma cuadrática\(q = a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + a_{12}x_1x_2 + \cdots\). Podemos escribir\(\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right]\) como el vector cuyas entradas son las variables contenidas en la forma cuadrática.
Del mismo modo, deja\(A = \left[ \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right]\) ser la matriz cuyas entradas son los coeficientes de\(x_i^2\) y\(x_ix_j\) de\(q\). Tenga en cuenta que la matriz no\(A\) es única, y consideraremos esto más a fondo en el siguiente ejemplo. Usando esta matriz\(A\), la forma cuadrática se puede escribir como\(q = \vec{x}^T A \vec{x}\).
\[\begin{aligned} q &= \vec{x}^T A \vec{x} \\ &= \left[ \begin{array}{rrrr} x_1 & x_2 & \cdots & x_n \end{array} \right] \left[ \begin{array}{rrrr} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right] \left[ \begin{array}{r} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right] \\ &= \left[ \begin{array}{rrrr} x_1 & x_2 & \cdots & x_n \end{array} \right] \left[ \begin{array}{c} a_{11}x_1 + a_{21}x_2 + \cdots + a_{n1}x_n \\ a_{12}x_1 + a_{22}x_2 + \cdots + a_{n2}x_n \\ \vdots \\ a_{1n}x_1 + a_{2n}x_2 + \cdots + a_{nn}x_n \end{array} \right] \\ &= a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + a_{12}x_1x_2 + \cdots\end{aligned}\]
Exploremos cómo encontrar esta matriz\(A\). Considera el siguiente ejemplo.
Deja que una forma cuadrática\(q\) sea dada por\[q = 6x_1^2 + 4x_1x_2 + 3x_2^2\nonumber \] Escribe\(q\) en el formulario\(\vec{x}^TA\vec{x}\).
Solución
Primero, vamos\(\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right]\) y\(A = \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]\).
Entonces, la escritura\(q = \vec{x}^TA\vec{x}\) da\[\begin{aligned} q &= \left[ \begin{array}{rr} x_1 & x_2 \end{array} \right] \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right] \\ &= a_{11}x_1^2 + a_{21}x_1x_2 + a_{12}x_1x_2 + a_{22}x_2^2\end{aligned}\]
Observe que tenemos un\(x_1x_2\) término así como un\(x_2x_1\) término. Dado que la multiplicación es conmutativa, estos términos se pueden combinar. Esto significa que\(q\) se puede escribir\[q = a_{11}x_1^2 + \left( a_{21}+ a_{12}\right) x_1x_2 + a_{22}x_2^2\nonumber \]
Equiparando esto a\(q\) como se da en el ejemplo, tenemos\[a_{11}x_1^2 + \left( a_{21}+ a_{12}\right) x_1x_2 + a_{22}x_2^2 = 6x_1^2 + 4x_1x_2 + 3x_2^2\nonumber \]
Por lo tanto,\[\begin{aligned} a_{11} &= 6 \\ a_{22} &= 3 \\ a_{21}+a_{12} &= 4\end{aligned}\]
Esto demuestra que la matriz no\(A\) es única, ya que existen varias soluciones correctas para\(a_{21}+a_{12} = 4\). No obstante, siempre elegiremos los coeficientes de tal manera que\(a_{21} = a_{12} = \frac{1}{2} (a_{21}+a_{12})\). Esto da como resultado\(a_{21} = a_{12} = 2\). Esta elección es clave, ya que asegurará que\(A\) resulte ser una matriz simétrica.
De ahí que,\[A = \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] = \left[ \begin{array}{rr} 6 & 2 \\ 2 & 3 \end{array} \right]\nonumber \]
Puede verificar que se\(q = \vec{x}^T A \vec{x}\) detenga para esta elección de\(A\).
El procedimiento anterior\(A\) para elegir ser simétrico aplica para cualquier forma cuadrática\(q\). Siempre elegiremos coeficientes tales que\(a_{ij}=a_{ji}\).
Pasamos ahora nuestra atención al foco de esta sección. Nuestro objetivo es comenzar con una forma cuadrática\(q\) como la dada anteriormente y encontrar la manera de reescribirla para eliminar los\(x_ix_j\) términos. Esto se hace a través de un cambio de variables. En otras palabras, deseamos encontrar\(y_i\) tal que\[q = d_{11}y_1^2 + d_{22}y_2^2 + \cdots + d_{nn}y_n^2\nonumber \] Letting\(\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]\) y\(D = \left[ d_{ij} \right]\), podemos escribir de\(q = \vec{y}^T D \vec{y}\) dónde\(D\) está la matriz de coeficientes de\(q\). Hay algo especial en esta matriz\(D\) que es crucial. Como no existen\(y_iy_j\) términos en\(q\), se deduce que\(d_{ij} = 0\) para todos\(i \neq j\). Por lo tanto,\(D\) es una matriz diagonal. A través de este cambio de variables, encontramos los ejes principales\(y_1, y_2, \cdots, y_n\) de la forma cuadrática.
Esta discusión sienta las bases para el siguiente teorema esencial.
Dejar\(q\) ser una forma cuadrática en las variables\(x_1, \cdots, x_n\). De ello se deduce que se\(q\) puede escribir en la forma\(q = \vec{x}^T A \vec{x}\) donde\[\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right]\nonumber \] y\(A = \left[ a_{ij} \right]\) es la matriz simétrica de coeficientes de\(q\).
Se\(y_1, y_2, \cdots, y_n\) pueden encontrar nuevas variables tales que\(q = \vec{y}^T D \vec{y}\) donde\[\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]\nonumber \] y\(D=\left[ d_{ij} \right]\) es una matriz diagonal. La matriz\(D\) contiene los valores propios de\(A\) y se encuentra diagonalizando ortogonalmente\(A\).
Si bien no es una prueba formal, la siguiente discusión debería convencerte de que el teorema anterior sostiene. Dejar\(q\) ser una forma cuadrática en las variables\(x_1, \cdots, x_n\). Entonces, se\(q\) puede escribir en la forma\(q = \vec{x}^T A \vec{x}\) para una matriz simétrica\(A\). Por Teorema\(\PageIndex{3}\) podemos diagonalizar ortogonalmente la matriz\(A\) tal que\(U^TAU = D\) para una matriz ortogonal\(U\) y una matriz diagonal\(D\).
Entonces, el vector\(\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]\) es encontrado por\(\vec{y} = U^T \vec{x}\). Para ver que esto funciona, reescribe\(\vec{y} = U^T \vec{x}\) como\(\vec{x} = U\vec{y}\). Dejando\(q = \vec{x}^TA\vec{x}\), proceder de la siguiente manera:\[\begin{aligned} q &= \vec{x}^T A \vec{x}\\ &= (U\vec{y})^T A (U\vec{y})\\ &= \vec{y}^T (U^TAU) \vec{y} \\ &= \vec{y}^T D \vec{y}\end{aligned}\]
El siguiente procedimiento detalla los pasos para el cambio de variables dados en el teorema anterior.
Dejar\(q\) ser una forma cuadrática en las variables\(x_1, \cdots, x_n\) dadas por\[q = a_{11}x_1^2 + a_{22}x_2^2 + \cdots + a_{nn}x_n^2 + a_{12}x_1x_2+\cdots\nonumber \] Entonces, se\(q\) puede escribir de la\(q = d_{11}y_1^2 + \cdots + d_{nn}y_n^2\) siguiente manera:
- Escribir\(q = \vec{x}^T A \vec{x}\) para una matriz simétrica\(A\).
- Diagonalizar ortogonalmente\(A\) para ser escrito como\(U^TAU=D\) para una matriz ortogonal\(U\) y una matriz diagonal\(D\).
- Escribir\(\vec{y} = \left[ \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]\). Entonces,\(\vec{x} = U \vec{y}\).
- La forma cuadrática ahora\(q\) estará dada por\[q = d_{11}y_1^2 + \cdots + d_{nn}y_n^2 = \vec{y}^T D \vec{y}\nonumber \] donde\(D = \left[ d_{ij} \right]\) se encuentra la matriz diagonal al diagonalizar ortogonalmente\(A\).
Considera el siguiente ejemplo.
Considera la siguiente curva de nivel que\[6x_1^2 + 4x_1x_2 + 3x_2^2 = 7\nonumber \] se muestra en la siguiente gráfica.
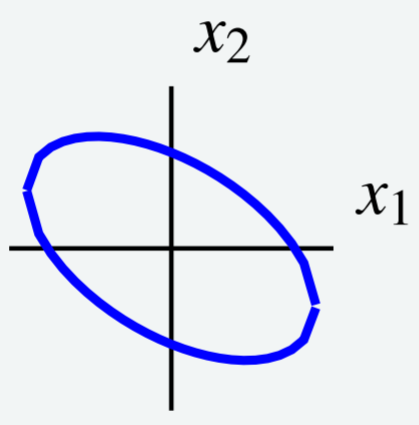
Utilice un cambio de variables para elegir nuevos ejes de tal manera que la elipse esté orientada paralela a los nuevos ejes de coordenadas. Es decir, utilizar un cambio de variables para reescribir\(q\) para eliminar el\(x_1x_2\) término.
Solución
Observe que la curva de nivel viene dada por\(q = 7\) for\(q = 6x_1^2 + 4x_1x_2 + 3x_2^2\). Esta es la misma forma cuadrática que examinamos anteriormente en Ejemplo\(\PageIndex{13}\). Por lo tanto sabemos que podemos escribir\(q = \vec{x}^T A \vec{x}\) para la matriz\[A = \left[ \begin{array}{rr} 6 & 2 \\ 2 & 3 \end{array} \right]\nonumber \]
Ahora queremos diagonalizar ortogonalmente\(U^TAU=D\) para escribir\(A\) para una matriz ortogonal\(U\) y una matriz diagonal\(D\). Los detalles se dejan al lector, y se puede verificar que las matrices resultantes son\[\begin{aligned} U &= \left[ \begin{array}{rr} \frac{2}{\sqrt{5}} & - \frac{1}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \end{array} \right] \\ D &= \left[ \begin{array}{rr} 7 & 0 \\ 0 & 2 \end{array} \right]\end{aligned}\]
A continuación escribimos\(\vec{y} = \left[ \begin{array}{c} y_1 \\ y_2 \end{array} \right]\). De ello se deduce que\(\vec{x} = U \vec{y}\).
Ahora podemos expresar la forma cuadrática\(q\) en términos de\(y\), utilizando las entradas de\(D\) como coeficientes de la siguiente manera:\[\begin{aligned} q &= d_{11}y_1^2 + d_{22}y_2^2 \\ &= 7y_1^2 + 2y_2^2 \end{aligned}\]
De ahí que se pueda escribir la curva de nivel\(7y_1^2 + 2y_2^2 =7\). La gráfica de esta ecuación viene dada por:
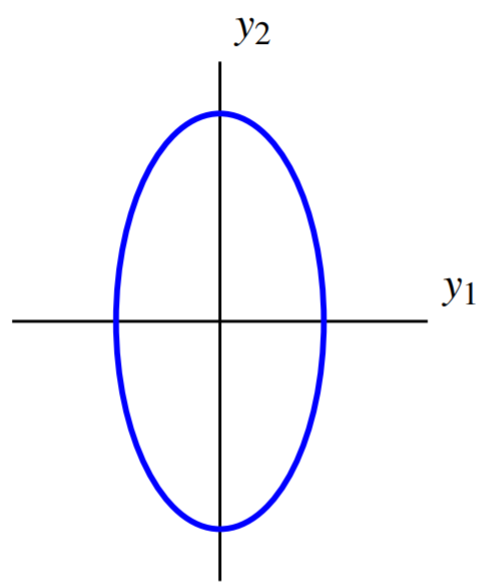
El cambio de variables da como resultado nuevos ejes de tal manera que con respecto a los nuevos ejes, la elipse se orienta paralela a los ejes de coordenadas. Estos se denominan los ejes principales de la forma cuadrática.
El siguiente es otro ejemplo de diagonalización de una forma cuadrática.
Considera la curva de nivel\[5x_1^{2}-6x_1x_2+5x_2^{2}=8\nonumber\] que se muestra en la siguiente gráfica.
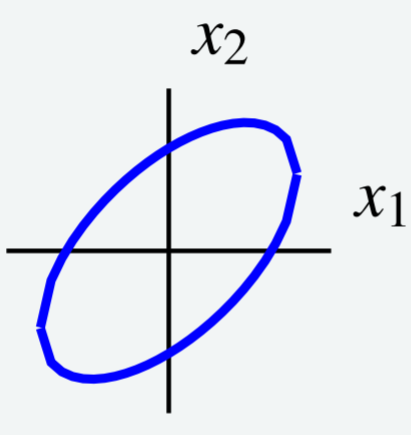
Utilice un cambio de variables para elegir nuevos ejes de tal manera que la elipse esté orientada paralela a los nuevos ejes de coordenadas. Es decir, utilizar un cambio de variables para reescribir\(q\) para eliminar el\(x_1x_2\) término.
Solución
Primero, expresar la curva de nivel como\(\vec{x}^TA\vec{x}\) dónde\(\vec{x} = \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right]\) y\(A\) es simétrica. Vamos\(A = \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]\). Entonces\(q = \vec{x}^T A \vec{x}\) es dado por\[\begin{aligned} q &= \left[ \begin{array}{cc} x_1 & x_2 \end{array} \right] \left[ \begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \left[ \begin{array}{r} x_1 \\ x_2 \end{array} \right]\\ &= a_{11}x_1^2 + (a_{12} + a_{21})x_1x_2 + a_{22}x_2^2\end{aligned}\]
Equiparando esto a la descripción dada para\(q\), tenemos\[5x_1^2 -6x_1x_2 + 5x_2^2 = a_{11}x_1^2 + (a_{12} + a_{21})x_1x_2 + a_{22}x_2^2\nonumber \] Esto implica eso\(a_{11} = 5, a_{22} = 5\) y\(A\) para que sea simétrico,\(a_{12} = a_{22} = \frac{1}{2} (a_{12}+a_{21}) = -3\). El resultado es\(A = \left[ \begin{array}{rr} 5 & -3 \\ -3 & 5 \end{array} \right]\). Podemos escribir\(q = \vec{x}^TA\vec{x}\) como\[\left[ \begin{array}{cc} x_1 & x_2 \end{array} \right] \left[ \begin{array}{rr} 5 & -3 \\ -3 & 5 \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \end{array} \right] =8\nonumber \]
A continuación, diagonalizar ortogonalmente la matriz\(A\) para escribir\(U^TAU = D\). Los detalles se dejan al lector y las matrices necesarias son dadas por\[\begin{aligned} U &= \left[ \begin{array}{rr} \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & - \frac{1}{2}\sqrt{2} \end{array} \right] \\ D &= \left[ \begin{array}{rr} 2 & 0 \\ 0 & 8 \end{array} \right]\end{aligned}\]
Escribe\(\vec{y} = \left[ \begin{array}{r} y_1 \\ y_2 \end{array} \right]\), tal que\(\vec{x} = U \vec{y}\). Entonces se deduce que\(q\) viene dada por\[\begin{aligned} q &= d_{11}y_1^2 + d_{22}y_2^2 \\ &= 2y_1^{2}+8y_2^{2}\end{aligned}\] Por lo tanto la curva de nivel se puede escribir como\(2y_1^{2}+8y_2^{2}=8\).
Se trata de una elipse paralela a los ejes de coordenadas. Su gráfica es de la forma
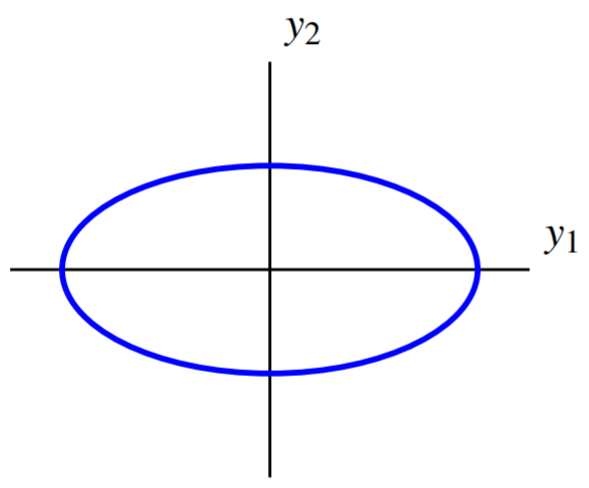
Así, este cambio de variables elige nuevos ejes de tal manera que con respecto a estos nuevos ejes, la elipse se orienta paralela a los ejes de coordenadas.


