4.7: FUNCIONES CONVEXAS Y SUBDIFERENCIALES NO
- Page ID
- 107804
En esta sección, presentamos un nuevo concepto que es útil en el estudio de problemas de optimización en los que la función objetiva puede no ser diferenciable.
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa. Un número\(u \in \mathbb{R}\) se llama subderivada de la función\(f\) at\(\bar{x}\) si\[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x \in \mathbb{R} .\] El conjunto de todas las subderivadas de\(f\) at\(\bar{x}\) se llama el subdiferencial de\(f\) at\(\bar{x}\) y se denota por\(\partial f(\bar{x})\).
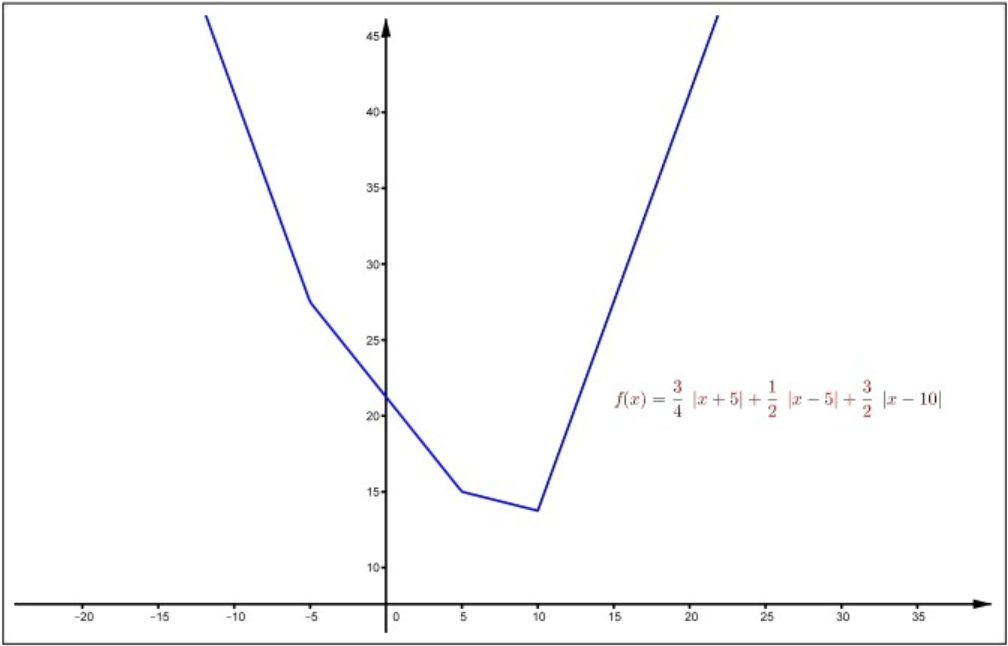
Figura\(4.7\): Una función convexa no diferencial.
Vamos\(f(x)=|x|\). Entonces\[\partial f(0)=[-1,1].\]
Solución
Efectivamente, para cualquiera\(u \in \partial f(0)\), tenemos\[u \cdot x=u(x-0) \leq f(x)-f(0)=|x| \text { for all } x \in \mathbb{R}.\] en particular,\(u \cdot 1 \leq|1|=1\) y\(u \cdot(-1)=-u \leq|-1|=1\). Así,\(u \in[-1,1]\). De ello se deduce que\[\partial f(0) \subset[-1,1].\] Para cualquiera\(u \in[-1,1]\), tenemos\(|u| \leq 1\). Entonces\[u \cdot x \leq|u \cdot x|=|u||x| \leq|x| \text { for all } x \in \mathbb{R} .\] esto implica\(u \in \partial f(0)\). Por lo tanto,\(\partial f(0)=[-1,1]\).
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa, Fix\(a \in \mathbb{R}\). Defina la función de pendiente\(\phi_{a}\) por\[\phi_{a}(x)=\frac{f(x)-f(a)}{x-a}\] for\(x \in (-\infty, a) \cup(a, \infty)\). Entonces, para\(x_{1}, x_{2} \in(-\infty, a) \cup(a, \infty)\) con\(x_{1}<x_{2}\), tenemos\[\phi_{a}\left(x_{1}\right) \leq \phi_{a}\left(x_{2}\right).\]
- Prueba
-
Este lema sigue directamente de Lemma 4.6.5. \(\square\)
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa y dejar\(\bar{x} \in \mathbb{R}\). Luego\(f\) tiene derivada izquierda y derivada derecha en\(\bar{x}\). Además,\[\sup _{x<\bar{x}} \phi_{\bar{x}}(x)=f_{-}^{\prime}(\bar{x}) \leq f_{+}^{\prime}(\bar{x})=\inf _{x>\bar{x}} \phi_{\bar{x}}(x) ,\] donde\(\phi_{\bar{x}}\) se define en (4.17).
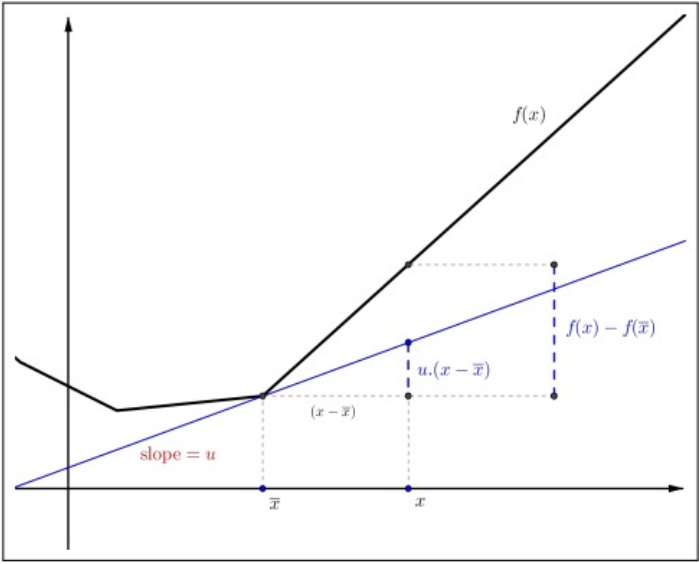
Figura\(4.8\): Definición de subderivada.
- Prueba
-
Por Lema 4.7.1, la función de pendiente\(\phi_{x}\) definida por (4.17) está aumentando en el intervalo\((\bar{x}, \infty)\) y delimitada por debajo por\(\phi_{\mathcal{K}}(\bar{x}-1)\). Por el Teorema 3.2.4, el límite\[\lim _{x \rightarrow \bar{x}^{+}} \phi_{i}(x)=\lim _{x \rightarrow \bar{x}^{+}} \frac{f(x)-f(\bar{x})}{x-\bar{x}}\] existe y es finito. Por otra parte,\[\lim _{x \rightarrow \overline{\mathbf{x}^{+}}} \phi_{x}(x)=\inf _{x>x} \phi_{x}(x) .\] Así,\(f_{+}^{\prime}(\bar{x})\) existe y\[f_{+}^{\prime}(\bar{x})=\inf _{x>x} \phi_{i}(x) .\] De igual manera,\(f_{-}^{\prime}(\bar{x})\) existe y\[f_{-}^{\prime}(\bar{x})=\sup _{x<R} \phi_{x}(x) .\] Aplicando Lema 4.7.1 de nuevo, vemos que\[\phi_{x}(x) \leq \phi_{x}(y) \text { whenever } x<\bar{x}<y .\] Esto implica\(f_{-}^{\prime}(\bar{x}) \leq f_{+}^{\prime}(\bar{x})\). La prueba está completa. \(\square\)
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa y dejar\(\bar{x} \in \mathbb{R}\). Entonces\[\partial f(\bar{x})=\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right] .\]
- Prueba
-
Supongamos\(u \in \partial f(\bar{x})\). Por la definición (4.16), tenemos\[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x>\bar{x} .\] Esto implica\[u \leq \frac{f(x)-f(\bar{x})}{x-\bar{x}} \text { for all } x>\bar{x} .\] Así,\[u \leq \lim _{x \rightarrow \bar{x}^{+}} \frac{f(x)-f(\bar{x})}{x-\bar{x}}=f_{+}^{\prime}(\bar{x}) .\] Similarmente, tenemos\[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x<\bar{x} .\] Así,\[u \geq \frac{f(x)-f(\bar{x})}{x-\bar{x}} \text { for all } x<\bar{x} .\] Esto implica\(u \geq f_{-}^{\prime}(\bar{x})\). Entonces\[\partial f(\bar{x}) \subset\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right] .\] Para probar la inclusión opuesta,\(u \in\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right]\) tomar. por Teorema 4.7.2\[\sup _{x<x} \phi_{\bar{x}}(x)=f_{-}^{\prime}(\bar{x}) \leq u \leq f_{+}^{\prime}(\bar{x})=\inf _{x>\bar{x}} \phi_{\bar{x}}(x) .\] Usando la estimación superior por\(f_{+}^{\prime}(\bar{x})\) for\(u\),\[u \leq \phi_{\bar{x}}(x)=\frac{f(x)-f(\bar{x})}{x-\bar{x}} \text { for all } x>\bar{x} .\] se tiene De ello se deduce que\[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x \geq \bar{x} .\] De igual manera, uno también tiene\[u \cdot(x-\bar{x}) \leq f(x)-f(\bar{x}) \text { for all } x<\bar{x} .\] Así, (4.16) sostiene y, por lo tanto,\(u \in \partial f(\bar{x})\). Por lo tanto, (4.18) sostiene. \(\square\)
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa y\(\bar{x} \in \mathbb{R}\). Entonces\(f\) es diferenciable en\(\bar{x}\) si y solo si\(\partial f(\bar{x})\) es un singleton. En este caso,\[\partial f(\bar{x})=\left\{f^{\prime}(\bar{x})\right\} .\]
- Prueba
-
Supongamos que\(f\) es diferenciable en\(\bar{x}\). Entonces\[f_{-}^{\prime}(\bar{x})=f_{+}^{\prime}(\bar{x})=f^{\prime}(\bar{x}).\] Por Teorema 4.7.3,\[\partial f(\bar{x})=\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right]=\left\{f^{\prime}(\bar{x})\right\} .\] Así,\(\partial f(\bar{x})\) es un singleton.
Por el contrario, si\(\partial f(\bar{x})\) es un singleton, debemos tener\(f_{-}^{\prime}(\bar{x})=f_{+}^{\prime}(\bar{x})\). Por lo tanto,\(f\) es diferentaible en\(\bar{x}\). \(\square\)
Vamos\(f(x)=a|x-b|+c\), dónde\(a > 0\).
Solución
Entonces\(f\) es una función convexa y\[f_{-}^{\prime}(b)=-a, f_{+}^{\prime}(b)=a .\] Así,\[\partial f(b)=[-a, a] .\] ya que\(f\) es diferenciable on\((-\infty, b)\) y\((b, \infty)\), tenemos\ [\ parcial f (x) =\ left\ {\ begin {array} {ll}
\ {-a\}, &\ text {if} x<b\ text {;}\\
{[-a, a],} &\ text {if} x=b\ text {;}\\
\ {a\}, &\ texto {si} x>b\ texto {.}
\ end {array}\ derecho.\]
Dejar\(A\) y\(B\) ser dos subconjuntos no vacíos de\(\mathbb{R}\) y\(\alpha \in \mathbb{R}\). Definir\[A+B=\{a+b: a \in A, b \in B\} \text { and } \alpha A=\{\alpha a: a \in A\} .\]
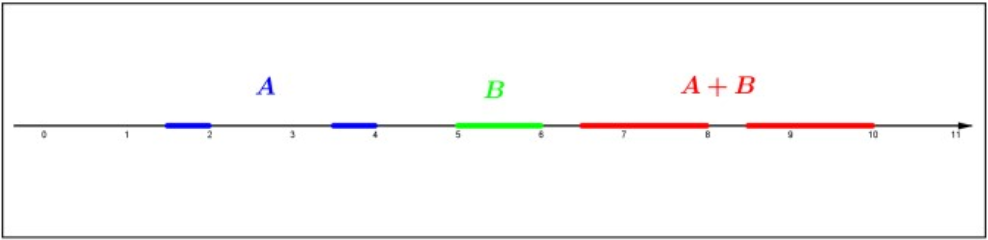
Figura\(4.9\): Conjunto de adición.
Dejar\(f, g: \mathbb{R} \rightarrow \mathbb{R}\) ser funciones convexas y dejar\(\alpha > 0\). Entonces\(f + g\) y\(\alpha f\) son funciones convexas y\ [\ begin {array} {l}
\ parcial (f+g) (\ bar {x}) =\ parcial f (\ bar {x}) +\ parcial g (\ bar {x})\
\ parcial (\ alpha f) (\ bar {x}) =\ alfa\ parcial f (\ bar {x})\ texto {.}
\ end {array}\]
- Prueba
-
No es difícil ver que\(f + g\) es una función convexa y\ [\ begin {array} {l}
(f+g) _ {+} ^ {\ prime} (\ bar {x}) =f_ {+} ^ {\ prime} (\ bar {x}) +g_ {+} ^ {\ prime} (\ bar {x})\\
(f+g) _ {-} ^ {prime\} (\ bar {x}) =f_ {-} ^ {\ prime} (\ bar {x}) +g_ {-} ^ {\ prime} (\ bar {x})\ texto {.}
\ end {array}\] Por teorema 4.7.3,\ [\ begin {alineado}
\ parcial (f+g) (\ bar {x}) &=\ left [(f+g) _ {-} ^ {\ prime} (\ bar {x}), (f+g) _ {+} ^ {\ prime} (\ bar {x})\ derecha]\\
&= izquierda [f_ {-} ^ {\ prime} (\ bar {x}) +g_ {-} ^ {\ prime} (\ bar {x}), f_ {+} ^ {\ prime} (\ bar {x}) +g_ {+} ^ {\ prime} (\ bar { x})\ derecha]\\
&=\ izquierda [f_ {-} ^ {\ prime} (\ bar {x}), f_ {+} ^ {\ prime} (\ bar {x})\ derecha] +\ izquierda [g_ {-} ^ {\ prime} (\ bar {x}), g_ {+} ^ {\ prime} (\ bar {x})\ derecha]\\
&=\ parcial f (\ bar {x}) +\ parcial g (\ barra {x})\ texto {.}
\ end {aligned}\] La prueba para la segunda fórmula es similar. \(\square\)
Dejar\(a_{1}<a_{2}<\cdots<a_{n}\) y dejar\(\mu_{i}>0\) para\(i=1, \ldots, n\). Definir\[f(x)=\sum_{i=1}^{n} \mu_{i}\left|x-a_{i}\right| .\]
Solución
Entonces\(f\) es una función convexa. Por Teorema 4.7.5, obtenemos\ [\ parcial f (\ bar {x}) =\ izquierda\ {\ comenzar {array} {ll}
\ sum_ {a_ {i} <\ bar {x}}\ mu_ {i} -\ sum_ {a_ {i} >\ bar {x}}\ mu_ {i}, &\ texto {si}\ bar {x}\ notin\ izquierda\ {a_ {1},\ ldots, a_ {n}\ derecha\}\
\ suma_ {a_ {i} <\ bar {x}}\ mu_ {i} -\ sum_ {a_ {i} >\ bar {x}}\ mu_ {i} +\ izquierda [-\ mu_ {i_ {0} },\ mu_ {i_ {0}}\ derecho], &\ texto {si}\ bar {x} =a_ {i_ {0}}\ texto {.}
\ end {array}\ derecho.\]
Dejar\(f_{i}: \mathbb{R} \rightarrow \mathbb{R}\),\(i=1, \ldots, n\), ser funciones convexas. Definir\[f(x)=\max \left\{f_{i}(x): i=1, \ldots, n\right\} \text { and } I(u)=\left\{i=1, \ldots, n: f_{i}(u)=f(u)\right\} .\] Entonces\(f\) es una función convexa. Además,\[\partial f(\bar{x})=[m, M],\] donde\[m=\min _{i \in I(\bar{x})} f_{i-}^{\prime}(\bar{x}) \text { and } M=\max _{i \in I(\bar{x})} f_{i+}^{\prime}(\bar{x}) .\]
- Prueba
-
Fijar\(u, v \in \mathbb{R}\) y\(\lambda \in (0, 1)\). Para cualquiera\(i=1, \ldots, n\), tenemos\[f_{i}(\lambda u+(1-\lambda) v) \leq \lambda f_{i}(u)+(1-\lambda) f_{i}(v) \leq \lambda f(u)+(1-\lambda) f(v) .\] Esto implica\[f(\lambda u+(1-\lambda) v)=\max _{1 \leq i \leq n} f_{i}(\lambda u+(1-\lambda) v) \leq \lambda f(u)+(1-\lambda) f(v) .\] Así,\(f\) es una función convexa. De igual manera verificamos que\(f_{+}^{\prime}(\bar{x})=M\) y\(f_{-}^{\prime}(\bar{x})=m\). Por Teorema 4.7.3,\[\partial f(\bar{x})=[m, M] .\] La prueba ya está completa. \(\square\)
el producto de dos funciones convexas no es una función convexa en general. Por ejemplo,\(f(x) = x\) y\(g(x) = x^{2}\) son funciones convexas, pero no\(h(x)=x^{3}\) es una función convexa.
El siguiente resultado puede considerarse como una versión de la primera prueba derivada para extremos en el caso de funciones no diferenciables.
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa. Entonces\(f\) tiene un mínimo absoluto en\(\bar{x}\) si y solo si\[0 \in \partial f(\bar{x})=\left[f_{-}^{\prime}(\bar{x}), f_{+}^{\prime}(\bar{x})\right] .\]
- Prueba
-
Supongamos que\(f\) tiene un mínimo absoluto en\(\bar{x}\). Entonces\[f(\bar{x}) \leq f(x) \text { for all } x \in \mathbb{R} .\] Esto implica\[0 \cdot(x-\bar{x})=0 \leq f(x)-f(\bar{x}) \text { for all } x \in \mathbb{R} .\] Se deduce de (4.16) que\(0 \in \partial f(\bar{x})\).
Por el contrario\(0 \in \partial f(\bar{x})\), si, de nuevo, por (4.16),\[0 \cdot(x-\bar{x})=0 \leq f(x)-f(\bar{x}) \text { for all } x \in \mathbb{R} .\] Así,\(f\) tiene un mínimo absoluto en\(\bar{x}\). \(\square\)
Dejar\(k\) ser un entero positivo y\(a_{1}<a_{2}<\cdots<a_{2 k-1}\). Definir\[f(x)=\sum_{i=1}^{2 k-1}\left|x-a_{i}\right| ,\] para\(x \in \mathbb{R}\).
Solución
De la fórmula subdiferencial del Ejemplo 4.7.3 se deduce que\(0 \in \partial f(\bar{x})\) si y sólo si\(\bar{x}=a_{k}\). Así,\(f\) tiene un mínimo absoluto único en\(a_{k}\).
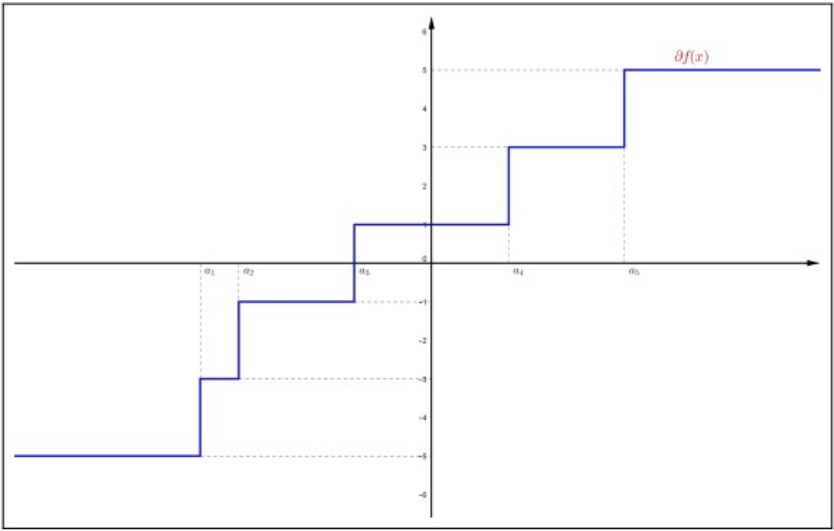
Figura\(4.10\): Subdiferencial de\(f(x)=\sum_{i=1}^{2 k-1}\left|x-a_{i}\right|\).
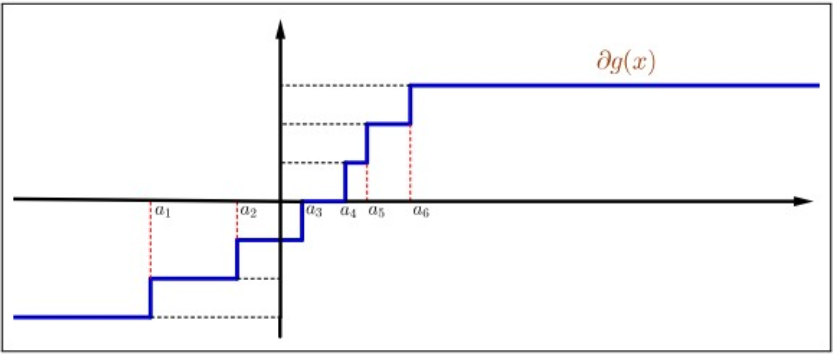
Figura\(4.11\): Subdiferencial de\(g(x)=\sum_{i=1}^{2 k}\left|x-a_{i}\right|\).
Del mismo modo, si\(a_{1}<a_{2}<\cdots<a_{2 k}\) y\[g(x)=\sum_{i=1}^{2 k}\left|x-a_{i}\right| .\] Entonces\(0 \in \partial g(\bar{x})\) si y solo si\(\bar{x} \in\left[a_{k}, a_{k+1}\right]\). Así,\(g\) tiene un mínimo absoluto en cualquier punto de\(\left[a_{k}, a_{k+1}\right]\).
El siguiente teorema es una versión del Teorema del Valor Medio (Teorema 4.2.3) para funciones no diferenciables.
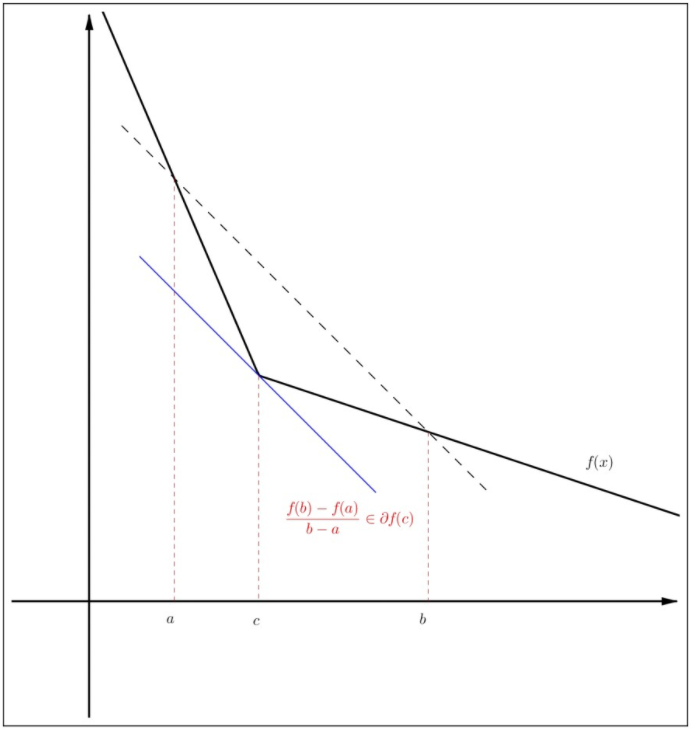
Figura\(4.12\): Teorema del valor medio subdiferencial.
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa y dejar\(a < b\). Entonces existe\(c \in (a, b)\) tal que\[\frac{f(b)-f(a)}{b-a} \in \partial f(c) .\]
- Prueba
-
Definir\[g(x)=f(x)-\left[\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\right] .\] Entonces\(g\) es una función convexa y\(g(a)=g(b)\). Así,\(g\) tiene un mínimo local en algunos\(c \in (a, b)\) y, por lo tanto,\(g\) también tiene un mínimo absoluto en\(c\). Observe que la función\[h(x)=-\left[\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\right]\] es diferenciable en\(c\) y,\[\partial h(c)=\left\{h^{\prime}(c)\right\}=\left\{-\frac{f(b)-f(a)}{b-a}\right\} .\] por lo tanto, Por Teorema 4.7.8 y la regla de suma subdiferencial,\[0 \in \partial g(c)=\partial f(c)-\left\{\frac{f(b)-f(a)}{b-a}\right\} .\] Esto implica (4.19). La prueba ya está completa. \(\square\)
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa. Entonces Lipschitz\(f\) es continuo si y solo si existe\(\ell \geq 0\) tal que\[\partial f(x) \subset[-\ell, \ell] \text { for all } x \in \mathbb{R} .\]
- Prueba
-
Supongamos\(f\) que Lipschitz es continuo en\(\mathbb{R}\). Entonces existe\(\ell \geq 0\) tal que\[|f(u)-f(v)| \leq \ell|u-v| \text { for all } u, v \in \mathbb{R} .\] Entonces para cualquier\(x \in \mathbb{R}\),\[f_{+}^{\prime}(x)=\lim _{h \rightarrow 0^{+}} \frac{f(x+h)-f(x)}{h} \leq \lim _{h \rightarrow 0^{+}} \frac{\ell|h|}{h}=\ell .\] De igual manera,\(f_{-}^{\prime}(x) \geq-\ell\). Así, a\[\partial f(x)=\left[f_{-}^{\prime}(x), f_{+}^{\prime}(x)\right] \subset[-\ell, \ell] .\] la inversa, arreglar cualquiera\(u, v \in \mathbb{R}\) con\(u \neq v\). Aplicando el Teorema 4.7.9, obtenemos\[\frac{f(v)-f(u)}{v-u} \in \partial f(c) \subset[-\ell, \ell] ,\] para algunos\(c\) en el medio\(u\) y\(v\). Esto implica\[|f(u)-f(v)| \leq \ell|u-v| .\] Esta desigualdad obviamente se sostiene para\(u = v\). Por lo tanto,\(f\) es Lipschitz continuo. \(\square\)
Ejercicio\(\PageIndex{1}\)
Encuentra subdiferenciales de las siguientes funciones:
- \(f(x)=a|x|\),\(a > 0\).
- \(f(x)=|x-1|+|x+1|\).
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{2}\)
Encuentra el subdiferencial de la función\[f(x)=\max \{-2 x+1, x, 2 x-1\} .\]
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{3}\)
Vamos\(f(x)=\sum_{k=1}^{n}|x-k|\). Encuentra todos los minimizadores absolutos de la función.
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{4}\)
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa. Fijar\(a, b \in \mathbb{R}\) y definir la función\(g\) por\[g(x)=f(a x+b), \text { for } x \in \mathbb{R}\] Demostrar eso\(\partial g(\bar{x})=a \partial f(a \bar{x}+b)\).
- Responder
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{5}\)
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función convexa. Supongamos que\(\partial f(x) \subset[0, \infty)\) para todos\(x \in \mathbb{R}\). Demostrar que\(f\) es monótona aumentando en\(\mathbb{R}\).
- Responder
-
Agrega textos aquí. No elimine primero este texto.