1.1: Números reales y racionales
- Page ID
- 109464
- Explicación de los números reales y racionales
El conjunto de números reales (denotado,\(\Re\)) está mal llamado. Los números reales no son más o menos reales —en el sentido no matemático de que existen— que cualquier otro conjunto de números, al igual que el conjunto de números racionales (\(\mathbb{Q}\)), el conjunto de números enteros (\(\mathbb{Z}\)), o el conjunto de números naturales (\(\mathbb{N}\)). El nombre de “números reales” es (casi) una anomalía histórica no muy diferente del nombre “Teorema de Pitágoras” que en realidad se conocía y entendía mucho antes de que viviera Pitágoras.
Cuando se inventaba el cálculo en el\(17^{th}\) siglo, los números se entendían a fondo, o eso se creía. Ellos eran, después de todo, solo números. Combínalos. A eso lo llamamos adición. Si los agregas repetidamente lo llamamos multiplicación. La resta y la división se entendieron de manera similar.
Fue (y sigue siendo) útil visualizar estas cosas de una manera más concreta. Si tomamos una vara de longitud\(2\) y otra de longitud\(3\) y las colocamos de extremo a extremo obtenemos una longitud de\(5\). Esto es adición. Si los colocamos de extremo a extremo pero en ángulo recto entonces nuestros dos palos son el largo y ancho de un rectángulo cuya área es\(6\). Esto es multiplicación.
Por supuesto, medir longitudes con números enteros tiene limitaciones, pero estas no son difíciles de arreglar. Si tenemos una longitud (palo) de longitud\(1\) y otra de longitud\(2\), entonces podemos encontrar otra cuya longitud cuando se compara con\(1\) es la misma (tiene la misma proporción que) que\(1\) es a\(2\). Ese número por supuesto, es\(1/2\).
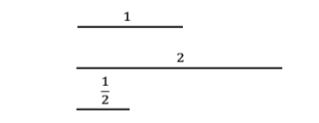
Figura\(\PageIndex{1}\): Largo de palo.
Observe cómo la notación de fracciones refleja la operación de\(1\) comparar con\(2\). Esta comparación generalmente se conoce como la relación de\(1\) a,\(2\) por lo que los números de este tipo se denominan números racionales. El conjunto de números racionales se denota\(\mathbb{Q}\) para cocientes. En la primaria te fueron presentados como fracciones. Una vez entendidas las fracciones, esta visualización usando segmentos de línea (sticks) conduce de manera bastante natural a su representación con la recta numérica racional.

Figura\(\PageIndex{2}\): Línea numérica racional.
Esto parece funcionar como una visualización porque los puntos en una línea y los números racionales comparten ciertas propiedades. El principal de estos es que entre dos puntos cualesquiera de la línea racional hay otro punto, así como entre dos números racionales cualesquiera hay otro número racional.
Dejar\(a,b,c,d ∈ N\) y encontrar un número racional entre\(a/b\) y\(c/d\).
Todo esto es muy limpio y satisfactorio hasta que lo examinamos un poco más de cerca. Entonces se vuelve bastante misterioso. Consideremos de nuevo los números racionales\(a/b\) y\(c/d\). Si pensamos en estos como longitudes podemos preguntar: “¿Hay una tercera longitud, digamos\(α\), tal que podamos\(a/b\) dividir en\(M\) pedazos, cada uno de largo\(α\) y también dividir\(c/d\) en\(N\) trozos cada uno de largo\(α\)? “Unos minutos pensaron debería convencerte de que esto es lo mismo que el problema de encontrar un denominador común así que\(α = \frac{1}{bd}\) va a funcionar muy bien. (Confirme esto usted mismo.)
Quizás te estés preguntando por qué estamos haciendo todo este alboroto. Obviamente esto siempre es cierto. De hecho el párrafo anterior da un bosquejo de una pequeña prueba muy agradable de ello. Aquí están el teorema y su prueba presentada formalmente.
Dejar\(a\),\(b\),\(c\), y\(d\) ser enteros. Hay un número\(α ∈ Q\) tal que\(Mα = a/b\) y\(Nα = c/d\) dónde\(M\) y también\(N\) son enteros.
Prueba:
Para probar este teorema vamos a mostrar\(α\),\(M\) y\(N\). Es su responsabilidad confirmar que estos realmente funcionan. Aquí están:\(α = 1/bd\),\(M = ad\), y\(N = cb\).
Confirmar que\(α\),\(M\), y\(N\) como se da en la prueba de Teorema\(\PageIndex{1}\) satisfacer los requisitos del teorema.
Debe quedar claro que es necesario para\(a\),\(b\)\(c\),, y\(d\) ser enteros para que todo funcione. De lo contrario\(M\) y no\(N\) serán también enteros como se requiera.
Esto sugiere la siguiente pregunta muy profunda e importante: ¿Hay longitudes que no pueden expresarse como la relación de dos longitudes enteras? La respuesta, por supuesto, es sí. De lo contrario no hubiéramos hecho la pregunta. Observe que para tales números nuestra prueba de Teorema no\(\PageIndex{1}\) es válida (¿por qué no?).
Uno de los ejemplos más conocidos de tal número es la circunferencia de un círculo con diámetro\(1\). Este es el número generalmente denotado por\(π\). Pero los círculos son objetos extremadamente complejos —sólo parecen simples porque son muy familiares. Surgiendo como lo hace de un círculo, se esperaría que el número\(π\) también sea muy complejo y esto es cierto. De hecho\(π\) es un número excepcionalmente extraño por una variedad de razones. Empecemos con algo un poco más fácil de pensar.
Los cuadrados son simples. Dos juegos de líneas paralelas en ángulo recto, todas de la misma longitud. ¿Qué podría ser más sencillo? Si construimos un cuadrado con lados que tienen longitud\(1\) entonces su diagonal tiene longitud\(\sqrt{2}\).
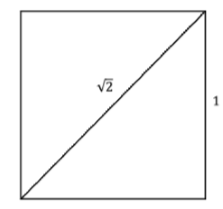
Figura\(\PageIndex{3}\): Cuadrada.
Se trata de un número que no se puede expresar como la relación de dos números enteros. Es decir, es irracional. Esto se sabe desde la antigüedad, pero sigue siendo bastante desconcertante cuando se encuentra por primera vez. Parece tan contraintuitivo que el intelecto se rebela. “Esto no puede estar bien”, dice. “¡Eso es una locura! ”
Sin embargo es cierto y podemos probar que es cierto de la siguiente manera.
¿Qué pasa si suponemos que la raíz cuadrada de dos se puede expresar como una relación de enteros? Demostraremos que esto lleva irrevocablemente a una conclusión que manifiestamente no es cierta.
Supongamos\(\sqrt{2} = a/b\) dónde\(a\) y\(b\) son enteros. Supongamos además que la fracción\(a/b\) está en términos más bajos. Esta suposición es crucial porque si\(a/b\) es en términos más bajos sabemos que a lo sumo sólo uno de ellos es parejo.
Entonces
\[\frac{a}{b} = \sqrt{2}\]
Al cuadrar ambos lados, se obtiene:
\[a^2 = 2b^2\]
Por lo tanto\(a^2\) es parejo. Pero si\(a^2\) es aún entonces un debe ser incluso también (¿por qué?). Si a es par entonces\(a = 2k\) para algún entero\(k\). Por lo tanto
\[4k^2 = 2b^2\]
o
\[2k^2 = b^2\]
Por lo tanto también\(b^2\) es parejo y así\(b\) debe ser incluso también. Pero esto es imposible. Acabamos de concluir que\(a\) y\(b\) son ambos parejos y esta conclusión se deriva directamente de nuestra suposición inicial de que a lo sumo uno de ellos podría ser parejo.
Esto es una tontería. ¿Dónde está nuestro error? No está en ningún paso de nuestro razonamiento. Todo eso fue sólido. Compruébalo de nuevo para estar seguro.
Por lo tanto nuestro error debe estar en el supuesto inicial que\(\sqrt{2}\) podría expresarse como una fracción. Por lo tanto, esa suposición debe ser falsa. En otras palabras,\(\sqrt{2}\) no se puede expresar así.
Demostrar que cada uno de los siguientes números es irracional:
- \(\sqrt{3}\)
- \(\sqrt{5}\)
- \(\sqrt[3]{2}\)
- \(i(= \sqrt{-1}) \)
- La raíz cuadrada de cada entero positivo que no es el cuadrado de un entero.
El hecho de que\(\sqrt{2}\) no sea racional es lindo e interesante, pero a menos que, al igual que los pitagóricos de la antigua Grecia, tengan una convicción religiosa fuertemente arraigada de que todos los números son racionales, no parece terriblemente importante. Por otro lado, la existencia misma de\(\sqrt{2}\) plantea algunas preguntas interesantes. Por ejemplo, ¿qué puede significar\(4^{\sqrt{2}}\) el símbolo? Si el exponente fuera un número racional, digamos\(m/n\), entonces claramente\(4^{m/n} = \sqrt[n]{4^m}\). Pero ya que\(\sqrt{2} \neq m/n\) para cualquier número entero m y n ¿cómo interpretamos\(4^{\sqrt{2}}\)? ¿Tiene algún significado en absoluto?
Cuanto más se piensa en esto, más desconcertante se vuelve la existencia de números irracionales. Supongamos por ejemplo que reconsideramos la construcción de un segmento de línea de longitud\(\sqrt{2}\). Es claro que la construcción funciona y que realmente podemos construir tal segmento de línea. Existe.
Repite la construcción pero esta vez pongamos el lado base en la línea racional.
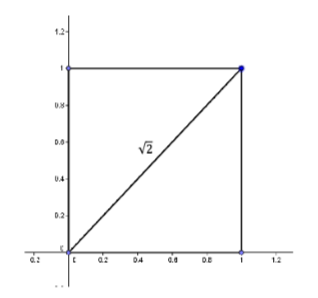
Figura\(\PageIndex{4}\): Construcción de un segmento lineal de longitud\(\sqrt{2}\) con el lado base sobre la línea racional.
Sabemos que la diagonal de este cuadrado es\(\sqrt{2}\) como se indica. Y sabemos que no\(\sqrt{2}\) es un número racional.
Ahora deja la diagonal anclada en\((0,0)\) pero deja que gire hacia abajo para que coincida con el\(x\) eje −axis.

Figura\(\PageIndex{5}\): Diagonal girada hacia abajo para coincidir con el eje x.
El final de nuestra diagonal trazará un arco del círculo con radio\(\sqrt{2}\). Cuando la diagonal coincide con el\(x\) eje −, su punto final obviamente será el punto\((\sqrt{2} ,0)\) como se muestra.
¡Pero espera! Estamos usando la línea numérica racional para nuestro\(x\) eje −axis. Eso significa que los únicos puntos en el\(x\) eje −son aquellos que corresponden a números racionales (fracciones). ¡Pero sabemos que eso no\(\sqrt{2}\) es racional! Conclusión: No tiene sentido\((\sqrt{2} ,0)\). Simplemente no existe.
Dicho de otra manera, hay un agujero en la recta numérica racional justo donde\(\sqrt{2}\) debería estar. ¡Esto es raro!
Recordemos que entre dos números racionales cualesquiera siempre hay otro. Este hecho es lo que nos llevó a representar los números racionales con una línea en primer lugar.

Figura\(\PageIndex{6}\): Línea numérica racional.
Pero es incluso peor que eso. Es sencillo demostrar que\(\sqrt{3}\),\(\sqrt{5}\), etc. son todos irracionales también. Así son\(π\) y\(e\), aunque no son tan fáciles de mostrar. Parece que la línea racional tiene un montón de agujeros en ella. Infinitamente muchos. Y sin embargo, el siguiente teorema es cierto.
- Entre dos números reales distintos hay un número racional.
- Entre dos números reales distintos hay un número irracional.
Ambas partes de este teorema se basan en un uso juicioso de lo que ahora se llama la Propiedad Arquímedea del Sistema Numérico Real, que se puede afirmar formalmente de la siguiente manera.
Dados dos números reales positivos cualesquiera\(b\),\(a\) y, hay un entero positivo,\(n\) tal que\(na > b\).
Físicamente esto dice que podemos vaciar un océano\(b\) con una cucharadita a, siempre que estemos dispuestos a usar la cucharilla una gran cantidad de veces\(n\).
Este es un concepto tan intuitivamente sencillo que es fácil aceptarlo sin pruebas. Hasta la invención del cálculo, e incluso por algún tiempo después de eso, simplemente se asumió. Sin embargo, a medida que los problemas fundamentales planteados por los conceptos de cálculo fueron entendidos y resueltos, finalmente fuimos conducidos a una comprensión más profunda de las complejidades del sistema numérico real. La Propiedad Arquímedea ya no se toma como un axioma no probado, sino que ahora se entiende como consecuencia de otros axiomas. Esto lo mostraremos más adelante, pero por ahora lo aceptaremos como obviamente cierto tal como lo hizo Arquímedes.
Con la invención del cálculo, los matemáticos del siglo XVII comenzaron a utilizar objetos que no satisfacían la Propiedad de Arquímedes (de hecho, también lo hizo Arquímedes). Como veremos en el siguiente capítulo, cuando Leibniz escribió el primer trabajo sobre su versión del cálculo, siguió esta práctica estableciendo explícitamente reglas para manipular cantidades infinitamente pequeñas (infinitesimales). Estos fueron tomados como números reales que no son cero y aún más pequeños que cualquier número real. La notación que utilizó fue\(dx\) (un desplazamiento infinitamente pequeño en la\(x\) dirección), y\(dy\) (un desplazamiento infinitamente pequeño en la\(y\) dirección). Estos símbolos deberían parecerle familiares. Son los mismos\(dy\) y\(dx\) se utilizan para formar el símbolo derivado\(\frac{\mathrm{d} y}{\mathrm{d} x}\) que aprendiste en el cálculo.
Los matemáticos de los siglos XVII y XVIII hicieron asombrosos avances científicos y matemáticos explotando estos infinitesimales, a pesar de que eran fundadamente sospechosos. No importa cuántas veces le añadas el infinitesimal\(dx\) a sí mismo el resultado no será mayor que, digamos\(10^{-1000}\), que es muy extraño.
Cuando los temas fundacionales salieron a la vanguardia, los infinitesimales cayeron algo en desgracia. Probablemente no los usaste mucho en el cálculo. La mayoría de las veces probablemente usaste la notación prime,\(f'(x)\) introducida por Lagrange en el siglo XVIII. Algunos de los temas de este libro son: Por qué los diferenciales cayeron en desgracia, con qué se reemplazaron y cómo evolucionaron con el tiempo las notaciones modernas que aprendiste en el cálculo.
Para concluir esto aparte sobre la Propiedad Arquímedea, la idea de infinitesimales fue revisitada en el siglo XX por el lógico Abraham Robinson. Robinson pudo poner la idea de infinitesimales sobre una sólida base lógica. Pero en el\(18^{th}\) siglo, la existencia de números infinitesimales era temblorosa por decir lo menos. Sin embargo esto no impidió que los matemáticos explotaran con éxito estas cantidades infinitamente pequeñas.
Volveremos a esta saga en capítulos posteriores, pero por ahora volvemos al Teorema\(\PageIndex{2}\).
Vamos a delinear la prueba de la parte (a) del Teorema\(\PageIndex{2}\) e indicaremos cómo se puede utilizar para probar la parte (b).
Dejar\(α\) y\(β\) ser números reales con\(α > β\). Hay dos casos.
- Caso 1:\(α - β > 1\). En este caso hay al menos un entero entre\(α\) y\(β\). Como los enteros son racionales estamos hechos.
- Caso 2:\(α - β ≤ 1\). En este caso, por la Propiedad de Arquímedes hay un entero positivo, digamos\(n\), tal que\(n(α - β) = nα - nβ > 1\). Ahora habrá un entero entre\(nα\) y\(nβ\). Ahora deberías poder encontrar un número racional entre\(α\) y\(β\).
Para la parte (b), dividir\(α\) y\(β\) por cualquier número irracional positivo y aplicar la parte (a). Hay un par de detalles a tener en cuenta. Estos se consideran en el siguiente problema.
- Demostrar que el producto de un número racional distinto de cero y un número irracional es irracional.
- Convertir las ideas anteriores en una prueba de Teorema\(\PageIndex{2}\).
Como cuestión práctica, la existencia de números irracionales no es realmente muy importante. A la luz del teorema\(\PageIndex{2}\), cualquier número irracional puede aproximarse arbitrariamente de cerca por un número racional. Entonces, si estamos diseñando un puente y\(\sqrt{2}\) es necesario, solo usamos\(1.414\) en su lugar. El error introducido es menor que\(0.001 = 1/1000\) así que probablemente no importa.
Pero desde un punto de vista teórico esto es devastador. Cuando se inventó el cálculo, los números racionales de repente no estaban a la altura de la tarea de justificar los conceptos y operaciones con las que necesitábamos trabajar.
Newton fundó explícitamente su versión del cálculo partiendo del supuesto de que podemos pensar en cantidades variables como generadas por un movimiento continuo. Si nuestro sistema numérico tiene agujeros en él tal movimiento continuo es imposible porque no tenemos forma de saltar por encima de los huecos. Entonces Newton simplemente postuló que no había agujeros. Llenó el hoyo donde\(\sqrt{2}\) debería estar. Simplemente dijo, sí hay un número ahí llamado\(\sqrt{2}\) e hizo lo mismo con todos los demás agujeros.
Para estar seguros no hay registro de Newton diciendo explícitamente: “Así es como voy a llenar los agujeros en la recta numérica racional. ” Junto con todos los demás en ese momento, simplemente asumió que no había agujeros y avanzó. Se necesitaron unos\(200\) años de desconcertación y discusión sobre las contradicciones, anomalías y paradojas para resolver las consecuencias de esa suposición aparentemente simple. Es posible que la tarea aún no se haya cumplido plenamente, pero para el\(20^{th}\) siglo se entendieron bien las propiedades del sistema numérico real (\(\mathbb{R}\)) como extensión del sistema numérico racional (\(\mathbb{Q}\)). Aquí están ambos sistemas visualizados como líneas:
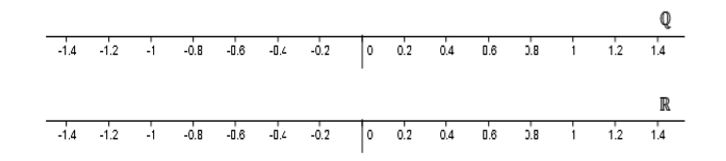
Figura\(\PageIndex{7}\): Sistemas numéricos reales y racionales.
Impresionante, ¿no? La razón por la que se parecen, a excepción\(\mathbb{R}\) de las etiquetas\(\mathbb{R}\) y por supuesto, es que nuestra capacidad para dibujar bocetos de los objetos que estamos estudiando falla por completo cuando tratamos de dibujar\(\mathbb{R}\), como diferente de\(\mathbb{Q}\). Todos los agujeros en\(\mathbb{R}\) realmente están ahí, pero los no agujeros están empaquetados tan estrechamente que no podemos separarlos en un dibujo. Esta incapacidad para esbozar los objetos que estudiamos será una fuente frecuente de frustración.
Por supuesto, esto no nos impedirá dibujar bocetos. Cuando hagamos nuestra imaginación nos salvará porque es posible imaginarlo\(\mathbb{Q}\) como distinto de\(\mathbb{R}\). Pero guarda la idea de que un boceto es una representación precisa de cualquier cosa. En el mejor de los casos nuestros bocetos solo serán ayudas a la imaginación.
Entonces, en este punto simplemente asumiremos la existencia de los números reales. Supondremos también que tienen todas las propiedades a las que estamos acostumbrados. Esto es perfectamente aceptable siempre y cuando hagamos explícitas nuestras suposiciones. Sin embargo hay que ser conscientes de que, hasta el momento, la existencia y las propiedades de los números reales es una suposición que no se ha derivado lógicamente. Cada vez que hacemos una suposición necesitamos estar preparados para abandonarla por completo si encontramos que conduce a resultados sin sentido, o para reexaminar la suposición a la luz de estos resultados para ver si podemos encontrar otra suposición que subsume la primera y explique los resultados (aparentemente) sin sentido.

