4.1: Definiciones básicas
- Page ID
- 113892
Ahora consideraremos funciones cuyos dominios y rangos son conjuntos en algunos espacios métricos fijos (pero por lo demás arbitrarios)\((S, \rho)\) y\(\left(T, \rho^{\prime}\right),\) respectivamente. Escribimos
\[f : A \rightarrow\left(T, \rho^{\prime}\right)\]
para una función\(f\) con\(D_{f}=A \subseteq(S, \rho)\) y\(D_{f}^{\prime} \subseteq\left(T, \rho^{\prime}\right) . \quad S\) se llama el espacio de dominio, y\(T\) el espacio de rango, de\(f .\)
I. Dada tal función, muchas veces tenemos que investigar su “comportamiento local” cerca de algún punto\(p \in S .\) En particular, si se\(p \in A=D_{f}(\text { so that } f(p) \text { is defined) we }\) puede preguntar: ¿Es posible hacer que los valores de la función estén tan cerca\(f(x)\) como nos guste (\(" \varepsilon -\)cerca”)\(f(p)\) manteniendo\(x\) suficientemente cerca \(\left(\text { "close }^{\prime \prime}\right)\)a\(p,\) i.e., dentro de algún globo suficientemente pequeño\(G_{p}(\delta) ?\) Si este es el caso, decimos que\(f\) es continuo en\(p .\) Más precisamente, formulamos la siguiente definición.
Se dice que una función\(f : A \rightarrow\left(T, \rho^{\prime}\right),\) con\(A \subseteq(S, \rho),\) es continua en\(p\) iff\(p \in A\) y, además, para cada uno\(\varepsilon>0\) (no importa cuán pequeña sea) hay\(\delta>0\) tal que\(\rho^{\prime}(f(x), f(p))<\varepsilon\) para todos los símbolos\(x \in A \cap G_{p}(\delta) .\) In,
\[(\forall \varepsilon>0)(\exists \delta>0)\left(\forall x \in A \cap G_{p}(\delta)\right)\left\{\begin{array}{l}{\rho^{\prime}(f(x), f(p))<\varepsilon, \text { or }} \\ {f(x) \in G_{f(p)}(\varepsilon)}\end{array}\right.\]
Si\((1)\) falla, decimos que\(f\) es discontinuo en\(p\) y llamamos a\(p\) un punto de discontinuidad de\(f .\) Este también es el caso si\(p \notin A\) (ya que no\(f(p)\) está definido).
Si se\((1)\) sostiene por cada p en un conjunto\(B \subseteq A,\) decimos que\(f\) es continuo en\(B .\) Si este es el caso\(B=A,\) porque simplemente decimos que\(f\) es continuo.
A veces preferimos mantenernos\(x\) cerca\(p\) pero diferentes de Luego\(p .\)\(G_{p}(\delta)\) reemplazamos\((1)\) por el conjunto\(G_{p}(\delta)-\{p\},\) es decir, el globo sin su centro, denotado\(G_{\neg p}(\delta)\) y llamado el\(\delta\) -globo eliminado sobre\(p .\) Esto es incluso necesario si\(p \notin D_{f}\). Sustituyendo\(f(p)\) en\((1)\) por algunos entonces\(q \in T,\) nos llevan a la siguiente definición.
Dado\(f : A \rightarrow\left(T, \rho^{\prime}\right), A \subseteq(S, \rho), p \in S,\) y\(q \in T,\) decimos que\(f(x)\) tiende a\(q\) como\(x\) tiende a\(p(f(x) \rightarrow q \text { as } x \rightarrow p)\) iff para cada uno\(\varepsilon>0\) hay\(\delta>0\) tal que\(\rho^{\prime}(f(x), q)<\varepsilon\) para todos\(x \in A \cap G_{\neg p}(\delta) .\) En símbolos,
\[(\forall \varepsilon>0)(\exists \delta>0)\left(\forall x \in A \cap G_{\neg p}(\delta)\right) \quad\left\{\begin{array}{l}{\rho^{\prime}(f(x), q)<\varepsilon, \text { i.e. }} \\ {f(x) \in G_{q}(\varepsilon)}\end{array}\right.\]
Esto significa que\(f(x)\) está\(\varepsilon\) -cerca de\(q\) cuando\(x\) está\(\delta\) -cerca de\(p\) y\(x \neq p\).
Si las\((2)\) retenciones para algunos\(q,\) llamamos\(q\) límite de\(f\) al Puede que no\(p .\) haya tal\(q\). Entonces decimos que no\(f\) tiene límite en\(p,\) o que este límite no existe. Si solo hay uno de esos\(q(\text { for a given } p),\) escribimos\(q=\lim _{x \rightarrow p} f(x) .\)
Nota 1. La fórmula (2) sostiene “vacuamente” (ver Capítulo 1,8 §§1-3, observación final) si\(A \cap G_{\neg p}(\delta)=\emptyset\) para algunos\(\delta>0 .\) Entonces cualquiera\(q \in T\) es un límite en\(p,\) entonces existe un límite pero no es único. (Descartamos el caso donde\(T\) es un singleton.)
Nota 2. Sin embargo, la singularidad está asegurada si\(A \cap G_{\neg p}(\delta) \neq \emptyset\) para todos\(\delta>0,\) como demostramos a continuación.
Observe que por el Corolario 6 del Capítulo 3, §14, el conjunto se\(A\) agrupa en\(p\) iff
\[(\forall \delta>0) \quad A \cap G_{\neg p}(\delta) \neq \emptyset . \quad(\text { Explain! })\]
Así tenemos el siguiente corolario.
Si\(A\) los clústeres\(p\) en in\((S, \rho),\) entonces una función\(f : A \rightarrow\left(T, p^{\prime}\right)\) puede tener como máximo un límite en\(p ;\) i.e.
\[\lim _{x \rightarrow p} f(x) \text{ is unique (if it exists).}\]
En particular, esto se sostiene si\(A \supseteq(a, b) \subset E^{1}(a<b)\) y\(p \in[a, b]\).
- Prueba
-
Supongamos que\(f\) tiene\(t w o\) límites,\(q\) y\(r,\) en la propiedad\(p .\) By the Hausdorff,
\[G_{q}(\varepsilon) \cap G_{r}(\varepsilon)=\emptyset \quad \text{ for some } \varepsilon>0.\]
También, por\((2),\) hay\(\delta^{\prime}, \delta^{\prime \prime}>0\) tales que
\[\begin{array}{ll}{\left(\forall x \in A \cap G_{\neg p}\left(\delta^{\prime}\right)\right)} & {f(x) \in G_{q}(\varepsilon) \text { and }} \\ {\left(\forall x \in A \cap G_{\neg p}\left(\delta^{\prime \prime}\right)\right)} & {f(x) \in G_{r}(\varepsilon)}\end{array}\]
Let\(\delta=\min \left(\delta^{\prime}, \delta^{\prime \prime}\right) .\) Entonces para\(x \in A \cap G_{\neg p}(\delta), f(x)\) está en ambos\(G_{q}(\varepsilon)\) y\(G_{r}(\varepsilon)\), y tal\(x\) existe ya que\(A \cap G_{\neg p}(\delta) \neq \emptyset\) por suposición.
Pero esto es imposible ya que\(G_{q}(\varepsilon) \cap G_{r}(\varepsilon)=\emptyset\)\((\text { a contradiction!). } \square\)
Para intervalos, ver Capítulo 3, §14, Ejemplo (\(\mathrm{h} )\).
\(f\)es continuo en\(p\left(p \in D_{f}\right)\) iff\(f(x) \rightarrow f(p)\) como\(x \rightarrow p\).
- Prueba
-
La prueba directa de las definiciones se deja al lector.
Nota 3. En fórmula\((2),\) excluimos el caso\(x=p\) asumiendo que\(x \in A \cap G_{\neg p}(\delta) .\) Esto hace que el comportamiento de por\(p\) sí\(f\) mismo sea irrelevante. Así para la existencia de un límite\(q\) en\(p,\) ello no importa si\(p \in D_{f}\) o si\(f(p)=q .\) Pero ambas condiciones se requieren para la continuidad en\(p\) (ver Corolario 2 y Definición 1\()\).
Nota 4. Observe que si\((1)\) o\((2)\) sostiene para algunos\(\delta,\) ciertamente sostiene para cualquier\(\delta^{\prime} \leq \delta .\) Así que siempre podemos elegir\(\delta\) lo pequeño que queramos. Además, como\(x\) se limita a\(G_{p}(\delta),\) nosotros podemos despreciar, o cambiar a voluntad, los valores de función\(f(x)\) para\(x \notin G_{p}(\delta)\) (“carácter local de la noción límite”).
II. Límites en E*. Si\(S\) o\(T\) es\(E^{*}\left(\text { or } E^{1}\right),\) podemos dejar\(x \rightarrow \pm \infty\) o\(f(x) \rightarrow \pm \infty .\) Para una definición precisa, reescribimos\((2)\) en términos de\(globes\)\(G_{p}\) y\(G_{q} :\)
\[\left(\forall G_{q}\right)\left(\exists G_{p}\right)\left(\forall x \in A \cap G_{\neg p}\right) \quad f(x) \in G_{q}.\]
Esto tiene sentido también si\(p=\pm \infty\) o Solo\(q=\pm \infty .\) tenemos que usar nuestras convenciones en cuanto a\(G_{ \pm \infty},\) o la métrica\(\rho^{\prime}\) para\(E^{*},\) como se explica en el Capítulo 3, §11.
Por ejemplo, considere
\[^{\prime \prime}f(x) \rightarrow q \text{ as } x \rightarrow+\infty^{\prime \prime}\left(A \subseteq S=E^{*}, p=+\infty, q \in\left(T, \rho^{\prime}\right)\right).\]
Aquí\(G_{p}\) tiene la forma\((a,+\infty], a \in E^{1},\) y\(G_{\neg p}=(a,+\infty),\) mientras\(G_{q}=G_{q}(\varepsilon)\), como de costumbre. Observando eso\(x \in G_{\neg p}\) significa que\(x>a\left(x \in E^{1}\right),\) podemos reescribir\(\left(2^{\prime}\right)\) como
\[(\forall \varepsilon>0)\left(\exists a \in E^{1}\right)(\forall x \in A | x>a) \quad f(x) \in G_{q}(\varepsilon), \text{ or } \rho^{\prime}(f(x), q)<\varepsilon.\]
Esto significa que\(f(x)\) se vuelve arbitrariamente cercano a\(q\) por lo grande\(x(x>a)\).
A continuación considere\(^{4} f(x) \rightarrow+\infty\) como\(x \rightarrow-\infty\) "Aquí\(G_{\neg p}=(-\infty, a)\) y\(G_{q}=(b,+\infty] .\) Así\(\left(2^{\prime}\right)\) rendimientos de fórmula (con\(S=T=E^{*},\) y\(x\) variando sobre\(E^{\mathrm{i}} )\)
\[\left(\forall b \in E^{1}\right)\left(\exists a \in E^{1}\right)(\forall x \in A | x<a) \quad f(x)>b;\]
de manera similar en otros casos, que dejamos al lector.
Nota 5. En\((3),\) podemos tomar\(A=N\) (los naturales). Luego\(f : N \rightarrow\left(T, \rho^{\prime}\right)\) es una secuencia en\(T .\) Escritura\(m\) para\(x,\) conjunto\(u_{m}=f(m)\) y\(a=k \in N\) para obtener
\[(\forall \varepsilon>0)(\exists k)(\forall m>k) \quad u_{m} \in G_{q}(\varepsilon) ; \text{ i.e., } \rho^{\prime}\left(u_{m}, q\right)<\varepsilon.\]
Esto coincide con nuestra definición del límite\(q\) de una secuencia\(\left\{u_{m}\right\}\) (ver Capítulo 3, §14). Así, los límites de secuencias son un caso especial de límites de función. Los teoremas sobre secuencias se pueden obtener de aquellos sobre funciones simplemente\(f : A \rightarrow\left(T, \rho^{\prime}\right)\) tomando\(A=N\) y\(S=E^{*}\) como arriba.
Nota 6. Fórmulas\((3)\) y tienen\((4)\) sentido también si\(S=E^{1}\) (respectivamente,\(S=T=E^{1} )\) ya que no implican ninguna mención de\(\pm \infty .\) Vamos a utilizar tales fórmulas también para funciones\(f : A \rightarrow T,\) con\(A \subseteq S \subseteq E^{1}\) o\(T \subseteq E^{1},\) según sea el caso.
III. Límites Relativos y Continuidad. A veces el resultado deseado\((1)\) o\((2)\) no se sostiene en su totalidad, sino solo con\(A\) reemplazado por un conjunto más pequeño\(B \subseteq A\). Así podemos tener
\[(\forall \varepsilon>0)(\exists \delta>0)\left(\forall x \in B \cap G_{\neg p}(\delta)\right) \quad f(x) \in G_{q}(\varepsilon).\]
En este caso, llamamos\(q\) un límite relativo de\(f\) al\(p\) más\(B\) y escribimos
\["f(x) \rightarrow q \text{ as } x \rightarrow p \text{ over } B"\]
o
\[\lim _{x \rightarrow p, x \in B} f(x)=q \quad(\text { if } q \text { is unique });\]
\(B\)se llama el camino sobre el que\(x\) tiende a\(p .\) Si, además,\(p \in D_{f}\) y\(q=f(p),\) decimos que\(f\) es relativamente continuo en\(p\) más\(B ;\) entonces se\((1)\) sostiene con\(A\) reemplazado por\(B\). Nuevamente, si esto se sostiene para cada\(p \in B,\) decimos que\(f\) es relativamente continuo en\(B .\) Claramente, si\(B=A=D_{f},\) esto arroja límites ordinarios (no relativos) y continuidad. Así, los límites relativos y la continuidad son más generales.
Tenga en cuenta que para los límites sobre una ruta\(B, x\) se elige de\(B\) o\(B-\{p\}\) solo. Así el comportamiento del\(f\) exterior\(B\) se vuelve irrelevante, y así podemos redefinir arbitrariamente\(f\) en\(-B .\) Por ejemplo, si\(p \notin B\) pero\(\lim _{x \rightarrow p, x \in B} f(x)=q\) existe, podemos definir haciendo\(f(p)=q,\) así\(f\) relativamente continuo en También\(p(\text { over } B) .\) podemos reemplazar\((S, \rho)\) por \((B, \rho)(\text { if } p \in B),\)o restringir\(f\) a\(B,\) es decir, reemplazar\(f\) por la función\(g : B \rightarrow\left(T, \rho^{\prime}\right)\) definida por\(g(x)=f(x)\) for\(x \in B\) (brevemente,\(g=f\) on\(B )\).
Un caso particularmente importante es
\[A \subseteq S \subseteq E^{*}, \text{ e.g., } S=E^{1}.\]
Entonces las desigualdades se definen en\(S,\) para que podamos tomar
\[B=\{x \in A | x<p\} \text{ (points in } A, \text{ preceding } p).\]
Luego, escribiendo\(G_{q}\) para\(G_{q}(\varepsilon)\) y\(a=p-\delta,\) obtenemos de la fórmula\((2)\)
\[\left(\forall G_{q}\right)(\exists a<p)(\forall x \in A | a<x<p) \quad f(x) \in G_{q}.\]
Si se\((5)\) mantiene, llamamos a\(q\) un límite izquierdo de\(f\) at\(p\) y escribimos
\["f(x) \rightarrow q \text{ as } x \rightarrow p^{-}" \quad\left(" x \text { tends to } p \text{ from the left}^{\prime}\right).\]
Si, además,\(q=f(p),\) decimos que\(f\) se deja continuo en\(p .\) Similarmente, tomando
\[B=\{x \in A | x>p\},\]
obtenemos los límites correctos y la continuidad. Escribimos
\[f(x) \rightarrow q \text{ as } x \rightarrow p^{+}\]
iff\(q\) es un límite derecho de\(f\) at\(p,\) i.e., si se\((5)\) mantiene con todas las desigualdades invertidas.
Si el conjunto\(B\) en cuestión agrupa en\(p,\) el límite relativo (si lo hay) es único. Luego denotamos el límite izquierdo y derecho, respectivamente, por\(f\left(p^{-}\right)\) y\(f\left(p^{+}\right),\) y escribimos
\[\lim _{x \rightarrow p^{-}} f(x)=f\left(p^{-}\right) \text{ and } \lim _{x \rightarrow p^{+}} f(x)=f\left(p^{+}\right).\]
Con la notación anterior, si\(f(x) \rightarrow q\) como\(x \rightarrow p\) sobre un camino\(B,\) y también sobre\(D,\) entonces\(f(x) \rightarrow q\) como\(x \rightarrow p\) sobre\(B \cup D\).
De ahí si\(D_{f} \subseteq E^{*}\) y\(p \in E^{*},\) tenemos
\[q=\lim _{x \rightarrow p} f(x) \text{ iff } q=f\left(p^{-}\right)=f\left(p^{+}\right) . \quad(\text { Exercise! })\]
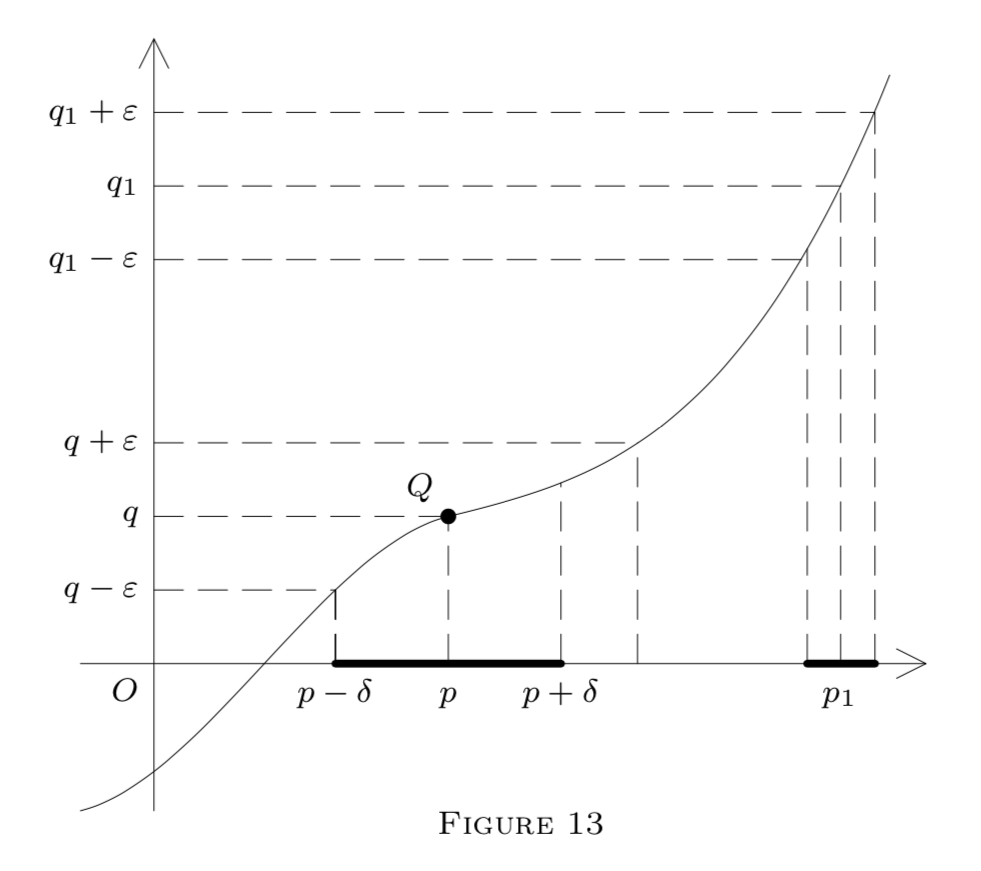
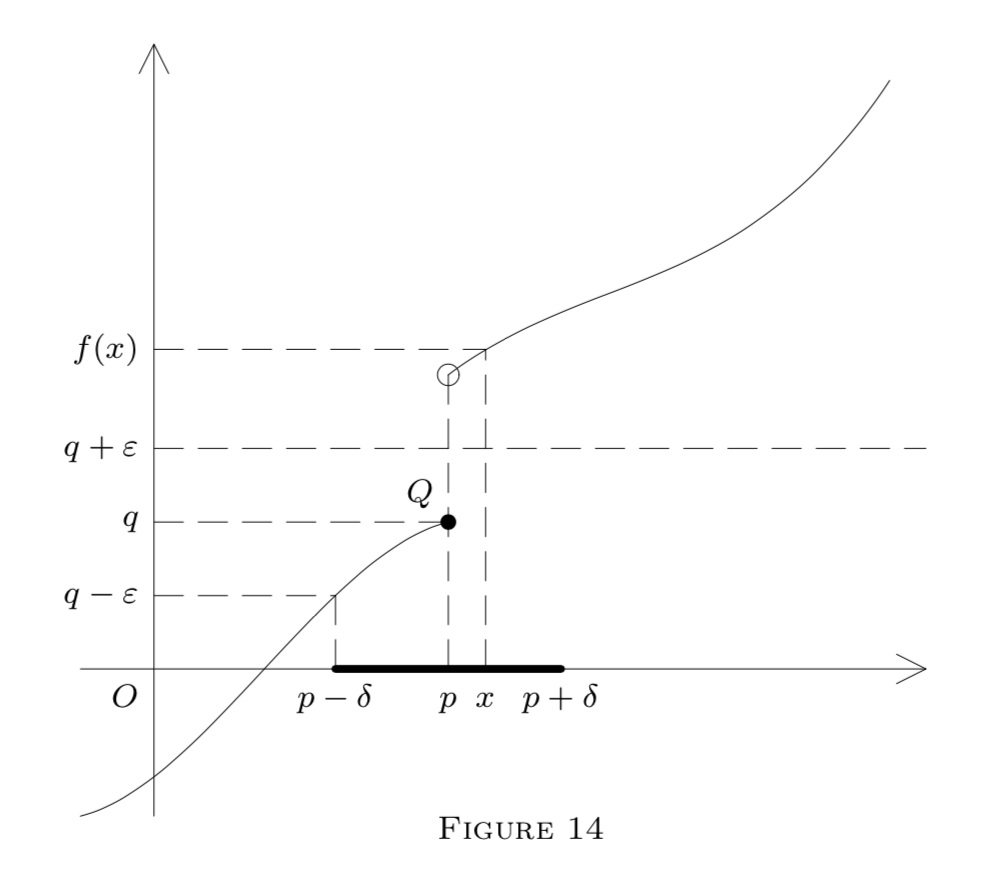
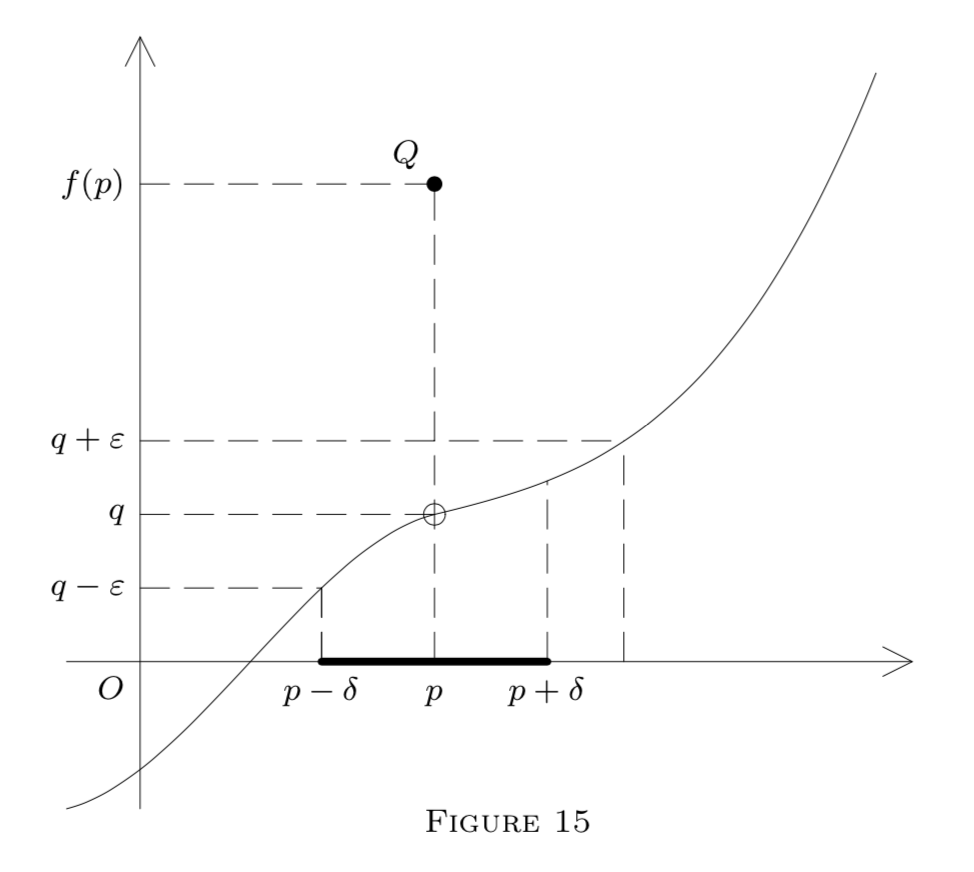
Ahora ilustramos nuestras definiciones mediante un diagrama en la\(E^{2}\) representación de una función\(f : E^{1} \rightarrow E^{1}\) por su gráfica, es decir, puntos\((x, y)\) tales que\(y=f(x)\).
Aquí
\[G_{q}(\varepsilon)=(q-\varepsilon, q+\varepsilon)\]
es un intervalo en el\(y\) eje. Las líneas punteadas muestran cómo construir un intervalo
\[(p-\delta, p+\delta)=G_{p}\]
en el\(x\) eje -eje, satisfaciendo fórmula\((1)\) en la Figura\(13,\) fórmulas\((5)\) y\((6)\) en Figura\(14,\) o fórmula\((2)\) en Figura\(15 .\) El punto\(Q\) en cada diagrama pertenece a la gráfica; es decir,\(Q=(p, f(p)) .\) En la Figura\(13, f\) es continuo en\(p(\text { and also at }\) \(p_{1}\)). Sin embargo, solo es continuo a la izquierda\(p\) en la Figura\(14,\) y es discontinuo\(p\) en la Figura\(15,\) aunque\(f\left(p^{-}\right)\) y\(f\left(p^{+}\right)\) existe. (¿Por qué?)
(a) Dejar\(f : A \rightarrow T\) ser constante en\(B \subseteq A ;\) i.e.
\[f(x)=q \text{ for a fixed } q \in T \text{ and all } x \in B.\]
Entonces\(f\) es relativamente continuo encendido\(B,\) y\(f(x) \rightarrow q\) como\(x \rightarrow p\) más\(B,\) en cada uno\(p .\) (Dado\(\varepsilon>0,\) tomar una arbitraria\(\delta>0\). Entonces
\[\left(\forall x \in B \cap G_{\neg p}(\delta)\right) \quad f(x)=q \in G_{q}(\varepsilon),\]
según se requiera; de manera similar para la continuidad.)
(b) Dejar\(f\) ser el mapa de\(i\) dentidad en\(A \subset(S, \rho) ;\) i.e.
\[(\forall x \in A) \quad f(x)=x.\]
Entonces, dado\(\varepsilon>0,\) toma\(\delta=\varepsilon\) para obtener, para\(p \in A\),
\[\left(\forall x \in A \cap G_{p}(\delta)\right) \quad \rho(f(x), f(p))=\rho(x, p)<\delta=\varepsilon.\]
Por lo tanto, por\((1), f\) es continuo en cualquier\(p \in A,\) por lo tanto en\(A\).
(c) Definir\(f : E^{1} \rightarrow E^{1}\) por
\[f(x)=1 \text{ if } x \text{ is rational, and } f(x)=0 \text{ otherwise.}\]
(Esta es la función Dirichlet, así llamada así en honor a Johann Peter Gustav Lejeune Dirichlet.)
No importa lo pequeño\(\delta\) que sea, el globo
\[G_{p}(\delta)=(p-\delta, p+\delta)\]
(incluso el globo eliminado) contiene tanto racionales como irracionales. Así como\(x\) varía sobre\(G_{\neg p}(\delta), f(x)\) toma ambos valores, 0 y\(1,\) muchas veces y así sale de cualquiera\(G_{q}(\varepsilon),\) con\(q \in E^{1}, \varepsilon<\frac{1}{2}\).
De ahí que para cualquier\(q, p \in E^{1},\) fórmula\((2)\) falle si tomamos\(\varepsilon=\frac{1}{4},\) digamos. Así no\(f\) tiene límite en ningún\(p \in E^{1}\) y por lo tanto es discontinuo en todas partes! Sin embargo,\(f\) es relativamente continuo en el conjunto\(R\) de todos los racionales por Ejemplo\((\mathrm{a})\).
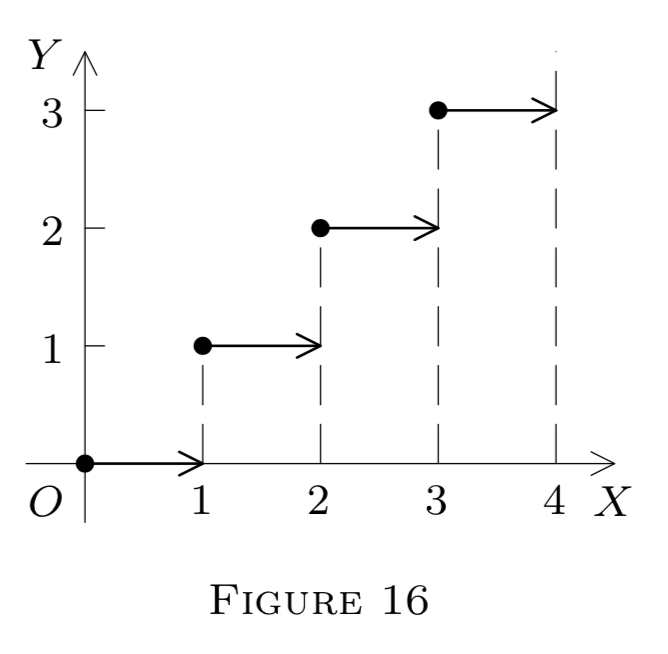
d) Definir\(f : E^{1} \rightarrow E^{1}\) por
\[f(x)=[x](=\text { the integral part of } x ; \text { see Chapter } 2, §10).\]
Así\(f(x)=0\) para\(x \in[0,1), f(x)=1\) para\(x \in[1,2),\) etc. Entonces\(f\) es discontinuo en\(p\) si\(p\) es un número entero (¿por qué?) pero continuo en cualquier otro\(p\left(\text { restrict } f \text { to a small } G_{p}(\delta) \text { so as to make it constant) }\right.\)
Sin embargo, existen límites izquierdo y derecho en cada uno\(p \in E^{1},\) aunque\(p=\)\(n(\text { an integer }) .\) De hecho,
\[f(x)=n, x \in(n, n+1)\]
y
\[f(x)=n-1, x \in(n-1, n),\]
por lo tanto,\(f\left(n^{+}\right)=n\) y\(f\left(n^{-}\right)=\)\(n-1 ; f\) es correcto continuo en\(E^{1} .\) Ver Figura\(16 .\)
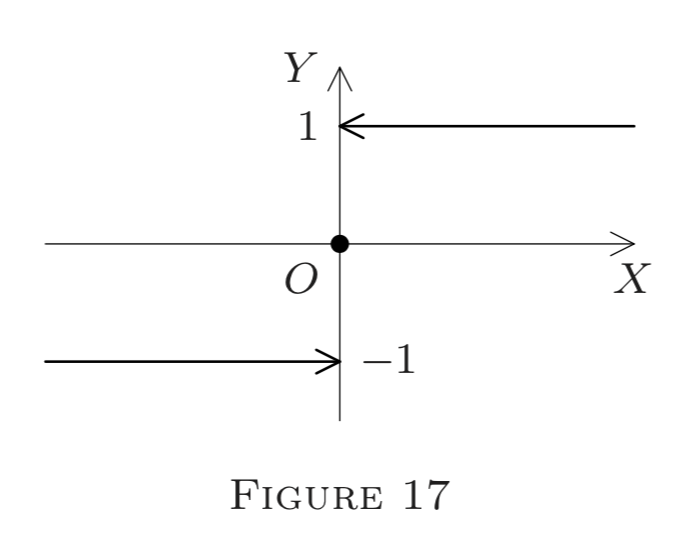
e) Definir\(f : E^{1} \rightarrow E^{1}\) por
\[f(x)=\frac{x}{|x|} \text{ if } x \neq 0, \text{ and } f(0)=0.\]
(Esta es la llamada función signum, a menudo denotada por sgn.)
Entonces (Figura 17\()\)
\[f(x)=-1 \text{ if } x<0\]
y
\[f(x)=1 \text{ if } x>0.\]
Así, como en (d), inferimos que\(f\) es discontinuo en\(0,\) pero continuo en cada\(p \neq 0 .\) También,\(f\left(0^{+}\right)=1\) y\(f\left(0^{-}\right)=-1 .\) Redefiniendo\(f(0)=1\) o\(f(0)=-1,\) podemos hacer\(f\) derecha (respectivamente, izquierda) continua en\(0,\) pero no ambas.
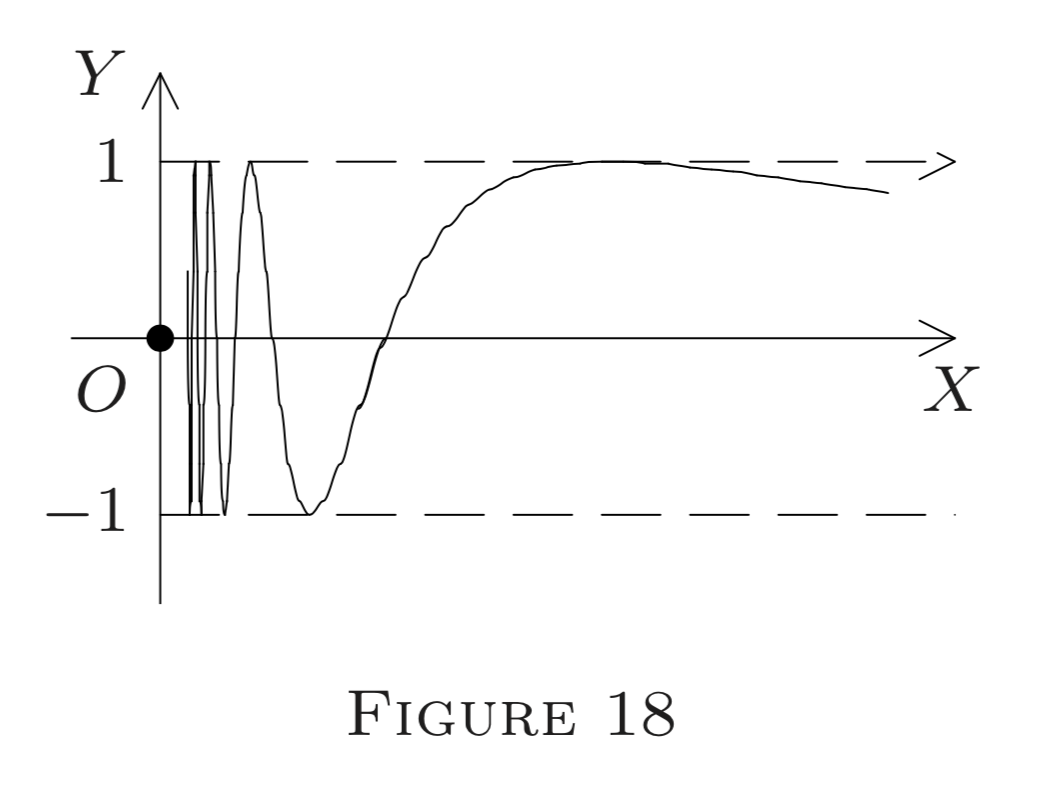
(f) Definir\(f : E^{1} \rightarrow E^{1}\) por (ver Figura 18\()\)
\[f(x)=\sin \frac{1}{x} \text{ if } x \neq 0, \text{ and } f(0)=0.\]
Cualquier globo\(G_{0}(\delta)\) alrededor de 0 contiene puntos en los que así\(f(x)=1,\) como aquellos en los que\(f(x)=-1\) o\(f(x)=0\) (tomar\(x=2 /(n \pi)\) para enteros grandes\(n )\); de hecho, la gráfica “oscila” infinitamente muchas veces entre\(-1\) y\(1 .\) Así por el mismo argumento que en no\((\mathrm{c}), f\) tiene límite en 0 (ni siquiera un límite izquierdo o derecho) y por lo tanto es discontinuo en\(0 .\) Ningún intento de redefinir\(f\) en 0 puede restaurar incluso la continuidad izquierda o derecha, y mucho menos la continuidad ordinaria, en\(0 .\)
g) Definir\(f : E^{2} \rightarrow E^{1} \mathrm{by}\)
\[f(\overline{0})=0 \text{ and } f(\overline{x})=\frac{x_{1} x_{2}}{x_{1}^{2}+x_{2}^{2}} \text{ if } \overline{x}=\left(x_{1}, x_{2}\right) \neq \overline{0}.\]
Dejar\(B\) ser cualquier línea\(E^{2}\) a través\(\overline{0},\) dada paramétricamente por
\[\overline{x}=t \vec{u}, \quad t \in E^{1}, \vec{u} \text{ fixed (see Chapter 3, §§4-6 ),}\]
así\(x_{1}=t u_{1}\) y\(x_{2}=t u_{2} .\) Como se ve fácilmente, para\(\overline{x} \in B, f(\overline{x})=f(\overline{u})\) (constante) si\(\overline{x} \neq \overline{0} .\) Por lo tanto
\[\left(\forall \overline{x} \in B \cap G_{\neg \overline{0}}(\delta)\right) \quad f(\overline{x})=f(\overline{u}),\]
es decir,\(\rho(f(\overline{x}), f(\overline{u}))=0<\varepsilon,\) para cualquier\(\varepsilon>0\) globo eliminado sobre\(\overline{0}\).
Para\(\left(2^{\prime}\right),\) entonces,\(f(\overline{x}) \rightarrow f(\overline{u})\) como\(\overline{x} \rightarrow \overline{0}\) sobre el camino\(B .\) Así\(f\) tiene un límite\(f(\overline{u})\) relativo\(\overline{0},\) sobre cualquier línea\(\overline{x}=t \overline{u},\) pero este límite es diferente para varias opciones de\(\overline{u},\) es decir, para diferentes líneas a través de\(\overline{0} .\) Sin límite ordinario en\(\overline{0}\) existe (¿por qué?) ; ni siquiera\(f\) es relativamente continuo\(\overline{0}\) sobre la línea a\(\overline{x}=t \vec{u}\) menos que\(f(\overline{u})=0\) (que es el caso solo si la línea es uno de los ejes de coordenadas (¿por qué?)).


