5.10: Condición Suficiente de Integrabilidad. Funciones reguladas
- Page ID
- 113982
This page is a draft and is under active development.
En esta sección, determinaremos una gran familia de funciones que sí tienen antiderivados. Primero, damos una definición general, válida para cualquier espacio de rango\((T, p)\) (no necesariamente\(E).\) El espacio de dominio permanece\(E^{1}\).
\(f : E^{1} \rightarrow(T, p)\)Se dice que una función está regulada en un intervalo\(I \subseteq E^{1},\) con puntos finales\(a<b,\) iff los límites\(f\left(p^{-}\right)\) y\(f\left(p^{+}\right),\) que\(\pm \infty,\) no existan en cada uno\(p \in I.\) Sin embargo, en los puntos finales\(a, b,\) si en solo\(I,\) requerimos\(f\left(a^{+}\right)\) y\(f\left(b^{-}\right)\) existimos.
(a) Si\(f\) es relativamente continuo y finito sobre\(I,\) él está regulado.
(b) Toda función monótona real está regulada (ver Capítulo 4, §5, Teorema 1).
(c) Si\(f : E^{1} \rightarrow E^{n}\left(^{*} C^{n}\right)\) tiene variación acotada sobre\(I,\) ella está regulada (§7, Teorema 4).
d) La función característica de un conjunto\(B,\) denotado\(C_{B},\) se define por
\[C_{B}(x)=1 \text { if } x \in B \text { and } C_{B}=0 \text { on }-B.\]
Para cualquier intervalo\(J \subseteq E^{1}, C_{J}\) se regula en\(E^{1}\).
(e) Una función\(f\) se denomina una función de paso en\(I\) iff se\(I\) puede representar como la unión,\(I=\bigcup_{k} I_{k},\) de una secuencia de intervalos disjuntos\(I_{k}\) tal que\(f\) es constante y\(\neq \pm \infty\) en cada uno\(I_{k}\). Tenga en cuenta que algunos\(I_{k}\) pueden ser singletons,\(\{p\}.\)
Si el número del\(I_{k}\) es finito, llamamos a\(f\) una función de paso simple.
Cuando el espacio de rango\(T\) es\(E,\) podemos dar la siguiente definición alternativa conveniente. Si, digamos,\(f=a_{k} \neq \pm \infty\) en\(I_{k},\) entonces
\[f=\sum_{k} a_{k} C_{I_{k}} \quad \text { on } I,\]
donde\(C_{I_{k}}\) es como en la letra d). Tenga en cuenta que\(\sum_{k} a_{k} C_{I_{k}}(x)\) siempre existe para disjuntos\(I_{k}.\) (¿Por qué?)
Cada función de paso simple está regulada. (¿Por qué?)
Deje que las funciones\(f, g, h\) sean reales o complejas (o que\(f, g\) sean valoradas vectoriales y valorizadas h escalares).
Si están regulados en\(I,\) lo son\(f \pm g, f h,\) y también\(|f|;\) lo es\(f / h\) si\(h\) está delimitado lejos de 0 en\(I,\) es decir,\((\exists \varepsilon>0)|h| \geq \varepsilon\) en\(I.\)
- Prueba
-
La prueba, basada en las propiedades límite habituales, se deja al lector.
Vamos a necesitar dos lemmas. Uno es el famoso lema de Heine-Borel.
Si un intervalo cerrado\(A=[a, b]\) en\(E^{1}\) (o\(E^{n})\) está cubierto por conjuntos abiertos,\(G_{i}(i \in I),\) es decir,
\[A \subseteq \bigcup_{i \in I} G_{i},\]
entonces\(A\) puede ser cubierto por un número finito de estos\(G_{i}\).
- Prueba
-
La prueba fue bosquejada en el Problema 10 del Capítulo 4, §6.
Nota 1. Esto falla para intervalos no cerrados\(A.\) Por ejemplo, vamos
\[A=(0,1) \subseteq E^{1} \text { and } G_{n}=\left(\frac{1}{n}, 1\right).\]
Entonces
\[A=\bigcup_{n=1}^{\infty} G_{n}(\text { verify! }), \text { but not } A \subseteq \bigcup_{n=1}^{m} G_{n}\]
para cualquier finito\(m.\) (¿Por qué?)
El lema también falla para sets no abiertos Por\(G_{i}.\) ejemplo, portada\(A\) por singletons ¡\(\{x\}, x \in A.\)Entonces ninguno de los se\(\{x\}\) puede dejar caer!
Si\(f : E^{1} \rightarrow T\) se regula una función\(I=[a, b],\), entonces\(f\) puede aproximarse uniformemente mediante funciones de paso simples en\(I.\)
Es decir, para cualquiera\(\varepsilon>0,\) hay una función de paso simple\(g,\) con\(\rho(f, g) \leq \varepsilon\) on de\(I;\) ahí
\[\sup _{x \in I} \rho(f(x), g(x)) \leq \varepsilon.\]
- Prueba
-
Por suposición,\(f\left(p^{-}\right)\) existe para cada uno\(p \in(a, b],\) y\(f\left(p^{+}\right)\) existe para\(p \in[a, b),\) todos finitos.
Así, dado\(\varepsilon>0\) y cualquiera que\(p \in I,\) haya\(G_{p}(\delta\))\((\delta\) dependiendo de\(p\)) tal que\(\rho(f(x), r)<\varepsilon\) cuando\(r=f\left(p^{-}\right)\)\(x \in(p-\delta, p),\) y\(\rho(f(x), s)<\varepsilon\) cuando\(s=f\left(p^{+}\right)\) y\(x \in(p, p+\delta); x \in I\)
Elegimos tal\(G_{p}(\delta)\) para cada\(p \in I.\) Entonces los globos abiertos\(G_{p}=G_{p}(\delta)\) cubren el intervalo cerrado\(I=[a, b],\) así que por Lema 1,\(I\) está cubierto por un número finito de tales globos, digamos,
\[I \subseteq \bigcup_{k=1}^{n} G_{p_{k}}\left(\delta_{k}\right), \quad a \in G_{p_{1}}, a \leq p_{1}<p_{2}<\cdots<p_{n} \leq b.\]
Ahora definimos la función step\(g\) on de la\(I\) siguiente manera.
Si\(x=p_{k},\) ponemos
\[g(x)=f\left(p_{k}\right), \quad k=1,2, \ldots, \text{ } n.\]
Si\(x \in\left[a, p_{1}\right),\) entonces
\[g(x)=f\left(p_{1}^{-}\right).\]
Si\(x \in\left(p_{1}, p_{1}+\delta_{1}\right),\) entonces
\[g(x)=f\left(p_{1}^{+}\right).\]
De manera más general, si\(x\) está en\(G_{\neg p_{k}}\left(\delta_{k}\right)\) pero en ninguna de las\(G_{p_{i}}\left(\delta_{i}\right), i<k,\) ponemos
\[g(x)=f\left(p_{k}^{-}\right) \quad \text { if } x<p_{k}\]
y
\[g(x)=f\left(p_{k}^{+}\right) \quad \text { if } x>p_{k}.\]
Luego por construcción,\(\rho(f, g)<\varepsilon\) en cada de\(G_{p_{k}},\) ahí en\(I. \quad \square\)
*Nota 2. Si\(T\) está completo, podemos decir más:\(f\) se regula en\(I=[a, b]\) iff\(f\) se aproxima uniformemente mediante simples funciones de paso en\(I\). (Ver Problema 2.)
Si\(f : E^{1} \rightarrow E\) se regula en un intervalo\(I \subseteq E^{1}\) y si\(E\) está completo, entonces\(\int f\) existe en\(I,\) exacto en cada punto de continuidad de\(f\) in\(I^{0}\).
En particular, todos los mapas continuos\(f : E^{1} \rightarrow E^{n}\left(^{*} C^{n}\right)\) tienen primitivas exactas.
- Prueba
-
En vista del Problema 14 del §5, basta con considerar intervalos cerrados.
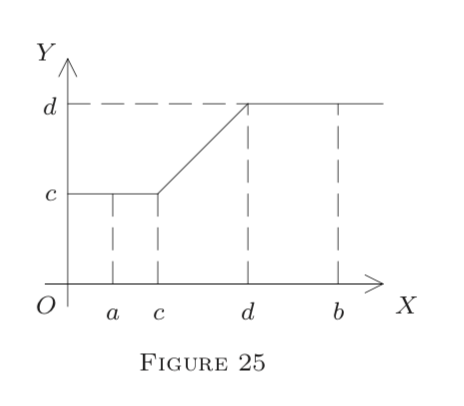
Así dejar\(I=[a, b], a<b,\) entrar\(E^{1}.\) Supongamos primero que\(f\) es la función característica\(C_{J}\) de un subintervalo\(J \subseteq I\) con puntos finales\(c\) y\(d\)\((a \leq c \leq d \leq b),\) así\(f=1\) sucesivamente\(J\) y así\(f=0\) sucesivamente Luego\(I-J.\) definimos\(F(x)=x\) on\(J, F=c\) on \([a, c],\)y\(F=d\) en\([d, b]\) (ver Figura 25). Así\(F\) es continuo (¿por qué?) , y\(F^{\prime}=f\) en\(I-\{a, b, c, d\}\) (¿por qué?). De ahí\(F=\int f\) que en\(I;\) i.e., las funciones características son integrables.
Entonces, sin embargo, también lo es cualquier función de paso simple
\[f=\sum_{k=1}^{m} a_{k} C_{I_{k}},\]
por el uso repetido del Corolario 1 en §5.
Por último, dejar\(f\) ser cualquier función regulada en\(I\). Entonces por Lemma 2, para cualquiera\(\varepsilon_{n}=\frac{1}{n},\) hay una función de paso simple\(g_{n}\) tal que
\[\sup _{x \in I}\left|g_{n}(x)-f(x)\right| \leq \frac{1}{n}, \quad n=1,2, \ldots.\]
Como\(\frac{1}{n} \rightarrow 0,\) esto implica que\(g_{n} \rightarrow f\) (uniformemente) en\(I\) (ver Capítulo 4, §12, Teorema 1). También, por lo que se demostró anteriormente, las funciones escalonadas\(g_{n}\) tienen antiderivados, de ahí que así lo ha hecho\(f\) (Teorema 2 en §9); es decir,\(F=\int f\) existe en\(I,\) como se reivindica. Además,\(\int f\) es exacto en los puntos de continuidad de\(f\) in\(I^{0}\) (Problema 10 en §5). \(\quad \square\)
En vista de la condición suficiente expresada en el Teorema 2, ahora podemos sustituir la suposición "\(\int f\)existe” en nuestros teoremas anteriores por "\(f\)está regulada” (siempre\(E\) que sea completa). Por ejemplo, revisemos ahora los Problemas 7 y 8 en §5.
Dejar\(f : E^{1} \rightarrow E\) (\(E\)completar) y\(g : E^{1} \rightarrow E^{1}\) ser regulado\(I=[a, b],\) con\(g \geq 0\) on\(I.\) Entonces lo siguiente es cierto:
(i) Hay una finita\(c \in E\) (llamada la “media ponderada g de\(f\) on\(I\) “) tal que\(\int_{a}^{b} g f=c \int_{a}^{b} g\).
(ii) Si\(f,\) también, es real y tiene la propiedad Darboux en\(I,\) entonces\(c=f(q)\) para algunos\(q \in I.\)
- Prueba
-
En efecto, como\(f\) y\(g\) están regulados, así lo es\(g f\) por el Teorema 1. De ahí por Teorema 2,\(\int f\) y\(\int g f\) existir en\(I.\) El resto sigue como en Problemas 7 y 8 de §5. \(\quad \square\)
Supongamos\(f\) y\(g\) son reales,\(f\) es monótona con\(f=\int f^{\prime}\) on\(I,\) y\(g\) se regula en\(I; I=[a, b].\) Entonces
\[\int_{a}^{b} f g=f(a) \int_{a}^{q} g+f(b) \int_{q}^{b} g \text { for some } q \in I.\]
- Prueba
-
Para arreglar ideas, vamos\(f \uparrow;\) i.e.,\(f^{\prime} \geq 0\) en\(I\).
La fórmula\(f=\int f^{\prime}\) significa que\(f\) es relativamente continuo (por lo tanto regulado)\(I\) y diferenciable en\(I-Q\) (\(Q\)contable). Tal y como\(g\) está regulado,
\[\int_{a}^{x} g=G(x)\]
existe en\(I,\) por lo que\(G\) tiene propiedades similares, con\(G(a)=\int_{a}^{a} g=0\).
Por Teoremas 1 y 2,\(\int f G^{\prime}=\int f g\) existe en\(I.\) (¿Por qué?) De ahí por Corolario 5 en §5, también lo hace\(\int G f^{\prime},\) y tenemos
\[\int_{a}^{b} f g=\int_{a}^{b} f G^{\prime}=f(x) G\left.(x)\right|_{a} ^{b}-\int_{a}^{b} G f^{\prime}=f(b) G(b)-\int_{a}^{b} G f^{\prime}.\]
Ahora\(G\) tiene la propiedad Darboux en\(I\) (siendo relativamente continua), y\(f^{\prime} \geq 0.\) también,\(\int G\) y\(\int G f^{\prime}\) existe en\(I.\) Así por Problemas 7 y 8 en §5
\[\int_{a}^{b} G f^{\prime}=G(q) \int_{a}^{b} f^{\prime}=G(q) f\left.(x)\right|_{a} ^{b}, \quad q \in I.\]
Combinando todos, obtenemos el resultado requerido (1) ya que
\[\begin{aligned} \int f g &=f(b) G(b)-\int_{a}^{b} G f^{\prime} \\ &=f(b) G(b)-f(b) G(q)+f(a) G(q) \\ &=f(b) \int_{q}^{b} g+f(a) \int_{a}^{q} g . \quad \square \end{aligned}\]
Concluimos con una aplicación a series infinitas. Dado\(f : E^{1} \rightarrow E,\) definimos
\[\int_{a}^{\infty} f=\lim _{x \rightarrow+\infty} \int_{a}^{x} f \text { and } \int_{-\infty}^{a} f=\lim _{x \rightarrow-\infty} \int_{x}^{a} f\]
si existen estas integrales y límites.
Nosotros decimos eso\(\int_{a}^{\infty} f\) y\(\int_{-\infty}^{a} f\) convergen si existen y son finitos.
Si no\(f : E^{1} \rightarrow E^{1}\) es negativo y no aumenta en\(I=[a,+\infty),\) entonces
\[\int_{a}^{\infty} f \text { converges iff } \sum_{n=1}^{\infty} f(n) \text { does.}\]
- Prueba
-
Como\(f \downarrow, f\) está regulado, así\(\int f\) existe en\(I=[a,+\infty).\) Arreglamos algunos naturales\(k \geq a\) y definimos
\[F(x)=\int_{k}^{x} f \text { for } x \in I.\]
Por Teorema 3 (iii) en §5,\(F \uparrow\) en\(I\). Así, por monotonicidad,
\[\lim _{x \rightarrow+\infty} F(x)=\lim _{x \rightarrow+\infty} \int_{k}^{x} f=\int_{k}^{\infty} f\]
existe en\(E^{*};\) lo que hace\(\int_{a}^{k} f.\) Desde
\[\int_{a}^{x} f=\int_{a}^{k} f+\int_{k}^{x} f,\]
donde\(\int_{a}^{k} f\) es finito por definición, tenemos
\[\int_{a}^{\infty} f<+\infty \text { iff } \int_{k}^{\infty} f<+\infty.\]
Del mismo modo,
\[\sum_{n=1}^{\infty} f(n)<+\infty \quad \text { iff } \sum_{n=k}^{\infty} f(n)<+\infty.\]
Así podemos sustituir "\(a\)" por "”\(k\).”
Let
\[I_{n}=[n, n+1), \quad n=k, k+1, \ldots,\]
y definir funciones de dos pasos,\(g\) y\(h,\) constante en cada\(I_{n},\)
\[h=f(n) \text { and } g=f(n+1) \text { on } I_{n}, n \geq k.\]
Ya que\(f \downarrow,\) tenemos\(g \leq f \leq h\) en todos de\(I_{n},\) ahí en Por\(J=[k,+\infty).\) lo tanto,
\[\int_{k}^{x} g \leq \int_{k}^{x} f \leq \int_{k}^{x} h \text { for } x \in J.\]
Además,
\[\int_{k}^{m} h=\sum_{n=k}^{m-1} \int_{n}^{n+1} h=\sum_{n=k}^{m-1} f(n),\]
desde\(h=f(n)\) (constante) encendido\([n, n+1),\) y así
\[\int_{n}^{n+1} h(x) d x=f(n) \int_{n}^{n+1} 1 d x=f(n) \cdot\left.x\right|_{n} ^{n+1}=f(n)(n+1-n)=f(n).\]
Del mismo modo,
\[\int_{k}^{m} g=\sum_{n=k}^{m-1} f(n+1)=\sum_{n=k+1}^{m} f(n).\]
Así obtenemos
\[\sum_{n=k+1}^{m} f(n)=\int_{k}^{m} g \leq \int_{k}^{m} f \leq \int_{k}^{m} h=\sum_{n=k}^{m-1} f(n),\]
o, dejando\(m \rightarrow \infty\),
\[\sum_{n=k+1}^{\infty} f(n) \leq \int_{k}^{\infty} f \leq \sum_{n=k}^{\infty} f(n).\]
De ahí\(\int_{k}^{\infty} f\) es finito iff\(\sum_{n=1}^{\infty} f(n)\) es, y todo está probado. \(\quad \square\)
f) Considerar la serie hiperarmónica
\[\sum \frac{1}{n^{p}} \quad \text {(Problem 2 of Chapter 4, §13).}\]
Let
\[f(x)=\frac{1}{x^{p}}, \quad x \geq 1.\]
Si\(p=1,\) entonces\(f(x)=1 / x,\) así\(\int_{1}^{x} f=\ln x \rightarrow+\infty\) como\(x \rightarrow+\infty.\) De ahí\(\sum 1 / n\) diverge.
Si\(p \neq 1,\) entonces
\[\int_{1}^{\infty} f=\lim _{x \rightarrow+\infty} \int_{1}^{x} f=\lim _{x \rightarrow+\infty}\left.\frac{x^{1-p}}{1-p}\right|_{1} ^{x},\]
así\(\int_{1}^{\infty} f\) converge o diverge según\(p>1\) o\(p<1,\) y lo mismo se aplica a la serie\(\sum 1 / n^{p}.\)
g) Incluso las funciones no reguladas pueden ser integrables. Tal es la función de Dirichlet (Ejemplo (c) en el Capítulo 4, §1). Explique, utilizando la contabilidad de los racionales.


