5.11: Definiciones Integrales de Algunas Funciones
- Page ID
- 113981
This page is a draft and is under active development.
Por Teorema 2 en §10,\(\int f\) existe en\(I\) cada vez que la función\(f : E^{1} \rightarrow E\) está regulada\(I,\) y\(E\) está completa. Por lo tanto, cada vez que\(f\) se da tal, podemos definir una nueva función\(F\) configurando
\[F=\int_{a}^{x} f\]
on I para algunos\(a \in I.\) Este es un método conveniente para obtener nuevas funciones continuas, diferenciables on\(I-Q\) (\(Q\)contables). Ahora la aplicaremos para obtener nuevas definiciones de algunas funciones previamente definidas de una manera bastante extenuante paso a paso.
I. Funciones logarítmicas y exponenciales. A partir de nuestras definiciones anteriores, probamos que
\[\ln x=\int_{1}^{x} \frac{1}{t} d t, \quad x>0.\]
Ahora queremos tratar esto como una definición de logaritmos. Empezamos por establecer
\[f(t)=\frac{1}{t}, \quad t \in E^{1}, t \neq 0,\]
y\(f(0)=0\).
Entonces\(f\) es continuo\(I=(0,+\infty)\) y\(J=(-\infty, 0),\) así tiene un primitivo exacto encendido\(I\) y\(J\) por separado (no encendido\(E^{1}\)). Por lo tanto, ahora podemos definir la función log on\(I\) por
\[\int_{1}^{x} \frac{1}{t} d t=\log x \text { (also written } \ln x ) \text { for } x>0.\]
Por la definición misma de una primitiva exacta, la función log es continua y diferenciable en\(I=(0,+\infty)\); su derivada on\(I\) es\(f\). Así tenemos de nuevo la fórmula simbólica
\[(\log x)^{\prime}=\frac{1}{x}, \quad x>0.\]
Si\(x<0,\) podemos considerar\(\log (-x).\) Entonces la regla de la cadena (Teorema 3 de §1) rinde
\[(\log (-x))^{\prime}=\frac{1}{x}. \quad \text { (Verify!)}\]
De ahí
\[(\log |x|)^{\prime}=\frac{1}{x} \quad \text { for } x \neq 0.\]
Otras propiedades de logaritmos siguen fácilmente de (1). Los resumimos ahora.
(i)\(\log 1=\int_{1}^{1} \frac{1}{t} d t=0\).
ii)\(\log x<\log y\) cuando sea\(0<x<y\).
iii)\(\lim _{x \rightarrow+\infty} \log x=+\infty\) y\(\lim _{x \rightarrow 0^{+}} \log x=-\infty\).
(iv) El rango de bitácora es todo de\(E^{1}\).
v) Por cualquier situación positiva\(x, y \in E^{1}\),
\[\log (x y)=\log x+\log y \text { and } \log \left(\frac{x}{y}\right)=\log x-\log y.\]
vi)\(\log a^{r}=r \cdot \log a, a>0, r \in N\).
vii)\(\log e=1,\) donde\(e=\lim _{n \rightarrow \infty}\left(1+\frac{1}{n}\right)^{n}\).
- Prueba
-
(ii) Por (2),\((\log x)^{\prime}>0\)\(I=(0,+\infty),\) sucesivamente\(\log x\) va en aumento\(I\).
iii) Por Teorema 5 en §10,
\[\lim _{x \rightarrow+\infty} \log x=\int_{1}^{\infty} \frac{1}{t} d t=+\infty\]
desde
\[\sum_{n=1}^{\infty} \frac{1}{n}=+\infty \quad \text {(Chapter 4, §13, Example (b)).}\]
Por lo tanto, sustituyendo\(y=1 / x,\) obtenemos
\[\lim _{y \rightarrow 0^{+}} \log y=\lim _{x \rightarrow+\infty} \log \frac{1}{x}.\]
Sin embargo, por el Teorema 2 en §5 (sustituyendo\(s=1 / t\)),
\[\log \frac{1}{x}=\int_{1}^{1 / x} \frac{1}{t} d t=-\int_{1}^{x} \frac{1}{s} d s=-\log x.\]
Así
\[\lim _{y \rightarrow 0^{+}} \log y=\lim _{x \rightarrow+\infty} \log \frac{1}{x}=-\lim _{x \rightarrow+\infty} \log x=-\infty\]
según lo reclamado. (También probamos que\(\log \frac{1}{x}=-\log x.\))
(iv) La aserción (iv) sigue ahora por la propiedad Darboux (como en el Capítulo 4, §9, Ejemplo (b)).
(v) Con\(x, y\) fijo, sustituimos\(t=x s\) en
\[\int_{1}^{x y} \frac{1}{t} d t=\log x y\]
y obtener
\[\begin{aligned} \log x y &=\int_{1}^{x y} \frac{1}{t} d t=\int_{1 / x}^{y} \frac{1}{s} d s \\ &=\int_{1 / x}^{1} \frac{1}{s} d s+\int_{1}^{y} \frac{1}{s} d s \\ &=-\log \frac{1}{x}+\log y \\ &=\log x+\log y. \end{aligned}\]
\(y\)Sustituyendo por\(1 / y\) aquí, tenemos
\[\log \frac{x}{y}=\log x+\log \frac{1}{y}=\log x-\log y.\]
Así se demuestra (v), y (vi) sigue por inducción sobre\(r\).
vii) Por continuidad,
\[\log e=\lim _{x \rightarrow e} \log x=\lim _{n \rightarrow \infty} \log \left(1+\frac{1}{n}\right)^{n}=\lim _{n \rightarrow \infty} \frac{\log (1+1 / n)}{1 / n},\]
donde la última igualdad sigue por (vi). Ahora, la regla de L'Hôpital cede
\[\lim _{x \rightarrow 0} \frac{\log (1+x)}{x}=\lim _{x \rightarrow 0} \frac{1}{1+x}=1.\]
Dejando\(x\)\(\frac{1}{n} \rightarrow 0,\) atropellar obtenemos (vii). \(\quad \square\)
Nota 1. En realidad, vi) sostiene para cualquiera\(r \in E^{1},\) con\(a^{r}\) como en el Capítulo 2, §§11-12. Se utilizan las técnicas de esa sección para probarlo primero para racional\(r,\) y luego sigue para todos reales\(r\) por continuidad. Sin embargo, preferimos no usar esto ahora.
A continuación, definimos la función exponencial (“exp”) para que sea la inversa de la función log. Esta función inversa existe; es continua (incluso diferenciable) y estrictamente creciente en su dominio (por el Teorema 3 del Capítulo 4, §9 y Teorema 3 del Capítulo 5, §2) ya que la función log tiene estas propiedades. De\((\log x)^{\prime}=1 / x\) obtenemos, como en 2,
\[(\exp x)^{\prime}=\exp x \quad \text {(cf. §2, Example (B)).}\]
El dominio de lo exponencial es el rango de su inverso, es decir,\(E^{1}\) (cf. Teorema 1 (iv)). Así\(\exp x\) se define para todos\(x \in E^{1}.\) El rango de exp es el dominio de log, es decir,\((0,+\infty).\) De ahí exp\(x>0\) para todos\(x \in E^{1}.\) También, por definición,
\[\begin{aligned} \exp (\log x) &=x \text { for } x>0 \\ \exp 0 &=1 \text { (cf. Theorem } 1(\mathrm{i}) ), \text { and } \\ \exp r &=e^{r} \text { for } r \in N. \end{aligned}\]
En efecto, por el Teorema 1 (vi) y (vii), sigue log\(e^{r}=r \cdot \log e=r.\) De ahí (6). Si se utilizan las definiciones y reglas del Capítulo 2, §§11-12, esta prueba incluso funciona para cualquiera\(r\) por Nota 1. Así nuestra nueva definición de exp concuerda con la antigua.
Nuestro siguiente paso es dar una nueva definición de\(a^{r},\) para cualquier\(a, r \in E^{1}(a>0).\) We set
\[\begin{aligned} a^{r} &=\exp (r \cdot \log a) \text { or } \\ \log a^{r} &=r \cdot \log a \quad\left(r \in E^{1}\right). \end{aligned}\]
En caso\(r \in N\), (8) se convierte en Teorema 1 (vi). Así, para natural,\(r,\) nuestra nueva definición de\(a^{r}\) es consistente con la anterior. También obtenemos, para\(a, b>0\),
\[(a b)^{r}=a^{r} b^{r} ; \quad a^{r s}=\left(a^{r}\right)^{s} ; \quad a^{r+s}=a^{r} a^{s} ; \quad\left(r, s \in E^{1}\right).\]
La prueba es tomando logaritmos. Por ejemplo,
\[\begin{aligned} \log (a b)^{r} &=r \log a b=r(\log a+\log b)=r \cdot \log a+r \cdot \log b \\ &=\log a^{r}+\log b^{r}=\log \left(a^{r} b^{r}\right). \end{aligned}\]
Así, se pueden dar argumentos\((a b)^{r}=a^{r} b^{r}.\) similares para el resto de (9) y otras leyes establecidas en el Capítulo 2, §§11-12.
Ahora podemos definir el exponencial a la base\(a(a>0)\) y su inverso, log\(_{a},\) como antes (ver el ejemplo en el Capítulo 4, §5 y Ejemplo (b) en el Capítulo 4, §9). La diferenciabilidad del primero es ahora inmediata de (7), y el resto sigue como antes.
II. Funciones Trigonométricas. Estos se definirán ahora de manera analítica precisa (no basada en geometría).
Comenzamos con una definición integral de lo que generalmente se llama el valor principal de la función arcoseno,
\[\arcsin x=\int_{0}^{x} \frac{1}{\sqrt{1-t^{2}}} d t.\]
Vamos a denotarlo por\(F(x)\) y establecer
\[f(x)=\frac{1}{\sqrt{1-x^{2}}} \text { on } I=(-1,1).\]
\((F=f=0\)encendido\(E^{1}-I\).) Así por definición,\(F=\int f\) en\(I\).
Tenga en cuenta que\(\int f\) existe y es exacto en\(I\) ya que\(f\) es continuo en\(I.\) Así
\[F^{\prime}(x)=f(x)=\frac{1}{\sqrt{1-x^{2}}}>0 \quad \text {for } x \in I,\]
y así\(F\) está aumentando estrictamente en\(I\). También,\(F(0)=\int_{0}^{0} f=0\).
También definimos el número\(\pi\) estableciendo
\[\frac{\pi}{2}=2 \arcsin \sqrt{\frac{1}{2}}=2 F(c)=2 \int_{0}^{c} f, \quad c=\sqrt{\frac{1}{2}}.\]
Después obtenemos el siguiente teorema.
\(F\)tiene los límites
\[F\left(1^{-}\right)=\frac{\pi}{2} \text { and } F\left(-1^{+}\right)=-\frac{\pi}{2}.\]
Por lo tanto,\(F\) se vuelve relativamente continuo\(\overline{I}=[-1,1]\) si uno establece
\[F(1)=\frac{\pi}{2} \text { and } F(-1)=-\frac{\pi}{2},\]
es decir,
\[\arcsin 1=\frac{\pi}{2} \text { and } \arcsin (-1)=-\frac{\pi}{2}.\]
- Prueba
-
Tenemos
\[F(x)=\int_{0}^{x} f=\int_{0}^{c} f+\int_{c}^{x} f, \quad c=\sqrt{\frac{1}{2}}.\]
Al sustituir\(s=\sqrt{1-t^{2}}\) en la última integral y ambientación, por brevedad,\(y=\)\(\sqrt{1-x^{2}},\) obtenemos
\[\int_{c}^{x} f=\int_{c}^{x} \frac{1}{\sqrt{1-t^{2}}} d t=\int_{y}^{c} \frac{1}{\sqrt{1-s^{2}}} d s=F(c)-F(y). \quad \text {(Verify!)}\]
Ahora como\(x \rightarrow 1^{-},\) tenemos\(y=\sqrt{1-x^{2}} \rightarrow 0,\) y por lo tanto\(F(y) \rightarrow F(0)=0\) (para\(F\) es continuo a 0). Así
\[F\left(1^{-}\right)=\lim _{x \rightarrow 1^{-}} F(x)=\lim _{y \rightarrow 0}\left(\int_{0}^{c} f+\int_{y}^{c} f\right)=\int_{0}^{c} f+F(c)=2 \int_{0}^{c} f=\frac{\pi}{2}.\]
Del mismo modo, uno obtiene\(F\left(-1^{+}\right)=-\pi / 2. \quad \square\)
La función\(F\) como se redefine en el Teorema 2 se denotará por\(F_{0}.\) Es una primitiva de\(f\) en el intervalo cerrado\(\overline{I}\) (exacto en\(I).\) Así\(F_{0}(x)=\int_{0}^{x} f,\)\(-1 \leq x \leq 1,\) y ahora podemos escribir
\[\frac{\pi}{2}=\int_{0}^{1} f \text { and } \pi=\int_{-1}^{0} f+\int_{0}^{1} f=\int_{-1}^{1} f.\]
Nota 2. En el análisis clásico, las últimas integrales son consideradas como las llamadas integrales impropias, es decir, límites de integrales más que integrales propiamente dichas. En nuestra teoría, esto es innecesario ya que\(F_{0}\) es un auténtico primitivo de\(f\) on\(\overline{I}.\)
Para cada entero\(n\) (negativos incluidos), ahora definimos\(F_{n} : E^{1} \rightarrow E^{1}\) por
\[\begin{aligned} F_{n}(x) &=n \pi+(-1)^{n} F_{0}(x) \text { for } x \in \overline{I}=[-1,1] \\ F_{n} &=0 & \text { on }-\overline{I}. \end{aligned}\]
\(F_{n}\)se llama la rama\(n\) th del arcoseno. La Figura 26 muestra los gráficos de\(F_{0}\) y\(F_{1}\) (el de\(F_{1}\) es punteado). Ahora obtenemos el siguiente teorema.
(i) Cada uno\(F_{n}\) es diferenciable\(I=(-1,1)\) y relativamente continuo\(\overline{I}=[-1,1]\).
(ii)\(F_{n}\) está aumentando sobre\(\overline{I}\) si\(n\) es par, y decreciente si\(n\) es impar.
iii)\(F_{n}^{\prime}(x)=\frac{(-1)^{n}}{\sqrt{1-x^{2}}}\) en\(I\).
iv)\(F_{n}(-1)=F_{n-1}(-1)=n \pi-(-1)^{n} \frac{\pi}{2} ; F_{n}(1)=F_{n-1}(1)=n \pi+(-1)^{n} \frac{\pi}{2}\).
- Prueba
-
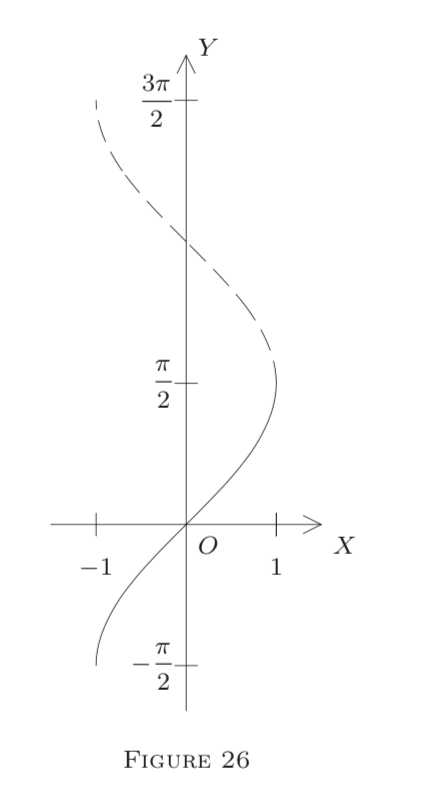
La prueba es obvia a partir de (12) y las propiedades de\(F_{0}.\) Aserción (iv) aseguran que las gráficas de la\(F_{n}\) suman a una curva. Por (ii), cada uno\(F_{n}\) es uno a uno (estrictamente monótona) en\(\overline{I} .\) Así tiene un inverso estrictamente monótona en el intervalo\(\overline{J_{n}}=F_{n}\)\([\![ -1, 1 ]\!] \), es decir, en la\(F_{n}\) -imagen de\(\overline{I}\). Por simplicidad, consideramos solo
\[\overline{J_{0}}=\left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \text { and } J_{1}=\left[\frac{\pi}{2}, \frac{3 \pi}{2}\right],\]
como se muestra en el\(Y\) eje -en la Figura 26. Sobre estos, definimos para\(x \in \overline{J_{0}}\)
\[\sin x=F_{0}^{-1}(x)\]
y
\[\cos x=\sqrt{1-\sin ^{2} x},\]
y para\(x \in \overline{J_{1}}\)
\[\sin x=F_{1}^{-1}(x)\]
y
\[\cos x=-\sqrt{1-\sin ^{2} x}.\]
En el resto de\(E^{1},\) definimos\(\sin x\) y\(\cos x\) periódicamente configurando
\[\sin (x+2 n \pi)=\sin x \text { and } \cos (x+2 n \pi)=\cos x, \quad n=0, \pm 1, \pm 2, \ldots.\]
Nótese que por el Teorema 3 (iv),
\[F_{0}^{-1}\left(\frac{\pi}{2}\right)=F_{1}^{-1}\left(\frac{\pi}{2}\right)=1.\]
Así (13) y (14) ambos rinden\(\sin \pi / 2=1\) para el punto final común\(\pi / 2\) de\(\overline{J_{0}}\) y\(\overline{J_{1}},\) por lo tanto las dos fórmulas son consistentes. También contamos con
\[\sin \left(-\frac{\pi}{2}\right)=\sin \left(\frac{3 \pi}{2}\right)=-1,\]
de acuerdo con (15). Así, las funciones seno y coseno (brevemente,\(s\) y\(c\)) están bien definidas\(E^{1}\).
Las funciones seno y coseno (\(s\)y\(c\)) son diferenciables, por lo tanto continuas, en todas\(E^{1},\) con derivadas\(s^{\prime}=c\) y es\(c^{\prime}=-s;\) decir,
\[(\sin x)^{\prime}=\cos x \text { and }(\cos x)^{\prime}=-\sin x.\]
- Prueba
-
Baste considerar los intervalos\(\overline{J_{0}}\) y\(\overline{J_{1}},\) para por (15), todas las propiedades de\(s\) y\(c\) repetirse, con punto\(2 \pi,\) sobre el resto de\(E^{1}\).
Por (13),
\[s=F_{0}^{-1} \text { on } \overline{J_{0}}=\left[-\frac{\pi}{2}, \frac{\pi}{2}\right],\]
donde\(F_{0}\) es diferenciable en\(I=(-1,1).\) Así Teorema 3 de §2 muestra que\(s\) es diferenciable en\(J_{0}=(-\pi / 2, \pi / 2)\) y que
\[s^{\prime}(q)=\frac{1}{F_{0}^{\prime}(p)} \text { whenever } p \in I \text { and } q=F_{0}(p);\]
es decir,\(q \in J\) y\(p=s(q).\) Sin embargo, por el Teorema 3 (iii),
\[F_{0}^{\prime}(p)=\frac{1}{\sqrt{1-p^{2}}}.\]
Por lo tanto,
\[s^{\prime}(q)=\sqrt{1-\sin ^{2} q}=\cos q=c(q), \quad q \in J.\]
Esto prueba el teorema para los puntos interiores de\(\overline{J_{0}}\) lo que\(s\) se refiere.
Como
\[c=\sqrt{1-s^{2}}=\left(1-s^{2}\right)^{\frac{1}{2}} \text{ on } J_{0} \text{ (by (13)),}\]
podemos usar la regla de la cadena (Teorema 3 en §1) para obtener
\[c^{\prime}=\frac{1}{2}\left(1-s^{2}\right)^{-\frac{1}{2}}(-2 s) s^{\prime}=-s\]
al señalar que\(s^{\prime}=c=\left(1-s^{2}\right)^{\frac{1}{2}}\) en\(J_{0}.\) De igual manera, utilizando (14), se prueba que\(s^{\prime}=c\) y\(c^{\prime}=-s\) en\(J_{1}\) (interior de\(\overline{J_{1}})\).
A continuación, deje\(q\) ser un punto final, digamos,\(q=\pi / 2.\) tomamos la derivada izquierda
\[s_{-}^{\prime}(q)=\lim _{x \rightarrow q^{-}} \frac{s(x)-s(q)}{x-q}, \quad x \in J_{0}.\]
Por regla de L'Hôpital, obtenemos
\[s_{-}^{\prime}(q)=\lim _{x \rightarrow q^{-}} \frac{s^{\prime}(x)}{1}=\lim _{x \rightarrow q^{-}} c(x)\]
ya que\(s^{\prime}=c\) en\(J_{0}.\) Sin embargo,\(s=F_{0}^{-1}\) se deja continuo en\(q\) (¿por qué?) ; de ahí que así sea\(c=\sqrt{1-s^{2}}.\) (¿Por qué?) Por lo tanto,
\[s_{-}^{\prime}(q)=\lim _{x \rightarrow q^{-}} c(x)=c(q), \quad \text {as required.}\]
De igual manera, se demuestra que\(s_{+}^{\prime}(q)=c(q).\) De ahí\(s^{\prime}(q)=c(q)\) y\(c^{\prime}(q)=-s(q)\) como antes. \(\quad \square\)
Las otras funciones trigonométricas se reducen a\(s\) y\(c\) por sus fórmulas definitorias
\[\tan x=\frac{\sin x}{\cos x}, \cot x=\frac{\cos x}{\sin x}, \sec x=\frac{1}{\cos x}, \text { and } \csc x=\frac{1}{\sin x},\]
por lo que no nos detendremos en ellos a detalle. Las diversas leyes trigonométricas siguen fácilmente de nuestras definiciones actuales; para pistas, ver los problemas a continuación.


