1.6: Fórmula de Euler
- Page ID
- 109919
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La fórmula de Euler (pronunciada 'aceiteras') conecta exponenciales complejos, coordenadas polares y senos y cosenos. Convierte identidades trig desordenadas en reglas ordenadas para exponenciales. Lo usaremos mucho. La fórmula es la siguiente:
\[e^{i\theta} = \cos (\theta) + i \sin (\theta). \label{1.6.1}\]
Hay muchas formas de acercarse a la fórmula de Euler. Nuestro enfoque es simplemente tomar la Ecuación\ ref {1.6.1} como la definición de exponenciales complejos. Esto es legal, pero no demuestra que sea una buena definición. Para ello necesitamos mostrar que el\(e^{i \theta}\) obedece todas las reglas que esperamos de un exponencial. Para ello pasamos sistemáticamente por las propiedades de los exponenciales y comprobamos que mantienen para exponenciales complejos.
\(e^{i \theta}\)se comporta como un verdadero exponencial
\(e^{i t}\)diferencia como se esperaba:
\[\dfrac{de^{it}}{dt} = ie^{it}.\nonumber\]
- Prueba
-
Esto se desprende directamente de la definición de la Ecuación\ ref {1.6.1}:
\[ \begin{align*} \dfrac{de^{it}}{dt} &= \dfrac{d}{dt} (\cos (t) + i \sin (t)) \\[4pt] &= -\sin (t) + i \cos (t) \\[4pt] &= i (\cos (t) + i \sin (t)) \\[4pt] &= ie^{it}. \end{align*}\]
\[e^{i \cdot 0} = 1 . \nonumber\]
- Prueba
-
Esto se desprende directamente de la definición de la Ecuación\ ref {1.6.1}:
\(e^{i \cdot 0} = \cos (0) + i \sin (0) = 1\).
Las reglas habituales de los exponentes sostienen:
\[e^{ia} e^{ib} = e^{i(a + b)}.\nonumber\]
- Prueba
-
Esto se basa en las fórmulas de adición de coseno y seno y la definición en la ecuación\ ref {1.6.1}:
\[\begin{align*} e^{ia} \cdot e^{ib} & = (\cos (a) + i \sin (a)) \cdot (\cos (b) + i \sin (b)) \\[4pt] & = \cos (a) \cos (b) - \sin (a) \sin (b) + i (\cos (a) \sin (b) + \sin (a) \cos (b)) \\[4pt] & = \cos (a + b) + i \sin (a + b) = e^{i (a + b)}. \end{align*}\]
La definición de\(e^{i \theta}\) es consistente con la serie de potencia para\(e^x\).
- Prueba
-
Para ver esto tenemos que recordar la serie power para\(e^x\),\(\cos (x)\) y\(\sin (x)\). Ellos son
\[\begin{align*} e^x & = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dfrac{x^4}{4!} + ... \\[4pt] \cos (x) & = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \ldots \\[4pt] \sin (x) & = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} + ... \end{align*}\]
Ahora podemos escribir la serie power para\(e^{i \theta}\) y luego dividirla en la serie power para seno y coseno:
\[\begin{align*} e^{i \theta} & = \sum_{0}^{\infty} \dfrac{(i\theta)^n}{n!} \\[4pt] & = \sum_{0}^{\infty} (-1)^k \dfrac{\theta ^{2k}}{(2k)!} + i \sum_{0}^{\infty} (-1)^k \dfrac{\theta ^{2k + 1}}{(2k + 1)!} \\[4pt] & = \cos (\theta) + i \sin (\theta). \end{align*}\]
Por lo que la definición de la fórmula de Euler es consistente con la serie de potencia habitual para\(e^x\).
Propiedades P1-P4 debería convencerte de que\(e^{i \theta}\) se comporta como un exponencial.
Exponenciales Complejos y Forma Polar
Ahora pasemos a la relación entre coordenadas polares y exponenciales complejos.
Supongamos que\(z = x + iy\) tiene coordenadas polares\(r\) y\(\theta\). Es decir, tenemos\(x = r \cos (\theta)\) y\(y = r \sin (\theta)\). Así, obtenemos la relación importante
\[ \begin{align*} z &= x + iy \\[4pt] &= r \cos (\theta) + i r \sin (\theta) \\[4pt] &= r (\cos (\theta) + i \sin (\theta)) \\[4pt] &= r e^{i \theta}. \end{align*}\]
Esto es tan importante que no debes proceder sin entender. También lo registramos sin la ecuación intermedia.
\[z = x + iy = r e^{i \theta}.\]
Porque\(r\) y\(\theta\) son las coordenadas polares de la\((x, y)\) que llamamos\(z = r e^{i \theta}\) la forma polar de\(z\).
Verifiquemos ahora que la magnitud, el argumento, la conjugación, la multiplicación y la división son fáciles en forma polar.
\(|e^{i \theta}| = 1\).
- Prueba
-
\[ \begin{align*} |e^{i \theta}| &= |\cos (\theta) + i \sin (\theta)| \\[4pt] &= \sqrt{\cos ^2 (\theta) + \sin ^2 (\theta)} \\[4pt] &= 1 . \end{align*}\]
En palabras, esto dice que siempre\(e^{i \theta}\) está en el círculo unitario - ¡esto es útil para recordar!
Del mismo modo, si\(z = r e^{i \theta}\) entonces\(|z| = r\). Esto se puede calcular, pero debe quedar claro a partir de las definiciones:\(|z|\) es la distancia desde\(z\) el origen, que es exactamente la misma definición que para\(r\).
Si\(z = r e^{i \theta}\) entonces\(\text{arg} (z) = \theta\).
- Prueba
-
Esta es nuevamente la definición: el argumento es el ángulo polar\(\theta\).
\(\overline{(z = r e^{i \theta})} = r e^{-i \theta}\).
- Prueba
-
\[ \begin{align*} \overline{(z = r e^{i \theta})} &= \overline{r (\cos (\theta) + i \sin (\theta))} \\[4pt] &= r (\cos (\theta) - i \sin (\theta)) \\[4pt] &= r(\cos (-\theta) + i \sin (-\theta)) \\[4pt] &= r e^{-i \theta}. \end{align*}\]
En palabras: la conjugación compleja cambia el signo del argumento.
Si\(z_1 = r_1 e^{i \theta_1}\) y\(z_2 = r_2 e^{i \theta_2}\) entonces
\[z_1 z_2 = r_1 r_2 e^{i (\theta_1 + \theta_2)}. \nonumber\]
Esto es lo que los matemáticos llaman trivial para ver, solo anotar la multiplicación. En palabras, la fórmula dice que para\(z_1 z_2\) las magnitudes se multiplican y los argumentos suman.
De nuevo es trivial que
\(\dfrac{r_1 e^{i \theta_1}}{r_2 e^{i \theta_2}} = \dfrac{r_1}{r_2} e^{i (\theta_1 - \theta_2)}.\)
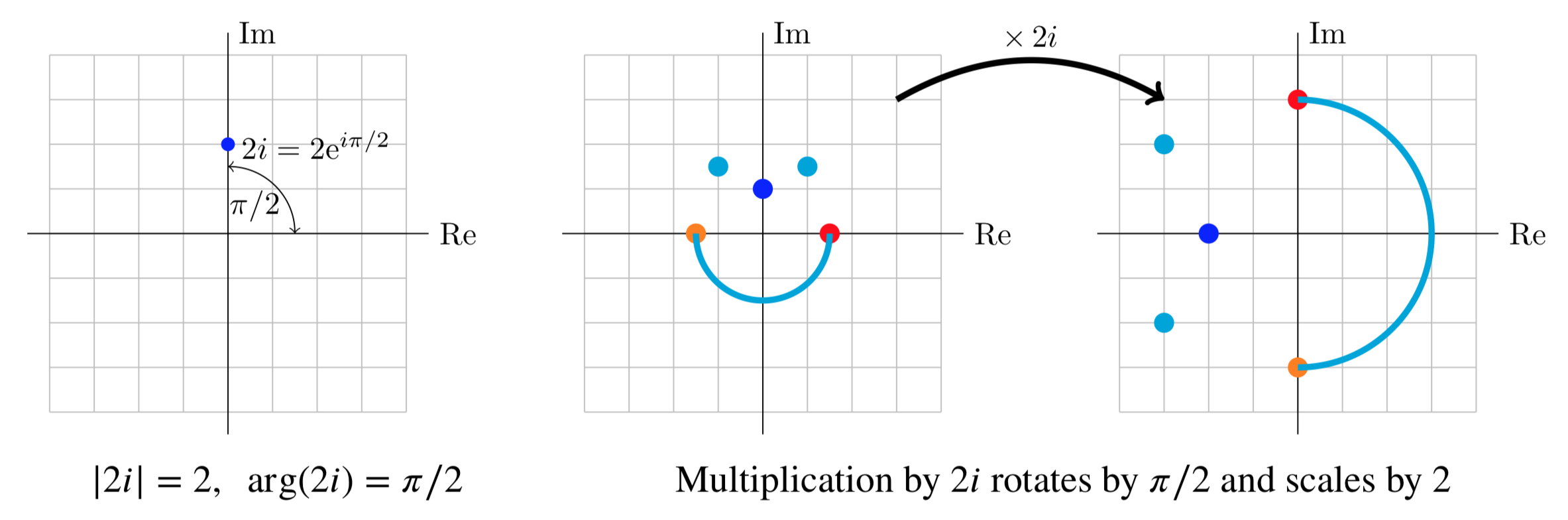
He aquí un ejemplo sencillo pero importante. Al mirar la gráfica vemos que el número\(2i\) tiene magnitud 2 y argumento\(\pi/2\). Entonces en coordenadas polares es igual\(2e^{i \pi /2}\). Esto significa que la multiplicación por\(2i\) multiplica las longitudes por 2 y se suma\(\pi/2\) a los argumentos, es decir, gira por\(90^{\circ}\). El efecto se muestra en las figuras a continuación
Vamos a calcular\((1 + i)^6\) y\((\dfrac{1 + i \sqrt{3}}{2})^3\)
Solución
\(1 + i\)tiene magnitud =\(\sqrt{2}\) y\(\text{arg} = \pi /4\), entonces\(1 + i = \sqrt{2} e^{i \pi /4}\). Rasing a un poder ahora es fácil:
\((1 + i)^6 = (\sqrt{2} e^{i \pi /4})^6 = 8 e^{6i \pi /4} = 8 e^{3i \pi /2} = -8i\).
Del mismo modo\(\dfrac{1 + i\sqrt{3}}{2} = e^{i \pi / 3}\),, entonces\((\dfrac{1 + i\sqrt{3}}{2})^3 = (1 \cdot e^{i \pi / 3})^3 = e^{i \pi} = -1\)
Complexificación o reemplazo complejo
En el siguiente ejemplo ilustraremos la técnica de complexificación o reemplazo complejo. Esto se puede utilizar para simplificar una integral trigonométrica. Será útil cuando necesitemos calcular ciertas integrales.
Usar reemplazo complejo para calcular
\[I = \int e^x \cos (2x)\ dx.\]
Solución
Tenemos la fórmula de Euler
\[e^{2ix} = \cos (2x) + i \sin (2x),\]
así\(\cos (2x) = \text{Re} (e^{2ix})\). El truco de reemplazo complejo es reemplazar\(\cos (2x)\) por\(e^{2ix}\). Obtenemos (justificación abajo)
\[I_c = \int e^x \cos 2x + ie^x \sin 2x \ dx\]
con
\[I = \text{Re} (I_c)\]
La computación\(I_c\) es sencilla:
\[I_c = \int e^x e^{i2x}\ dx = \int e^{x(1 + 2i)}\ dx = \dfrac{e^{x(1 + 2i)}}{1 + 2i}.\]
Aquí haremos el cálculo primero en coordenadas rectangulares. En aplicaciones, por ejemplo a lo largo del 18.03, a menudo se prefiere la forma polar porque es más fácil y da la respuesta en una forma más útil.
\[\begin{array} {rcl} {I_c} & = & {\dfrac{e^{x(1 + 2i)}}{1 + 2i} \cdot \dfrac{1 - 2i}{1 - 2i}} \\ {} & = & {\dfrac{e^x (\cos (2x) + i \sin (2x)) (1 - 2i)}{5}} \\ {} & = & {\dfrac{1}{5} e^x (\cos (2x) + 2 \sin (2x) + i (-2 \cos (2x) + \sin (2x)))} \end{array}\]
Entonces,
\[I = \text{Re} (I_c) = \dfrac{1}{5} e^x (\cos (2x) + 2\sin (2x)).\]
Justificación de reemplazo complejo. El truco viene al agregar inteligentemente una nueva integral a la\(I\) siguiente manera, Let\(J = \int e^x \sin (2x)\ dx\). Entonces dejamos
\[I_c = I + iJ = \int e^x (\cos (2x) + i \sin (2x)) \ dx = \int e^x 2^{2ix}\ dx.\]
Claramente, por construcción,\(\text{Re} (I_c) = I\) como se ha afirmado anteriormente.
Alternativa usando coordenadas polares para simplificar la expresión para\(I_c\):
En forma polar, tenemos\(1 + 2i = re^{i \phi}\), dónde\(r = \sqrt{5}\) y\(\phi = \text{arg} (1 + 2i) = \text{tan}^{-1} (2)\) en el primer cuadrante. Entonces:
\(I_c = \dfrac{e^{x(1 + 2i)}}{\sqrt{5} e^{i \phi}} = \dfrac{e^x}{\sqrt{5}} e^{i(2x - \phi)} = \dfrac{e^x}{\sqrt{5}} (\cos (2x - \phi) + i \sin (2x - \phi))\).
Por lo tanto,
\[I = \text{Re} (I_c) = \dfrac{e^x}{\sqrt{5}} \cos (2x - \phi).\]
\(N\)th raíces
Vamos a necesitar poder encontrar las raíces\(n\) th de números complejos, es decir, resolver ecuaciones de la forma
\[z^N = c,\]
donde\(c\) es un número complejo dado. Esto se puede hacer de la manera más conveniente expresando\(c\) y\(z\) en forma polar,\(c = Re^{i \phi}\) y\(z = re^{i \theta}\). Entonces, al sustituir, tenemos que resolver
\[r^N e^{iN \theta} = Re^{i \phi}\]
Para que los números complejos de la izquierda y la derecha sean iguales, sus magnitudes deben ser las mismas y sus argumentos solo pueden diferir en un múltiplo entero de\(2\pi\). Esto da
\[r = R^{1/N} \; (N \theta = \phi + 2\pi n), \; where\;n = 0, \pm 1, \pm 2, ...\]
Resolviendo para\(\theta\), tenemos
\[\theta = \dfrac{\phi}{N} + \dfrac{2\pi n}{N}.\]
Encuentra todas las 5 quintas raíces de 2.
Solución
Porque\(c = 2\), tenemos\(R = 2\) y\(\phi = 0\), así las quintas raíces de 2 son
\(z_n = 2^{1/5} e^{2n \pi i/5}\), donde\(n = 0, \pm 1, \pm 2, ...\)
Mirando el lado derecho vemos que para\(n = 5\) tenemos\(2^{1/5} e^{2\pi i}\) que es exactamente lo mismo que la raíz cuando\(n = 0\), es decir\(2^{1/5} e^{0i}\). Del mismo modo\(n = 6\) da exactamente la misma raíz que\(n = 1\), y así sucesivamente. Esto quiere decir, tenemos 5 raíces diferentes correspondientes a\(n = 0, 1, 2, 3, 4\).
\(z_n = 2^{1/5}, e^{1/5} e^{2\pi i/5}, e^{1/5} e^{4\pi i/5}, e^{1/5} e^{6\pi i/5}, e^{1/5} e^{8\pi i/5}\)
Del mismo modo podemos decir que en general\(c = Re^{i \phi}\) tiene\(N\) distintas raíces\(N\) th:
\(z_n = r^{1/N} e^{i \phi / N + i 2\pi (n/N)}\)para\(n = 0, 1, 2, ..., N - 1\).
Encuentra las 4 cuartas raíces de 1.
Solución
Tenemos que resolver\(z^4 = 1\), entonces\(\phi = 0\). Entonces las 4 cuartas raíces distintas están en forma polar
\[z_n = 1, e^{i \pi /2}, e^{i \pi}, e^{i 3 \pi /2}\]
y en la representación cartesiana
\[z_n = 1, i, -1, -i.\]
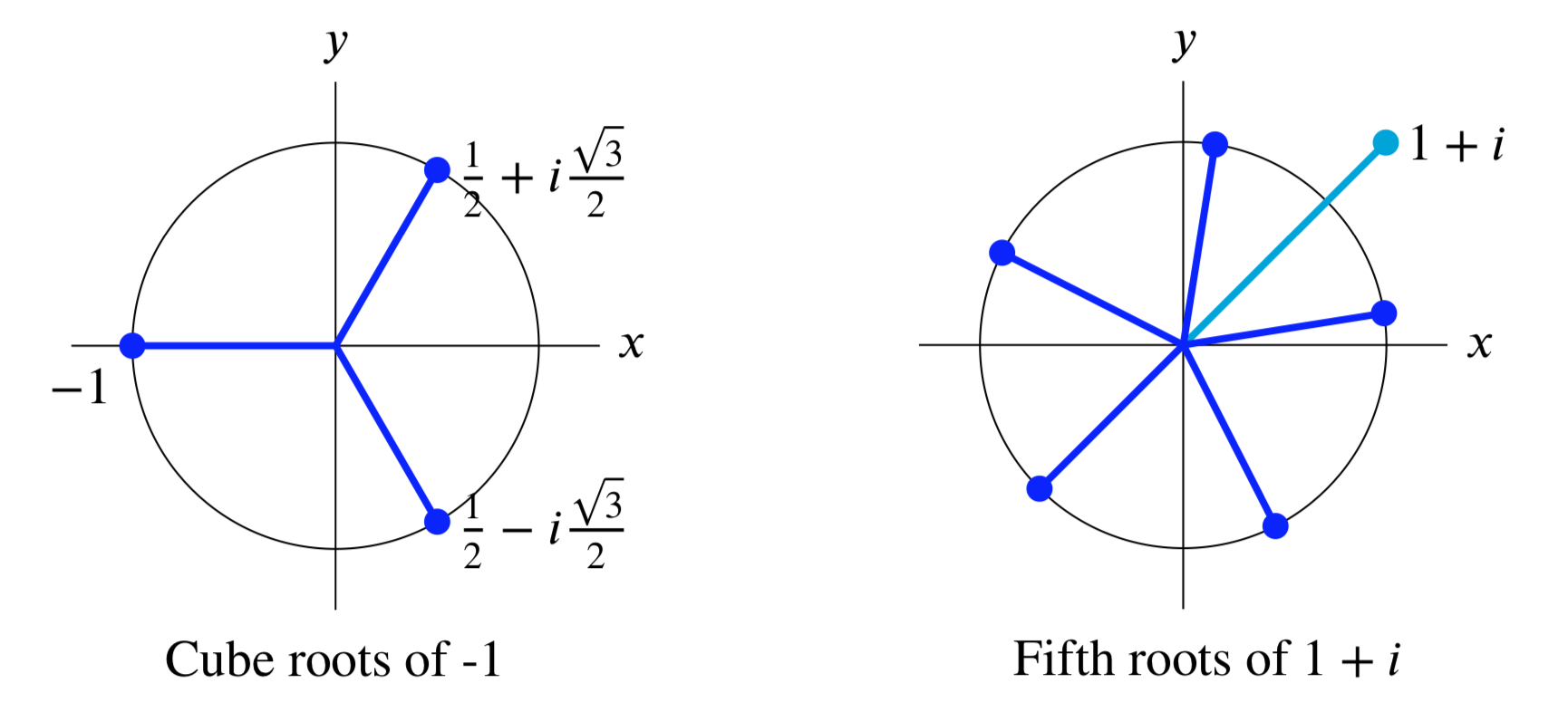
Encuentra las 3 raíces cubicas de -1.
Solución
\(z^2 = -1 = e^{i \pi + i 2 \pi n}\). Entonces,\(z_n = e^{i \pi + i 2 \pi (n/3)}\) y las 3 raíces cubitas son\(e^{i \pi /3}\),\(e^{i \pi}\),\(e^{i 5 \pi /3}\). Como\(\pi /3\) radianes es\(60^{\circ}\) podemos simplificar:
\(e^{i \pi /3} = \cos (\pi / 3) + i \sin (\pi /3) = \dfrac{1}{2} + i \dfrac{\sqrt{3}}{2} \Rightarrow z_n = -1, \dfrac{1}{2} \pm i \dfrac{\sqrt{3}}{2}\)
Encuentra las 5 quintas raíces de\(1 + i\).
Solución
\[z^5 = 1 + i = \sqrt{2} e^{i (\pi / 4 + 2n\pi)}\]
para\(n = 0, 1, 2, ...\). Entonces, las 5 quintas raíces son
\(2^{1/10} e^{i\pi /20}\),\(2^{1/10} e^{i9\pi /20}\),\(2^{1/10} e^{i17\pi /20}\),\(2^{1/10} e^{i25\pi /20}\),\(2^{1/10} e^{i33\pi /20}\).
Usando una calculadora podríamos escribir estos numéricamente como\(a + bi\), pero no hay una simplificación fácil.
Deberíamos comprobar que nuestra técnica funciona como se esperaba para un problema sencillo. Encuentra las 2 raíces cuadradas de 4.
Solución
\(z^2 = 4 e^{i2 \pi n}\). Entonces,\(z_n = 2e^{i \pi n}\), con\(n = 0, 1\). Entonces las dos raíces son\(2e^0 = 2\) y\(2e^{i\pi} = -2\) como se esperaba!
geometría de\(N\) las raíces
Al observar los ejemplos anteriores vemos que las raíces siempre están espaciadas uniformemente alrededor de un círculo centrado en el origen. Por ejemplo, las quintas raíces de\(1 + i\) están espaciadas en incrementos de\(2\pi / 5\) radianes alrededor del círculo de radio\(2^{1/5}\).
Tenga en cuenta también que las raíces de los números reales siempre vienen en pares conjugados.
