1.7: La función exponencial
- Page ID
- 109892
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Tenemos la fórmula de Euler:\(e^{i\theta} = \cos (\theta) + i \sin (\theta)\). Podemos extender esto a la compleja función exponencial\(e^z\).
Para\(z = x + iy\) la función exponencial compleja se define como
\[e^z = e^{x + iy} = e^x e^{iy} = e^x (\cos (y) + i \sin (y)).\]
En esta definición\(e^x\) se encuentra la función exponencial habitual para una variable real\(x\).
Es fácil ver que todas las reglas habituales de los exponentes sostienen:
- \(e^0 = 1\)
- \(e^{z_1 + z_2} = e^{z_1} e^{z_2}\)
- \((e^z)^n = e^{nz}\)para enteros positivos\(n\).
- \((e^z)^{-1} = e^{-z}\)
- \(e^z \ne 0\)
Resulta que la propiedad\(\dfrac{de^z}{dz} = e^z\) también tiene, pero aún no podemos probarlo porque no hemos definido a qué nos referimos con el derivado complejo\(\dfrac{d}{dz}\).
Aquí hay algunas propiedades más simples, pero extremadamente importantes de\(e^z\). Debes llegar a ser fluido en su uso y saber cómo probarlos. - \(|e^{i \theta}| = 1\)
Comprobante.
\(|e^{i \theta}| = |\cos (\theta) + i \sin (\theta)| = \sqrt{\cos ^2 (\theta) + \sin ^2 (\theta)} = 1\) - \(|e^{x + iy}| = e^x\)(como de costumbre\(z = x + iy\) y\(x, y\) son reales).
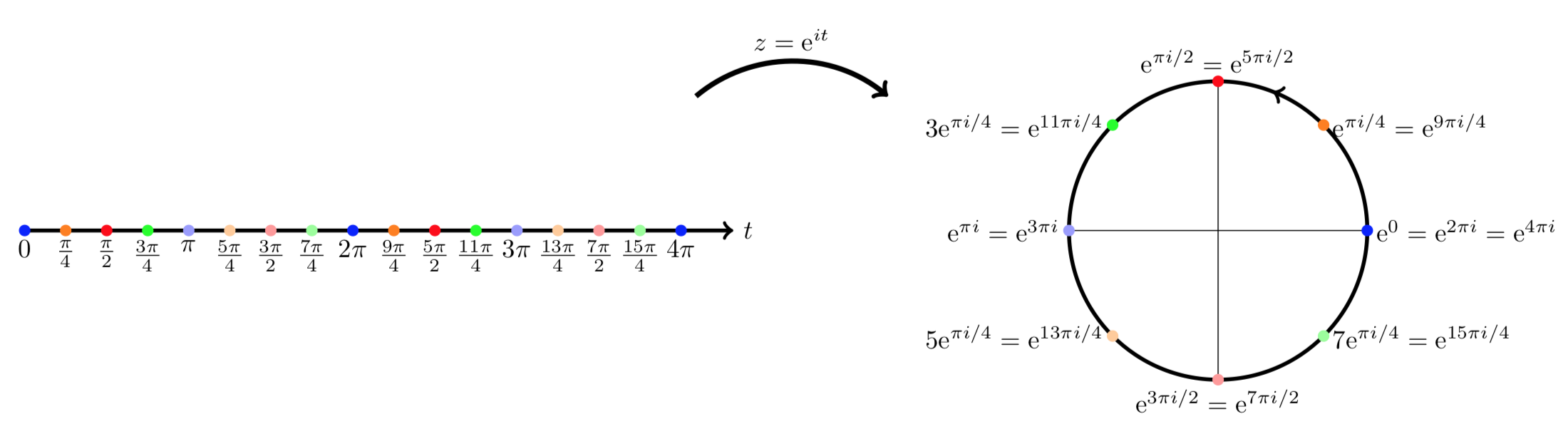
Comprobante. Deberías ser capaz de suplir esto. Si no: pregúntale a un profesor o TA. - El camino\(e^{it}\) para se\(0 < t < \infty\) envuelve en sentido antihorario alrededor del círculo unitario. Lo hace infinitamente muchas veces. Esto se ilustra en la siguiente imagen.