Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

1.8: Funciones complejas como asignaciones

Última actualización

30 oct 2022
Guardar como PDF
- 1.7: La función exponencial
- 1.9: La función arg (z)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Una función compleja $w = f(z)$ es difícil de graficar porque toma 4 dimensiones: 2 para $z$ y 2 para $w$ . Entonces, para visualizarlos pensaremos en funciones complejas como mapeos. Es decir, pensaremos en tomar un punto en el $z$ plano complejo y mapearlo (enviarlo) a un punto en el $w$ plano complejo. $w = f(z)$

Utilizaremos los siguientes términos y símbolos para discutir las asignaciones.

Una función también se $w = f(z)$ llamará mapeo de $z$ a $w$ .
Alternativamente escribiremos $z \mapsto w$ o $z \mapsto f(z)$ . Esto se lee como " $z$ mapas a $w$ ”.
Diremos que " $w$ es la imagen de $z$ debajo del mapeo” o más simplemente " $w$ es la imagen de $z$ ”.
Si tenemos un conjunto de puntos en el $z$ -plano hablaremos de la imagen de ese conjunto bajo el mapeo.
Por ejemplo, bajo el mapeo $z \mapsto iz$ la imagen del $z$ eje imaginario es el $w$ eje real.

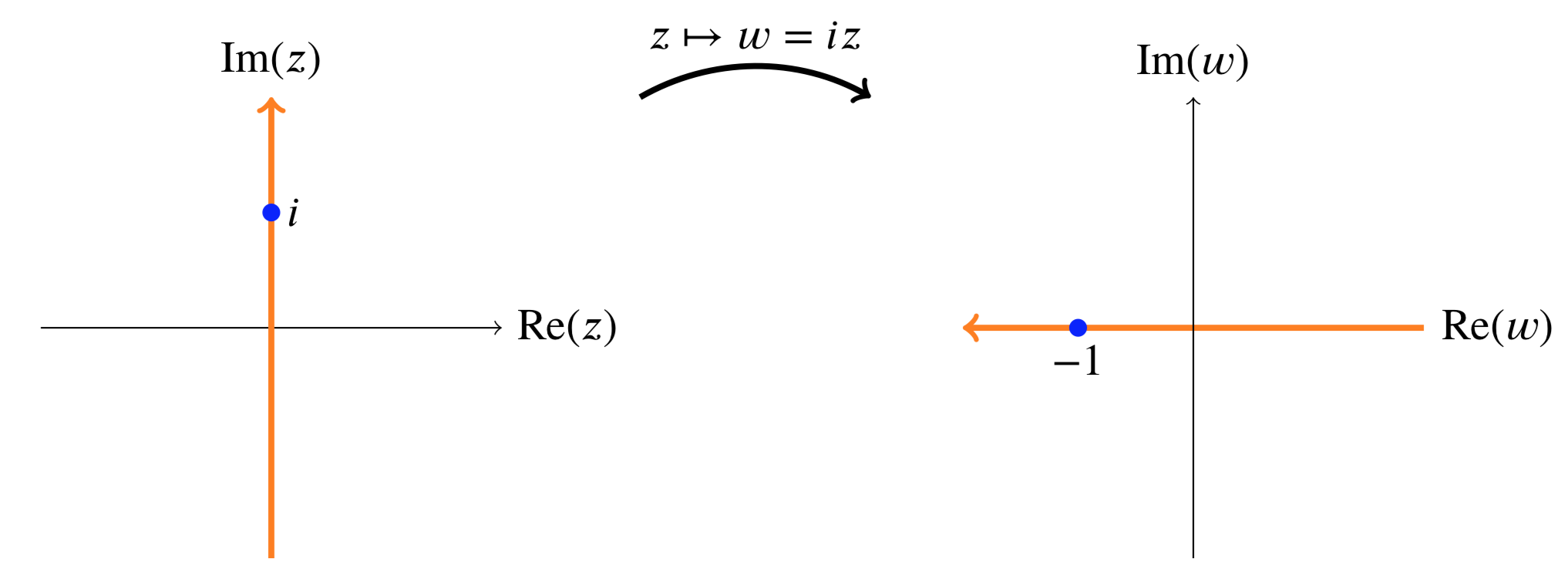
$2020-08-14 8.29.54.png$
La imagen del eje imaginario bajo $z \mapsto iz$

Ejemplo $\PageIndex{1}$

El mapeo $w = z^2$ . Visualizamos esto poniendo el $z$ -plano a la izquierda y el $w$ -plano a la derecha. Luego dibujamos diversas curvas y regiones en el $z$ plano -y la imagen correspondiente debajo $z^2$ en el $w$ plano -plano.

En la primera figura mostramos que los rayos del origen son mapeados por $z^2$ a los rayos del origen. Vemos que

El rayo $L_2$ en $\pi /4$ radianes se mapea al rayo $f(L_2)$ en $\pi /2$ radianes.
Los rayos $L_2$ y ambos $L_6$ están mapeados al mismo rayo. Esto es cierto para cada par de rayos diametralmente opuestos.
Un rayo en ángulo $\theta$ se mapea al rayo en ángulo $2 \theta$ .

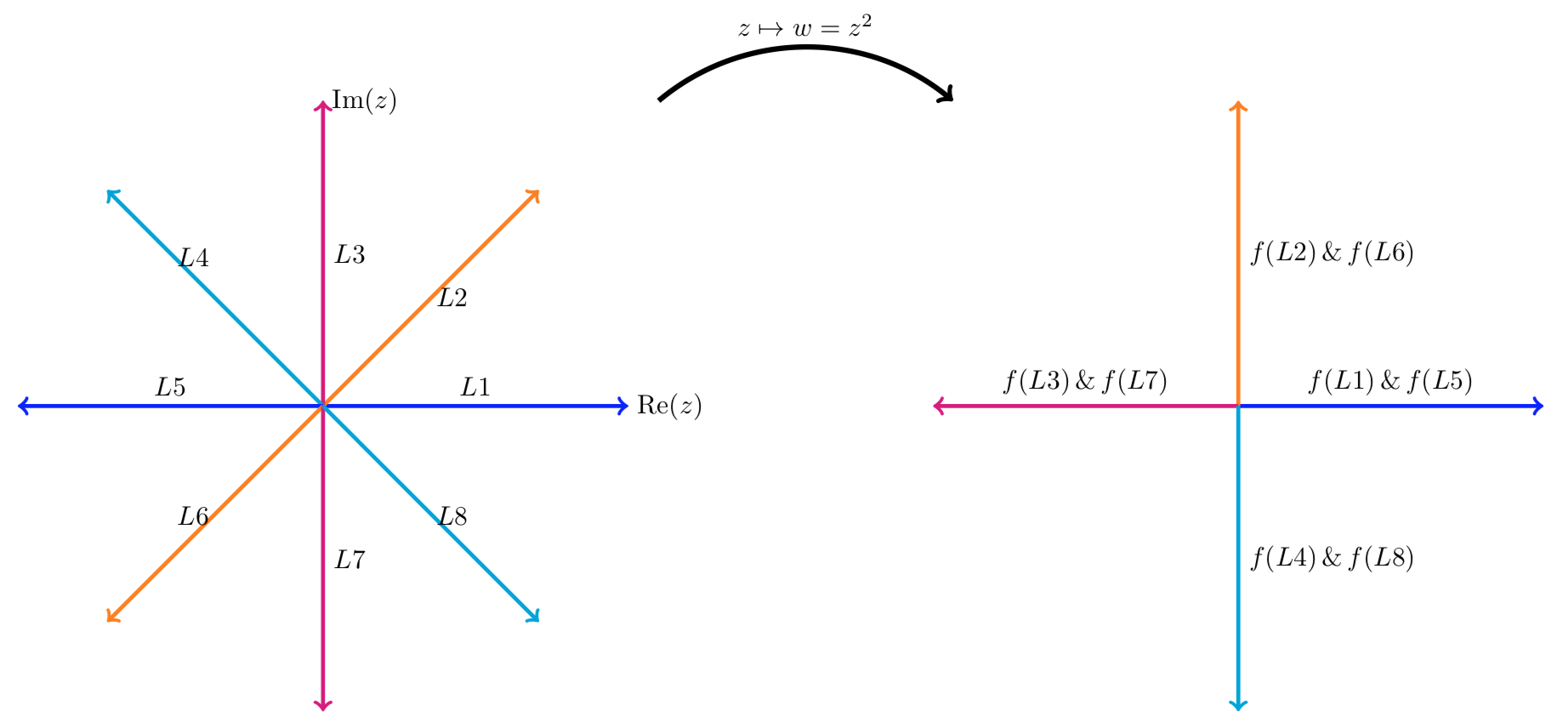
$2020-08-14 8.34.34.png$
$f(z) = z^2$ mapea los rayos desde el origen a los rayos del origen.

La siguiente figura da otra vista del mapeo. Aquí vemos franjas verticales en el primer cuadrante que se mapean a franjas parabólicas que viven en el primer y segundo cuadrantes.

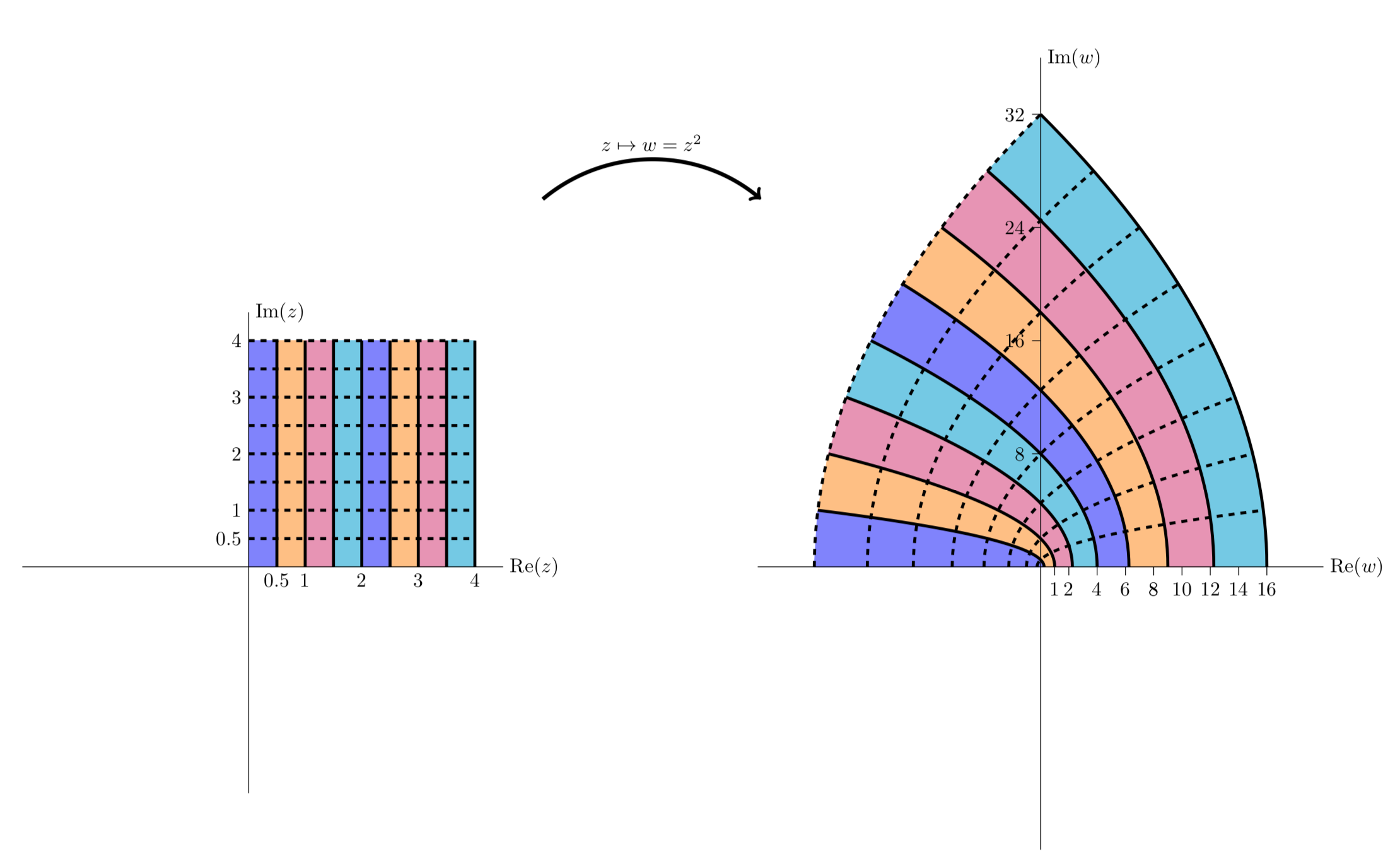
$2020-08-14 8.37.49.png$
$z^2 = (x^2 - y^2) + i2xy$ mapea líneas verticales a parábolas orientadas a la izquierda.

La siguiente cifra es similar a la anterior, salvo que en esta figura observamos franjas verticales tanto en el primer como en el segundo cuadrantes. Vemos que mapean a franjas parabólicas que viven en los cuatro cuadrantes.

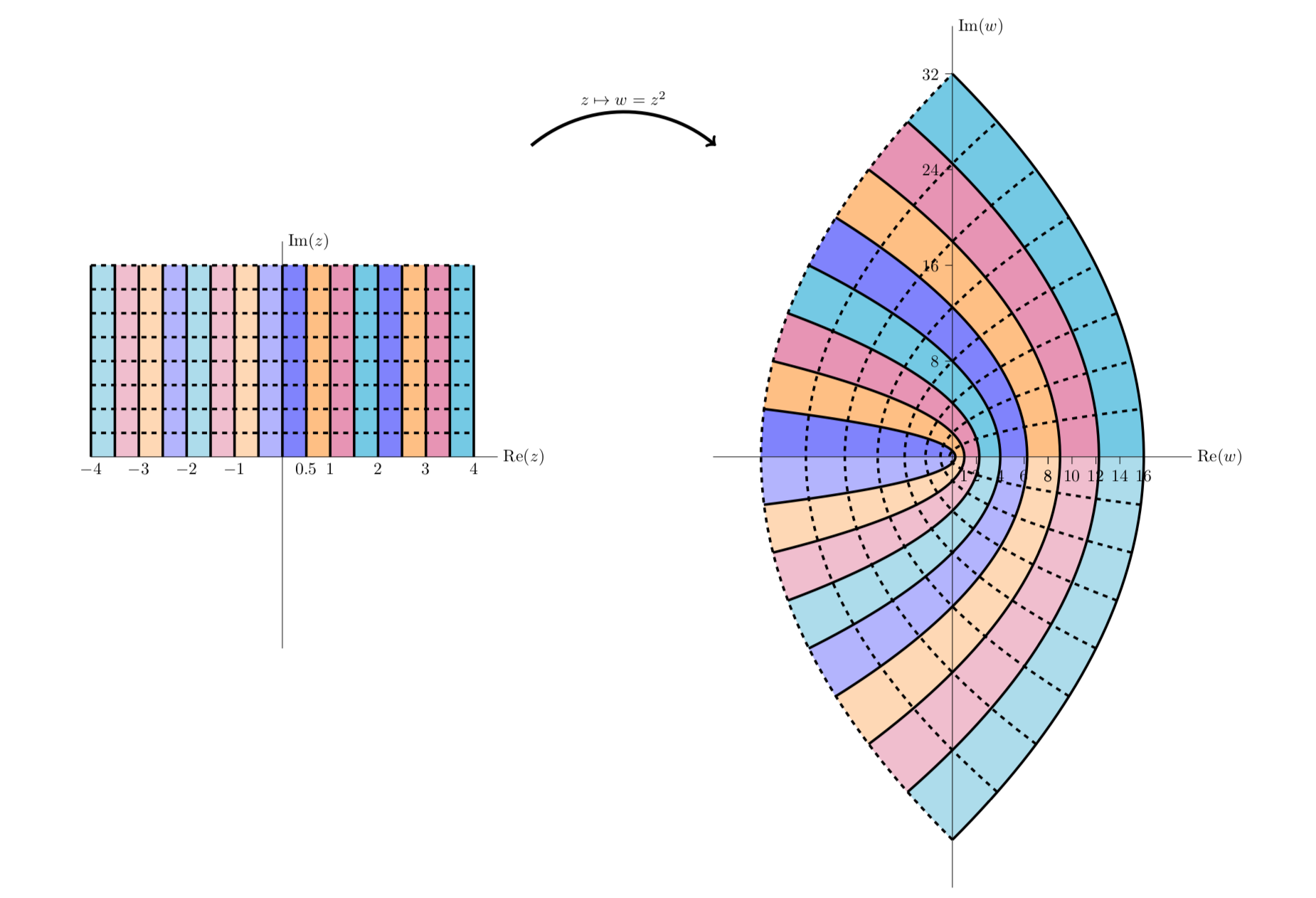
$2020-08-14 8.42.09.png$
$f(z) = z^2$ mapea los dos primeros cuadrantes a todo el plano.

En la siguiente figura se muestra el mapeo de franjas en el primer y cuarto cuadrantes. El mapa de la imagen es idéntico a la figura anterior. Esto se debe a que el cuarto cuadrante es menos el segundo cuadrante, pero $z^2 = (-z)^2$

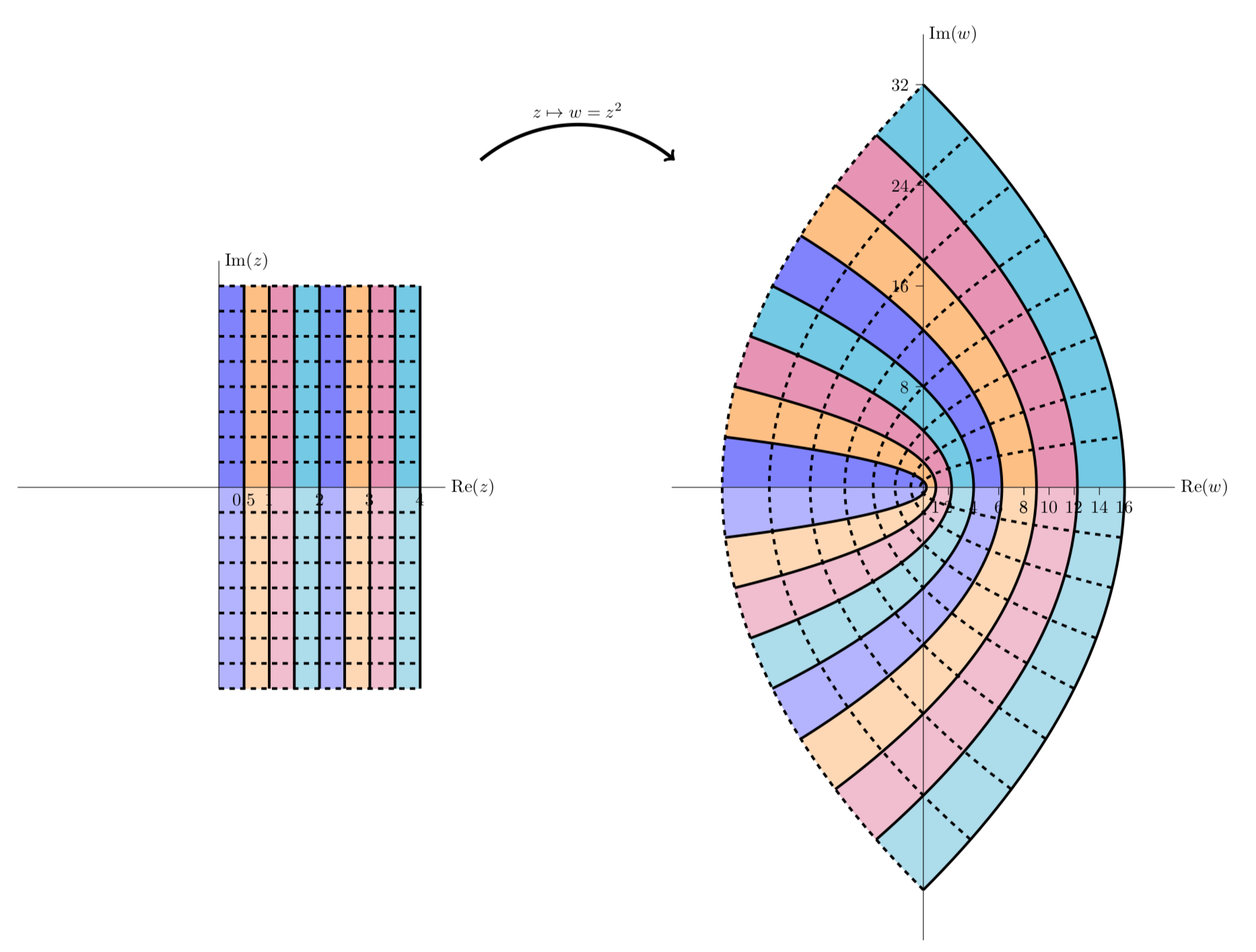
$2020-08-14 8.44.31.png$

Las franjas verticales en el cuadrante 4 se mapean de manera idéntica a las franjas verticales en el cuadrante 2.

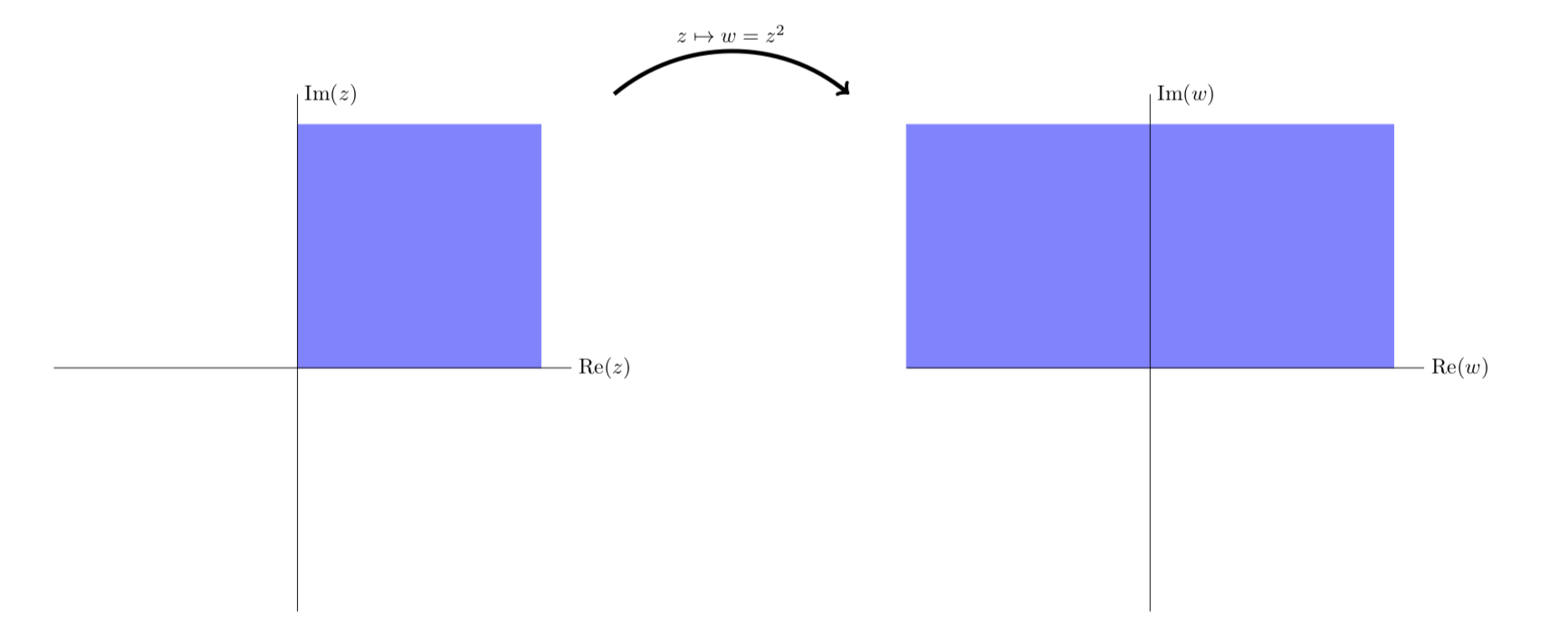
$2020-08-14 8.46.02.png$

Vista simplificada del primer cuadrante mapeado a los dos primeros cuadrantes.

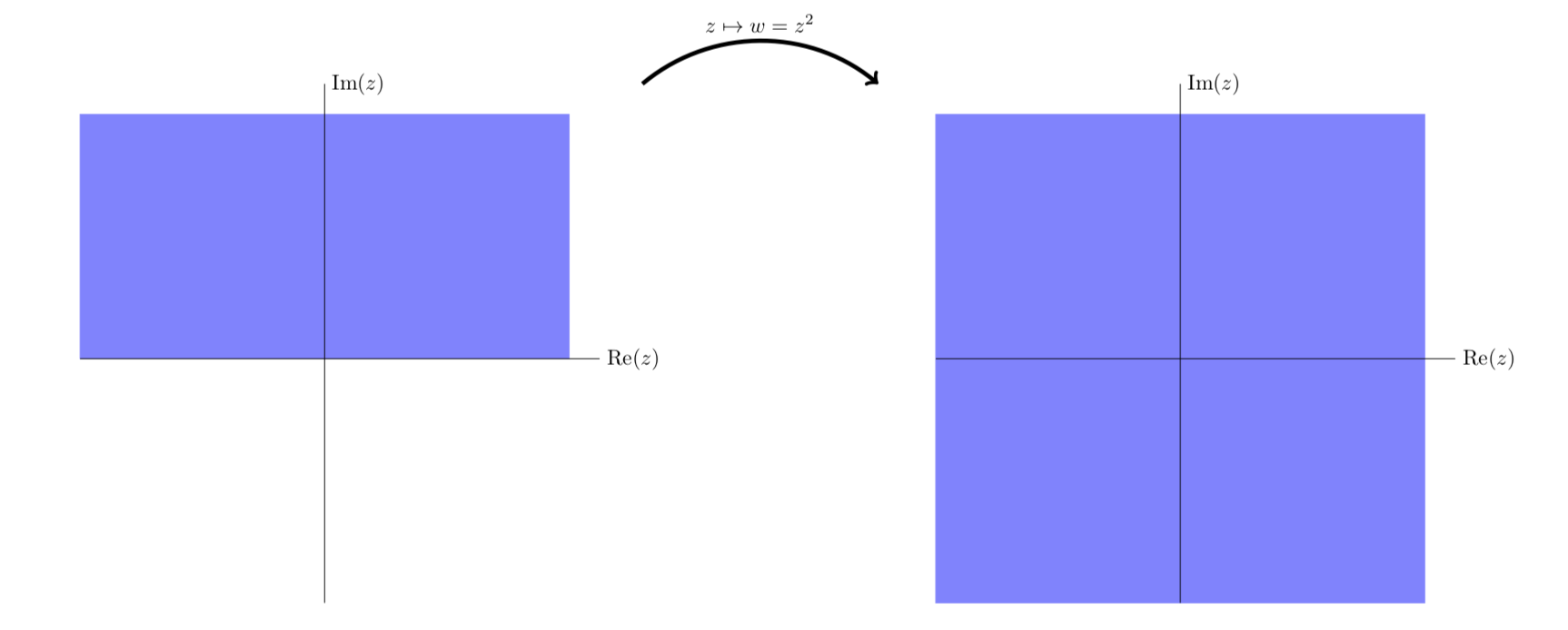
$2020-08-14 8.46.45.png$

Vista simplificada de los dos primeros cuadrantes mapeados a todo el plano.

Ejemplo $\PageIndex{2}$

El mapeo $w = e^z$ . Aquí presentamos una serie de gráficas que muestran cómo se mapea la función exponencial $z$ a $w$ .

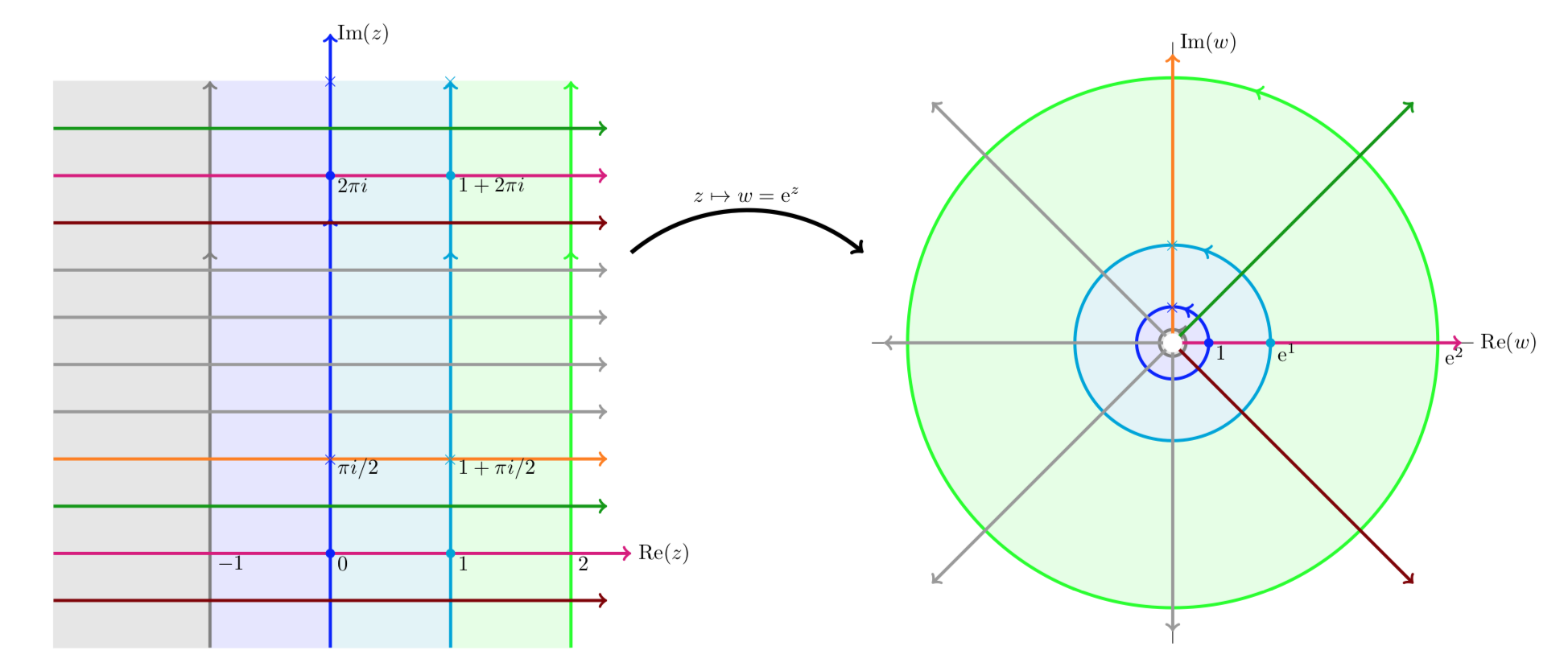
$2020-08-14 8.51.30.png$

Observe que las líneas verticales se mapean a círculos y las líneas horizontales a los rayos desde el origen.

Las siguientes cuatro figuras muestran esencialmente lo mismo: la función exponencial mapea franjas horizontales a sectores circulares. Cualquier franja horizontal de ancho $2\pi$ se mapea a todo el plano menos el origen,

Debido a que el plano menos el origen aparece frecuentemente le damos un nombre:

Definición: plano perforado

El plano perforado es el plano complejo menos el origen. En símbolos podemos escribirlo como $C$ - {0} o $C$ /{0}.

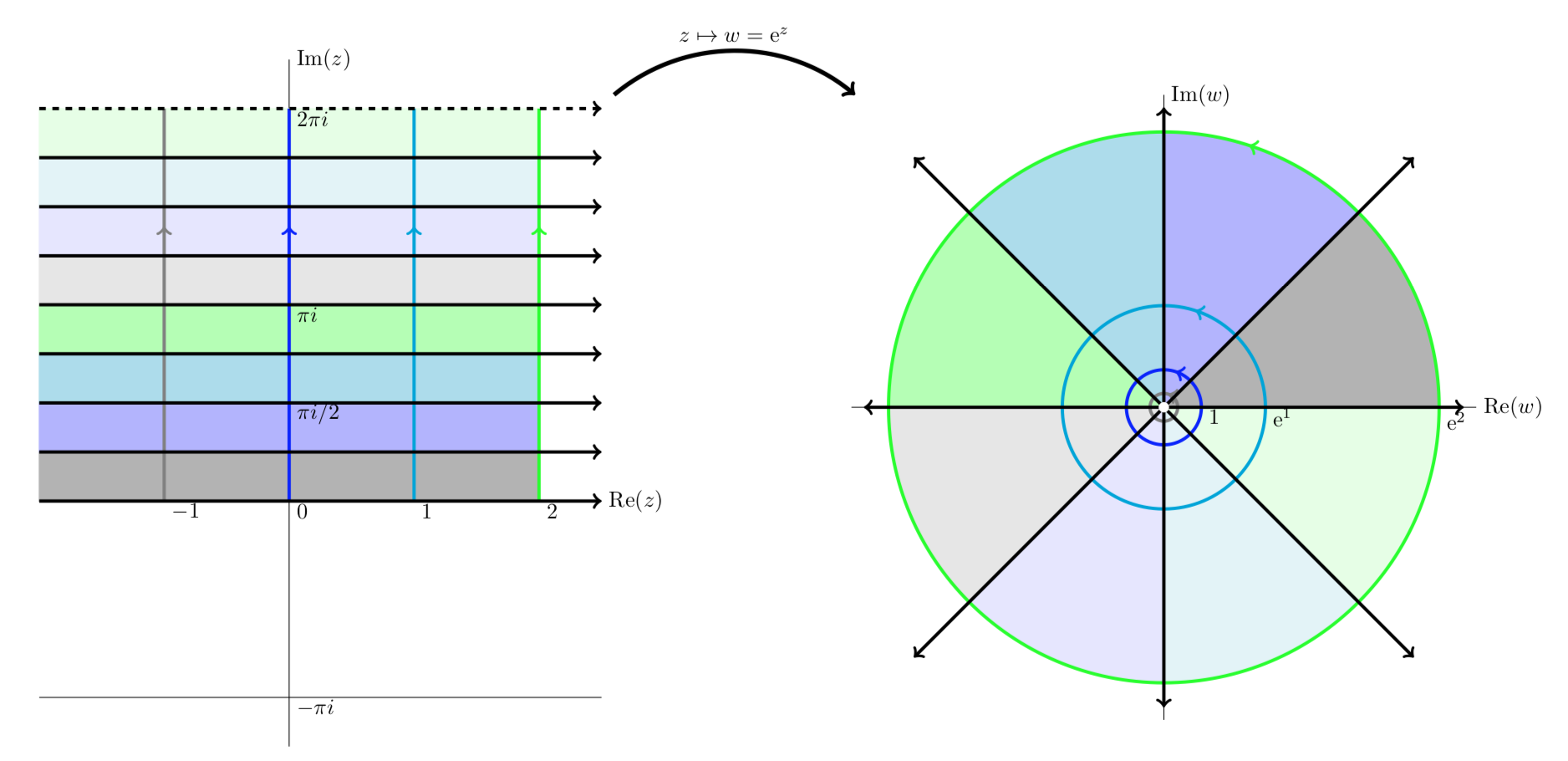
$2020-08-14 8.54.40.png$

La tira horizontal $0 \le y < 2\pi$ se mapea al plano perforado

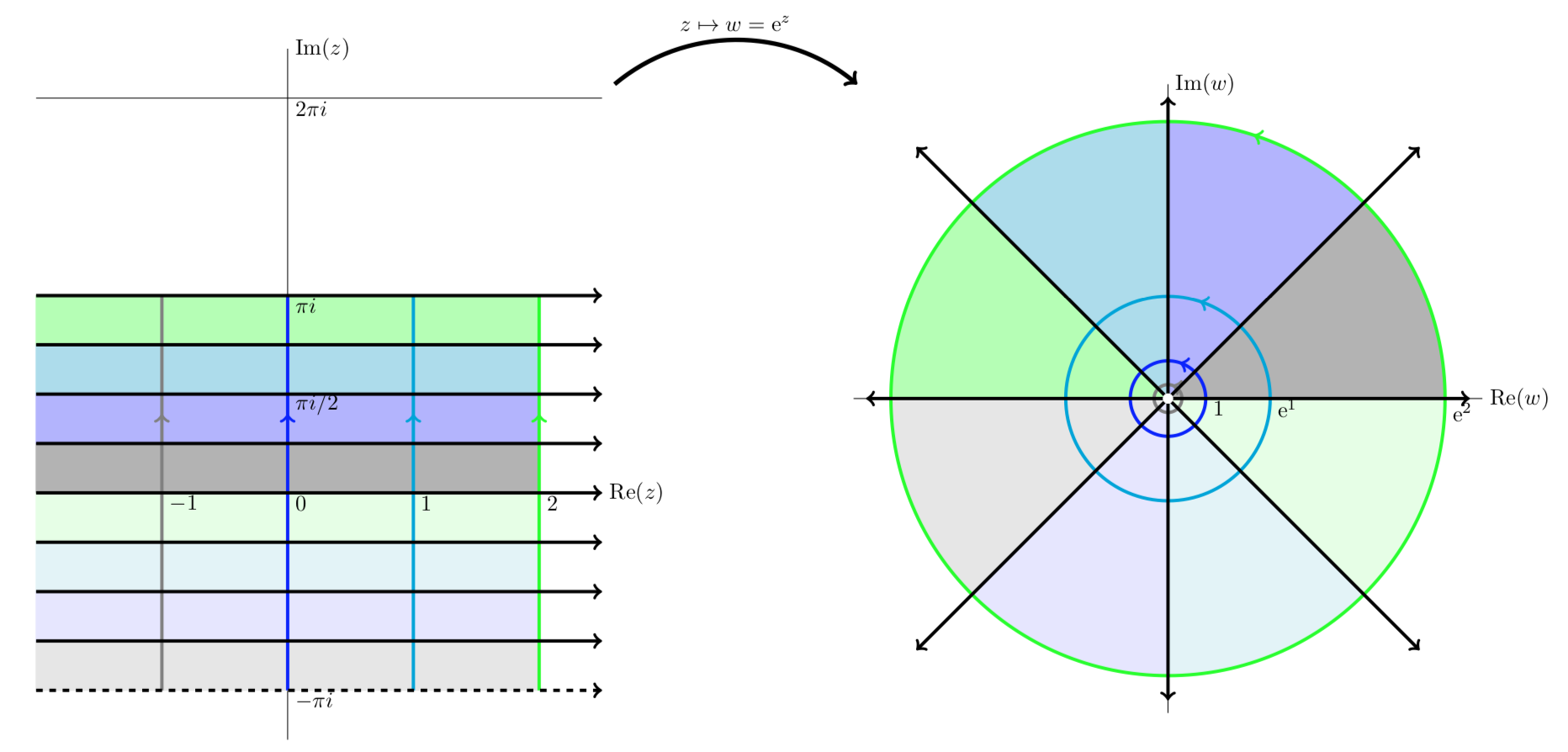
$2020-08-14 8.55.27.png$

La tira horizontal $-\pi < y \le \pi$ se mapea al plano perforado

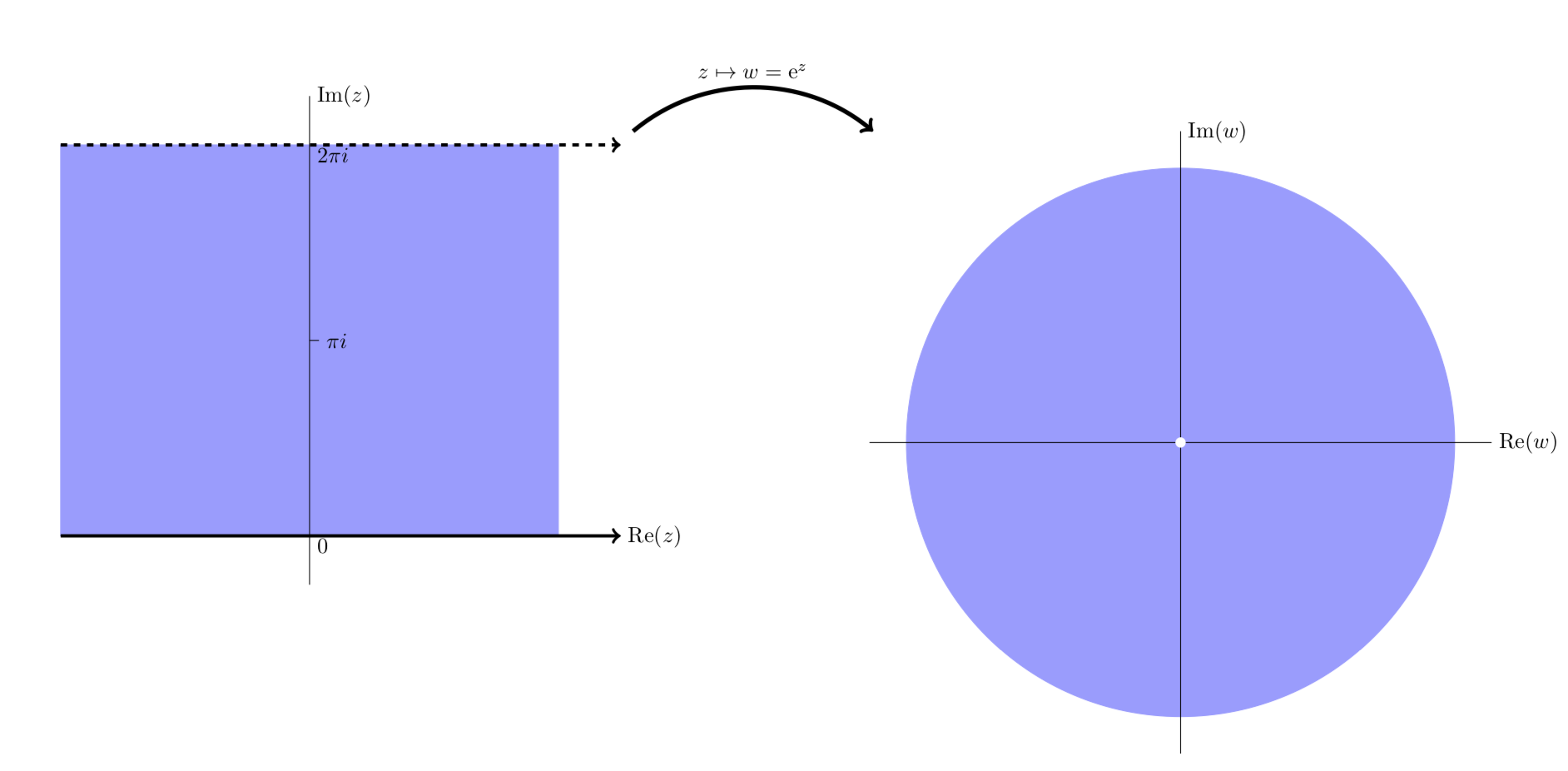
$2020-08-14 8.56.13.png$

Vista simplificada que muestra $e^z$ mapas de la franja horizontal $0 \le y < 2\pi$ al plano perforado.

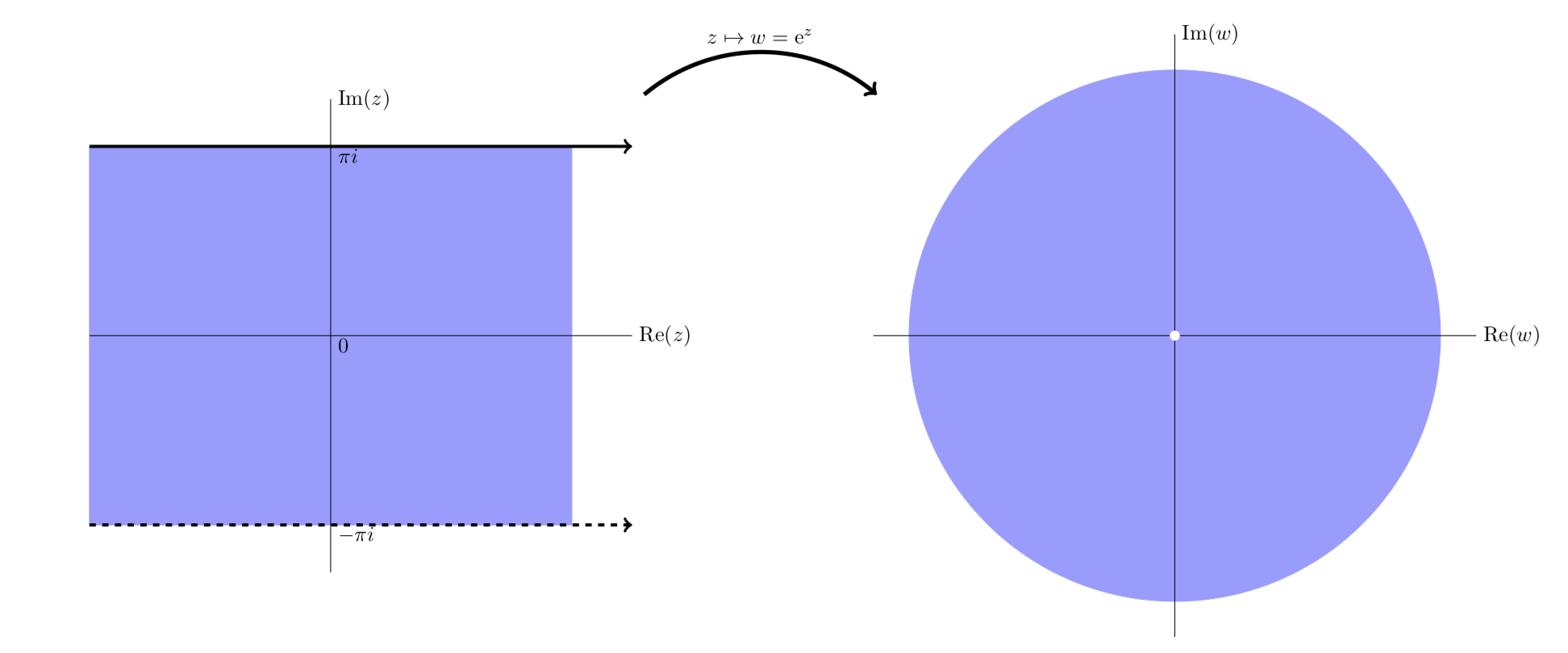
$2020-08-14 8.58.57.png$

Vista simplificada que muestra $e^z$ mapas de la franja horizontal $-\pi < y \le \pi$ al plano perforado.

Ejemplo1.8.1\PageIndex{1}

Ejemplo1.8.2\PageIndex{2}

Definición: plano perforado

Support Center

How can we help?

Ejemplo $\PageIndex{1}$

Ejemplo $\PageIndex{2}$