3.8: Extensiones y Aplicaciones del Teorema de Green
- Page ID
- 109838
Regiones Simply Connected
Una región\(D\) en el plano simplemente se conecta si no tiene “agujeros”. Dicho de otra manera, simplemente está conectado por cada simple curva cerrada\(C\) en\(D\), el interior de\(C\) está completamente contenido en\(D\).
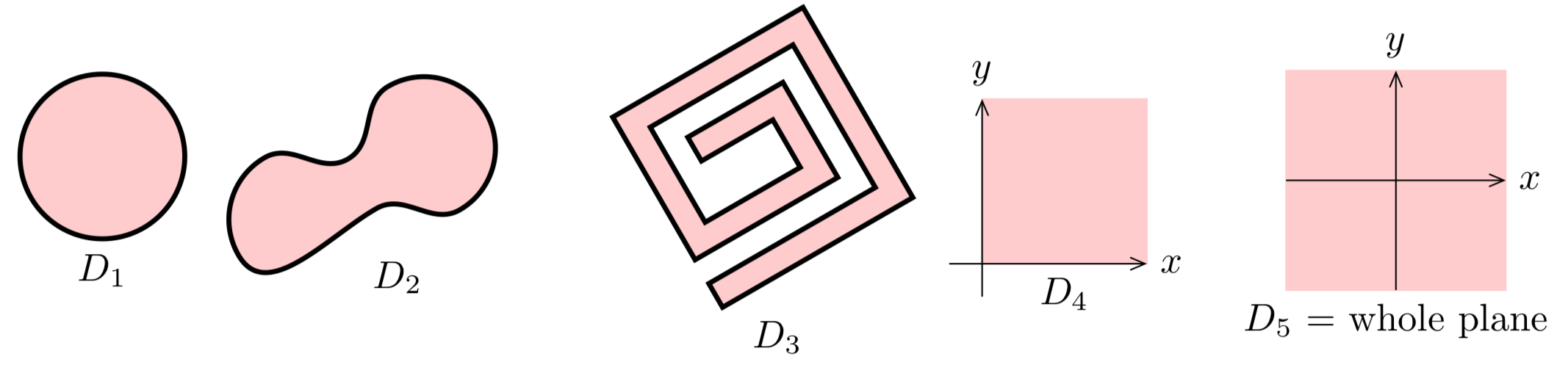
\(D_1\)- simplemente\(D_5\) están conectados. Para cualquier curva cerrada simple\(C\) dentro de cualquiera de estas regiones, el interior de\(C\) está completamente dentro de la región.
Nota: A veces decimos que cualquier curva se puede encoger hasta un punto sin salir de la región.
Las regiones de abajo no están simplemente conectadas. Para cada uno, el interior de la curva no\(C\) está del todo en la región.
Teorema del potencial
Aquí hay una aplicación del teorema de Green que nos dice cómo detectar un campo conservador en una región simplemente conectada. El teorema no tiene un nombre estándar, por lo que elegimos llamarlo Teorema Potencial.
Toma\(F = (M, N)\) definida y diferenciable en una región\(D\).
- Si\(F = \nabla f\) entonces\(\text{curl}F = N_x - M_y = 0\).
- Si simplemente\(D\) está conectado y\(\text{curl} F = 0\) encendido\(D\), entonces\(F = \nabla f\) para algunos\(f\).
Sabemos que en una región conectada, ser un campo degradado equivale a ser conservador. Entonces podemos reafirmar el Teorema del Potencial como: en una región simplemente conectada,\(F\) es conservador es equivalente a\(\text{curl} F = 0\).
- Prueba
-
Prueba de (a):\(F = (f_x, f_y)\), entonces\(\text{curl} F = f_{yx} - f_{xy} = 0\).
Prueba de (b): Supongamos que\(C\) es una simple curva cerrada en\(D\). Ya que simplemente\(D\) se conecta el interior de\(C\) está también en\(D\). Por lo tanto, usando el teorema de Green tenemos,
\[\oint_{C} F \cdot dr = \int \int_{R} \text{curl} F\ dA = 0.\]
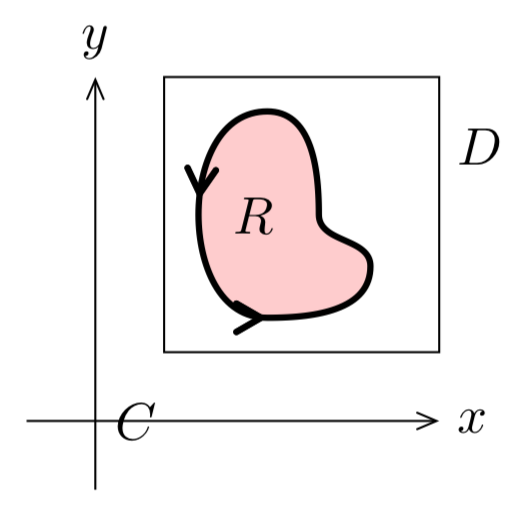
Figura\(\PageIndex{3}\): Teorema del potencial Esto demuestra que\(F\) es conservador en\(D\). Por lo tanto, se trata de un campo degradado.
Resumen: Supongamos que el campo vectorial\(F = (M, N)\) está definido en una región simplemente conectada\(D\). Entonces, las siguientes declaraciones son equivalentes.
- \(\int_P^Q F \cdot dr\)es independiente del camino.
- \(\oint_{C} F \cdot dr = 0\)para cualquier camino cerrado\(C\).
- \(F = \nabla f\)para algunos\(f\) en\(D\).
- \(F\)es conservador en\(D\).
Si\(F\) es continuamente diferenciable entonces 1, 2, 3, 4 todos implican 5: - \(\text{curl} F = N_x - M_y = 0\)en\(D\)
necesitan simplemente conectados en el Teorema del Potencial
Si hay un agujero entonces\(F\) podría no estar definido en el interior de\(C\). (Figura\(\PageIndex{4}\))
Teorema de Green Extended
Podemos extender el teorema de Green a una región\(R\) que tiene múltiples curvas de límite.
Supongamos que\(R\) es la región entre las dos curvas cerradas simples\(C_1\) y\(C_2\).
(\(R\)La nota siempre está a la izquierda a medida que recorre cualquiera de las curvas en la dirección indicada).
Entonces podemos extender el teorema de Green a esta configuración mediante
\[\oint_{C_1} F \cdot dr + \oint_{C_2} F \cdot dr = \int \int_R \text{curl} F \ dA.\]
Del mismo modo para más de dos curvas:
\[\oint_{C_1} F \cdot dr + \oint_{C_2} F \cdot dr + \oint_{C_3} F \cdot dr + \oint_{C_4} F \cdot dr = \int \int_R \text{curl} F \ dA.\]
\(Proof\). La prueba se basa en la siguiente figura. Nosotros 'cortamos' ambos\(C_1\)\(C_2\) y los conectamos por dos copias de\(C_3\), una en cada dirección. (En la figura hemos dibujado las dos copias de\(C_3\) como curvas separadas, en realidad son la misma curva atravesada en direcciones opuestas).
Ahora la curva\(C = C_1+ C_3 + C_2 - C_3\) es una simple curva cerrada y el teorema de Green se sostiene sobre ella. Pero la región interior\(C\) es exactamente\(R\) y las aportaciones de los dos ejemplares de\(C_3\) cancelan. Es decir, hemos demostrado que
\[\int \int_R \text{curl} F\ dA = \int_{C_1 + C_3 + C_2 - C_3} F \cdot dr = \int_{C_1 + C_2} F \cdot dr.\]
Este es exactamente el teorema de Green, que queríamos probar.
Let\(F = \dfrac{(-y, x)}{r^2}\) (“campo tangencial”)
\(F\)se define en\(D\) = plano - (0, 0) = el plano perforado (Figura\(\PageIndex{7}\)).
Es fácil de calcular (lo hemos hecho antes) que\(\text{curl}F = 0\) en\(D\).
Pregunta: Para el campo tangencial\(F\) ¿qué valores pueden\(\oint_{C} F \cdot dr\) tomar para\(C\) una simple curva cerrada (orientada positivamente)?
Solución
Tenemos dos casos (i)\(C_1\) no alrededor de 0 (ii)\(C_2\) alrededor de 0
En el caso (i) el teorema de Green se aplica porque el interior no contiene el punto problemático en el origen. Por lo tanto,
\[\oint_{C_1} F \cdot dr = \int\int_R \text{curl} F\ dA = 0.\]
Para el caso (ii) demostraremos que
dejar\(C_3\) ser un pequeño círculo de radio\(a\), completamente dentro\(C_2\). Por el teorema extendido de Green tenemos
\[\oint_{C_2} F \cdot dr - \oint_{C_3} F \cdot dr = \int\int_R \text{curl} F\ dA = 0.\]
Por lo tanto,\(\oint_{C_2} F \cdot dr = \oint_{C_3} F \cdot dr\).
Usando la parametrización habitual de un círculo podemos calcular fácilmente que la integral de línea es
\[\int_{C_3} F \cdot dr = \int_{0}^{2\pi} 1 \ dt = 2\pi. \ \ \ \ QED.\]
Respuesta a la pregunta: Los únicos valores posibles son 0 y\(2\pi\).
Podemos extender esta respuesta de la siguiente manera:
Si no\(C\) es sencillo, entonces los valores posibles de\(\oint_C F \cdot dr\) son\(2\pi n\), donde\(n\) está el número de veces que\(C\) va (en sentido antihorario) alrededor de (0,0).
No para clase:\(n\) se llama el número de bobinado de\(C\) alrededor de 0. \(n\)también es igual al número de veces que\(C\) cruza el\(x\) eje positivo, contando +1 desde abajo y -1 desde arriba.


