5.2: Fórmula Integral de Cauchy para Derivados
- Page ID
- 109842
Vale la pena repetir varias veces la fórmula integral de Cauchy. Entonces, ahora lo damos por todos los derivados\(f^{(n)} (z)\) de\(f\). Esto incluirá la fórmula para funciones como caso especial.
Si\(f(z)\) y\(C\) satisfacer las mismas hipótesis que para la fórmula integral de Cauchy entonces, para todos\(z\) dentro\(C\) tenemos
\[f^{(n)} (z) = \dfrac{n!}{2 \pi i } \int_C \dfrac{f(w)}{(w - z)^{n + 1}} \ dw, \ \ n = 0, 1, 2, ...\]
donde,\(C\) es una curva cerrada simple, orientada en sentido antihorario,\(z\) está dentro\(C\) y\(f(w)\) es analítica por dentro y por dentro\(C\).
Evaluar\(I = \int_C \dfrac{e^{2z}}{z^4} \ dz\) dónde\(C : |z| = 1\).
Solución
Con la fórmula de Cauchy para derivados esto es fácil. Vamos\(f(z) = e^{2z}\). Entonces,
\[I = \int_C \dfrac{f(z)}{z^4} \ dz = \dfrac{2 \pi i} {3!} f''' (0) = \dfrac{8}{3} \pi i.\]
Ahora dejemos\(C\) ser el contorno que se muestra a continuación y evalúe la misma integral que en el ejemplo anterior.
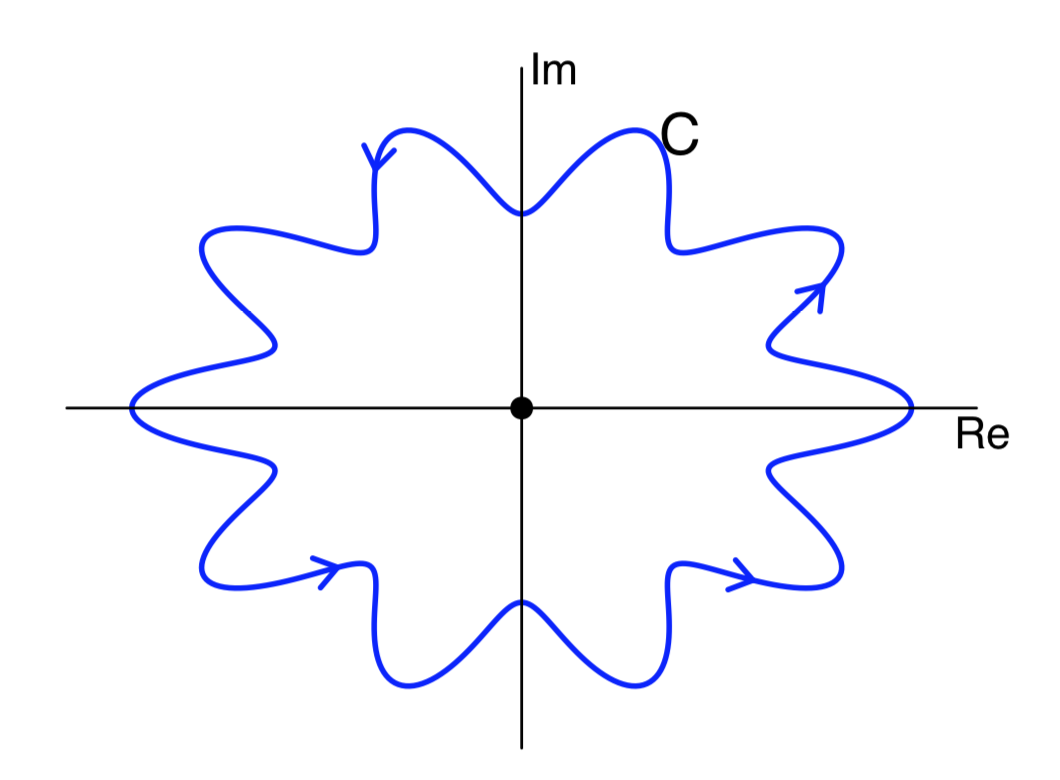
Solución
Nuevamente esto es fácil: la integral es la misma que el ejemplo anterior, es decir\(I = \dfrac{8}{3} \pi i\).
Otra aproximación a algunos ejemplos básicos
Supongamos que\(C\) es una simple curva cerrada alrededor de 0. Hemos visto que
\[\int_{C} \dfrac{1}{z} \ dz = 2 \pi i.\]
La fórmula integral de Cauchy da el mismo resultado. Es decir, vamos\(f(z) = 1\), entonces la fórmula dice
\[\dfrac{1}{2\pi i} \int_{C} \dfrac{f(z)}{z - 0}\ dz = f(0) = 1.\]
Asimismo, la fórmula de Cauchy para derivados muestra
\[\int_{C} \dfrac{1}{(z)^n}\ dz = \int_{C} \dfrac{f(z)}{z^{n + 1}} \ dz = f^{(n)} (0) = 0, \text{ for integers } n > 1.\]
Más ejemplos
Calcular\(\int_C \dfrac{\cos (z)}{z(z^2 + 0)} \ dz\) sobre el contorno mostrado.
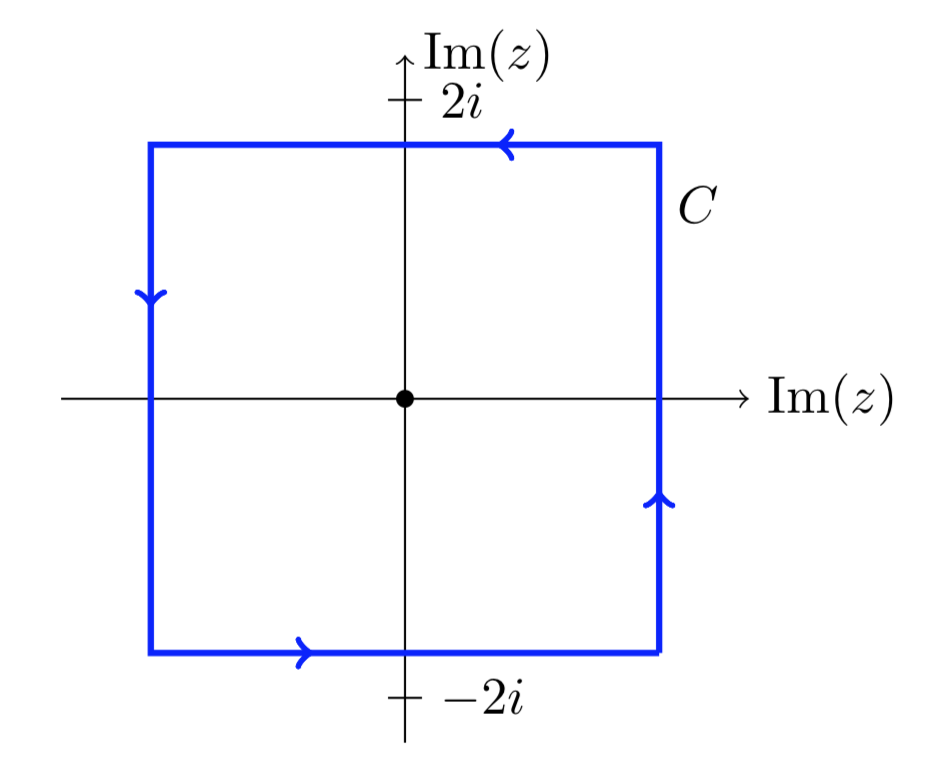
Solución
Vamos\(f(z) = \cos (z)/ (z^2 + 8)\). \(f(z)\)es analítico dentro y dentro de la curva\(C\). Es decir, las raíces de\(z^2 + 8\) están fuera de la curva. Entonces, reescribimos la integral como
\[\int_C \dfrac{\cos (z)/ (z^2 + 8)}{z} \ dz = \int_C \dfrac{f(z)}{z} \ dz = 2 \pi i f(0) = 2 \pi i \dfrac{1}{8} = \dfrac{\pi i}{4}.\]
Calcular\(\int_C \dfrac{1}{(z^2 + 4)^2}\ dz\) sobre el contorno mostrado.
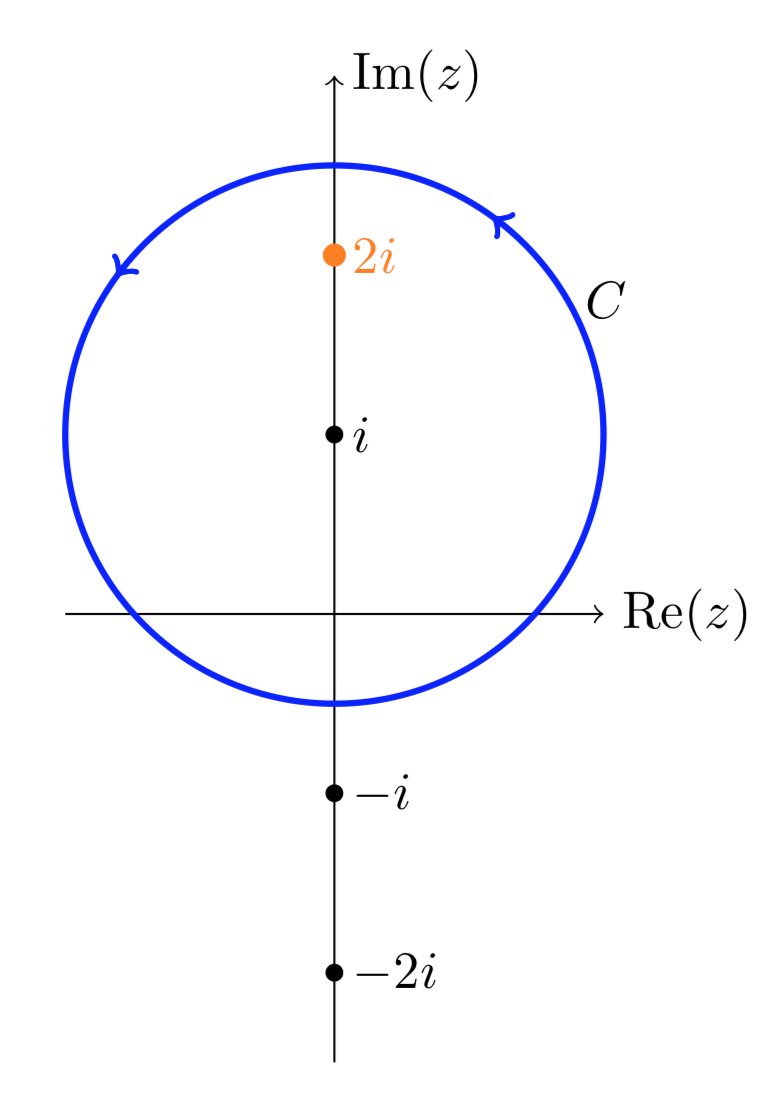
Solución
Facturamos el denominador como
\[\dfrac{1}{(z^2 + 4)^2} = \dfrac{1}{(z - 2i)^2 (z + 2i)^2}.\]
Let
\[f(z) = \dfrac{1}{(z + 2i)^2}.\]
Claro\(f(z)\) es analítico por dentro\(C\). Entonces, por la fórmula de Cauchy para derivados:
\[\int_C \dfrac{1}{(z^2 + 4)^2} \ dz = \int_C \dfrac{f(z)}{(z - 2i)^2} = 2 \pi i f'(2i) = 2\pi i [\dfrac{-2}{(z + 2i)^3}]_{z = 2i} = \dfrac{4 \pi i}{64 i} = \dfrac{\pi}{16}\]
Calcula\(\int_C \dfrac{z}{z^2 + 4} \ dz\) sobre la curva que\(C\) se muestra a continuación.
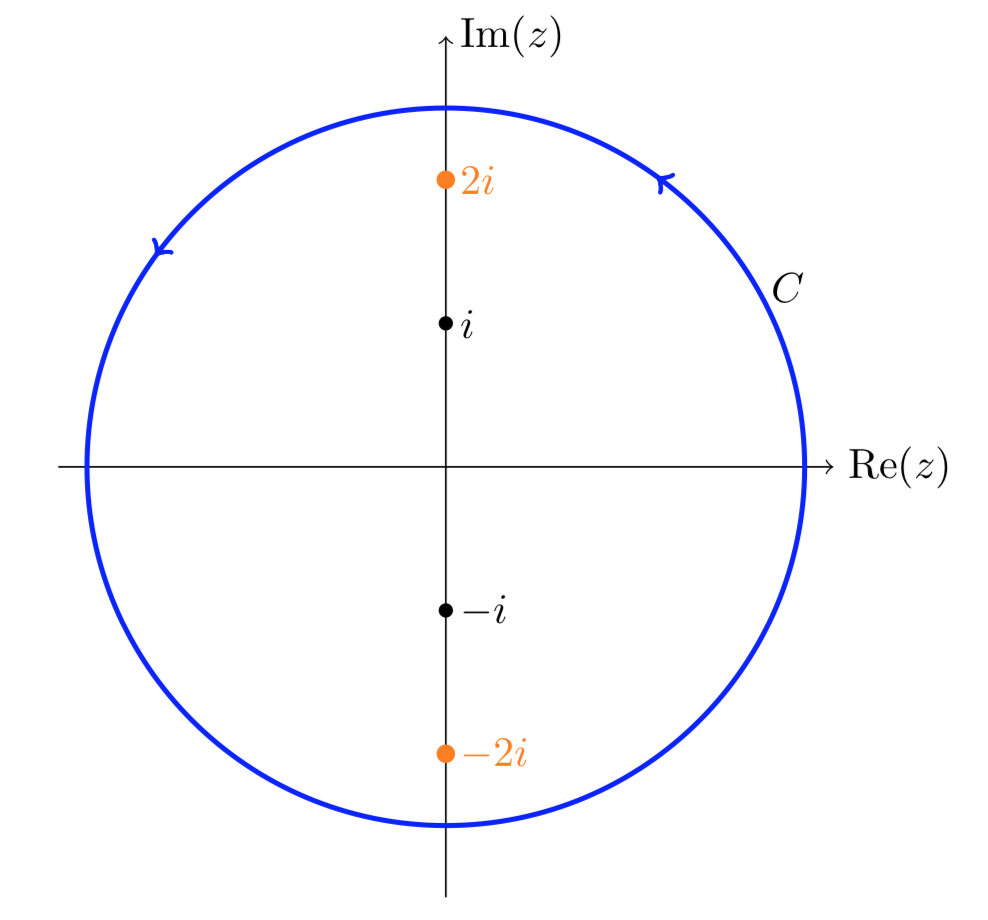
Solución
El integrando tiene singularidades en\(\pm 2i\) y la curva las\(C\) encierra a ambas. La solución a la solución anterior no va a funcionar porque no podemos encontrar una adecuada\(f(z)\) que sea analítica en todo el interior de\(C\). Nuestra solución es dividir la curva en dos partes. Observe que\(C_3\) se recorre tanto hacia adelante como hacia atrás.
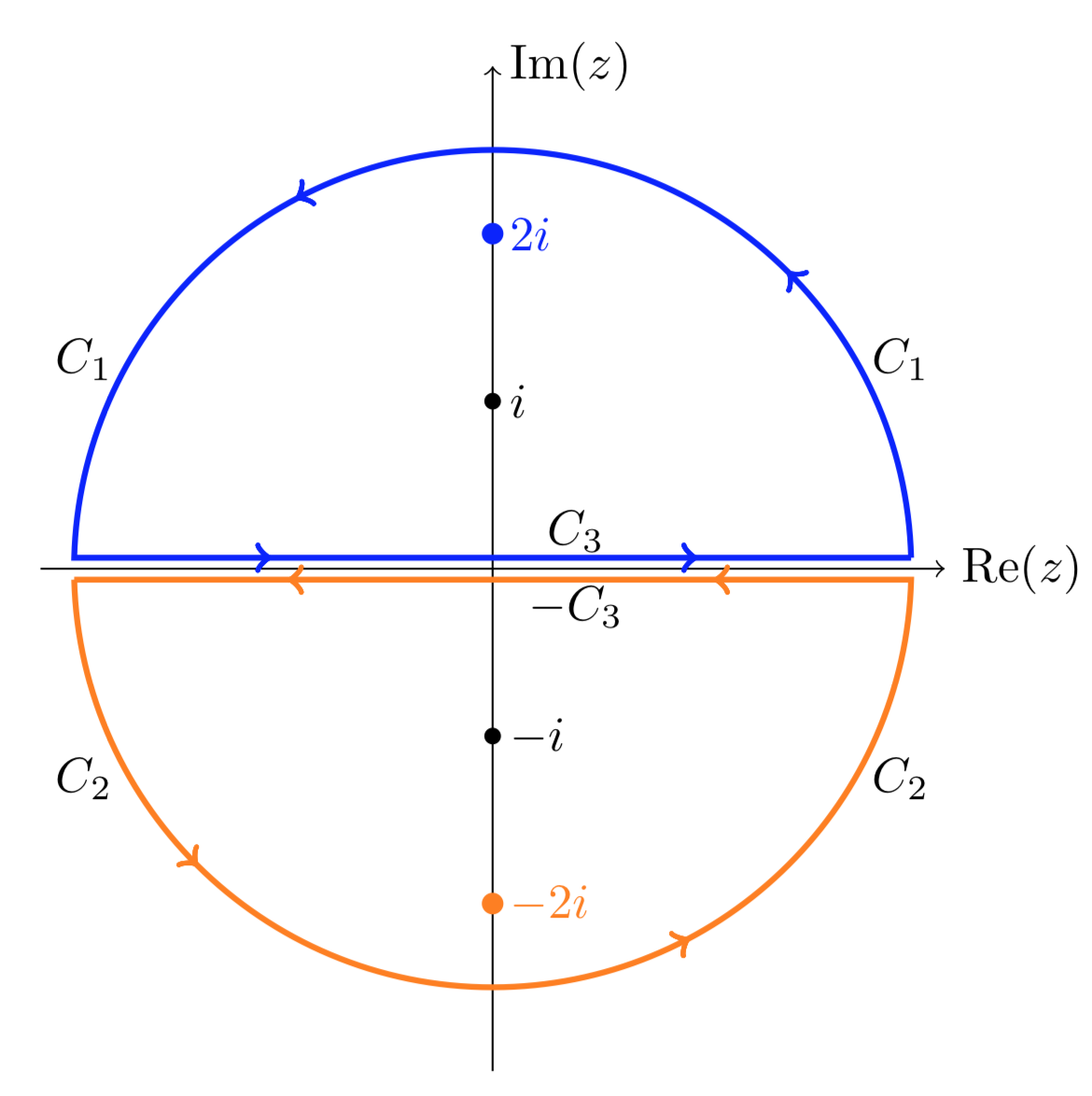
Divide la curva original\(C\) en 2 piezas que rodean cada una solo una singularidad.
Tenemos
\[\dfrac{z}{z^2 + 4} = \dfrac{z}{(z - 2i)(z + 2i)}.\]
Dejamos
\[f_1 (z) = \dfrac{z}{z + 2i} \text{ and } f_2 (z) = \dfrac{z}{z - 2i}.\]
Entonces,
\[\dfrac{z}{z^2 + 4} = \dfrac{f_1(z)}{z - 2i} = \dfrac{f_2(z)}{z + 2i}.\]
La integral, puede escribirse como
\[\int_{C} \dfrac{z}{z^2 + 4} \ dz = \int_{C_1 + C_3 - C_3 + C_2} \dfrac{z}{z^2 + 4} \ dz = \int_{C_1 + C_3} \dfrac{f_1 (z)}{z - 2i} \ dz + \int_{C_2 - C_3} \dfrac{f_2 (z)}{z + 2i} \ dz\]
Dado que\(f_1\) es analítico dentro de la curva cerrada simple\(C_1 + C_3\) y\(f_2\) es analítico dentro de la curva cerrada simple\(C_2 - C_3\), la fórmula de Cauchy se aplica a ambas integrales. La integral total es igual a
\[2\pi i (f_1(2i) + f_2 (-2i)) = 2\pi i (1/2 + 1/2) = 2\pi i.\]
Observaciones. 1. También podríamos haber hecho este problema usando fracciones parciales:
\[\dfrac{z}{(z - 2i) (z + 2i)} = \dfrac{A}{z - 2i} + \dfrac{B}{z + 2i}.\]
Va a resultar que\(A = f_1 (2i)\) y\(B = f_2(-2i)\). Es fácil aplicar la fórmula integral de Cauchy a ambos términos.
2. Nota importante. En un tema próximo formularemos el teorema del residuo de Cauchy. Esto nos permitirá calcular las integrales en los Ejemplos 5.3.3-5.3.5 de una manera más fácil y menos ad hoc.
desigualdad triangular para integrales
Se discutió la desigualdad triangular en las notas del Tema 1. Dice que
\[|z_1 + z_2| \le |z_1| + |z_2|,\]
con igualdad si y sólo si\(z_1\) y\(z_2\) se encuentran sobre el mismo rayo desde el origen.
Una variante útil de esta afirmación es
\[|z_1| - |z_2| \le |z_1 - z_2|.\]
Esto sigue porque la Ecuación 5.3.17 implica
\[|z_1| = |(z_1 - z_2) + z_2| \le |z_1 - z_2| + |z_2|.\]
Ahora sustrayendo\(z_2\) de ambos lados da la Ecuación 5.3.18
Dado que una integral es básicamente una suma, esto se traduce en la desigualdad triangular para integrales. Lo declararemos de dos maneras que nos serán útiles.
Supongamos que\(g(t)\) es una función valorada compleja de una variable real, definida en\(a \le t \le b\). Entonces
\[|\int_{a}^{b} g(t) \ dt| \le \int_{a}^{b} |g(t)|\ dt,\]
con igualdad si y sólo si los valores de\(g(t)\) todos se encuentran en el mismo rayo desde el origen.
- Prueba
-
Esto sigue aproximando la integral como una suma de Riemann.
\[|\int_{a}^{b} g(t)\ dt| \approx |\sum g(t_k) \Delta t| \le \sum |g(t_k)| \Delta t \approx \int_{a}^{b} |g(t)|\ dt.\]
La desigualdad media es solo la desigualdad triangular estándar para sumas de números complejos.
Para cualquier función\(f(z)\) y cualquier curva\(\gamma\), tenemos
\[|\int_{\gamma} f(z)\ dz| \le \int_{\gamma} |f(z)|\ |dz|.\]
Aquí\(dz = \gamma ' (t)\ dt\) y\(|dz| = |\gamma ' (t)|\ dt\).
- Prueba
-
Esto se desprende inmediatamente del teorema anterior:
\[|\int_{\gamma} f(z)\ dz| = |\int_{a}^{b} f(\gamma (t)) \gamma ' (t)\ dt| \le \int_{a}^{b} |f(\gamma (t))|\ |\gamma ' (t)| \ dt = \int_{\gamma} |f(z)|\ |dz|.\]
Si\(|f(z)| < M\) en\(C\) entonces
\[|\int_C f(z)\ dz| \le M \cdot \text{(length of } C).\]
- Prueba
-
Dejemos\(\gamma (t)\), con\(a \le t \le b\), ser una parametrización de\(C\). Usando la desigualdad del triángulo
\[|\int_C f(z)\ dz| \le \int_C |f(z)|\ |dz| = \int_{a}^{b} |f(\gamma (t))|\ |\gamma '(t)|\ dt \le \int_{a}^{b} M|\gamma ' (t)|\ dt = M \cdot \text{(length of } C).\]
Aquí hemos usado eso
\[|\gamma ' (t)|\ dt = \sqrt{(x')^2 + (y')^2} \ dt = ds,\]
el elemento arclongitud.
Calcular la integral real
\[I = \int_{-\infty}^{\infty} \dfrac{1}{(x^2 + 1)^2}\ dx\]
Solución
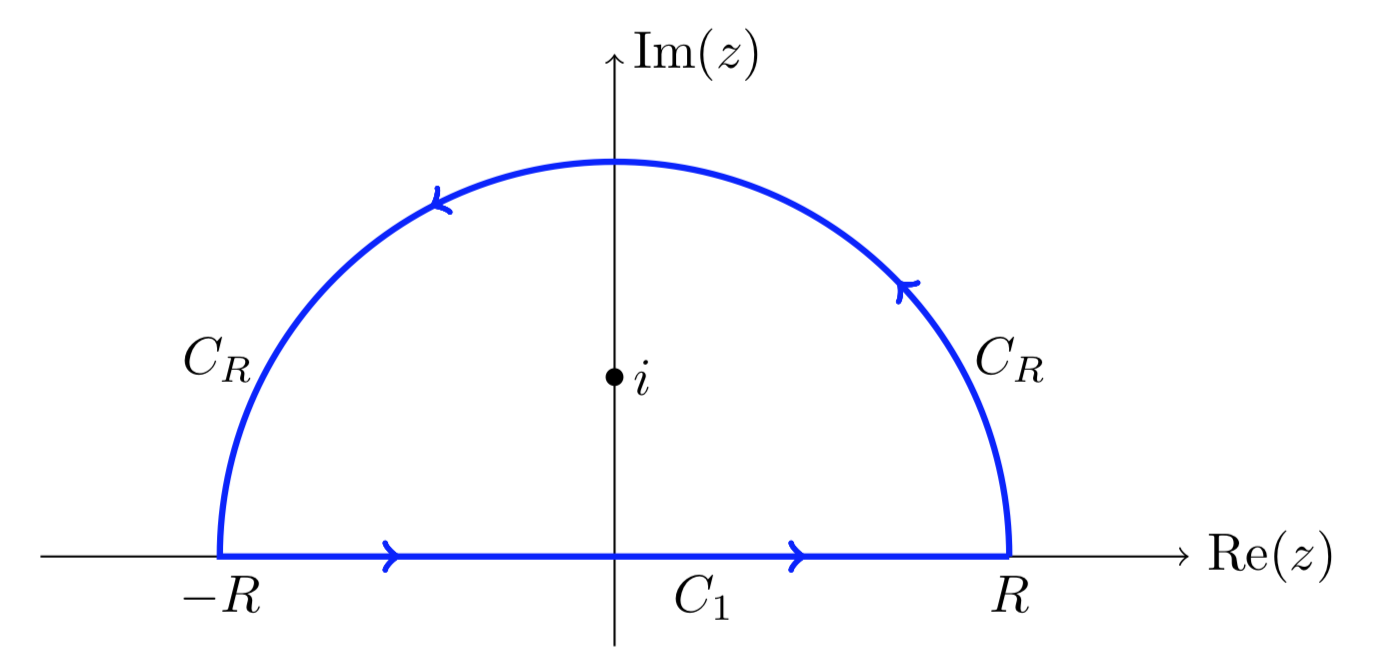
El truco es integrarse\(f(z) = 1/(z^2 + 1)^2\) sobre el contorno cerrado que\(C_1 + C_R\) se muestra, para luego mostrar que el aporte de\(C_R\) a esta integral se desvanece como\(R\) va a\(\infty\).
La única singularidad de
\[f(z) = \dfrac{1}{(z + i)^2 (z - i)^2}\]
dentro del contorno está en\(z = i\). Let
\[g(z) = \dfrac{1}{(z + i)^2}.\]
Dado que\(g\) es analítico dentro y dentro del contorno, la fórmula de Cauchy da
\[\int_{C_1 + C_R} f(z)\ dz = \int_{C_1 + C_R} \dfrac{g(z)}{(z - i)^2}\ dz = 2\pi i g'(i) = 2\pi i \dfrac{-2}{(2i)^3} = \dfrac{\pi}{2}.\]
Parametrizamos\(C_1\) por
\[\gamma (x) = x, \text{ with } -R \le x \le R.\]
Entonces,
\[\int_{C_1} f(z)\ dz = \int_{-R}^{R} \dfrac{1}{(x^2 + 1)^2}\ dx.\]
Esto va a\(I\) (el valor que queremos calcular) como\(R \to \infty\).
A continuación, parametrizamos\(C_R\) por
\[\gamma (\theta) = R e^{i \theta}, \text{ with } 0 \le \theta \le \pi.\]
Entonces,
\[\int_{C_R} f(z) \ dz = \int_{0}^{\pi} \dfrac{1}{(R^2 e^{2i \theta} + 1)^2} i Re^{i \theta} \ d \theta\]
Por el triángulo desigualdad para integrales, si\(R > 1\)
\[|\int_{C_R} f(z)\ dz| \le \int_{0}^{\pi} |\dfrac{1}{(R^2 e^{2i \theta} + 1)^2} iRe^{i \theta}|\ d\theta.\]
Del triángulo igualdad en la forma Ecuación 5.3.18 sabemos que
\[|R^2 e^{2i \theta} + 1| \ge |R^2 e^{2i \theta}| - |1| = R^2 - 1.\]
Por lo tanto,
\[\dfrac{1}{|R^2 e^{2i \theta} + 1|} \le \dfrac{1}{R^2 - 1} \ \ \Rightarrow \ \ \dfrac{1}{|R^2 e^{2i \theta} + 1|^2} \le \dfrac{1}{(R^2 - 1)^2}.\]
Usando la Ecuación 5.3.34, entonces tenemos
\[|\int_{C_R} f(z) \ dz| \le \int_{0}^{\pi} |\dfrac{1}{(R^2 e^{2i \theta} + 1)^2} iRe^{i \theta}|\ d\theta \le \int_{0}^{\pi} \dfrac{R}{(R^2 - 1)^2}\ d\theta = \dfrac{1}{(R^2 - 1)^2}.\]
Claramente esto va a 0 como\(R\) va al infinito. Así, la integral sobre el contorno\(C_1 + C_R\) va a\(I\) como\(R\) se agranda. Pero
\[\int_{C_1 + C_R} f(z) \ dz = \pi /2\]
para todos\(R > 1\). Por lo tanto, podemos concluir eso\(I = \pi /2\).
Como control de cordura, observamos que nuestra respuesta es real y positiva como debe ser.


